[电路分析]替代定理

替代定理适用范围嘿，朋友们！咱们今天来聊聊替代定理的适用范围。

先说说啥是替代定理吧。

就好比你有一辆旧自行车，某个零件坏了，你要是能找到一个完全能替代它的新零件，而且这新零件装上后自行车照样跑得顺溜，这就是一种替代。

那在电路里呢，替代定理说的是，如果一个二端网络端口的电压和电流是确定的，那我们就可以用一个电压源或者电流源来替代它，而且电路里其他部分的情况不会受到影响。

那它到底能在哪些地方大展身手呢？比如说在复杂的电路分析中，一堆电阻、电容、电感缠在一起，像一团乱麻。

这时候，如果能找到符合条件的部分，用上替代定理，那不就像是在乱麻里找到了一根能抽出来的线头，一下子让整个局面清晰起来了吗？再想象一下，一个大工厂的电路系统，要进行升级改造。

如果能准确运用替代定理，是不是就像在茫茫大海中找到了指明方向的灯塔，能让工程师们更轻松地搞定电路优化的工作？但可别以为替代定理是万能的哟！它也有自己的“小脾气”。

比如说，如果被替代的部分包含了受控源，那可就得小心了，这就好像你想给一只调皮的猴子找个替身，可没那么容易搞定。

还有啊，如果替代后的电路出现了不满足电路基本定律的情况，那也是不行的。

这就好比你想给一个房子换个新屋顶，结果新屋顶不符合建筑规范，那不是给自己找麻烦嘛！所以呢，在使用替代定理的时候，咱们得像走钢丝的杂技演员一样，小心翼翼，看准了再行动。

得把电路里的各种情况都摸清楚，不能马虎大意。

总之，替代定理就像是一把神奇的钥匙，但要用对地方才能打开电路分析的大门。

咱们可得把它的适用范围牢记在心，这样在面对复杂电路的时候，才能运用自如，让电路问题迎刃而解！。

电路替代定理
1.定义: 在有唯一解的电路中，其中第k支路的电压uk和电流ik 为已知，那么此支路就可以用大小和方向与uk相同的电压源替代，或用大小和方向与ik相同的电流源替代，替代后电路中全部电压和电流均将保持原值。

电路无论是线性还是非线性的，替代定理都成立。

N：第k支路外的电路其余部分。

第k支路：可以是无源的（电阻）、也可以是无源的（电压源和电阻的串联组合或电流源和电阻的并联组合）。

假如第k支路中的电压或电流为N中受控源的掌握量，而替代后该电压或电流不复存在，则该支路不能被替代。

2.替代定理的证明
（1）用电压源替代证明
a、b为自然等位点，短路后不影响其余电路的数值。

（2）用电流源替代证明
（3）规律证明
替代前后KCL，KVL关系相同，其余支路的u、i关系不变。

①用uk替代后，其余支路电压不变（KVL），其余支路电流也不变，故第k条支路ik也不变（KCL）。

②用ik替代后，其余支路电流不变（KCL），其余支路电压不变，故第k条支路uk也不变（KVL）。

3.特殊说明
（1）替代定理适用于线性和非线性电路。

（2）替代定理的应用必需满意的条件:
①替代后电路必需有唯一解
②替代后其余支路及参数不能转变(一点等效)。

（2）再用叠加定理：
例13. 试求图示电路在I = 2A时，20V电压源发出的功率。

例14. 图(a)电路中g = 2S。

试求电流I。

解：先用分压公式求受控源掌握变量U
用电流为gU=12A的电流源替代受控电流源，得到图(b)电路，该电路不含受控电源，可以用叠加定理求得电流为。

等效变换和替代定理等效变换是指在不改变电路特性的情况下，通过改变电路中元件的参数或者改变元件的位置，使得电路的形式发生变化，但是电路的特性不变。

等效变换是电路分析中常用的一种方法，可以简化电路分析的过程，提高电路分析的效率。

替代定理是指在电路中，任何两个电阻或电源可以互相替代，只要它们的电压和电流关系相同。

替代定理是电路分析中常用的一种方法，可以简化电路分析的过程，提高电路分析的效率。

下面分别对等效变换和替代定理进行详细介绍：一、等效变换1. 电阻的串并联变换在电路中，若有多个电阻串联或并联，可以通过串并联变换将它们简化为一个等效电阻。

串并联变换的原理是根据欧姆定律和基尔霍夫定律，将多个电阻串联或并联的电路转化为一个等效电阻的电路。

2. 电压源和电流源的等效变换在电路中，若有多个电压源或电流源，可以通过等效变换将它们简化为一个等效电源。

电压源和电流源的等效变换的原理是根据基尔霍夫定律和欧姆定律，将多个电压源或电流源的电路转化为一个等效电源的电路。

3. 电阻的星三角变换在电路中，若有多个电阻星型连接或三角形连接，可以通过星三角变换将它们简化为一个等效电阻。

星三角变换的原理是根据欧姆定律和基尔霍夫定律，将多个电阻星型连接或三角形连接的电路转化为一个等效电阻的电路。

二、替代定理1. 电阻的替代定理在电路中，任何两个电阻可以互相替代，只要它们的电压和电流关系相同。

电阻的替代定理可以简化电路分析的过程，提高电路分析的效率。

2. 电源的替代定理在电路中，任何两个电源可以互相替代，只要它们的电压和电流关系相同。

电源的替代定理可以简化电路分析的过程，提高电路分析的效率。

总之，等效变换和替代定理是电路分析中常用的两种方法，它们可以简化电路分析的过程，提高电路分析的效率。

在实际应用中，需要根据具体情况选择合适的方法进行电路分析。

《大学电路/电路原理/电路分析》06--替代定理的妙用电学中重要的电路定理有叠加定理、齐性定理、替代定理、戴维宁定理、诺顿定理和最大功率传输定理，在不同的场合解决各类电路问题，真的是太精妙了。

叠加定理把多电源电路变为单电源电路，一下子回到高中物理。

齐性定理体现了线性电路的比例性质，其“倒推法”用在单电源多电阻电路就是一个字--“绝”。

戴维宁定理和诺顿定理特别擅长于只求某一支路参数的场合，把待求支路从电路中一取走，变成开口电路，难度一下降低。

最大功率传输定理将复杂的求导变成求戴维宁/诺顿等效电路中的等效电阻了。

但唯独对替代定理的介绍最少，相应的例题应就更少。

其实替代定理是一个非常棒的定理，用得好，考试时大可以提前交卷！接下来介绍替代定理在推导及计算中的妙用。

1．替代定理替代定理是指已知电路中某一支路的参数，如两端的电压，流过支路的电流，那么该支路可等效为一个电压源，或电流源，又或是一个电阻，如下图所示：其证明过程也是相对简单的，等效为电压源时只需在支路上串联2个大小相等，方向相反的电压源，如下图所示：虚线框内支路电压刚好和下面的电压源抵消了，电压为0，可用一条导线替代，这样就只剩下面那个电压源了，得证。

而等效为电流源时，则需在支路两端并联2个大小相等，方向相反的电流源，如下图所示：虚线框内流过支路的电流和右边的电流源也抵消，电流为0，整个框可以去掉，只剩左边那个电流源了。

2. 替代定理在定理推导中的应用戴维宁定理是指，一个含源一端口可以等效为一个实际电压源模型，在证明时该定理就先替代定理，再用叠加定理来操作的，如下图所示：图中N s表示含源一端口，N0表示无源一端口。

有学生问替代时为什么选电流源而不选电压源，主要是由于在接着使用的叠加定理，将电流源置零时可直接将其断开，方便计算，如果选电压源，置零时就要短接，求解麻烦。

将分电路中求出的电压u叠加，得到表达式为：根据式中的电压电流关系，得到等效电路就是实际电压源模型，即戴维宁等效电路，如下图所示：看到这里，只想喊一句：“太妙了！”3．替代定理在解题中的应用替代定理在一些复杂电路中最能显示它的优势，如下图所示：电路要求电流I1，但电路结构很复杂，支路多，电源、电阻也多，看到都头晕。

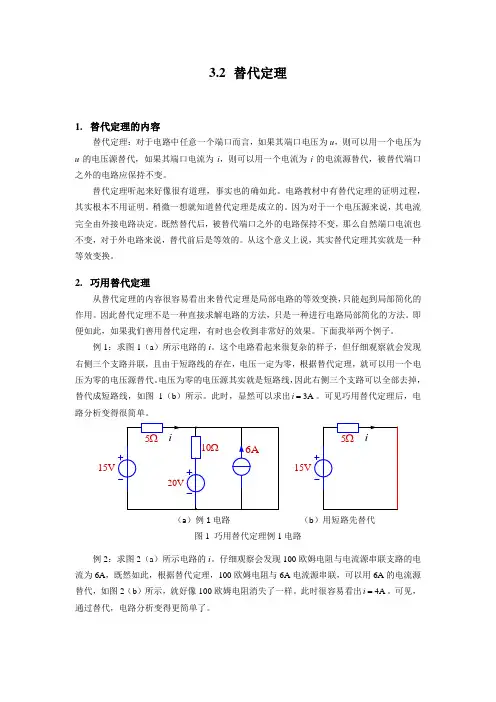
3.2 替代定理1. 替代定理的内容替代定理：对于电路中任意一个端口而言，如果其端口电压为u ，则可以用一个电压为u 的电压源替代，如果其端口电流为i ，则可以用一个电流为i 的电流源替代，被替代端口之外的电路应保持不变。

替代定理听起来好像很有道理，事实也的确如此。

电路教材中有替代定理的证明过程，其实根本不用证明。

稍微一想就知道替代定理是成立的。

因为对于一个电压源来说，其电流完全由外接电路决定。

既然替代后，被替代端口之外的电路保持不变，那么自然端口电流也不变，对于外电路来说，替代前后是等效的。

从这个意义上说，其实替代定理其实就是一种等效变换。

2. 巧用替代定理从替代定理的内容很容易看出来替代定理是局部电路的等效变换，只能起到局部简化的作用。

因此替代定理不是一种直接求解电路的方法，只是一种进行电路局部简化的方法。

即便如此，如果我们善用替代定理，有时也会收到非常好的效果。

下面我举两个例子。

例1：求图1（a ）所示电路的i 。

这个电路看起来很复杂的样子，但仔细观察就会发现右侧三个支路并联，且由于短路线的存在，电压一定为零，根据替代定理，就可以用一个电压为零的电压源替代。

电压为零的电压源其实就是短路线，因此右侧三个支路可以全部去掉，替代成短路线，如图1（b ）所示。

此时，显然可以求出3A i =。

可见巧用替代定理后，电路分析变得很简单。

15V15V （a ）例1电路 （b ）用短路先替代图1 巧用替代定理例1电路例2：求图2（a ）所示电路的i 。

仔细观察会发现100欧姆电阻与电流源串联支路的电流为6A ，既然如此，根据替代定理，100欧姆电阻与6A 电流源串联，可以用6A 的电流源替代，如图2（b ）所示，就好像100欧姆电阻消失了一样。

此时很容易看出4A i =。

可见，通过替代，电路分析变得更简单了。

（a）例2电路（b）用电流源替代图2 巧用替代定理例2的电路3.问与答问：替代定理看起来与等效变换很像，它们之间有何异同？答：替代定理与等效变换的关系很难说得清楚。

中国大学M O O C中国大学M OO C中国大学M O OC中国大学M O OC中国大学MO O C中国大学M O O Cku _+Su _+Nki Si NkR N在线性和非线性电路中，若第k 条支路的电压u k 和电流i k 已知，则该支路可用下列任一元件组成的支路替代:（1）电压为u k 的理想电压源；（2）电流为i k 的理想电流源；（3）电阻为R k =u k /i k 的电阻元件。

替代前后，电路响应不变。

k路支_+N（1）（2）（3）或或学MOO C 中国大学MOO C中国大学MO OC 学MOOC中国大学MOOC中国大学M OO C学MOOC中国大学MOOC中国大学MO OC学MOOC中国大学MOOC中国大学MO OC学MOO C 中国大学MOOC中国大学MO OC学MOOC中国大学MOO C 中国大学M O O Cki ku替代前后KCL 、KVL 关系（方程）相同，其余支路的元件（u 、i 关系）不变。

用u S 替代后，第k 条支路u k 不变，其余支路电压、支路电流不变；用i S 替代后，第k 条支路i K 不变；用R k 替代后，第k 条支路支路电流、电压关系不变。

原因⎧⎪⎪⎨⎪⎪⎩（n-1)个KCL 方程[b-(n-1)]个KVL 方程(b-1)个元件方程替代后替代前⎧⎪⎪⎨⎪⎪⎩（n-1)个KCL 方程[b-(n-1)]个KVL 方程(b-1)个元件方程第k 条支路方程第k 条支路方程方程不变解不变替换前后方程组解不变；电路响应不变方程不变方程不变或或学MOOC中国大学MOO C 中国大学MO OC学MOOC中国大学MOOC中国大学MO OC学MOOC中国大学MOOC中国大学MO OC学MOOC中国大学MOOC中国大学MO OC学MOOC中国大学MOOC中国大学MO OC学MOO C中国大学MO O C中国大学M O OC1.替代定理既适用于线性电路，也适用于非线性电路。

4.2 替代定理对于一个电路，若某一支路电压为uk 、电流为ik，那么这条支路就可以用一个电压等于uk的独立电压源，或者用一个电流等于ik 的独立电流源，或用大小为R=uk/i k的电阻来替代，替代后电路中所有元件或支路的电压、电流均保持原值(解答唯一)。

1.替代定理第 1 页替代定理支路i k+–u k+–u k i k +–u k u=Rii ki=i k u=Riiuu=u k 工作点等效伏安注意：不是伏安特性等效第 2 页Ai k+–u k支路kA+–u k证毕!2. 定理的证明u k u k＋＋Ai k+–u k支路k+–u ku k u k=0第 3 页＋310＋＋32＋替代前后KCL、KVL关系相同，但“替代” “等效变换”。

替代定理既适用于线性电路，也适用于非线性电路。

注意“替代”仅仅是在工作点等效，不是伏安特性等效。

替代后电路必须有唯一解:替代后不能出现纯电压源回路和纯电流源节点（包括广义节点）替代后其余支路及参数不能有任何改变。

第 5 页有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）1.5A－－－－－1.5A2.5A1.5A 1A－＋－－－？－？第＋U ＋6A=+–+U 0.50.530V1 0.5＋6A–+U'0.50.510.5 30V＋–+0.50.510.56AU''第8 页有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）– ＋+6AU''。

替代定理
替代定理（substitution theorem ）
如果已知电路中第 k 条支路的电压 uk 和电流 ik ，那么无论该条支路是由何种元件构成的，它都可以用电压等于 uk 的理想电压源或电流等于 ik 的理想电流源去替代，替代之后，电路中其他支路的电压和电流均不变。

推论：如果第 k 条支路的电压 uk 等于 0 ，那么该支路可用一条短路线去替代；如果第 k 条支路的电流 ik 等于 0 ，那么该支路可用一对断开的节点去替代。

例 4.2-1 图 4.2-2 （ a ）所示电路为电桥电路，当通过电阻 Rg 的电流 Ig=0 时，电桥达到平衡。

Us=4.5V ， R1=1K Ω， R2=10K Ω， R3 为可变电阻， R4 为被测电阻，现调节电阻 R3 ，当 R3=0.5K Ω时 , 电桥达到平衡。

求被测电阻 R4 及电压源供出的电流 I 。

解：当电桥平衡时，，则 Rg 电阻上的电压。

由于，根据替代定理， ab 支路可用一条短路线替代，如图 4.2-2 （ b ）所示。

显然，
，
即
又由于，根据替代定理， ab 支路可用一对断开的节点替代，如图 4.2-2 （ c ）所示。

则
所以，
上面两式相除，得
因此，被测电阻为
再由图 4.2-2 （ b ），得电桥平衡时， c 、 d 两端的等效电阻为
Rcd= （ R1 ∥ R2 ） + （ R3 ∥ R4 ） = （ 1K ∥ 10K ） + （ 0.5K ∥ 5K ）
=1.364K Ω
所以，平衡时电压源供出的电流
注意：替代定理对于线性电路和非线性电路都是成立的。

一、实验目的1. 理解替代定理的基本概念和适用条件。

2. 验证替代定理在电路分析中的应用，加深对基尔霍夫定律、叠加定理、戴维南定理等电路基本定律的理解。

3. 提高电路分析的实际操作能力，培养严谨的科学实验态度。

二、实验原理替代定理是电路理论中的一个重要定理，它指出：在一个线性电路中，如果一个支路中的电流或电压可以单独由一个电源或一组电源提供，那么这个支路可以用一个等效电源来替代，而不影响电路中其他部分的工作。

具体来说，替代定理可以分为以下两种情况：1. 电流源替代定理：在电路中，一个电流源可以用一个等效电压源来替代，其等效电压等于电流源的内阻乘以电路中电流源两端的开路电压。

2. 电压源替代定理：在电路中，一个电压源可以用一个等效电流源来替代，其等效电流等于电路中电压源两端的短路电流除以电压源的内阻。

三、实验仪器与材料1. 电路实验箱2. 电源（直流稳压电源）3. 电阻器4. 电位器5. 电流表6. 电压表7. 连接线8. 示波器（可选）四、实验步骤1. 搭建实验电路：根据实验要求，搭建一个包含电流源或电压源的电路。

电路中应包含电阻、电位器等元件，以便观察替代定理的应用效果。

2. 测量电路参数：在搭建好的电路中，分别测量电路中各个元件的电压和电流值，记录数据。

3. 应用替代定理：- 对于电流源替代定理，将电流源替换为一个等效电压源，计算等效电压源的值，并将电流源从电路中移除。

- 对于电压源替代定理，将电压源替换为一个等效电流源，计算等效电流源的值，并将电压源从电路中移除。

4. 重新测量电路参数：在替换电流源或电压源后，再次测量电路中各个元件的电压和电流值，记录数据。

5. 对比分析：将替换前后测量得到的数据进行对比分析，验证替代定理的正确性。

五、实验结果与分析1. 电流源替代定理：通过实验，我们发现替换电流源后的等效电压源与原电流源的开路电压相等，电路中其他部分的电压和电流值没有发生变化。

2. 电压源替代定理：同样地，替换电压源后的等效电流源与原电压源的短路电流相等，电路中其他部分的电压和电流值也没有发生变化。

3.2 替代定理1. 替代定理的内容替代定理：对于电路中任意一个端口而言，如果其端口电压为u ，则可以用一个电压为u 的电压源替代，如果其端口电流为i ，则可以用一个电流为i 的电流源替代，被替代端口之外的电路应保持不变。

替代定理听起来好像很有道理，事实也的确如此。

电路教材中有替代定理的证明过程，其实根本不用证明。

稍微一想就知道替代定理是成立的。

因为对于一个电压源来说，其电流完全由外接电路决定。

既然替代后，被替代端口之外的电路保持不变，那么自然端口电流也不变，对于外电路来说，替代前后是等效的。

从这个意义上说，其实替代定理其实就是一种等效变换。

2. 巧用替代定理从替代定理的内容很容易看出来替代定理是局部电路的等效变换，只能起到局部简化的作用。

因此替代定理不是一种直接求解电路的方法，只是一种进行电路局部简化的方法。

即便如此，如果我们善用替代定理，有时也会收到非常好的效果。

下面我举两个例子。

例1：求图1（a ）所示电路的i 。

这个电路看起来很复杂的样子，但仔细观察就会发现右侧三个支路并联，且由于短路线的存在，电压一定为零，根据替代定理，就可以用一个电压为零的电压源替代。

电压为零的电压源其实就是短路线，因此右侧三个支路可以全部去掉，替代成短路线，如图1（b ）所示。

此时，显然可以求出3A i =。

可见巧用替代定理后，电路分析变得很简单。

15V15V （a ）例1电路 （b ）用短路先替代图1 巧用替代定理例1电路例2：求图2（a ）所示电路的i 。

仔细观察会发现100欧姆电阻与电流源串联支路的电流为6A ，既然如此，根据替代定理，100欧姆电阻与6A 电流源串联，可以用6A 的电流源替代，如图2（b ）所示，就好像100欧姆电阻消失了一样。

此时很容易看出4A i =。

可见，通过替代，电路分析变得更简单了。

（a）例2电路（b）用电流源替代图2 巧用替代定理例2的电路3.问与答问：替代定理看起来与等效变换很像，它们之间有何异同？答：替代定理与等效变换的关系很难说得清楚。