3.3 替代定理
- 格式:pdf
- 大小:517.83 KB
- 文档页数:4


3.3 替代定理替代定理是数理逻辑中的重要概念,它在证明某些命题时有着重要的作用。
在数理逻辑中,有时我们需要通过一些等价的命题来证明一个命题是否成立。
这时候替代定理就非常有用了。
替代定理的定义替代定理指的是:设P(x)为一个一元谓词公式,x∈D,D为某个集合,a,b为该集合中的元素,则当a=b时,P(a)与P(b)等价。
这里的“等价”指的是指当a=b时,P(a)为真当且仅当P(b)为真。
换句话说,如果我们要证明一个一元谓词公式在某个集合D中成立,我们只需要证明当a=b时,该一元谓词公式的真值不变,即P(a)与P(b)等价,就可以得出该一元谓词公式在集合D中成立。
举个例子假设我们要证明命题:对于任意正整数x,都存在正整数y,使得x∗y=1。
我们可以使用替代定理进行证明。
我们假设有两个正整数a和b,且a=b。
我们需要证明xa=1当且仅当xb=1。
首先,如果xa=1,则有a除以x的余数为0。
因为x为正整数,所以a≥x,那么a=mx,其中m为正整数,所以xa=(mx)a=ma×x,因为xa=1,所以ma=1,也就是a的倒数是x。
替代定理在证明一些命题时非常有用,尤其是涉及到等价命题的证明。
它可以帮助我们简化证明过程,减少证明步骤,使得证明更加简单、直观。
此外,在离散数学中,替代定理也被广泛地应用于图论、布尔代数、组合数学等领域。
它可以帮助我们推导出一些定理,进而解决一些复杂问题。
总结替代定理是数理逻辑中的一个重要概念,它可以帮助我们证明一些等价命题。
使用替代定理可以大大简化证明过程,减少证明步骤,在离散数学中也有广泛的应用。
因此,学会使用替代定理对于理解数理逻辑、离散数学等领域都是非常重要的。


等效变换和替代定理等效变换是指在不改变电路特性的情况下,通过改变电路中元件的参数或者改变元件的位置,使得电路的形式发生变化,但是电路的特性不变。
等效变换是电路分析中常用的一种方法,可以简化电路分析的过程,提高电路分析的效率。
替代定理是指在电路中,任何两个电阻或电源可以互相替代,只要它们的电压和电流关系相同。
替代定理是电路分析中常用的一种方法,可以简化电路分析的过程,提高电路分析的效率。
下面分别对等效变换和替代定理进行详细介绍:一、等效变换1. 电阻的串并联变换在电路中,若有多个电阻串联或并联,可以通过串并联变换将它们简化为一个等效电阻。
串并联变换的原理是根据欧姆定律和基尔霍夫定律,将多个电阻串联或并联的电路转化为一个等效电阻的电路。
2. 电压源和电流源的等效变换在电路中,若有多个电压源或电流源,可以通过等效变换将它们简化为一个等效电源。
电压源和电流源的等效变换的原理是根据基尔霍夫定律和欧姆定律,将多个电压源或电流源的电路转化为一个等效电源的电路。
3. 电阻的星三角变换在电路中,若有多个电阻星型连接或三角形连接,可以通过星三角变换将它们简化为一个等效电阻。
星三角变换的原理是根据欧姆定律和基尔霍夫定律,将多个电阻星型连接或三角形连接的电路转化为一个等效电阻的电路。
二、替代定理1. 电阻的替代定理在电路中,任何两个电阻可以互相替代,只要它们的电压和电流关系相同。
电阻的替代定理可以简化电路分析的过程,提高电路分析的效率。
2. 电源的替代定理在电路中,任何两个电源可以互相替代,只要它们的电压和电流关系相同。
电源的替代定理可以简化电路分析的过程,提高电路分析的效率。
总之,等效变换和替代定理是电路分析中常用的两种方法,它们可以简化电路分析的过程,提高电路分析的效率。
在实际应用中,需要根据具体情况选择合适的方法进行电路分析。

《大学电路/电路原理/电路分析》06--替代定理的妙用电学中重要的电路定理有叠加定理、齐性定理、替代定理、戴维宁定理、诺顿定理和最大功率传输定理,在不同的场合解决各类电路问题,真的是太精妙了。
叠加定理把多电源电路变为单电源电路,一下子回到高中物理。
齐性定理体现了线性电路的比例性质,其“倒推法”用在单电源多电阻电路就是一个字--“绝”。
戴维宁定理和诺顿定理特别擅长于只求某一支路参数的场合,把待求支路从电路中一取走,变成开口电路,难度一下降低。
最大功率传输定理将复杂的求导变成求戴维宁/诺顿等效电路中的等效电阻了。
但唯独对替代定理的介绍最少,相应的例题应就更少。
其实替代定理是一个非常棒的定理,用得好,考试时大可以提前交卷!接下来介绍替代定理在推导及计算中的妙用。
1.替代定理替代定理是指已知电路中某一支路的参数,如两端的电压,流过支路的电流,那么该支路可等效为一个电压源,或电流源,又或是一个电阻,如下图所示:其证明过程也是相对简单的,等效为电压源时只需在支路上串联2个大小相等,方向相反的电压源,如下图所示:虚线框内支路电压刚好和下面的电压源抵消了,电压为0,可用一条导线替代,这样就只剩下面那个电压源了,得证。
而等效为电流源时,则需在支路两端并联2个大小相等,方向相反的电流源,如下图所示:虚线框内流过支路的电流和右边的电流源也抵消,电流为0,整个框可以去掉,只剩左边那个电流源了。
2. 替代定理在定理推导中的应用戴维宁定理是指,一个含源一端口可以等效为一个实际电压源模型,在证明时该定理就先替代定理,再用叠加定理来操作的,如下图所示:图中N s表示含源一端口,N0表示无源一端口。
有学生问替代时为什么选电流源而不选电压源,主要是由于在接着使用的叠加定理,将电流源置零时可直接将其断开,方便计算,如果选电压源,置零时就要短接,求解麻烦。
将分电路中求出的电压u叠加,得到表达式为:根据式中的电压电流关系,得到等效电路就是实际电压源模型,即戴维宁等效电路,如下图所示:看到这里,只想喊一句:“太妙了!”3.替代定理在解题中的应用替代定理在一些复杂电路中最能显示它的优势,如下图所示:电路要求电流I1,但电路结构很复杂,支路多,电源、电阻也多,看到都头晕。



替代定理和戴维南定理的区别替代定理和戴维南定理是在数学中常见的两种定理。
替代定理是指在某个集合中,如果任意两个元素可以互相替代而不影响该集合的性质,那么这个集合就是一个简单集合,也称为同构集合。
在其他领域中也有类似的概念,比如在代数学中,同构表示两个代数结构之间的相似性,但并不是确切相等。
戴维南定理是一条关于图论中欧拉回路与欧拉路径的定理,它表明一个无向图存在欧拉回路当且仅当该图中所有节点的度数都是偶数,存在欧拉路径当且仅当只有两个节点的度数是奇数。
两个定理之间的主要区别在于所适用的领域和应用范围。
替代定理可以用于任何领域,只要满足互相替代不影响该集合的特性即可。
而戴维南定理只适用于图论中欧拉回路和欧拉路径的解决方案。
此外,两个定理还有其他明显的区别。
替代定理涉及同构,即两个结构可以替代为同一个结构而不影响整个系统的特性。
而戴维南定理基于图中节点的度数,涉及到图的具体性质。
因此,两个定理适用的场景和方法有所不同。
另一个不同点是两个定理适用的范围。
替代定理通常适用于各种数据结构和代数结构等领域,比如在代数学中,同构可以帮助我们判断两个结构之间的相似性,从而推导出它们之间的关系。
而戴维南定理只适用于欧拉回路和欧拉路径的特殊情况中,因此只能用于相关的图论问题中。
最后,两个定理在解决问题时也有所不同。
替代定理的目的是确定不同的结构之间的相似性,以便更好地理解它们之间的关系。
而戴维南定理的目的是找到一条特定的路径或回路,从而解决有关欧拉回路和欧拉路径的问题。
总的来说,两个定理有着明显的区别,包括适用的领域,应用范围,涉及的领域和方法。
理解这些区别可以帮助学者更好地了解它们各自的应用场景和应用方法,以便更好地解决特定的问题。

3.2 替代定理1. 替代定理的内容替代定理:对于电路中任意一个端口而言,如果其端口电压为u ,则可以用一个电压为u 的电压源替代,如果其端口电流为i ,则可以用一个电流为i 的电流源替代,被替代端口之外的电路应保持不变。
替代定理听起来好像很有道理,事实也的确如此。
电路教材中有替代定理的证明过程,其实根本不用证明。
稍微一想就知道替代定理是成立的。
因为对于一个电压源来说,其电流完全由外接电路决定。
既然替代后,被替代端口之外的电路保持不变,那么自然端口电流也不变,对于外电路来说,替代前后是等效的。
从这个意义上说,其实替代定理其实就是一种等效变换。
2. 巧用替代定理从替代定理的内容很容易看出来替代定理是局部电路的等效变换,只能起到局部简化的作用。
因此替代定理不是一种直接求解电路的方法,只是一种进行电路局部简化的方法。
即便如此,如果我们善用替代定理,有时也会收到非常好的效果。
下面我举两个例子。
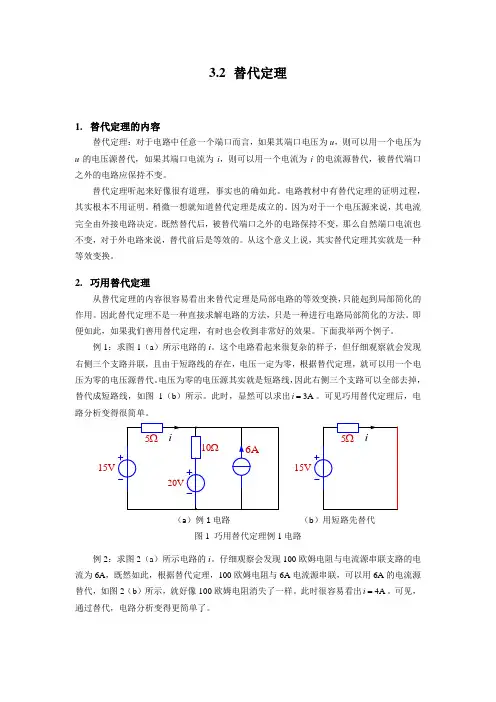
例1:求图1(a )所示电路的i 。
这个电路看起来很复杂的样子,但仔细观察就会发现右侧三个支路并联,且由于短路线的存在,电压一定为零,根据替代定理,就可以用一个电压为零的电压源替代。
电压为零的电压源其实就是短路线,因此右侧三个支路可以全部去掉,替代成短路线,如图1(b )所示。
此时,显然可以求出3A i =。
可见巧用替代定理后,电路分析变得很简单。
15V15V (a )例1电路 (b )用短路先替代图1 巧用替代定理例1电路例2:求图2(a )所示电路的i 。
仔细观察会发现100欧姆电阻与电流源串联支路的电流为6A ,既然如此,根据替代定理,100欧姆电阻与6A 电流源串联,可以用6A 的电流源替代,如图2(b )所示,就好像100欧姆电阻消失了一样。
此时很容易看出4A i =。
可见,通过替代,电路分析变得更简单了。
(a)例2电路(b)用电流源替代图2 巧用替代定理例2的电路3.问与答问:替代定理看起来与等效变换很像,它们之间有何异同?答:替代定理与等效变换的关系很难说得清楚。
替代定理的内容
替代定理是博弈论中的一个著名定理,它指出在特定情况下,博弈的解并非一定是纳什平衡,而是需要通过引入替代方案来解决冲突。
具体来说,如果博弈有两个或多个参与者,并且每个参与者都有两个或多个可选行动,那么替代定理告诉我们,存在一种替代方案,使得所有参与者都更愿意选择这个替代方案,而且它一定是纳什平衡的。
替代定理的应用范围非常广泛,它可以用来解决许多实际问题,例如博弈论、信息经济学、公共政策等。
在博弈论中,替代定理为设计激励机制提供了一种重要思路,即在博弈中引入替代方案,使得参与者更愿意选择合作而不是对抗。
在信息经济学中,替代定理可以用来解释为什么市场失灵的情况经常出现,因为市场参与者往往无法完全了解市场的情况,导致他们无法做出最优决策。
在公共政策中,替代定理可以用来指导政策制定,即通过引入替代方案来缓解政策带来的负面影响。
替代定理是博弈论中一个非常重要的定理,它为我们提供了解决冲突的一种重要思路,可以帮助我们更好地理解博弈论中的各种现象。
替代定理和戴维南定理的区别
替代定理和戴维南定理是数学中常用的两个定理,它们在证明数学问题时起到了重要的作用。
虽然它们都是定理,但是它们的应用场景和证明方法却有所不同。
替代定理是指在证明一个命题时,可以用它的逆否命题来代替原命题。
逆否命题是指将原命题的否定和逆序同时进行的命题。
例如,原命题为“如果A,则B”,则逆否命题为“如果非B,则非A”。
替代定理的应用场景很广泛,可以用于证明各种数学问题,例如证明两个角度相等、两个线段相等等等。
替代定理的证明方法也比较简单,只需要将原命题的逆否命题进行推导即可。
而戴维南定理则是指在证明一个命题时,可以将原命题转化为等价命题来证明。
等价命题是指两个命题具有相同的真值,例如“A或非A”就是一个等价命题。
戴维南定理的应用场景也很广泛,可以用于证明各种数学问题,例如证明两个三角形全等、两个角度相等等等。
戴维南定理的证明方法相对于替代定理来说稍微复杂一些,需要通过一系列的推导和变形来得到等价命题。
总的来说,替代定理和戴维南定理都是数学中常用的定理,它们在证明数学问题时都有着重要的作用。
但是它们的应用场景和证明方法却有所不同,需要根据具体的问题来选择使用哪种定理。
在实际应用中,我们可以根据问题的特点来灵活运用这两种定理,以便更好地解决数学问题。