牛顿第二定律(整体法与隔离法)

牛顿第二定律——连接体问题（整体法与隔离法）一、连接体：当两个或两个以上的物体通过绳、杆、弹簧相连，或多个物体直接叠放在一起的系统二、处理方法——整体法与隔离法系统运动状态相同整体法问题不涉及物体间的内力 使用原则三、连接体题型：1【例1】A、B 平力N F A 6=推A ，用水平力N F B 3=【练1】如图所示，质量为M 的斜面A 在水平向左的推力F 作用下，A 与B 体B 的质量为m ，则它们的加速度a A. ()(,sin μθ++==g m M F g a B. θθcos )(,cos g m M F g a +==C. ()(,tan μθ++==g m M F g a D. gm M F g a )(,cot +==μθ【练2】如图所示，质量为2m 的物体2滑定滑轮连接质量为1m 的物体，与物体A. 车厢的加速度为θsin gB. 绳对物体1的拉力为θcos 1gm C. 底板对物体2的支持力为g m m )(12-D. 物体2所受底板的摩擦力为θtan 2g m m g ，m B =0.4kg ，盘C 的质量O 处的细线瞬间，木F BC 多大？（g 取10m/s 2）连接体作业1、如图所示，小车质量均为M ，光滑小球P 的质量为m ，绳的质量不计，水平地面光滑。

要使小球P 随车一起匀加速运动（相对位置如图所示），则施于小车的水平拉力F 各是多少？（θ已知）球刚好离开斜面 球刚好离开槽底F= F= F= F=2、如图所示，A 、B 质量分别为m1，m2，它们在水平力F 的作用下均一起加速运动，甲、乙中水平面光滑，两物体间动摩擦因数为μ，丙中水平面光滑，丁中两物体与水平面间的动摩擦因数均为μ，求A 、B 间的摩擦力和弹力。

f= f= F AB = F AB = 3、如图所示，在光滑水平桌面上，叠放着三个质量相同的物体，用力推物体a ，使三个物体保持静止，一起作加速运动，则各物体所受的合外力 （ ） A ．a 最大 B ．c 最大 C ．同样大 D ．b 最小4、如图所示,小车的质量为M,的前端相对于车保持静止,A.在竖直方向上,B.在水平方向上,C.若车的加速度变小,D.若车的加速度变大,5、物体A 、B 叠放在斜面体C 上，物体的作用下一起随斜面向左匀加速运动的过程中，物体A 、B摩擦力为2f F ，（02≠f F ），则（A. 01=f F B. 2f F C.1f F 水平向左 D. 2f F 6、如图3所示，质量为M A. 地面对物体M B. 地面对物体M C. 物块m D. 地面对物体M 7、如图所示，质量M ＝8kg 到1.5m/s μ＝0.28、如图6所示，质量为A m 的物体A 沿直角斜面C 9、如图10所示，质量为M 的滑块C B B 、2a F a b c。

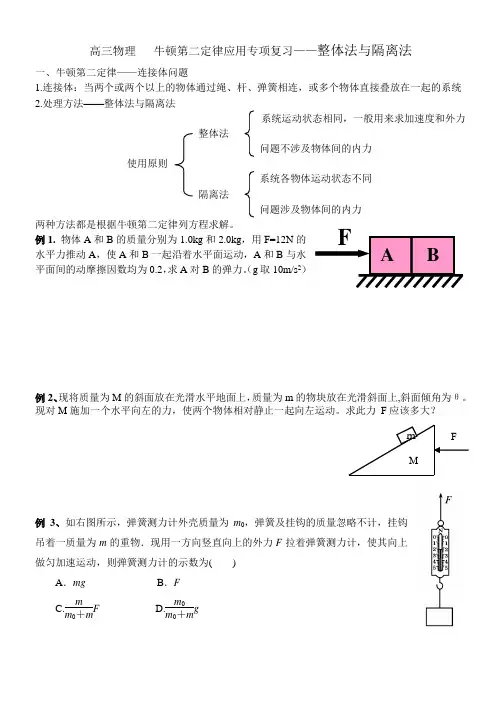
高三物理 牛顿第二定律应用专项复习——整体法与隔离法一、牛顿第二定律——连接体问题1.连接体：当两个或两个以上的物体通过绳、杆、弹簧相连，或多个物体直接叠放在一起的系统2.处理方法——整体法与隔离法系统运动状态相同，一般用来求加速度和外力整体法问题不涉及物体间的内力使用原则系统各物体运动状态不同隔离法问题涉及物体间的内力两种方法都是根据牛顿第二定律列方程求解。

例1. 物体A 和B 的质量分别为1.0kg 和2.0kg ，用F=12N 的水平力推动A ，使A 和B 一起沿着水平面运动，A 和B 与水平面间的动摩擦因数均为0.2，求A 对B 的弹力。

（g 取10m/s 2）例2、现将质量为M 的斜面放在光滑水平地面上，质量为m 的物块放在光滑斜面上,斜面倾角为θ。

现对M 施加一个水平向左的力，使两个物体相对静止一起向左运动。

求此力 F 应该多大？例3、如右图所示，弹簧测力计外壳质量为m 0，弹簧及挂钩的质量忽略不计，挂钩吊着一质量为m 的重物．现用一方向竖直向上的外力F 拉着弹簧测力计，使其向上做匀加速运动，则弹簧测力计的示数为( )A ．mgB ．FC.m m 0＋m FD.m 0m 0＋mg例4、在水平桌面上叠放着A 、B 物体,如图.B 与桌面间的摩擦系数为0.4，两物体的质量分别为m A =2kg ，m B =3kg 用30N 的水平力F 拉B 时，AB 未产生相对滑动,求A 受到的摩擦力.隔离法例5、.如图所示,质量为M 的木箱放在水平面上,木箱中的立杆上套着一个质量为m 的小球,开始时小球在杆的顶端,由静止释放后,小球沿杆下滑的加速度为重力加速度的1/2,即a=g /2,则小球在下滑的过程中,木箱对地面的压力为多少?●针对训练1．如图，质量分别为m 1、m 2的两个物体通过轻弹簧连接，在力F 的作用下一起沿水平方向做匀加速直线运动（m 1在光滑地面上，m 2在空中），力F 与水平方向的夹角为θ，则m 1的加速度大小为（ ）A ．12cos F m m θ+ B ．2sin F m θ C ．12sin F m m θ+ D ．1cos F m θ2、如图所示，五个木块并排放在水平地面上，它们的质量相同，与地面的摩擦不计。

牛顿第二定律类型题——连接体问题连接体问题的分析方法1.整体法：连接体中的各物体如果 ，求加速度时可以把连接体作为一个整体。

运用 列方程求解。

2.隔离法：如果要求连接体间的相互作用力，必须隔离其中一个物体，对该物体应用 求解，此法称为隔离法。

3.整体法与隔离法是相对统一，相辅相成的。

本来单用隔离法就可以解决的连接体问题，但如果这两种方法交叉使用，则处理问题就更加方便。

如当系统中各物体有相同的加速度，求系统中某两物体间的相互作用力时，往往是先用 法求出，再用 法求 。

【当堂清】1. 两物体A 和B ，质量分别为m 1和m 2，互相接触放在光滑水平面上，如图所示，对物体A 施于水平推力F ，则物体A 对物体B 的作用力等于：A. m 1F /(m 1+m 2)B. m 2F /(m 1+m 2)C. FD. m 1F /m 22.两个质量相同的物体1和2紧靠在一起放在粗糙水平桌面上（滑动摩擦因数为μ），如图所示。

如果它们分别受到水平推力F 1和F 2，且F 1>F 2，则1施于2的作用力的大小为：A. F 1B. F 2 -μm 2gC. (F 1+F 2)/2D. (F 1-F 2)/23.如图所示，在光滑的水平面上有等质量的五个物体，每个物体的质量为m 。

若用水平推力F 推1号物体，求2、3号物体间的压力为多大?4.如图所示：把质量为M 的物体放在光滑．．的水平．．高台上，用一条可以忽略质量而且不变形的细绳绕过定滑轮把它与质量为m 的物体连接起来，求：①物体M 和物体m 的运动加速度各是多大？②细绳中的拉力为多大？5.用细绳连接绕过定滑轮的物体M 和m ，已知M>m ，可忽略阻力，求：物体M 和m 的共同加速度a 和细绳中的拉力。

6.一人在井下站在吊台上，用如图所示的定滑轮装置拉绳把吊台和自己提升上来。

图中跨过滑轮的两段绳都是竖直的且不计摩擦。

吊台的质量m=15kg，人的质量为M=55kg起动时吊台向上的加速度是a=0.2m/s2，求这时人对吊台的压力。

牛顿第二定律——连接体问题（整体法与隔离法）例1.两个物体A 和B ，质量分别为m 1和m 2，互相接触放在光滑水平面上，如图所示，对物体A 施以水平的推力F ，则物体A 对物体B 的作用力等于（ ）A.F m m m 211+ B.F m m m 212+ C.FD.F m m21扩展：1.若m 1与m 2于 。

2.如图所示，倾角为α的斜面上放两物体m 1和m 2，使两物加速上滑，不管斜面是否光滑，【例1】A 、B kg m B 6=，今用水平力N F A 6=推A ，用水平力N F B 3=的作用力有多大？8.如图所示，质量分别为m 和2m 的两物体A 、B 最大摩擦力为A 物体重力的μ倍，若用水平力分别作用在A 则作用于A 、B 上的最大拉力F A 与F B 之比为多少？10．如图所示，质量为m 的物体A 放置在质量为M 的物体B 上，B 与弹簧相连，它们一起在光滑水平面上做简谐运动，振动过程中A 、B 之间无相对运动.设弹簧的劲度系数为k .当物体离开平衡位置的位移为x 时，A 、B 间摩擦力的大小等于（ ）A ．0B ．kxC ．kx M mD ．kx m M m )(+【练1】如图所示，质量为M 的斜面A 在水平向左的推力F 作用下，A 与B 物体B 的质量为m ，则它们的加速度a A. ()(,sin μθ++==g m M F g a B. θθcos )(,cos g m M F g a +==C. ()(,tan μθ++==g m M F g a D. g m M F g a )(,cot +==μθ【练2】如图所示，质量为2m 的物体2放在正沿平直轨道向右行驶的车厢底板上，并用竖直细绳通过光滑定滑轮连接质量为1m 的物体，与物体1相连接的绳与竖直方向成θ角，则（ ）A. 车厢的加速度为θsin gB. 绳对物体1的拉力为θcos 1gmC. 底板对物体2的支持力为g m m )(12-D. 物体2所受底板的摩擦力为θtan 2g m2、连接体整体内部各部分有不同的加速度：【例2有一个环，箱和杆的总质量为M ，环的质量为m 加速度大小为a 时（a ＜g A. Mg + mg B. Mg —1.（★★★）如图2-8所示，质量为M 端固定一个质量为m 的小球，小球上下振动时，压力为零瞬间，小球的加速度大小为A.gB.m mM - g C.0D. mm M +g【例12】如图，底座A 上装有一根直立竖杆，其总质量为M 量为m 的环B ，它与杆有摩擦。

动力学中的整体法与隔离法1．整体法的选取原则：若连接体内各物体具有相同的加速度，且不需要求物体之间的作用力，可以把它们看成一个整体来分析整体受到的外力，应用牛顿第二定律求出加速度(或其他未知量)．2．隔离法的选取原则：若连接体或关联体内各物体的加速度不相同，或者要求出系统内两物体之间的作用力时，就需要把物体从系统中隔离出来，应用牛顿第二定律列方程求解．3．整体法、隔离法交替运用原则：若连接体内各物体具有相同的加速度，且要求物体之间的作用力时，可以先用整体法求出加速度，然后再用隔离法选取合适的研究对象，应用牛顿第二定律求作用力．即“先整体求加速度，后隔离求内力”．当系统内各物体具有相同的加速度时，应先把这个系统当作一个整体（即看成一个质点），分析受到的外力及运动情况，利用牛顿第二定律求出加速度．如若要求系统内各物体相互作用的内力，则把物体隔离，对某个物体单独进行受力分析，再利用牛顿第二定律对该物体列式求解．隔离物体时应对受力少的物体进行隔离比较方便。

【例1】如图所示的三个物体A 、B 、C ，其质量分别为m 1、m 2、m 3，带有滑轮的物体B 放在光滑平面上，滑轮和所有接触面间的摩擦及绳子的质量均不计．为使三物体间无相对运动，则水平推力的大小应为F ＝__________。

【解析】【例2】如图所示，n 个质量都是m 的立方体放在光滑的水平桌面上，若以大小为F 的恒力推第一块立方体，试求：第2个立方体作用于第3个立方体的力为__________。

【解析】【例3】如图所示，物体M 、m 紧靠着置于摩擦系数为μ的斜面上，斜面的倾角为θ，现施加一水平力F 作用于M ，M 、m 共同向上作加速运动，求它们之间相互作用力的大小。

【解析】两个物体具有相同的沿斜面向上的加速度，可以把它们当成一个整体（看作一个质点），其受力如图所示，建立坐标系，则：θθsin cos )(1F g m M F ++= (1) a m M g m M f F )(sin )(cos 1+=+--θθ （2）且：11F f μ= （3） 要求两物体间的相互作用力，应把两物体隔离开．对m 受力如图所示，则0cos 2=-θmg F (4) ma mg f F =--θsin '2 （5）且：22F f μ= （6）联立以上方程组，解之：)()sin (cos 'm M mFF +-=θμθ。

整体法与隔离法使一个物体从周围环境中独立出来单独进行分析的方法称为隔离法。

它的特点是将注意力集中到了一个质点上。

整体法是将一个质点组作为研究对象进行分析的方法。

它的特点是将注意力同时集中到了多个质点组成的系统上。

一般地，隔离法是研究问题的基本方法。

整体法往往是通过隔离法和相关物理规律推导而得出的规律。

第一部分 整体的牛顿第二定律下面我们以两个质点A 、B 构成的系统为例，根据一个质点的牛顿第二定律和第三定律得出系统的牛顿第二定律。

我们将A 所受的外力之和（不包括B 对A 的作用力）设为外A F ，B 所受的外力之和（不包括A 对B 的作用力）设为外B F 。

分别对A 和B 应用一个质点的牛顿第二定律，有：A A BA A a m F F =+外B B AB B a m F F =+外由牛顿第三定律有：BA AB F F -=（其中负号表示方向相反）由上面三式可得：B B A A B A a m a m F F +=+外外其中外外B A F F +为A 、B 构成的系统所受的外力之和，我们用一个符号合外F 来表示，有：B B A A a m a m F +=合外这说明，一个系统所受的外力之和等于系统内各物体质量与之加速度乘积的矢量和。

这就是整体的牛顿第二定律。

在不同的环境中，整体的牛顿第二定律有它不同的表达形式，下面我们分情况进行说明：1．系统内各物体都处于平衡状态时，0=合外F 。

这里的系统内各物体都处于平衡状态，指的是系统内物体的加速度都为零。

即0==B A a a ，很显然，有0=合外F 。

系统内各物体都处于平衡状态，具体来说又分为下面几种情况：（1）系统内各物体均处于静止状态；（2）系统内各物体以相同的速度做匀速直线运动；（3）系统内各物体以不同的速度做匀速直线运动；（4）系统内有些物体做匀速直线运动，而另一些物体保持静止状态。

例1：（第1页第1题）m 做匀速直线运动而M 保持静止，由整体的牛顿第二定律，有：0=合外F 。

牛顿运动定律的应用之用整体法、隔离法巧解连接体问题1.连接体的分类根据两物体之间相互连接的媒介不同，常见的连接体可以分为三大类。

(1)绳(杆)连接：两个物体通过轻绳或轻杆的作用连接在一起；(2)弹簧连接：两个物体通过弹簧的作用连接在一起；(3)接触连接：两个物体通过接触面的弹力或摩擦力的作用连接在一起。

2.连接体的运动特点轻绳——轻绳在伸直状态下，两端的连接体沿绳方向的速度总是相等。

轻杆——轻杆平动时，连接体具有相同的平动速度；轻杆转动时，连接体具有相同的角速度，而线速度与转动半径成正比。

轻弹簧——在弹簧发生形变的过程中，两端连接体的速率不一定相等；在弹簧形变最大时，两端连接体的速率相等。

学科，网特别提醒(1)“轻”——质量和重力均不计。

(2)在任何情况下，绳中张力的大小相等，绳、杆和弹簧两端受到的弹力大小也相等。

3.连接体问题的分析方法(1)分析方法：整体法和隔离法。

(2)选用整体法和隔离法的策略：①当各物体的运动状态相同时，宜选用整体法；当各物体的运动状态不同时，宜选用隔离法；②对较复杂的问题，通常需要多次选取研究对象，交替应用整体法与隔离法才能求解。

4. 整体法与隔离法的选用方法（1）整体法的选取原则若在已知与待求量中一涉及系统内部的相互作用时，可取整体为研究对象，分析整体受到的外力，应用牛顿第二定律列方程。

当系统内物体的加速度相同时：a m m m F n )...(21+++=；否则n n a m a m a m F +++=...2211。

（2）隔离法的选取原则若在已知量或待求量中涉及到系统内物体之间的作用时，就需要把物体从系统中隔离出来，应用牛顿第二定律列方程求解．（3）整体法、隔离法的交替运用若连接体内各物体具有相同的加速度，且要求物体之间的作用力时，可以先用整体法求出加速度，然后再用隔离法选取合适的研究对象，应用牛顿第二定律求作用力．即“先整体求加速度，后隔离求内力”．【典例1】如图所示，两个质量分别为m 1＝3 kg 、m 2＝2 kg 的物体置于光滑的水平面上，中间用轻质弹簧测力计连接。