2015年4月2015届高三第三次全国大联考(江苏版)数学卷-掌门1对1

2015年第三次全国大联考【四川卷】-掌门1对1 理科综合能力测试 答题卡
姓名：______________班级：______________
准考证号
[来源:学科网ZXXK]
物理部分
1、[ A ] [ B ] [ C ] [ D ]
2、[ A ] [ B ] [ C ] [ D ]
3、[ A ] [ B ] [ C ] [ D ]
4、[ A ] [ B ] [ C ] [ D ]
5、[ A ] [ B ] [ C ] [ D ]
6、[ A ] [ B ] [ C ] [ D ]
7、[ A ] [ B ] [ C ] [ D ]
【8题】
【9题】 缺考标记
考生禁止填涂缺考标记！只能
由监考老师负
责用黑色字迹的签字笔填涂。

注意事项 1、答题前，考生先将自己的姓名、准考证号码填写清楚。

2、请将准考证条码粘贴在右侧的[条码粘贴处]的方框内 3、选择题必须使用2B 铅笔填涂；非选择题必须用0.5毫米黑色字迹的签字笔填写，字体工整 4、请按题号顺序在各题的答题区内作答，超出范围的答案无效，在草纸、试卷上作答无效。

5、保持卡面清洁，不要折叠、不要弄破、弄皱，不准使用涂改液、刮纸刀。

6、填涂样例 正确 [■] 错误 [--][√] [×]
条 码 粘 贴 处 （正面朝上贴在此虚线框内）
化学部分
2
【9题】
[来源:学§科§网Z§X§X§K]
【10题】
【11题】
[来源:学+科+网Z+X+X+K]
生物部分
] [ C ] [ D ]
4
【11题】。

第1页 共16页 ◎ 第2页 共16页2015年第三次全国大联考试题【新课标Ⅰ卷】-掌门1对1英 语 试 卷本试卷分第I 卷（选择题）和第II 卷（非选择题）。

考试结束，将本试卷和答题卡一并交回。

第I 卷注意事项：1．答第I 卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

不能答在本试卷上，否则无效。

第一部分听力（共两节，满分30分）做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节（共5小题；每小题1．5分，满分7．5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A 、B 、C 三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. What is Mr. Linton? A. A teacher.B. A doctor.C. A policeman.2. What will the man do?A. Change the plan.B. Wait for a phone callC. Sort things out. 3. What does the woman mean?A. She will not take any medicine.B. She hasn’t got a bad cold.C. She will take some medicine in a week. 4. What do we learn about the woman?A. The woman is planning a trip to Austin.B. The woman hasn’t been to Austin before.C. The woman doesn’t like Austin.5.What can we learn from the conversation? A. The sign is not clear enough. B. The man wants to see the staff. C. The man is in the wrong place.第二节（共15小题；每小题1.5分，满分22.5分)听下面5段对话或独白。

江苏大联考2015届高三第三次联考·数学试卷考生注意:1。

本试卷共160分.考试时间120分钟。

2。

答题前,考生务必将密封线内的项目填写清楚。

3。

请将各题答案填在试卷后面的答题卷上.4.交卷时,可根据需要在加注“”标志的夹缝处进行裁剪。

5.本试卷主要考试内容:前2次联考内容+数列+不等式。

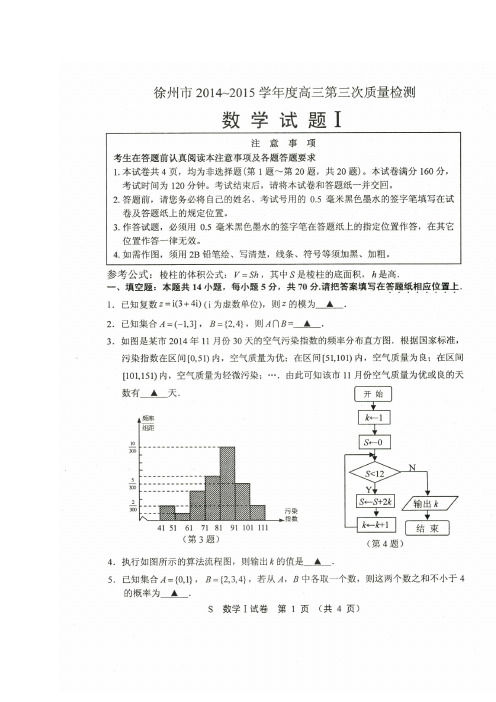
一、填空题:本大题共14小题，每小题5分,共70分。

把答案填在答题卷中的横线上。

1.设集合M={x｜x2+x-6〈0},N={x|1≤x≤3｝,则M∩N=▲.2。

已知数列｛a n}为等差数列，其前9项和为S9=54,则a5=▲.3。

用12米的绳子围成一个矩形,则这个矩形的面积最大值为▲.4.在等比数列{a n}中,a1=2,若a1,2a2，a3+6成等差数列，则a n=▲ .5。

若tan θ=1，则cos 2θ=▲。

,则a10+a13=6。

已知在等比数列｛a n}中，a3+a6=4,a6+a9=12▲。

=7。

已知a>0，b〉0，ab=4，当a+4b取得最小值时，ab▲。

8.已知平面向量a、b,|a|=3,｜b｜=2√3且a—b与a垂直,则a与b的夹角为▲。

9。

设变量x,y满足约束条件{x+y≥3,则目标函数z=2x+3y的最小值与x-y≥-12x-y≤3最大值的和为▲。

10.若对于任意的x〉0,不等式x≤a恒成立,则实数a的取值范围x2+2x+4为▲.11.已知在各项为正的等比数列｛a n}中,a2与a8的等比中项为8，则4a3+a7取最小值时首项a1= ▲.12。

下面图形由小正方形组成，请观察图1至图4的规律,并依此规律,写出第16个图形中小正方形的个数是▲.13.在数列｛a n}中,若存在一个确定的正整数T，对任意n∈N＊满足a n+T=a n，则称{a n｝是周期数列,T叫做它的周期。

已知数列｛x n}满足x1=1,x2=a(a≤1）,x n+2=｜x n+1—x n|，若数列{x n}的周期为3，则{x n｝的前100项的和为▲.的取值范围是14。

（第10题）A B C D E F （第11题）题）P （第5题）开始开始 输入x y ←5 x <4 y ←x 2-2x +2 输出y 结束结束 Y N （第4题）题）时间（小时） 频率频率组距组距0.004 0.008 0.012 0.016 0 50 75 100 125 150 江苏省南通、泰州、扬州、淮安四市2015届高三第三次调研测试数 学 试 题一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．．．．．．．．． 1． 设集合A ={3，m }，B ={3m ，3}，且A =B ，则实数m 的值是的值是 ▲ ． 2． 已知复数z =(1i)(12i)+-(i 为虚数单位)，则z 的实部为的实部为 ▲ ． 3． 已知实数x ，y 满足条件||1||1x y ìíî≤≤,,则z =2x +y 的最小值是的最小值是 ▲ ．4． 为了解学生课外阅读的情况，随机统计了n 名学生的课外阅读时间，所得数据都在[50，150]中，其频率分布直方图如图所示．已知在[50 75)，中的频数为100，则n 的值为的值为 ▲ ．5． 在如图所示的算法流程图中，若输出的y 的值为26，则输入的x 的值为的值为 ▲ ．6． 从集合{1，2，3，4，5，6，7，8，9}中任取一个数记为x ，则log 2x 为整数的概率为为整数的概率为 ▲ ．7． 在平面直角坐标系xOy 中，点F 为抛物线x 2=8y 的焦点，则F 到双曲线2219y x -=的渐近线的距离为的渐近线的距离为▲ ．8． 在等差数列{a n }中，若a n +a n +2=4n +6（n ∈N *），则该数列的通项公式a n = ▲ ． 9． 给出下列三个命题：给出下列三个命题： ①“a ＞b ”是“3a a＞3b b”的充分不必要条件；”的充分不必要条件； ②“α＞β”是“cos α＜cos β”的必要不充分条件；”的必要不充分条件；③“a =0”是“函数f (x ) = x 33+ax 22（x ∈R ）为奇函数”的充要条件．）为奇函数”的充要条件．其中正确命题的序号为其中正确命题的序号为 ▲ ．10．已知一个空间几何体的所有棱长均为1 cm ，其表面展开图如图所示，则该空间几何体的体积，其表面展开图如图所示，则该空间几何体的体积V = ▲ cm 3．PC PD 的最小值为的最小值为 ▲ ．1 1≤，＞.若函数的取值范围为的取值范围为 ▲ ．2112的值为的值为 ▲ ．的取值范围为 ▲ ．＜＜) ABCDA 1 B 1 C E xyO 2 -2 （第16题）题）3p - 32p如图，在平面直角坐标系xOy 中，椭圆221a b +=(a ＞b ＞0)的两焦点分别为F 1(3-，0)，F 2(3，0)，且经过点(3，12)．（1）求椭圆的方程及离心率；）求椭圆的方程及离心率；（2）设点B ，C ，D 是椭圆上不同于椭圆顶点的三点，点B 与点D 关于原点O 对称．设直线CD ，CB ，OB ，OC 的斜率分别为k 1，k 2，k 3，k 4，且k 1k 2=k 3k 4． ①求k1k 2的值；的值；②求OB 2+OC 2的值．的值．18．（本小题满分16分）为丰富市民的文化生活，市政府计划在一块半径为200 m ，圆心角为120°的扇形地上建造市民广场．规划设计如图：内接梯形ABCD 区域为运动休闲区，其中A ，B 分别在半径OP ，OQ 上，C ，D 在圆弧PQ 上，CD ∥AB ；△OAB 区域为文化展示区，AB 长为503m ；其余空地为绿化区域，且CD 长不得超．．．过．200 m． （1）试确定A ，B 的位置，使△OAB 的周长最大？的周长最大？（2）当△OAB 的周长最大时，设∠DOC =2q ，试将运动休闲，试将运动休闲区ABCD 的面积S 表示为q 的函数，并求出S 的最大值．的最大值．ABCDPQ（第18题）题）OyxOF 1F 2 BC （第17题）题）D2)a a2)r 22 CABOPH3的值．的值． D1 B 1 D 1 开始开始 输入x y ←5 x <4 y ←x 2-2x +2 输出y结束结束 Y N 时间（小时）频率频率 组距组距0.004 0.008 0.012 0.016 0 50 75 75 100 125 150 100 125 150 的值是的值是 ▲ ．的实部为的实部为▲ ．的最小值是 ▲ ．100，则n 的值为的值为 ▲ ．的值为的值为 ▲ ．为整数的概率为为整数的概率为 ▲ ．4▲ ．10= ▲ ．DFP其中正确命题的序号为其中正确命题的序号为 ▲ ．= ▲ cm 2PC PD 的最小值为的最小值为 ▲ ．5的取值范围为的取值范围为 ▲ ．的值为的值为▲ ．的取值范围为 ▲ ．＜＜) )ABCDA1 B1 CEFABCDA1 B1 ExyO2 -2 （第16题）题）3p-32p))))22333343222211(33)(0)(33)(0)22--+--+-3yxOF 1F 2BC D2121121) 44)(1)21)33)()33)m n +为等腰梯形．为等腰梯形． ] ，(503625(33cos 3)] ，83cos 3] ，83sin ，) ， ABCDPOABCDP O E F] ，3] ，153)153))a a )1231133)2n -+)232))22)a a)a a)(1)a a aa a a a)()2())2()+-a))-a212记21x x =t ，t ＞1，则11ln t t tx -=，故11ln t x t t-=． 于是，x 1+x 2=x 1(t +1)=21ln t t t -，x 1+x 2-2=212(ln )2ln t t tt--．记函数g (x )=21ln 2x x x--，x ＞1．因22(1)()2x g x x -¢=＞0，故g (x )在(1 )+¥，上单调递增．上单调递增．于是，t ＞1时，g (t )＞g (1)=0．又ln t ＞0，所以，x 1+x 2＞2．……………………………………………………………13分 再证x 1+x 2＜13e a--1．因f (x )=0Ûh (x )=ax -1-x ln x =0，故x 1，x 2也是h (x )的两零点．的两零点． 由()h x ¢=a -1-ln x =0，得x =1ea -(记p =1ea -)．仿（1）知，p 是h (x )的唯一最大值点，故有12()0.h p x p x ìíî＜＞，＜ 作函数h (x )=2()ln ln x p xp x p ---+，则22()()()x p h x x x p -¢=+≥0，故h (x )单调递增．单调递增． 故，当x ＞p 时，h (x )＞h (p )=0；当0＜x ＜p 时，h (x )＜0． 于是，ax 1-1=x 1ln x 1＜11112()ln x x p x p x p-++．整理，得211(2ln )(2ln 1)p a x p ap p p x p +--+--+＞0，即，21111(3e1)eaax x ----+＞0．同理，21122(3e 1)ea a x x ----+＜0．故，21122(3e1)ea a x x ----+＜21111(3e1)ea a x x ----+，1212121()()(3e 1)()a x x x x x x -+---＜，于是，1123e 1ax x -+-＜．综上，2＜x 1+x 2＜13e a--1．………………………………………………………16分) CABOHCABOH2)r 222r 2222r d -3的值．的值． (1AD =-，，1(1,1,1,1,0),0)DB =，(0,0,2)DD =0,0DB DD ×=×=n ，即110,|||10||||AD AD AD ×<>==n n n ，所成角的正弦值为1010．…………………………(110)(10DB DE ==，，，，，00DB DE ×=×=，n ，得，(0,1,2)DC =00DB DC ×=×=，n ，得214||||321ll >==+n n n n ，A B D1 B 1 D 1 ABCDA 1 B 1 C 1 D 1 （第22题答图）xyz所以2314||3321ll -=+，得1l =．所以112AE AA =．……………………………10分23．（本小题满分10分）袋中共有8个球，其中有3个白球，5个黑球，这些球除颜色外完全相同．从袋中随机取出一球，如果取出白球，则把它放回袋中；如果取出黑球，则该黑球不再放回，并且另补一个白球放入袋中．重复上述过程n 次后，袋中白球的个数记为X n ． （1）求随机变量X 2的概率分布及数学期望E (X 2)；（2）求随机变量X n 的数学期望E (X n )关于n 的表达式．的表达式．解：（1）由题意可知X 2=3，4，5． 当X 2=3时，即二次摸球均摸到白球，其概率是P (X 2=3)=11331188C C C C ´=964； 当X 2=4时，即二次摸球恰好摸到一白，一黑球，其概率是P (X 2=4)=1111355411118888C C C C C C C C +=3564； 当X 2=5时，即二次摸球均摸到黑球，其概率是P (X 2=5)=11541188C C C C =516．…… 3分所以随机变量X 2的概率分布如下表：的概率分布如下表：X 2 3 4 5 P964 3564516（一个概率得一分 不列表不扣分）数学期望E (X 2)=935526734564641664´+´+´=．……………………………… 5分 （2）设P (X n =3+k )=p k ，k =0，1，2，3，4，5．则p 0+p 1+p 2+p 3+p 4+p 5=1，E (X n )=3p 0+4p 1+5p 2+6p 3+7p 4+8p 5．P (X n +1=3)=038p ，P (X n +1=4)=58p 0+48p 1，P (X n +1=5)=48p 1+58p 2，P (X n +1=6)=38p 2+68p 3，P (X n +1=7)=28p 3+78p 4，P (X n +1=8)=18p 4+88p 5，………………………7分所以，E (X n +1) =3×38p 0+4×+4×((58p 0+48p 1)+5×)+5×((48p 1+58p 2)+6×)+6×((38p 2+68p 3)+7×)+7×((28p 3+78p 4)+8×)+8×((18p 4+88p 5) =298p 0+368p 1+438p 2+508p 3+578p 4+648p 5 =78(3p 0+4p 1+5p 2+6p 3+7p 4+8p 5)+ p 0+p 1+p 2+p 3+p 4+p 5 =78E (X n )+1． …………………9分 由此可知，E (X n +1)-8=78(E (X n )-8)．又E (X 1)-8=358-，所以E (X n )=13578()88n --．……………………………10分。

2015年第三次全国大联考【浙江卷】-掌门1对1 理科综合能力测试 答题卡姓名：______________班级：______________准考证号1、[ A ] [ B ] [ C ] [ D ]2、[ A ] [ B ] [ C ] [ D ]3、[ A ] [ B ] [ C ] [ D ]4、[ A ] [ B ] [ C ] [ D ]5、[ A ] [ B ] [ C ] [ D ]6、[ A ] [ B ] [ C ] [ D ]7、[ A ] [ B ] [ C ] [ D ]8、[ A ] [ B ] [ C ] [ D ]9、[ A ] [ B ] [ C ] [ D ] 10、[ A ] [ B ] [ C ] [ D ] 11、[ A ] [ B ] [ C ] [ D ] 12、[ A ] [ B ] [ C ] [ D ] 13、[ A ] [ B ] [ C ] [ D ] 14、[ A ] [ B ] [ C ] [ D ] 15、[ A ] [ B ] [ C ] [ D ] 16、[ A ] [ B ] [ C ] [ D ]17、[ A ] [ B ] [ C ] [ D ]18、[ A ] [ B ] [ C ] [ D ]19、[ A ] [ B ] [ C ] [ D ]20、[ A ] [ B ] [ C ] [ D ]【21题】【22题】缺考标记考生禁止填涂缺考标记！只能由监考老师负责用黑色字迹的签字笔填涂。

注意事项 1、答题前，考生先将自己的姓名、准考证号码填写清楚。

2、请将准考证条码粘贴在右侧的[条码粘贴处]的方框内 3、选择题必须使用2B 铅笔填涂；非选择题必须用0.5毫米黑色字迹的签字笔填写，字体工整 4、请按题号顺序在各题的答题区内作答，超出范围的答案无效，在草纸、试卷上作答无效。

5、保持卡面清洁，不要折叠、不要弄破、弄皱，不准使用涂改液、刮纸刀。

高三第三次调研考试数学一卷参考答案一、填空题1.5;2.{2};3.28;4.4;5.12;6.37;7.2-;8.2213x y -=; 9.4π; 10.2; 11.35[.]22; 12.[0,3]; 13.2513; 14. 2e (1,e ). 二、解答题15.解：（1）1cos 3C =，()0,C π∈，22sin 3C ∴=· ……………………………………………………2分 πA B C ++=，()sin sin A B C ∴=+……………………………………………………………………………………3分122sin cos cos sin sin cos 33B C B C B B =+=+，……………………………………………5分 由题意122sin cos 2cos 33B B B +=， 12sin cos 33B B ∴=， tan 2B ∴=·……………………………………………………………7分 （2）由（1）知tan 2B =,6sin 3B ∴=,3cos 3B =·……………………………………………………9分 由正弦定理得sin sin b c B C =，651532223b ∴=⨯=· ………………………………………………11分又6sin 2cos 3A B ==， ………………………………………………………………………………12分1115652sin 522234S bc A ∴==⨯⨯⨯=·………………………………………………………………14分16．（1）∵AE ⊥平面ECD ，CD ⊂平面ECD ，∴AE CD ⊥． 又∵AB //CD ,AB AE ∴⊥．……………………………………………………………2分在矩形ABCD 中，AB AD ⊥，…………………………………………………………………………4分∵AD AE A =，,AD AE ⊂平面ADEAB ∴⊥平面A ． …………………………………………………………………………………6分（2）连AN 交BD 于F 点，连接FM ………………………………………………………………………8分∵AB //CD 且2AB DN =2AF FN ∴= ………………………………………………………………………………………10分又AM =2ME EN ∴//FM ……………………………………………………………………………12分又EN ⊄平面BDM ,FM ⊂平面BDMEN ∴//平面BDM . ………………………………………………………………………………14分17.（1）在Rt △P AE 中，由题意可知APE α∠=，AP =8，则8tan AE α=．所以1322PAE S PA AE α=⨯=.………………………………………………………………………2分同理在Rt △PBF 中，PFB α∠=，PB ＝1,则1tan BF α=, 所以1122tan PBF S PB BF α=⨯=. ……………………………………………………………………4分 故△P AE 与△PFB 的面积之和为132tan 2tan αα+…………………………………………………5分1232tan 2tan αα⨯≥=8, 当且仅当132tan 2tan αα=,即1tan 8α=时取等号, 故当AE =1km,BF =8km 时，△P AE 与△PFB 的面积之和最小. ……………………………………………6分(2)在Rt △P AE 中，由题意可知APE α∠=，则8cos PE α=． 同理在Rt △PBF 中，PEB α∠=，则1sin PF α=． 令81()cos sin f PE PF ααα=+=+，02πα<<， …………………………………………………………8分 则3322228sin cos 8sin cos ()cos sin sin cos f ααααααααα-'=-=， ……………………………………………………………10分令()0f α'=，得1tan 2α=，记01tan 2α=，002πα<<， 当0(0,)αα∈时，()0f α'<，()f α单调递减； 当0(,)2παα∈时，()0f α'>，()f α单调递增． 所以1tan 2α=时，()f α取得最小值， ……………………………………………………………………12分 此时1tan 842AE AP α=⋅=⨯=，2tan BP BF α==． 所以当AE 为4km ，且BF 为2km 时，PE +PF 的值最小．…………………………………………………14分18.（1）由题意23283,23c a a c ==，解得2,3a c ==， 1b ∴=，椭圆方程为2214x y +=· ………………………………………………………………………4分 （2）解法一:12TBC S BC t t ∆=⋅= …………………………………………………………………………6分 直线TB 方程为：11y x t =+，联立221411x y y x t ⎧+=⎪⎪⎨⎪=+⎪⎩，得284E t x t -=+ 所以22284,44t t E t t ⎛⎫-- ⎪++⎝⎭到:TC 30x ty t --=的距离()()()222222242444212994t t t t t t t t d t t t ----+++==+++ ………………………………………………………………8分直线TC 方程为：31y x t =-，联立221431x y y x t ⎧+=⎪⎪⎨⎪=-⎪⎩，得22436F t x t =+ ,2222436,3636t t F t t ⎛⎫- ⎪++⎝⎭，∴TF 22222243623636t t t t t ⎛⎫-⎛⎫=-+- ⎪ ⎪++⎝⎭⎝⎭ ()()()()()()()22222222222222212336129129363636t t t t t t t t tt+++++++===+++ …………………………………10分∴()()()()()()22222222221292121211223636494TEFt t t t t t S TF d t t t t t ∆++++=⋅=⋅⋅=+++++ ∴()()()222236412TBC TEFt t S k S t ∆∆++==+ ……………………………………………………………………………12分令21212t m +=>,则22(8)(24)1619241,3m m k m m m -+==+-≤ ……………………………………………………………………14分当且仅当24m =,即23t =±等号成立, 所以k的最大值为43. ……………………………………………………………………………………16分 解法二:直线TB 方程为：11y x t=+，联立221411x y y x t ⎧+=⎪⎪⎨⎪=+⎪⎩，得284E t x t -=+ (6)分直线TC 方程为：31y x t =-，联立221431x y y x t ⎧+=⎪⎪⎨⎪=-⎪⎩，得22436F t x t =+ ………………………………………8分1sin 21sin 2TBCTEFTB TC BTCS TB TC k S TE TF TE TF ETF ∆∆⋅⋅∠⋅===⋅⋅⋅∠T C T B T E T F x x x x TB TC TE TF x x x x --=⋅=⋅--………………………………10分()()()()2222224368241212436t t ttt t t t t t t t +⋅+=⋅=+⋅++-++…………………………………………………………………12分令21212t m +=>,则22(8)(24)1619241,3m m k m m m -+==+-≤ ……………………………………………………………………14分当且仅当24m =,即23t =±等号成立 所以k 的最大值为43. ………………………………………………………………………………………16分 19.(1)因为n a >,当1n =时,21111122a a a =+,解得11a =.………………………………………………1分由21122n n n S a a =+,当2,n ≥ 21111122n n n S a a ---=+,两式相减，得221111)(+)022n n n n a a a a ----=（．……………………………………………………………2分又因为0n a >,所以1+0n n a a -≠， 所以1=1n n a a --,1(1)1n a a n n =+-⨯=．…………………………………………………………………4分由2246,.b a b a ==得264223a b q b a ===，所以2222(3)n n n b b q --=⋅=⋅． ……………………………………………………………………6分(2)由题意得12,21()23,2()nn n n k k N c n k k N *-*⎧=-∈⎪=⎨⎪⋅=∈⎩， 所以21321242()()m m m T a a a b b b -=+++++++2(121)2(13)31213m mm m m +--=+=+-- ………………………………………………………8分21122122312331m m m m m m T T b m m ---=-=+--⨯=+-所以222121221312(1)333131m m m m m T m m T m m ---+--==-≤+-+- ……………………………………………………10分 故若221mm T T -为{}n c 中的项只能为123,,c c c ．………………………………………………………………11分(Ⅰ)若2122(1)3=131m m m ---+-,则130m -=,所以m 无解． ……………………………………………12分（Ⅱ）若212122(1)3=231031m m m m m ----⇒+-=+- 显然1m =不符合题意，2m =符合题意． 当3m ≥时，即12()31,m f m m -=+-则1()3ln32,m f m m -'=-设1()3ln32,m g m m -=-则12()3(ln3)20m g m -'=->，即1()3ln32m f m m -'=-为增函数，故()(3)0f m f ''≥>，即()f m 为增函数 故()(3)10.f m f >=>故当3m ≥时方程1231=0m m -+-无解，即2m =是方程唯一解。

2015年第三次全国大联考【新课标Ⅰ卷】-掌门1对1理科综合能力测试考试范围：高考全部内容；考试时间：150分钟；有关元素的相对原子质量是：H l C 12 N 14 O 16 S 32 Na 23 Mg 24 Al 27Cl 35．5 Fe 56 Cu 64 Ba 137第I卷一、选择题（本题包括13小题，每小题6分。

在每小题给出的四个选项中，只有一项符合题目要求。

）1．下列有关细胞的结构和功能的叙述中，正确的是（）A．内质网膜成为高尔基体膜的一部分，离不开生物膜的选择透过性B．同一动物个体的神经细胞和肌肉细胞中，不可能存在相同的蛋白质C．吞噬细胞吞噬清除病原体的过程中，细胞膜成为溶酶体膜的一部分D．同一叶肉细胞内的线粒体和叶绿体之间，时刻进行着物质交换2．下列关于细胞的生命历程的叙述正确的是（）A．细胞的全能性是指细胞既能分化,也能恢复到分化前的状态B．正常的人体细胞会随着分裂次数的增多而衰老C．衰老过程中细胞的形态､结构发生变化而功能不变D．环境中的致癌因子会损伤细胞中的DNA,使其产生原癌基因3．肠道病毒EV71为单股正链RNA（+RNA）病毒，是引起手足口病的主要病原体之一，下图为该病毒在宿主细胞内增殖的示意图。

下面说法不合理的是（）A．图中+RNA有三方面功能B．物质M的合成场所是宿主细胞的核糖体C．患儿痊愈后若再次感染该病毒，相应的记忆细胞会迅速产生抗体消灭病毒D．假定肠道病毒基因+RNA含有1000个碱基，其中A和U占碱基总数的60%。

以病毒基因+RNA 为模板合成一条子代+RNA的过程共需要碱基G和C共800个4．下列关于免疫的叙述，正确的是（）A．吞噬细胞吞噬外来细菌，必须有抗体参与B．浆细胞与效应T细胞中的遗传信息有明显差异C．“先天性胸腺发育不全”的患者，细胞免疫有缺陷D．淋巴细胞都来自骨髓造血干细胞，都在骨髓中分化、发育成熟5．植物的生命活动受多种激素的调节，下图为去顶芽前后侧芽部位生长素和细胞分裂素的浓度变化及侧芽长度变化的曲线，下列叙述正确的是（）A．激素甲是生长素，激素乙是细胞分裂素B．生长素与细胞分裂素比值增加有利于侧芽的萌动C．激素甲、乙通过直接参与细胞内的代谢过程实现对生命活动的调节D．激素甲可直接用作农业除草剂，激素乙可直接用于延长蔬菜贮藏时间6．下列生物学实验中，均需要借助显微镜观察的是（）①检测生物组织中的蛋白质②观察DNA 和RNA 在细胞中的分布③观察叶肉细胞中的叶绿体④观察细胞中的线粒体⑤检测酵母菌无氧呼吸的产物⑥探究植物细胞的吸水和失水实验⑦观察根尖分生组织细胞的有丝分裂⑧低温诱导植物染色体数目的变化A．①②③④⑥⑦⑧B．②③④⑤⑥⑦C．②③④⑥⑦⑧D．①②③④⑤⑥⑦7．下列物质性质与应用对应关系正确的是（）A．浓硫酸具有吸水性，可用于干燥CO2B．工业上用焦炭还原二氧化硅制取晶体硅，同时生成二氧化碳C．氢氧化铁溶胶、NaCl溶液、淀粉溶液均具有丁达尔效应D．金属铁和铝为生活中常用的金属材料，因为铝的活泼性大于铁，所以通常状况下，铝比铁更容易锈蚀8．下列根据化学事实进行的相关推论，正确的是（）选项化学事实推论A 将SO2通入品红溶液中，溶液褪色SO2具有氧化性B 用硫酸酸化的H2O2溶液滴入Fe（NO3）2溶液中，溶液变黄色，氧化性：H2O2比Fe3＋强C 取某液体少许与NaOH溶液共热后，再滴加卤代烃中的卤原子是Cl原子AgNO3溶液，产生白色沉淀D 向溶液中滴加KSCN，无明显现象，再加氯水，看到溶液变为血红色说明原溶液中含有Fe2+9．设N A为阿伏加德罗常数的值，下列说法中正确的是（）A．H2O2溶液中加入MnO2可制得O2，产生2．24L（标况）O2，转移0．4N A个电子B．在52g苯乙烯（）中含有碳碳双键的个数是2N AC．100 mL 12 mol·L－1的浓HNO3与过量Cu反应转移电子的数目为0．6 N AD．标准状况下，11．2 L由CH4和C2H4组成的混合气体中含有氢原子的数目为2 N A10．25℃时，下列各组离子在指定溶液中一定能大量共存的是（）A．使酚酞变红色的溶液：Na＋、Ca2＋、NO3－、SO42－B．c（OH－）＝1×10－13 mol·L－1的溶液：I-、K＋、ClO－、SO42－C．使甲基橙变为红色的溶液中：Fe2+、K＋、Na＋、SO42－、NO3－D．在无色溶液中：MnO4-、Na＋、Mg2＋、NO3－、SO32－[11．化学反应中，有时存在物质的量多少不同，反应不同（或物质的浓度或反应温度、催化剂等反应条件不同，反应产物不同）的特殊情况。

2015年全国第三次模拟大联考【江苏卷】-掌门1对1英语试卷本试卷分五部分。

满分120分。

考试时间120分钟。

第Ⅰ卷（共85 分）第一部分：听力(共两节，满分20分)做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节（共5小题；每小题1分，满分5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. How does the woman usually feel when she is asked to sing?A. Excited.B. Relaxed.C. Worried.2. Why does the woman choose to stay in Beijing?A. Because Beijing is her hometown.B. Because she thinks Beijing is exciting.C. Because she has made some new friends there.3. What is the man?A. A singer.B. An employee.C. A student.4. What are the two speakers talking about?A. Their past summer vacation.B. Where to work after graduation.C. Their plans for the summer vacation.5. How does the man react to the woman‟s suggestion?A. He totally ignores it.B. He wants to have a try.C. He‟ll talk with his doctor first.第二节（共15 小题；每小题1分，满分15分）听下面5段对话或独白。

（第4题）AA 1B不CB 1不C 1不D 1不D不（第8题）绝密★启用前【学易大联考】2015年第三次全国大联考【江苏版】数学试卷考试时间：理150分钟，文120分钟；命题人：大联考命题中心第Ⅰ卷 必做题部分一、填空题：本大题共14个小题，每小题5分，共计70分，请把答案直接填写在答题卡相应的位置．．．．．．．．上． 1．已知集合{}1,2,4A =，{},4B a =，若{1,2,3,4}U AB ==，则UC B = .2．已知复数z 满足(),(,)a bi z b ai a b R -=+ ,则z 的模为 3．“0x >”是 “12x x+≥”的_______________条件．4．执行如图所示的伪代码，则输出的结果为 ．5．已知O 为∆ABC 的外心，2BM MC =，3AC =.若4AO AM ⋅=，则AB = .6．已知函数 224cos 3,0,()2,0x x f x x x x ⎧--≥⎪=⎨+<⎪⎩，则不等式 (())3f f x ≤的解集为_____.7．已知函数7425()()()()()3333f x x x x x =--++14,33x ⎛⎫⎛⎫∈ ⎪ ⎪⎝⎭⎝⎭，则函数()y f x =的值域为 .8. 如图，在长方体1111ABCD A B C D -中，AB =3 cm ，AD =2 cm ，1AA =1 cm ，则点1B 到面1ABD 的距离为 cm ．9．若锐角三角形三个内角的度数成等差数列，且最大边与最小边长度之比为m ，则m 的取值范围是 .10．已知直线39ax by +=经过点(1,3)P ，则411a b+-的取值范围为 . 11. 设1x 为曲线)0(1<-=x xy 与x y ln =公切线的一个切点横坐标，且10x <，则满足1m x ≥的最小整数m 值为 .1C BCMN1A1B 12．已知函数2014(),(,f x x ax b a b =-++为常数），若|()|f x 在[1,1]-上最小值为12，则20152a b +的值为 .13．在平面直角坐标系xOy 中，已知椭圆C :2212412x y+=,设00(,)R x y 是椭圆C 上的任一点，从原点O 向圆R ：()()22008x x y y -+-=作两条切线，分别交椭圆于点P ，Q .若直线OP ，OQ 的斜率存在，并记为1k ，2k ，则12_______.k k =14．已知P 点为圆1O 与圆2O 公共点，圆2221:()()O x a y b b -+-=，圆2222:()()O x c y d d -+-= ，若9,a cac b d==，则点P 与直线l ：34250x y --=上任意一点M 之间的距离的最小值为 .二、解答题：本大题共6小题，计90 分。