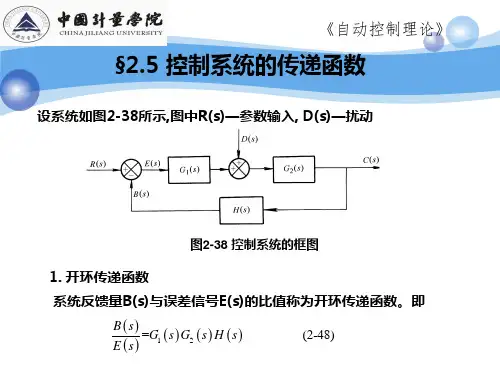
自动控制理论系统框图.docx

《自动控制理论 （夏德钤）》习题答案详解第二章2-1 试求图2-T-1所示RC 网络的传递函数。

(a)11111111+=+⋅=Cs R R CsR Cs R z ，22R z =，则传递函数为： 2121221212)()(R R Cs R R R Cs R R z z z s U s U i o +++=+= (b) 设流过1C 、2C 的电流分别为1I 、2I ，根据电路图列出电压方程：⎪⎪⎩⎪⎪⎨⎧=++=)(1)()]()([)(1)(2221111s I s C s U s I s I R s I sC s U o i 并且有)()1()(122211s I sC R s I s C += 联立三式可消去)(1s I 与)(2s I ，则传递函数为：1)(1111)()(222111221212211112++++=⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛++=s C R C R C R s C C R R R s C R s C s C R sC s U s U i o2-2 假设图2-T-2的运算放大器均为理想放大器，试写出以i u 为输入，o u 为输出的传递函数。

(a)由运算放大器虚短、虚断特性可知：dtduC dt du C R u i i 0+-=，0u u u i c -=， 对上式进行拉氏变换得到)()()(0s sU s sU RCs U i i +-= 故传递函数为RCsRCs s U s U i 1)()(0+=(b)由运放虚短、虚断特性有：022=-+--R u R u u dt du Cc c i c ，0210=+R u R u c ，联立两式消去c u 得到02220101=++⋅u R u R dt du R CR i 对该式进行拉氏变换得0)(2)(2)(20101=++s U R s U R s sU R CR i 故此传递函数为)4(4)()(10+-=RCs R R s U s U i (c)02/2/110=+-+R u R u u dt du Cc c c ，且21R uR u c i -=，联立两式可消去c u 得到 0222101=++⋅Ru R u dt du R CR ii 对该式进行拉氏变换得到0)(2)(2)(2011=++⋅s U Rs U R s sU R CR i i 故此传递函数为RCs R R s U s U i 4)4()()(110+-= 2-3 试求图2-T-3中以电枢电压a u 为输入量，以电动机的转角θ为输出量的微分方程式和传递函数。

自动控制理论第四版课后习题详细解答答案夏德钤翁贻方版集团标准化工作小组 #Q8QGGQT-GX8G08Q8-GNQGJ8-MHHGN#《自动控制理论 （夏德钤）》习题答案详解第二章2-1 试求图2-T-1所示RC 网络的传递函数。

(a)11111111+=+⋅=Cs R R CsR Cs R z ，22R z =，则传递函数为： (b) 设流过1C 、2C 的电流分别为1I 、2I ，根据电路图列出电压方程： 并且有联立三式可消去)(1s I 与)(2s I ，则传递函数为：2-2 假设图2-T-2的运算放大器均为理想放大器，试写出以i u 为输入，o u 为输出的传递函数。

(a)由运算放大器虚短、虚断特性可知：dtduC dt du C R u i i 0+-=，0u u u i c -=， 对上式进行拉氏变换得到 故传递函数为(b)由运放虚短、虚断特性有：022=-+--R u R u u dt du C c c i c ，0210=+R u R u c ，联立两式消去c u 得到 对该式进行拉氏变换得 故此传递函数为 (c)02/2/110=+-+R u R u u dt du Cc c c ，且21R uR u c i -=，联立两式可消去c u 得到 对该式进行拉氏变换得到 故此传递函数为2-3 试求图2-T-3中以电枢电压a u 为输入量，以电动机的转角θ为输出量的微分方程式和传递函数。

解：设激磁磁通f f i K =φ恒定2-4 一位置随动系统的原理图如图2-T-4所示。

电动机通过传动链带动负载及电位器的滑动触点一起移动，用电位器检测负载运动的位移，图中以c 表示电位器滑动触点的位置。

另一电位器用来给定负载运动的位移，此电位器的滑动触点的位置（图中以r 表示）即为该随动系统的参考输入。

两电位器滑动触点间的电压差e u 即是无惯性放大器（放大系数为a K ）的输入，放大器向直流电动机M 供电，电枢电压为u ，电流为I 。

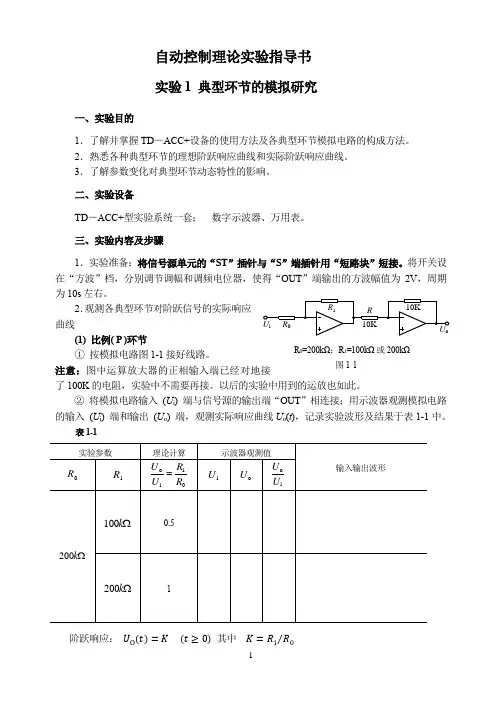
自动控制理论实验指导书实验1 典型环节的模拟研究一、实验目的1．了解并掌握TD －ACC+设备的使用方法及各典型环节模拟电路的构成方法。

2．熟悉各种典型环节的理想阶跃响应曲线和实际阶跃响应曲线。

3．了解参数变化对典型环节动态特性的影响。

二、实验设备TD －ACC+型实验系统一套；数字示波器、万用表。

三、实验内容及步骤1．实验准备：将信号源单元的“ST ”插针与“S ”端插针用“短路块”短接。

将开关设在“方波”档，分别调节调幅和调频电位器，使得“OUT ”端输出的方波幅值为2V ，周期为10s 左右。

2．观测各典型环节对阶跃信号的实际响应曲线 (1) 比例( P )环节① 按模拟电路图1-1接好线路。

注意：图中运算放大器的正相输入端已经对地接了100K 的电阻，实验中不需要再接。

以后的实验中用到的运放也如此。

② 将模拟电路输入 (U i ) 端与信号源的输出端“OUT ”相连接；用示波器观测模拟电路的输入 (U i ) 端和输出 (U o ) 端，观测实际响应曲线U o (t )，记录实验波形及结果于表1-1中。

表1-1阶跃响应： U O (t )=K (t ≥0) 其中 K =R 1R 0⁄实验参数理论计算示波器观测值输入输出波形0R 1Ro 1i 0U R U R =i U o Uo iU U Ωk 200Ωk 1000.5Ωk 2001R 0=200kΩ；R 1=100kΩ或200kΩ图1-1U i R 0R 1RR 10K 10K U o(2) 积分( I )环节①按图1-2接好线路。

② 将模拟电路输入 (U i ) 端与信号源的输出端“OUT ”相连接；用示波器观测模拟电路的输入 (U i ) 端和输出 (U o ) 端，观测实际响应曲线U o (t )，测量积分时间T ，记录实验波形及结果于表1-2中。

表1-2阶跃响应： o 01()U t t R C=(t ≥0) 注意：积分时间T 是指积分初始时间到输出值等于输入值时的时间。

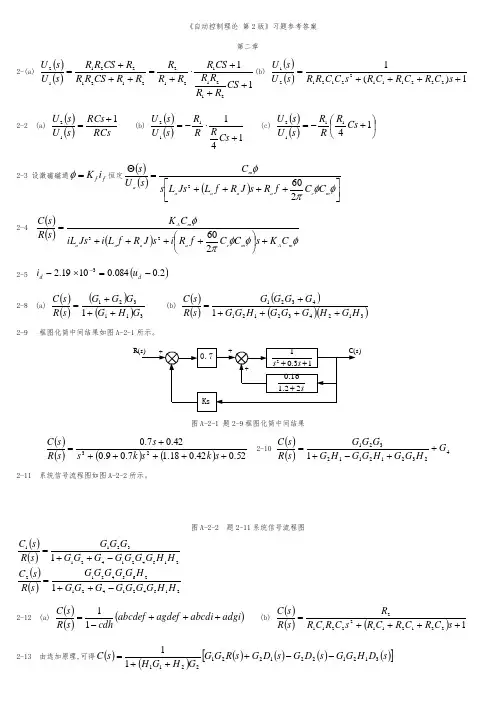
《自动控制理论 第2版》习题参考答案第二章2-(a)()()1121211212212122112+++⋅+=+++=CS R R R R CS R R R R R R CS R R R CS R R s U s U (b) ()()1)(12221112212121++++=s C R C R C R s C C R R s U s U 2-2 (a)()()RCs RCs s U s U 112+= (b) ()()141112+⋅-=Cs R R R s U s U (c) ()()⎪⎭⎫⎝⎛+-=141112Cs R R R s U s U2-3 设激磁磁通ff i K =φ恒定()()()⎥⎦⎤⎢⎣⎡++++=Θφφπφm e a a a a m a C C f R s J R f L Js L s C s U s 2602 2-4()()()φφφπφm A m e a a a a m A C K s C C f R i s J R f L i Js iL C K s R s C +⎪⎭⎫⎝⎛++++=260232-5 ()2.0084.01019.23-=⨯--d du i2-8 (a)()()()()3113211G H G G G G s R s C +++=(b)()()()()()31243212143211H G H G G G H G G G G G G s R s C +++++=2-9 框图化简中间结果如图A-2-1所示。

图A-2-1 题2-9框图化简中间结果()()()()52.042.018.17.09.042.07.023++++++=s k s k s s s R s C 2-10()()4232121123211G H G G H G G H G G G G s R s C ++-+=2-11 系统信号流程图如图A-2-2所示。

图A-2-2 题2-11系统信号流程图()()()()2154214212654212215421421321111H H G G G G G G G H G G G G G s R s C H H G G G G G G G G G G s R s C -++=-++=2-12 (a)()()()adgi abcdi agdef abcdef cdhs R s C +++-=11(b) ()()()1221211222112++++=s C R C R C R s C R C R R s R s C2-13 由选加原理,可得()()()()()()[]s D H G G s D G s D G s R G G G H G H s C3121221221221111--+++=第三章3-1 分三种情况讨论 (a) 当1>ζ时()()()()()⎥⎥⎦⎤⎢⎢⎣⎡-+----+-=-+-=---=⎪⎭⎫ ⎝⎛-+-⎪⎭⎫ ⎝⎛---221221222211112121,122ζζζζωζωζωζζωζζωζζωζζt t n n nn n n e e t t c s s (b) 当10<<ζ时()()()⎪⎪⎭⎫⎝⎛-----+-=---+---=-+-=---=---22222222222121121sin 1121sin 1211cos 221,1ζζζωζωζωζωζωζζωζωζωζωζζωζζζωζωζωarctg t et t e t et t c j s j s n tnnn t nn tnnn n n n n(c) 当1=ζ时设系统为单位反馈系统,有()()()()()2222nn n rs s s s R s c s R s E ωζωζω+++=-=系统对单位斜坡输入的稳态误差为 ()nn n n s srs s s s s s im e ωζωζωζω22212220=+++⋅⋅=→3-2 (1) 0,0,50===a v pK K K (2) 0,,==∞=a v p K K K K(3) 10,,K K K K a v p=∞=∞= (4) 0,200,==∞=a v p K K K K 3-3 首先求系统的给定误差传递函数()101.0)11.0()(11)()(2+++=+==Φs s s s s G s R s E s e误差系数可求得如下()()()0)101.0()12.0(20)101.0(2lim lim 1.0)101.0()12.0(10lim lim 0101.0)11.0(lim lim 322202202220012000=+++-++=Φ==+++=Φ==+++=Φ=→→→→→→s s s s s s ds d C s s s s ds d C s s s s s C s e s s es s e s(1) 0)(R t r =，此时有0)()(,)(0===t r t r R t r s s s ，于是稳态误差级数为()0)(0==t r C t e s sr ，0≥t (2) t R R t r 10)(+=，此时有0)(,)(,)(110==+=t r R t r t R R t r s s s ，于是稳态误差级数为()1101.0)()(R t rC t r C t e s s sr =+= ，0≥t ()⎪⎭⎫ ⎝⎛++-=-=-t et t c s ntnnn n 21222,1ωωωωω(3) 221021)(t R t R R t r ++=，此时有t R R t rt R t R R t r s s 212210)(,21)(+=++= ，2)(R t r s = ，于是稳态误差级数为 ())(1.0)(!2)()(21210t R R t r C t rC t r C t e s s s sr +=++= ，0≥t 3-4 首先求系统的给定误差传递函数()5001.0)11.0()(11)()(2+++=+==Φs s s s s G s R s E s e误差系数可求得如下()()()232220220222001200050098)5001.0()12.0(1000)5001.0(100lim lim 5001)5001.0()12.0(500lim lim 05001.0)11.0(lim lim =+++-++=Φ==+++=Φ==+++=Φ=→→→→→→s s s s s s ds d C s s s s ds d C s s s s s C s e s s es s e stt r t t rt t r s s s 5sin 25)(5cos 5)(5sin )(-===稳态误差级数为()[][][]tt tC t C C t e sr 5cos 1015sin 109.45cos 55sin 25224120 -⨯++⨯=-⨯+⎥⎦⎤⎢⎣⎡+⨯-=- 3-6 系统在单位斜坡输入下的稳态误差为 nsr e ωζ2=加入比例—微分环节后()()()()[]()()()()()()()()()()()()()()()nns sr nn nnnnna s sE im e s s R s R s s sa s s C s R s E s R s s as s R s G s G as s C s G s C as s R s C ωωζωζωωωζωζωω-===++-+=-=+++=++=-+=→21222111102222222可见取na ωζ2=，可使0=sre3-7 588.19,598.0==n ωζ3-8 ()()6442++=s s s s G3-9 按照条件（2）可写出系统的特征方程2)22()2())(22())(1)(1(232=+++++=+++=+++-+a s a s a s a s s s a s j s j s将上式与0)(1=+s G 比较，可得系统的开环传递函数[])22()2(2)(2a s a s s as G ++++=根据条件（1），可得aa e K sr v 2225.01+===解得1=a，于是由系统的开环传递函数为[]432)(2++=s s s s G3-10()()()())5.0,/1(,%28%,3.162)24.0,/12.2(,%299.7%,6.461========ζωζωs rad s t Ms rad s t M n s pn s p ()s ts153=)25.1,/4.0(,==ζωs rad n ，过阻尼系统，无超调。

第一章绪论1-1试比较开环控制系统和闭环控制系统的优缺点.解答：1开环系统(1)优点:结构简单，成本低，工作稳定。

用于系统输入信号及扰动作用能预先知道时，可得到满意的效果。

(2)缺点：不能自动调节被控量的偏差。

因此系统元器件参数变化，外来未知扰动存在时，控制精度差。

2闭环系统⑴优点：不管由于干扰或由于系统本身结构参数变化所引起的被控量偏离给定值，都会产生控制作用去清除此偏差，所以控制精度较高。

它是一种按偏差调节的控制系统。

在实际中应用广泛。

⑵缺点：主要缺点是被控量可能出现波动，严重时系统无法工作。

1-2什么叫反馈？为什么闭环控制系统常采用负反馈？试举例说明之。

解答：将系统输出信号引回输入端并对系统产生控制作用的控制方式叫反馈。

闭环控制系统常采用负反馈。

由1-1中的描述的闭环系统的优点所证明。

例如，一个温度控制系统通过热电阻(或热电偶)检测出当前炉子的温度，再与温度值相比较，去控制加热系统，以达到设定值。

1-3试判断下列微分方程所描述的系统属于何种类型(线性，非线性，定常，时变)？2 心$ +3 如+ 4(0 = 5 如+ 6临)(1)dt~ dt dt(2)y(0 = 2 + w(r)竺+ 2y(/) = 4如+ “⑴(3)dt dt⑴ + 2y(t) = u(t) sin cot(4)dt钞+W)響+ 2W)»)(5)dt~ dt(6) dt -y(t) = 2u(t) +3(7)":⑴ + 5 j*解答：(1)线性定常(4)线性时变(7)线性定常(2)非线性定常(5)非线性定常(3)线性时变(6)非线性定常1-4如图1-4是水位自动控制系统的示意图，图中QI, Q2分别为进水流量和出水流量。

控制的目的是保持水位为一定的高度。

试说明该系统的工作原理并画出其方框图。

解答：(1)方框图如下：给定水位实际水温_____ 浮子—►杠杆—> 阀门_►水箱 _______________________________ _____ (⑵工作原理：系统的控制是保持水箱水位高度不变。