自动控制理论课件
- 格式:ppt
- 大小:1.07 MB
- 文档页数:67







1.1 自动控制理论的定义1.2 自动控制系统的分类1.3 自动控制理论的应用领域二、数学基础2.1 线性代数基础2.2 微积分基础2.3 常微分方程2.4 拉普拉斯变换三、经典控制理论3.1 概述3.2 传递函数3.3 系统稳定性分析3.4 系统响应分析3.5 系统校正设计四、现代控制理论4.1 状态空间描述4.2 状态空间分析4.3 控制器设计4.4 观测器设计4.5 系统李雅普诺夫稳定性分析五、线性二次调节器5.2 性能指标5.3 调节器设计5.4 数字实现六、非线性控制系统6.1 非线性系统的特点6.2 非线性方程和方程组的求解6.3 非线性系统的分析和设计方法6.4 非线性控制系统的应用实例七、模糊控制系统7.1 模糊控制理论的基本概念7.2 模糊控制规则和推理方法7.3 模糊控制器的设计7.4 模糊控制系统的仿真和应用八、自适应控制系统8.1 自适应控制的基本概念8.2 自适应控制算法8.3 自适应控制系统的性能分析8.4 自适应控制的应用实例九、智能控制系统9.1 智能控制的基本概念9.2 人工神经网络在自动控制中的应用9.3 遗传算法在自动控制中的应用9.4 模糊神经网络在自动控制中的应用十、自动控制技术的应用10.1 工业自动化10.2 交通运输自动化10.3 生物医学工程自动化10.4 家居自动化六、非线性控制系统6.1 非线性系统的特点6.2 非线性方程和方程组的求解求解非线性方程和方程组通常需要使用数值方法,如牛顿法、弦截法和迭代法等。
6.3 非线性系统的分析和设计方法对于非线性系统,常用的分析方法有相平面分析、李雅普诺夫方法和描述函数法等。
设计方法包括反馈线性化和滑模控制等。
6.4 非线性控制系统的应用实例例如,臂的控制、电动汽车的稳定控制等。
七、模糊控制系统7.1 模糊控制理论的基本概念模糊控制是一种基于的控制方法,它通过模糊逻辑对系统的输入和输出进行处理,从而实现控制目的。

自动控制原理(全套课件)一、引言自动控制原理是自动化领域的一门重要学科,它主要研究如何利用各种控制方法,使系统在受到扰动时,能够自动地、准确地、快速地恢复到平衡状态。
本课件将详细介绍自动控制的基本概念、控制系统的类型、数学模型、稳定性分析、控制器设计等内容,帮助学员全面掌握自动控制原理的基本理论和方法。
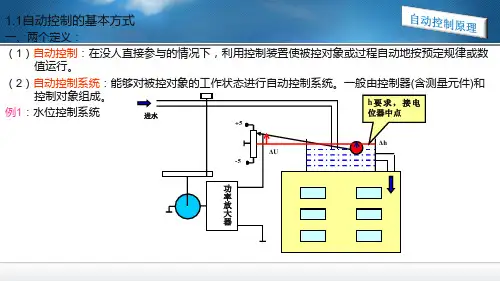
二、控制系统的基本概念1. 自动控制自动控制是指在没有人直接参与的情况下,利用控制器使被控对象按照预定规律运行的过程。
自动控制的核心在于控制器的设计,它能够根据被控对象的运行状态,自动地调整控制量,使系统达到预期的性能指标。
2. 控制系统控制系统是由被控对象、控制器、传感器和执行器等组成的闭环系统。
被控对象是指需要控制的物理过程或设备,控制器负责产生控制信号,传感器用于测量被控对象的运行状态,执行器则根据控制信号对被控对象进行操作。
三、控制系统的类型1. 按控制方式分类(1)开环控制系统:控制器不依赖于被控对象的运行状态,直接产生控制信号。
开环控制系统简单,但抗干扰能力较差。
(2)闭环控制系统:控制器依赖于被控对象的运行状态,通过反馈环节产生控制信号。
闭环控制系统抗干扰能力强,但设计复杂。
2. 按控制信号分类(1)连续控制系统:控制信号是连续变化的,如模拟控制系统。
(2)离散控制系统:控制信号是离散变化的,如数字控制系统。
四、控制系统的数学模型1. 微分方程模型微分方程模型是描述控制系统动态性能的一种数学模型,它反映了系统输入、输出之间的微分关系。
通过求解微分方程,可以得到系统在不同时刻的输出值。
2. 传递函数模型传递函数模型是描述控制系统稳态性能的一种数学模型,它反映了系统输入、输出之间的频率响应关系。
传递函数可以通过拉普拉斯变换得到,它是控制系统分析、设计的重要工具。
五、控制系统的稳定性分析1. 李雅普诺夫稳定性分析:通过构造李雅普诺夫函数,分析系统的稳定性。
2. 根轨迹分析:通过分析系统特征根的轨迹,判断系统的稳定性。