§4.7 周期信号的傅里叶变换

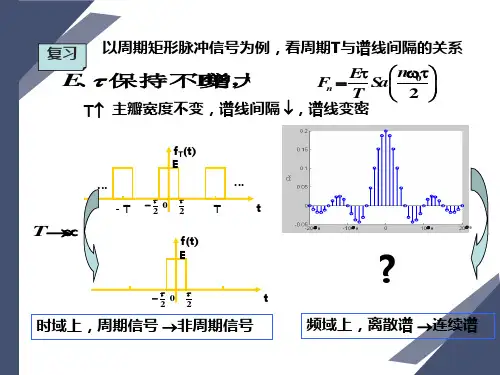
周期信号的傅里叶变换
周期信号的傅里叶变换与傅里叶级数有很大的关系，它与非周期信号的傅里叶不是一回事，非周期傅叶变换对不对用在周期信号上。

先做个铺垫：
虚指函数是一个周期函数，他的傅里叶变换可以从下面的开始考虑
由傅里叶级数可知，一个周期信号可以用
表示，即用一串虚指函数的加权表示。

那么由上式可知：虚指函数的傅里叶变换是02()πδωω-。

一个周期信号x （t ）的傅里叶变换是一个脉冲串，可用表示。

式
中表示的是，发生在第K 次谐波关系的的冲激函数的面积是加权的系数
的2pi 倍。

现在关键在于加权的系数的计算。

这里的就是傅里叶级数中的。

下面是傅里叶级数的表达式：
到此为止，可以计算周期信号的傅里叶变换了！
计算的时候注意，可以尽量先直接化成虚指函数，再根据虚指函数与脉冲这间的关系直接计算求得，如果不行，可以通过计算，再代入.
满足狄里赫利条件的周期信号都可以用傅里叶级数的形式表示，即虚指函数的加权；虚指函数的频谱为脉冲02()πδωω-，那么所有可以用傅里叶级数表示的周期信号的频谱都是脉冲串。

如正弦函数的频谱是在+wo 和-wo 处的脉冲。

常用傅里叶变换表傅里叶变换是信号处理和数学分析中常用的重要工具，可以将一个函数表示为一系列复指数函数的加权和，从而揭示了信号的频谱特性。

为了方便使用傅里叶变换，人们总结了一些常用的傅里叶变换表，以便在实际应用中快速查找和计算傅里叶变换。

以下是一些常用傅里叶变换表的示例：1. 时间域和频率域的关系当我们进行傅里叶变换时，需要将信号从时间域转换到频率域。

在时间域中，信号通常用函数的自变量表示，而在频率域中，信号则以频率为变量进行表示。

傅里叶变换表中可以列出频率的取值范围以及对应的时间域函数。

这样，我们就可以根据频率的取值范围，找到对应的时间域函数。

2. 傅里叶级数的表达傅里叶级数是傅里叶变换的一种特殊形式，适用于周期信号的分析。

傅里叶级数表包含了一系列关于系数和频率的信息，用于计算周期信号的频谱成分。

3. 傅里叶变换的基本性质傅里叶变换具有许多重要的性质和定理，包括线性性、平移性、尺度性等。

常用的傅里叶变换表可以列出这些性质和定理，并给出相应的公式和解释。

4. 常见函数的傅里叶变换表达式常见的函数，例如矩形函数、三角函数、指数函数等，它们的傅里叶变换具有一定的规律和特点。

傅里叶变换表可以提供这些常见函数的变换表达式，以便将它们与其他信号进行比较和分析。

5. 傅里叶变换的逆变换表达式傅里叶变换提供了将信号从时域转换到频域的方法，而逆傅里叶变换则将信号从频域转换回时域。

逆傅里叶变换表中包含了逆变换的表达式，可以用于将傅里叶变换后的频域信号还原为时域信号。

6. 傅里叶变换的性质推导除了使用表格给出傅里叶变换的常用形式，也可以通过推导的方式得到某些信号的傅里叶变换形式。

这种方式在一些特殊的情况下很有帮助，可以帮助理解和推广傅里叶变换的性质。

总结：常用傅里叶变换表是信号处理领域必备的工具之一。

通过使用傅里叶变换表，我们可以快速计算信号的频谱成分，深入理解信号的特性，加快信号处理的速度。

只要掌握了常见傅里叶变换表的使用方法和基本要点，我们就能更好地应用傅里叶变换进行信号分析和处理工作，提高工作效率。

信号傅里叶变换引言信号傅里叶变换是一种在信号处理中常用的数学工具，用于将一个信号从时域转换到频域。

通过傅里叶变换，我们可以将一个信号分解成若干不同频率分量的叠加，从而能够更加深入地理解信号的特性和结构。

本文将对信号傅里叶变换的原理、应用以及算法进行介绍，并对其进行详细解析。

信号傅里叶变换的原理信号傅里叶变换基于傅里叶级数展开的思想，将一个周期信号分解成一系列谐波分量的叠加。

而对于非周期信号，傅里叶变换则将其看作一个无穷长的周期信号，并将其分解成一系列频率连续的谐波分量的叠加。

傅里叶变换的核心思想是将一个信号转换成其频谱表示，即将信号在频域上的幅度和相位信息提取出来。

通过傅里叶变换，我们可以得到信号在不同频率上的能量分布情况，进而对信号进行分析和处理。

信号傅里叶变换的数学表达式对于一个信号f(t)，其傅里叶变换可以表示为：F(ω)=∫f∞−∞(t)e−jωt dt其中，F(ω)表示信号f(t)在频率为ω上的复振幅。

可以看出，傅里叶变换将信号f(t)从时域表示转换到频域表示。

逆傅里叶变换则将频域表示的信号恢复到时域，可以表示为：f(t)=12π∫F∞−∞(ω)e jωt dω信号傅里叶变换的应用信号傅里叶变换在信号处理领域有着广泛的应用。

以下是几个常见的应用场景：频谱分析频谱分析是傅里叶变换的主要应用之一。

通过对信号进行傅里叶变换，我们可以得到信号在频域上的能量分布情况，从而分析信号中不同频率分量的贡献程度。

频谱分析对于音频处理、图像处理等领域具有重要意义。

滤波器设计傅里叶变换可以用于滤波器的设计。

通过在频域上对信号进行滤波操作，我们可以选择性地增强或抑制信号中的某些频率分量，从而达到滤波的效果。

傅里叶变换为滤波器设计提供了有效的理论和工具。

图像处理信号傅里叶变换在图像处理中有着广泛的应用。

通过将图像进行傅里叶变换，我们可以提取图像的频域特征，进行频域滤波、图像增强、图像压缩等操作。

图像傅里叶变换也常用于图像压缩编码和图像识别等领域。