【步步高】2016高考数学大一轮复习 13.2直接证明与间接证明试题 理 苏教版
- 格式:doc
- 大小:54.00 KB
- 文档页数:4

第六节直接证明与间接证明基础回顾K一、直接证明1.综合法:从题设的已知条件出发,运用一系列有关已确定真实的命题作为推理的依据,逐步推演而得到要证明的结论,这种证明方法叫做综合法.综合法的推理方向是由已知到求证,表现为由因索果,综合法的解题步骤用符号表示是:P0(已知)⇒P1⇒P2⇒…⇒P n(结论).特点:由因导果,因此综合法又叫顺推法.2.分析法:分析法的推理方向是由结论到题设,论证中步步寻求使其成立的充分条件,如此逐步归结到已知的条件和已经成立的事实,从而使命题得证,表现为执果索因,分析法的证题步骤用符号表示为B(结论)⇐B1⇐B2⇐…⇐B n⇐A(已知).特点:执果索因,因此分析法又叫逆推法或执果索因法.二、间接证明假设原命题的结论不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立.这样的证明方法叫反证法.反证法是一种间接证明的方法.1.反证法的解题步骤:否定结论—推演过程中引出矛盾—肯定结论.2.反证法的理论依据是:原命题为真,则它的逆否命题为真,在直接证明有困难时,就可以转化为证明它的逆否命题成立.3.反证法证明一个命题常采用以下步骤:(1)假定命题的结论不成立;(2)进行推理,在推理中出现下列情况之一:与已知条件矛盾;与公理或定理矛盾;(3)由于上述矛盾的出现,可以断言,原来的假定“结论不成立”是错误的;(4)肯定原来命题的结论是正确的,即“反设—归谬—结论”.4.一般情况下,有如下几种情况的证明题目常常采用反证法:第一,问题共有n种情况,现要证明其中的1种情况成立时,可以想到用反证法把其他的n-1种情况都排除,从而肯定这种情况成立;第二,命题是以否定命题的形式叙述的;第三,命题用“至少”“至多”的字样叙述的;第四,当命题成立非常明显,而要直接证明所用的理论太少,且不容易说明,而其逆命题又是非常容易证明的.基础自测1.设t=a+2b,s=a+b2+1,则下列关于t和s的大小关系中正确的是(D)A.t>s B.t≥sC.t<s D.t≤s解析:因为s-t=a+b2+1-a-2b=(b-1)2≥0,所以s≥t.2.对任意的锐角α,β,下列不等式成立的是(D ) A .sin(α+β)>sin α+sin β B .cos(α+β)>cos α+cos β C .cos(α+β)<sin α+sin β D .cos(α+β)<cos α+cos β3.定义运算法则如下:a⊕b=a 12+b 13,a ⊗b =lg a 2-lg b 12.若M =214⊕1258,N =2⊗125,则M +N =5.解析:由定义运算法则可知,M =214⊕1258=94+ 31258=32+52=4, N =2⊗125=lg(2)2-lg ⎝ ⎛⎭⎪⎫12512=lg 2+lg 5=1,∴M +N =5.4.(2013·保定模拟)若P =a +a +7,Q =a +3+a +4,a ≥0,则P 、Q 的大小关系是P<Q .解析:分析法,要证P<Q ,需证P 2<Q 2即可.高考方向1.对本节内容的考查,一般贯穿在对其他知识的考查中,主要涉及综合法、反证法等证明方法,多以选择题和解答题为主,难度中等.2.分析法作为一种证明方法,较少单独考查,但这种方法可以用来寻找解题思路.品味高考1.(2014·湖南卷)如图,四棱柱ABCDA 1B 1C 1D 1的所有棱长都相等,AC ∩BD =O ,A 1C 1∩B 1D 1=O 1,四边形ACC 1A 1和四边形BDD 1B 1均为矩形.(1)证明:O 1O ⊥底面ABCD ;(2)若∠CBA=60°,求二面角C 1OB 1D 的余弦值. (1)证明:因为四边形ACC 1A 1为矩形,所以CC 1⊥AC. 同理DD 1⊥BD.因为CC 1∥DD 1,所以CC 1⊥BD. 而AC∩BD=O ,因此CC 1⊥底面ABCD. 由题设知,O 1O ∥C 1C ,故O 1O ⊥底面ABCD.(2)解析:如图,过O 1作O 1H ⊥OB 1于点H ,连接HC 1.由(1)知,O 1O ⊥底面ABCD ,所以O 1O ⊥底面A 1B 1C 1D 1,于是O 1O ⊥A 1C 1.又因为四棱柱ABCD -A 1B 1C 1D 1的所有棱长都相等, 所以四边形A 1B 1C 1D 1是菱形,因此A 1C 1⊥B 1D 1,从而A 1C 1⊥平面BDD 1B 1, 所以A 1C 1⊥OB 1,于是OB 1⊥平面O 1HC 1, 进而OB 1⊥C 1H.故∠C 1HO 1是二面角C 1OB 1D 的平面角.不妨设AB =2.因为∠CBA=60°,所以OB =3,OC =1, OB 1=7.在Rt △OO 1B 1中,易知O 1H =OO 1·O 1B 1OB 1=237. 而O 1C 1=1,于是C 1H =O 1C 21+O 1H 2=1+127=197. 故cos ∠C 1HO 1=O 1HC 1H=237197=25719.即二面角C 1OB 1D 的余弦值为25719. 2.(2013·江苏卷)已知向量a =(cos α,sin α),b =(cos β,sin β),0<β<α<π.(1)若|a -b|=2,求证:a⊥b;(2)设c =(0,1),若a +b =c ,求α,β的值.(1)证明:由|a -b|=2,即(cos α-cos β)2+(sin α-sin β)2=2,整理得cos αcos β+sin αsin β=0,即a·b=0,因此a⊥b.(2)解析:由已知条件⎩⎪⎨⎪⎧cos α+cos β=0,sin α+sin β=1,又0<β<α<π,cos β=-cos α=cos(π-α),则β=π-α, sin α+sin(π-α)=1,所以sin α=12,得α=π6或α=5π6,当α=π6时,β=5π6(舍去),当α=5π6时,β=π6.高考测验1.如图,三棱柱ABCA 1B 1C 1中,侧棱与底面垂直,AB ⊥AC ,AB =AC =AA 1=2,点M ,N 分别为A 1B 和B 1C 1的中点.(1)证明:MN∥平面A 1ACC 1; (2)求二面角NMCA 的正弦值.(1)证明:如图所示,取A 1B 1的中点P ,连接MP ,NP.又因为点M ,N 分别为A 1B 和B 1C 1的中点,所以NP ∥A 1C 1,MP ∥B 1B ,因为NP ⊂平面MNP ,A 1C 1⊄平面MNP ,所以NP∥平面A 1ACC 1;同理MP∥平面A 1ACC 1;又MP∩NP=P ,所以平面MNP∥平面A 1ACC 1; 所以MN∥平面A 1ACC 1;(2)解析:侧棱与底面垂直可得A 1A ⊥AB ,A 1A ⊥AC ,及AB ⊥AC ,可建立如图所示的空间直角坐标系.则A(0,0,0),B(2,0,0),C(0,2,0),A 1(0,0,2),B 1(2,0,2),C 1(0,2,2),N(1,1,2),M(1,0,1).所以MC →=(-1,2,-1),CN →=(1,-1,2),AC →=(0,2,0). 设平面ACM 的法向量为n 1=(x 1,y 1,z 1),则⎩⎪⎨⎪⎧n 1·AC →=2y 1=0,n 1·MC →=-x 1+2y 1-z 1=0,令x 1=1,则z 1=-1,所以n 1=(1,0,-1).设平面NCM 的法向量为n 2=(x 2,y 2,z 2), 则⎩⎪⎨⎪⎧n 2·MC →=-x 2+2y 2-z 2=0,n 2·CN →=x 2-y 2+2z 2=0,令x 2=3,则y 2=1,z 2=-1.所以n 2=(3,1,-1). 所以cos 〈n 1,n 2〉=|n 1·n 2||n 1||n 2|=3+12×32+12+(-1)2=22211. 设二面角NMCA 为θ,则 sin θ=1-cos 2〈n 1,n 2〉=1-⎝ ⎛⎭⎪⎫222112=3311. 故二面角NMCA 的正弦值为3311. 2.设数列{a n }的前n 项和为S n ,且S 2n -2S n -a n ·S n +1=0,n ∈N *. (1)求S n 与S n -1(n≥2)的关系式,并证明数列⎩⎨⎧⎭⎬⎫1S n -1是等差数列; (2)设b n =a n ·S n ,数列{b n }的前n 项和为T n ,求证:n 2(n +2)<T n <23.(1)解析:当n =1时,由已知得a 21-2a 1-a 21+1=0, 解得a 1=12.由题设S 2n -2S n -a n ·S n +1=0,当n≥2时,将a n =S n -S n -1代入上式, 得S n ·S n -1-2S n +1=0. ∴S n =12-S n -1,∴1S n -1-1S n -1-1=-1.∴⎩⎨⎧⎭⎬⎫1S n -1是首项为1S 1-1=-2,公差为-1的等差数列.(2)证明:由(1)知1S n -1=-2+(n -1)·(-1)=-n -1,∴S n =n n +1,n ∈N *. ∴a n =S n -S n -1=1n (n +1)(n≥2),n =1时也符合该式,∴a n =1n (n +1),n ∈N *.∴b n =a n ·S n =1(n +1)2.∴T n =b 1+b 2+…+b n =122+132+142+…+1(n +1)2.∴122+132+142+…+1(n +1)2>12×3+13×4+14×5+…+1(n +1)(n +2)=12-1n +2=n2(n +2).而b n =1(n +1)2<1(n +1)2-14=1(n +12)(n +32)=1n +12-1n +32, ∴122+132+142+…+1(n +1)2<11+12-11+32+12+12-12+32+…+1n +12-1n +32 =23-22n +3<23. ∴n 2(n +2)<T n <23得证.课时作业1.否定“自然数a 、b 、c 中恰有一个偶数”时正确反设为(D ) A .a 、b 、c 都是奇数 B .a 、b 、c 都是偶数C .a 、b 、c 中至少有两个偶数D .a 、b 、c 中或都是奇数或至少有两个偶数解析:自然数a 、b 、c 中奇数、偶数的可能情况有全为奇数,恰有一个偶数,恰有两个偶数,全为偶数.故选D.2.下列条件:①ab>0,②ab<0,③a>0,b>0,④a<0,b<0.其中能使b a +ab ≥2成立的条件有(C )A .1个B .2个C .3个D .4个解析:要使b a +a b ≥2,只需b a >0,ab >0,即a ,b 不为0且同号即可,∴①③④满足.故选C.3.已知0<b <a <14,则a -b ,a -b ,a -b 的大小顺序是(B )A.a -b >a -b >a - bB.a -b >a -b >a -bC.a -b >a -b >a -b D .a -b >a -b >a - b解析:平方后转化为作差分解因式或特殊值代入.4.规定记号“表示一种运算,即a b =ab +a +b 2(a ,b 为正实数),若1k =3,则k =(B )A .-2B .1C .-2 或1D .2解析:根据运算有1·k+1+k 2=3,k ∈R +,即k 2+k -2=0,解得k =1或k =-2(舍去).∴k=1.故选B.5.设A =1210+1210+1+…+1211-1,则下列结论正确的是(B )A .A >1B .A <1C .A ≥1D .A ≤1解析:放缩法对每一项放大范围,A =1210+1210+1+…+1210+1 023<1210+1210+1210+…+12101 024个=1.6.用反证法证明“如果a >b ,那么3a >3b ”7.函数y =log a (x +3)-1(a>0且a≠1)的图象恒过定点A ,若点A 在直线mx +ny +1=0上,其中m ,n>0,则1m +2n的最小值为8.解析:函数y =log a (x +3)-1(a>0且a≠1)的图象恒过定点A(-2,-1),则(-2)·m+(-1)·n+1=0,即2m +n =1.因为m ,n>0,所以1m +2n =⎝ ⎛⎭⎪⎫1m +2n ·(2m +n)=4+n m +4mn ≥4+2n m ·4m n (当且仅当n m =4mn时,等号成立)=8. 8.已知函数f(x)=ax +2a +1,当x∈[-1,1]时,f(x)有正值也有负值,则实数a 的取值范围为⎝⎛⎭⎪⎫-1,-13.解析:由题意得f(x)=ax +2a +1为斜率不为0的直线,由单调性知f(1)·f(-1)<0,∴(a +2a +1)·(2a-a +1)<0. ∴-1<a<-13.9.已知a>0,1b -1a >1,求证:1+a>11-b .证明:由已知1b -1a >1及a>0可知0<b<1,要证1+a>11-b ,只需证1+a ·1-b>1,只需证1+a -b -ab>1, 只需证a -b -ab>0即a -bab>1,即1b -1a>1,这是已知条件,所以原不等式得证. 10.已知O 为坐标原点,过P(2,0)且斜率为k 的直线交抛物线y 2=2x 于M(x 1,y 1),N(x 2,y 2)两点.(1)写出直线l 的方程; (2)求x 1x 2,y 1y 2的值; (3)求证:OM⊥ON.(1)解析:∵直线l 过点P(2,0)且斜线为k , 则直线l 的方程为y =k(x -2).(2)解析:∵直线l 与抛物线相交于M(x 1,y 1),N(x 2,y 2),且l 的方程为y =k(x -2),联立方程组⎩⎪⎨⎪⎧y =k (x -2),y 2=2x ⇒k 2x 2-(4k 2+2)x +4k 2=0. 根据韦达定理得x 1x 2=4k2k2=4.又∵M、N 都在y 2=2x 上, ∴y 21=2x 1,y 22=2x 2, ∴y 21·y 22=4x 1x 2, ∴y 1y 2=±4.又∵M、N 不可能都在x 轴上方或下方, ∴y 1y 2<0.∴y 1y 2=4(舍去), ∴y 1y 2=-4.(3)证明:M 、N 为y 2=2x 上的两点. 直线OM 的斜率k OM =y 1-0x 1-0=y 1x 1.直线ON 的斜率k ON =y 2-0x 2-0=y 2x 2.∴k OM ·k ON =y 1y 2x 1x 2.又∵y 1y 2=-4,x 1x 2=4, ∴k OM ·k ON =-1, ∴OM ⊥ON.11.如图,已知直线a 与b 不共面,直线c∩a=M ,直线b∩c=N ,又a∩面α=A ,b ∩α=B ,c ∩α=C.求证:A 、B 、C 三点不共线.证明:假设A 、B 、C 三点共线l , ∵A 、B 、C∈a,∴l⊂a.∵l∩c=C,∴c与l可确定一个平面β.∵c∩a=M,∴M∈β,又A∈l,∴a⊂β,同理b⊂β.∴a、b共面,与a、b异面矛盾.∴A、B、C三点不共线.。

2019高考数学大一轮复习 13.2直接证明与间接证明教师用书理苏教版1.直接证明(1)综合法①定义:从已知条件出发,以已知的定义、公理、定理为依据,逐步下推,直到推出要证明的结论为止,这种证明方法常称为综合法.②框图表示:已知条件⇒…⇒…⇒结论③思维过程:由因导果.(2)分析法①定义:从问题的结论出发,追溯导致结论成立的条件,逐步上溯,直到使结论成立的条件和已知条件或已知事实吻合为止.这种证明方法常称为分析法.②框图表示:结论⇐…⇐…⇐已知条件③思维过程:执果索因.2.间接证明反证法定义要证明某一结论Q是正确的,但不直接证明,而是先去假设Q不成立(即Q的反面非Q是正确的),经过正确的推理,最后得出矛盾,因此说明假设非Q是错误的,从而断定结论Q是正确的,这种证明方法叫做反证法.证明步骤(1)反证——假设命题的结论不成立,即假定原结论的反面为真;(2)归谬——从反设和已知条件出发,经过一系列正确的逻辑推理,得出矛盾结果;(3)存真——由矛盾结果,断定反设不真,从而肯定原结论成立.适用范围(1)否定性命题;(2)命题的结论中出现“至少”“至多”“唯一”等词语的;(3)当命题成立非常明显,而要直接证明所用的理论太少,且不容易说明,而其逆否命题又是非常容易证明的;(4)要讨论的情况很复杂,而反面情况很少.【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”) (1)综合法是直接证明,分析法是间接证明.( × )(2)分析法是从要证明的结论出发,逐步寻找使结论成立的充要条件.( × ) (3)用反证法证明结论“a >b ”时,应假设“a <b ”.( × ) (4)反证法是指将结论和条件同时否定,推出矛盾.( × )(5)在解决问题时,常常用分析法寻找解题的思路与方法,再用综合法展现解决问题的过程.( √ )(6)证明不等式2+7<3+6最合适的方法是分析法.( √ )1.p =ab +cd ,q =ma +nc ·b m +dn(m ,n ,a ,b ,c ,d 均为正数),则p ,q 的大小为关系为________. 答案 p ≤q 解析 q =ab +mad n +nbcm+cd ≥ab +2abcd +cd =ab +cd =p .2.要证a 2+b 2-1-a 2b 2≤0只要证明________. ①2ab -1-a 2b 2≤0; ②a 2+b 2-1-a 4+b 42≤0;③a +b22-1-a 2b 2≤0;④(a 2-1)(b 2-1)≥0. 答案 ④解析 a 2+b 2-1-a 2b 2≤0⇔(a 2-1)(b 2-1)≥0.3.若a ,b ,c 为实数,且a <b <0,则下列命题正确的是________. ①ac 2<bc 2 ②a 2>ab >b 2③1a <1b④b a >a b答案 ②解析 a 2-ab =a (a -b ), ∵a <b <0,∴a -b <0,∴a 2-ab >0, ∴a 2>ab .(1)又ab -b 2=b (a -b )>0,∴ab >b 2,(2) 由(1)(2)得a 2>ab >b 2.4.如果a a+b b>a b+b a,则a、b应满足的条件是__________________.答案a≥0,b≥0且a≠b解析∵a a+b b-(a b+b a)=a(a-b)+b(b-a)=(a-b)(a-b)=(a-b)2(a+b).∴当a≥0,b≥0且a≠b时,(a-b)2(a+b)>0.故a a+b b>a b+b a成立的条件是a≥0,b≥0且a≠b.题型一综合法的应用例1 对于定义域为[0,1]的函数f(x),如果同时满足:①对任意的x∈[0,1],总有f(x)≥0;②f(1)=1;③若x1≥0,x2≥0,x1+x2≤1,都有f(x1+x2)≥f(x1)+f(x2)成立,则称函数f(x)为理想函数.(1)若函数f(x)为理想函数,证明:f(0)=0;(2)试判断函数f(x)=2x(x∈[0,1]),f(x)=x2(x∈[0,1]),f(x)=x(x∈[0,1])是不是理想函数.思维点拨(1)取特殊值代入计算即可证明;(2)对照新定义中的3个条件,逐一代入验证,只有满足所有条件,才能得出“是理想函数”的结论,否则得出“不是理想函数”的结论.(1)证明取x1=x2=0,则x1+x2=0≤1,∴f(0+0)≥f(0)+f(0),∴f(0)≤0.又对任意的x∈[0,1],总有f(x)≥0,∴f(0)≥0.于是f(0)=0.(2)解对于f(x)=2x,x∈[0,1],f(1)=2不满足新定义中的条件②,∴f(x)=2x,(x∈[0,1])不是理想函数.对于f(x)=x2,x∈[0,1],显然f(x)≥0,且f(1)=1.任意的x1,x2∈[0,1],x1+x2≤1,f(x1+x2)-f(x1)-f(x2)=(x1+x2)2-x21-x22=2x1x2≥0,即f (x 1)+f (x 2)≤f (x 1+x 2). ∴f (x )=x 2(x ∈[0,1])是理想函数.对于f (x )=x ,x ∈[0,1],显然满足条件①②. 对任意的x 1,x 2∈[0,1],x 1+x 2≤1,有f 2(x 1+x 2)-[f (x 1)+f (x 2)]2=(x 1+x 2)-(x 1+2x 1x 2+x 2)=-2x 1x 2≤0, 即f 2(x 1+x 2)≤[f (x 1)+f (x 2)]2.∴f (x 1+x 2)≤f (x 1)+f (x 2),不满足条件③. ∴f (x )=x (x ∈[0,1])不是理想函数. 综上,f (x )=x 2(x ∈[0,1])是理想函数,f (x )=2x (x ∈[0,1])与f (x )=x (x ∈[0,1])不是理想函数.思维升华 (1)综合法是“由因导果”的证明方法,它是一种从已知到未知(从题设到结论)的逻辑推理方法,即从题设中的已知条件或已证的真实判断(命题)出发,经过一系列中间推理,最后导出所要求证结论的真实性. (2)综合法的逻辑依据是三段论式的演绎推理.(2013·课标全国Ⅱ)设a 、b 、c 均为正数,且a +b +c =1,证明:(1)ab +bc +ac ≤13;(2)a 2b +b 2c +c2a≥1.证明 (1)由a 2+b 2≥2ab ,b 2+c 2≥2bc ,c 2+a 2≥2ac 得a 2+b 2+c 2≥ab +bc +ca .由题设得(a +b +c )2=1, 即a 2+b 2+c 2+2ab +2bc +2ca =1.所以3(ab +bc +ca )≤1,即ab +bc +ca ≤13.(2)因为a 2b +b ≥2a ,b 2c +c ≥2b ,c 2a +a ≥2c ,故a 2b +b 2c +c 2a +(a +b +c )≥2(a +b +c ), 即a 2b +b 2c +c 2a ≥a +b +c .所以a 2b +b 2c +c 2a≥1. 题型二 分析法的应用 例2 已知a >0,求证a 2+1a 2-2≥a +1a-2.思维点拨 用分析法,移项,平方,化简. 证明 要证a 2+1a 2-2≥a +1a-2,只需要证a 2+1a 2+2≥a +1a+ 2.∵a >0,故只需要证( a 2+1a 2+2)2≥(a +1a+2)2,即a 2+1a2+4a 2+1a 2+4≥a 2+2+1a 2+22(a +1a )+2,从而只需要证2a 2+1a 2≥2(a +1a), 只需要证4(a 2+1a2)≥2(a 2+2+1a2),即a 2+1a2≥2,而上述不等式显然成立,故原不等式成立.思维升华 (1)逆向思考是用分析法证题的主要思想,通过反推,逐步寻找使结论成立的充分条件.正确把握转化方向是使问题顺利获解的关键.(2)证明较复杂的问题时,可以采用两头凑的办法,即通过分析法找出某个与结论等价(或充分)的中间结论,然后通过综合法证明这个中间结论,从而使原命题得证.已知a ,b ∈(0,+∞),求证:1333()a b + <1332()a b +.证明 因为a ,b ∈(0,+∞),所以要证原不等式成立, 只需证[1333()a b +]6<[1332()a b +]6, 即证(a 3+b 3)2<(a 2+b 2)3,即证a 6+2a 3b 3+b 6<a 6+3a 4b 2+3a 2b 4+b 6, 只需证2a 3b 3<3a 4b 2+3a 2b 4. 因为a ,b ∈(0,+∞), 所以即证2ab <3(a 2+b 2).而a 2+b 2≥2ab,3(a 2+b 2)≥6ab >2ab 成立, 以上步骤步步可逆, 所以1333()a b +<1332()a b +. 题型三 反证法的应用例3 已知数列{a n }的前n 项和为S n ,且满足a n +S n =2. (1)求数列{a n }的通项公式;(2)求证:数列{a n }中不存在三项按原来顺序成等差数列.思维点拨 证明(2)用反证法,假设存在三项,符合条件推出矛盾. (1)解 当n =1时,a 1+S 1=2a 1=2,则a 1=1. 又a n +S n =2,所以a n +1+S n +1=2,两式相减得a n +1=12a n ,所以{a n }是首项为1,公比为12的等比数列,所以a n =12n -1.(2)证明 反证法:假设存在三项按原来顺序成等差数列,记为a p +1,a q +1,a r +1(p <q <r ,且p ,q ,r ∈N *),则2·12q =12p +12r ,所以2·2r -q =2r -p+1.(*)又因为p <q <r ,所以r -q ,r -p ∈N *.所以(*)式左边是偶数,右边是奇数,等式不成立. 所以假设不成立,原命题得证.思维升华 (1)当一个命题的结论是以“至多”“至少”“唯一”或以否定形式出现时,可用反证法来证,反证法关键是在正确的推理下得出矛盾,矛盾可以是与已知条件矛盾,与假设矛盾,与定义、公理、定理矛盾,与事实矛盾等.(2)用反证法证明不等式要把握三点:①必须否定结论;②必须从否定结论进行推理;③推导出的矛盾必须是明显的.等差数列{a n }的前n 项和为S n ,a 1=1+2,S 3=9+3 2.(1)求数列{a n }的通项a n 与前n 项和S n ;(2)设b n =S nn(n ∈N *),求证:数列{b n }中任意不同的三项都不可能成为等比数列.(1)解 由已知得⎩⎨⎧a 1=2+1,3a 1+3d =9+32,∴d =2,故a n =2n -1+2,S n =n (n +2). (2)证明 由(1)得b n =S n n=n + 2.假设数列{b n }中存在三项b p ,b q ,b r (p ,q ,r ∈N *,且互不相等)成等比数列,则b 2q =b p b r , 即(q +2)2=(p +2)(r +2). ∴(q 2-pr )+2(2q -p -r )=0.∵p ,q ,r ∈N *,∴⎩⎪⎨⎪⎧q 2-pr =0,2q -p -r =0.∴(p +r2)2=pr ,即(p -r )2=0.∴p =r ,与p ≠r 矛盾.∴假设不成立,即数列{b n }中任意不同的三项都不可能成等比数列.放缩有“度”,巧证不等式典例:(14分)已知数列{x n }满足x 1=12,x n +1=2x n x 2n +1,求证:0<x n +1-x n <2+18.思维点拨 先证0<x n <1,再求x n +1-x n 的表达式,利用不等式放缩得出结论. 规范解答证明 由条件可知数列{x n }的各项均为正数, 故由基本不等式,得x n +1=2x n x 2n +1≤2x n2x n =1,[2分] 若x n +1=1,则x n =1, 这与已知条件x 1=12矛盾.所以0<x n <1,[6分]从而x n +1-x n =2x n x 2n +1-x n =x n ·1-x 2n1+x 2n=x n (1-x n )·1+x n1+x 2n=x n (1-x n )·11+x n +21+x n-2, 其中0<x n (1-x n )≤14,1+x n +21+x n ≥22,[12分]因上述两个不等式中等号不可能同时成立, 故0<x n +1-x n <14·122-2=2+18.[14分]温馨提醒 (1)所谓放缩法就是利用不等式的传递性,根据证题目标进行合情合理的放大或缩小,在使用放缩法证题时要注意放和缩的“度”,否则就不能同向传递了,此法既可以单独用来证明不等式,也可以是其他方法证题时的一个重要步骤.(2)本题技巧性较强,经过了两次放缩,关键是放缩后的式子要尽可能地接近原式,减小放缩度,以避免运算上的麻烦.第一次是利用基本不等式,将x n +1-x n 转化为常数,根据已知验证可判定出0<x n <1;第二次放缩法是证明不等式经常利用的方法,多采用添项或去项,分子、分母扩大或缩小,应用基本不等式进行放缩,放缩时要注意放缩的方向保持一致.在此步骤中,因两个等式中的等号不可能同时成立,所以两式相乘后不取等号,这是易错之处,必须加以警惕.方法与技巧1.分析法的特点:从未知看需知,逐步靠拢已知.2.综合法的特点:从已知看可知,逐步推出未知.3.分析法和综合法各有优缺点.分析法思考起来比较自然,容易寻找到解题的思路和方法,缺点是思路逆行,叙述较繁;综合法从条件推出结论,较简捷地解决问题,但不便于思考.实际证题时常常两法兼用,先用分析法探索证明途径,然后再用综合法叙述出来.失误与防范1.用分析法证明时,要注意书写格式的规范性,常常用“要证(欲证)……”“即证……”“只需证……”等,逐步分析,直至一个明显成立的结论.2.利用反证法证明数学问题时,要假设结论错误,并用假设的命题进行推理,如果没有用假设的命题推理而推出矛盾结果,其推理过程是错误的.A组专项基础训练(时间:40分钟)1.已知m>1,a=m+1-m,b=m-m-1,则a,b的大小关系为________.答案a<b解析∵a=m+1-m=1m+1+m,b=m-m-1=1m+m-1.而m+1+m>m+m-1,∴1m+1+m<1m+m-1,即a<b.2.若P=a+a+7,Q=a+3+a+4(a≥0),则P,Q的大小关系是________.答案P<Q解析∵P2=2a+7+2a·a+7=2a+7+2a2+7a,Q2=2a+7+2a+3·a+4=2a+7+2a2+7a+12,∴P2<Q2,∴P<Q.3.若a>0,b>0,a+b=2,则下列不等式对一切满足条件的a,b恒成立的是________(写出所有正确命题的编号).①ab ≤1;②a +b ≤2;③a 2+b 2≥2;④1a +1b≥2.答案 ①③④ 解析 ①ab ≤(a +b2)2=1,成立.②欲证a +b ≤2,即证a +b +2ab ≤2,即2ab ≤0,显然不成立. ③欲证a 2+b 2=(a +b )2-2ab ≥2,即证4-2ab ≥2, 即ab ≤1,由①知成立.④欲证1a +1b ≥2,即证a +b ab≥2,即ab ≤1,由①知成立.4.已知a >0,b >0,则1a +1b+2ab 的最小值是_____________________________________.答案 4解析 因为1a +1b +2ab ≥21ab+2ab=2(1ab+ab )≥4.当且仅当1a =1b 且1ab=ab ,即a =b =1时,取“=”.5.(2014·山东改编)用反证法证明命题:“设a ,b 为实数,则方程x 3+ax +b =0至少有一个实根”时,要做的假设是________. 答案 方程x 3+ax +b =0没有实根解析 方程x 3+ax +b =0至少有一个实根的反面是方程x 3+ax +b =0没有实根. 6.下列条件:①ab >0;②ab <0;③a >0,b >0;④a <0,b <0. 其中能使b a +ab≥2成立的条件的个数是________. 答案 3解析 要使b a +a b ≥2,只要b a >0,且a b>0,即a 、b 不为0且同号,故有3个.7.已知“整数对”按如下规律排成一列:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第60个“整数对”是________. 答案 (5,7)解析 依题意,把“整数对”的和相同的分为一组,不难得知每组中每个“整数对”的和为n +1,且每组共有n 个“整数对”,这样的前n 组一共有n n +2个“整数对”,注意到+2<60<+2,因此第60个“整数对”处于第11组(每个“整数对”的和为12的组)的第5个位置,结合题意可知每个“整数对”的和为12的组中的各数对依次为(1,11),(2,10),(3,9),(4,8),(5,7),…,因此第60个“整数对”是(5,7).8.凸函数的性质定理:如果函数f (x )在区间D 上是凸函数,则对于区间D 内的任意x 1,x 2,…,x n ,有f x 1+f x 2+…+f x n n ≤f (x 1+x 2+…+x nn),已知函数y =sin x 在区间(0,π)上是凸函数,则在△ABC 中,sin A +sin B +sin C 的最大值为________. 答案332解析 ∵f (x )=sin x 在区间(0,π)上是凸函数,且A 、B 、C ∈(0,π). ∴f A +f B +f C3≤f (A +B +C3)=f (π3),即sin A +sin B +sin C ≤3sin π3=332,所以sin A +sin B +sin C 的最大值为332.9.已知非零向量a ⊥b ,求证:|a |+|b ||a -b |≤ 2.证明 ∵a ⊥b ,∴a ·b =0.要证|a |+|b ||a -b |≤2,只需证:|a |+|b |≤2|a -b |,平方得:|a |2+|b |2+2|a ||b |≤2(|a |2+|b |2-2a ·b ), 只需证:|a |2+|b |2-2|a ||b |≥0,即(|a |-|b |)2≥0,显然成立.故原不等式得证.10.已知四棱锥S -ABCD 中,底面是边长为1的正方形,又SB =SD =2,SA =1. (1)求证:SA ⊥平面ABCD ;(2)在棱SC 上是否存在异于S ,C 的点F ,使得BF ∥平面SAD ?若存在,确定F 点的位置;若不存在,请说明理由.(1)证明 由已知得SA 2+AD 2=SD 2,∴SA ⊥AD .同理SA ⊥AB .又AB ∩AD =A ,∴SA ⊥平面ABCD .(2)解 假设在棱SC 上存在异于S ,C 的点F ,使得BF ∥平面SAD . ∵BC ∥AD ,BC ⊄平面SAD .∴BC ∥平面SAD .而BC ∩BF =B ,∴平面FBC ∥平面SAD .这与平面SBC 和平面SAD 有公共点S 矛盾,∴假设不成立.故不存在这样的点F ,使得BF ∥平面SAD .B 组 专项能力提升(时间:30分钟)1.已知函数f (x )=(12)x ,a ,b 是正实数,A =f (a +b 2),B =f (ab ),C =f (2ab a +b),则A 、B 、C 的大小关系为____________.答案 A ≤B ≤C解析 ∵a +b 2≥ab ≥2ab a +b ,又f (x )=(12)x 在R 上是减函数. ∴f (a +b 2)≤f (ab )≤f (2ab a +b ),即A ≤B ≤C . 2.(2013·广东)设整数n ≥4,集合X ={1,2,3,…,n },令集合S ={(x ,y ,z )|x ,y ,z ∈X ,且三条件x <y <z ,y <z <x ,z <x <y 恰有一个成立}.若(x ,y ,z )和(z ,w ,x )都在S 中,则下列选项正确的是________.①(y ,z ,w )∈S ,(x ,y ,w )∉S②(y ,z ,w )∈S ,(x ,y ,w )∈S③(y ,z ,w )∉S ,(x ,y ,w )∈S④(y ,z ,w )∉S ,(x ,y ,w )∉S答案 ②解析 因为(x ,y ,z )∈S ,则x ,y ,z 的大小关系有3种情况,同理,(z ,w ,x )∈S ,则z ,w ,x 的大小关系也有3种情况,如图所示,由图可知,x ,y ,w ,z 的大小关系有4种可能,均符合(y ,z ,w )∈S ,(x ,y ,w )∈S .故②正确.3.a 2+2+2a 2+2与22的大小关系是________________. 答案 a 2+2+2a 2+2>2 2 4.已知二次函数f (x )=ax 2+bx +c (a >0)的图象与x 轴有两个不同的交点,若f (c )=0,且0<x <c 时,f (x )>0.(1)证明:1a是函数f (x )的一个零点; (2)试用反证法证明1a>c . 证明 (1)∵f (x )图象与x 轴有两个不同的交点, ∴f (x )=0有两个不等实根x 1,x 2,∵f (c )=0,∴x 1=c 是f (x )=0的根,又x 1x 2=c a ,∴x 2=1a (1a≠c ), ∴1a是f (x )=0的一个根. 即1a 是函数f (x )的一个零点.(2)假设1a <c ,又1a>0,由0<x <c 时,f (x )>0, 知f (1a )>0与f (1a )=0矛盾,∴1a≥c , 又∵1a ≠c ,∴1a>c . 5.已知数列{a n }满足:a 1=12,+a n +11-a n =+a n 1-a n +1,a n a n +1<0(n ≥1),数列{b n }满足:b n =a 2n +1-a 2n (n ≥1). (1)求数列{a n },{b n }的通项公式;(2)证明:数列{b n }中的任意三项不可能成等差数列.(1)解 由题意可知,1-a 2n +1=23(1-a 2n ). 令c n =1-a 2n ,则c n +1=23c n . 又c 1=1-a 21=34,则数列{c n }是首项为c 1=34, 公比为23的等比数列,即c n =34·(23)n -1, 故1-a 2n =34·(23)n -1⇒a 2n =1-34·(23)n -1. 又a 1=12>0.a n a n +1<0,故a n =(-1)n -1 1-3423n -1.b n =a 2n +1-a 2n=[1-34·(23)n ]-[1-34·(23)n -1] =14·(23)n -1. (2)证明 用反证法证明.假设数列{b n }存在三项b r ,b s ,b t (r <s <t )按某种顺序成等差数列,由于数列{b n }是首项为14,公比为23的等比数列, 于是有b r >b s >b t ,则只能有2b s =b r +b t 成立.∴2·14(23)s -1=14(23)r -1+14(23)t -1, 两边同乘以3t -121-r ,化简得3t -r +2t -r =2·2s -r 3t -s . 由于r <s <t ,∴上式左边为奇数,右边为偶数, 故上式不可能成立,导致矛盾.故数列{b n }中任意三项不可能成等差数列.。

学案36 直接证明与间接证明导学目标: 1.了解直接证明的两种基本方法——分析法和综合法;了解分析法和综合法的思考过程及特点.2.了解间接证明的一种基本方法——反证法,了解反证法的思考过程及特点.自主梳理 1.直接证明 (1)综合法①定义:从已知条件出发,以______________________为依据,逐步下推,直到推出所要证明的结论为止,这种证明方法叫做综合法.②框图表示:P ⇒Q 1→Q 1⇒Q 2→Q 2⇒Q 3→…→Q n ⇒Q (其中P 表示已知条件,Q 表示要证的结论).(2)分析法①定义:从问题的结论出发,追溯导致结论成立的条件,逐步上溯,直到使________________和______________________为止.这种证明方法叫做分析法.②框图表示:Q ⇐P 1→P 1⇐P 2→P 2⇐P 3→…→得到一个明显成立的条件.2.间接证明反证法:假设原命题________(即在原命题的条件下,结论不成立),经过正确的推理,最后得出________,因此说明假设错误,从而证明了原命题成立,这样的证明方法叫做反证法.自我检测 1.分析法是从要证的结论出发,寻求使它成立的________条件.(填“充分”、“必要”或“充要”)2.(2010·揭阳高三统考)用反证法证明“如果a >b ,那么3a >3b ”的假设内容应是__________________.3.设a 、b 、c 是互不相等的正数,则下列不等式中不恒成立的是________.(填序号). ①|a -c |≤|a -b |+|c -b |;②a 2+1a2≥a +1a;③a +3-a +1<a +2-a ;④|a -b |+1a -b≥2. 4.已知a +b >0,则a b2+b a2与1a +1b的大小关系为____________________.5.(2010·东北三省四市联考)设x 、y 、z ∈R +,a =x +1y ,b =y +1z ,c =z +1x,证明a ,b ,c 中至少有一个不小于2.探究点一 综合法例1 已知a ,b ,c 都是实数,求证:a 2+b 2+c 2≥13(a +b +c )2≥ab +bc +ca .变式迁移1 设a ,b ,c >0,证明:a 2b +b 2c +c 2a≥a +b +c .探究点二 分析法例2 若a ,b ,c 是不全相等的正数,求证: lg a +b 2+lg b +c 2+lg c +a 2>lg a +lg b +lg c .变式迁移2 已知a >0,求证: a 2+1a 2-2≥a +1a-2.探究点三 反证法例3 若x ,y 都是正实数,且x +y >2,求证:1+x y <2与1+y x<2中至少有一个成立.式迁移3 若a ,b ,c 均为实数,且a =x 2-2y +π2,b =y 2-2z +π3,c =z 2-2x +π6.求证:a ,b ,c 中至少有一个大于0.转化与化归思想例 (14分)(2010·上海改编)若实数x 、y 、m 满足|x -m |>|y -m |,则称x 比y 远离m .(1)若x 2-1比1远离0,求x 的取值范围.(2)对任意两个不相等的正数a 、b ,证明:a 3+b 3比a 2b +ab 2远离2ab ab . 多角度审题 (1)本题属新定义题,根据“远离”的含义列出不等式,然后加以求解.(2)第(2)小题,实质是证明不等式|a 3+b 3-2ab ab |>|a 2b +ab 2-2ab ab |成立.证明时注意提取公因式及配方法的运用.【答题模板】(1)解 由题意得||x 2-1>1,即x 2-1>1或x 2-1<-1.[2分]由x 2-1>1,得x 2>2,即x <-2或x >2;由x 2-1<-1,得x ∈∅.综上可知x 的取值范围为(-∞,-2)∪(2,+∞).[4分](2)证明 由题意知即证||a 3+b 3-2ab ab >||a 2b +ab 2-2ab ab 成立.[8分] ∵a ≠b ,且a 、b 都为正数,∴||a 3+b 3-2ab ab =|| a 3 2+ b 3 2-2a 3b 3=|| a 3-b 3 2=(a a -b b )2,||a 2b +ab 2-2abab =||ab a +b -2ab =ab (a -b )2=(a b -b a )2,[10分]即证(a a -b b )2-(a b -b a )2>0,即证(a a -b b -a b +b a )(a a -b b +a b -b a )>0,需证[] a -b a +b [] a -b a +b >0,[12分]即证(a +b )(a -b )2>0,∵a 、b 都为正数且a ≠b , ∴上式成立.故原命题成立.[14分] 【突破思维障碍】1.准确理解题意,提炼出相应不等式是解决问题的关键.2.代数式|a 3+b 3-2ab ab |与|a 2b +ab 2-2ab ab |中的绝对值符号去掉为后续等价变形提供了方便.【易错点剖析】1.推理论证能力较差,绝对值符号不会去.2.运用能力较差,不能有效地进行式子的等价变形或中间变形出错.1.综合法是从条件推导到结论的思维方法,它是从已知条件出发,经过逐步的推理,最后达到待证的结论.即由因导果.2.分析法是从待证结论出发,一步一步地寻求结论成立的充分条件,最后达到题设的已知条件或已被证明的事实.即执果索因,用分析法寻找解题思路,再用综合法书写,这样比较有条理,叫分析综合法.3.用反证法证明问题的一般步骤:(1)反设:假设命题的结论不成立,即假定原结论的反面为真;(否定结论)(2)归谬:从反设和已知条件出发,经过一系列正确的逻辑推理,得出矛盾结果;(推导矛盾)(3)存真:由矛盾结果断定反设不真,从而肯定原结论成立.(结论成立)(满分:90分)一、填空题(每小题6分,共48分)1.用反证法证明命题“若整系数一元二次方程ax 2+bx +c =0 (a ≠0)有有理数根,那么a 、b 、c 中至少有一个是偶数”.假设内容应为____________________________________.2.(2010·无锡模拟)设a ,b 是两个实数,给出下列条件: (1)a +b >1;(2)a +b =2;(3)a +b >2;(4)a 2+b 2>2;(5)ab >1.其中能推出:“a ,b 中至少有一个大于1”的条件是______.(填序号)3.设a 、b 、c ∈(0,+∞),P =a +b -c ,Q =b +c -a ,R =c +a -b ,则“PQR >0”是“P 、Q 、R 同时大于零”的________条件.4.(2010·安徽)若a >0,b >0,a +b =2,则下列不等式对一切满足条件的a ,b 恒成立的是________(写出所有正确命题的序号).①ab ≤1;②a +b ≤2;③a 2+b 2≥2;④a 3+b 3≥3; ⑤1a +1b≥2.5.如果△A 1B 1C 1的三个内角的余弦值分别等于△A 2B 2C 2的三个内角的正弦值,则△A 2B 2C 2是________三角形(填“锐角”“钝角”或“直角”).6.(2010·江苏前黄高级中学模拟)某同学准备用反证法证明如下一个问题:函数f (x )在[0,1]上有意义,且f (0)=f (1),如果对于不同的x 1,x 2∈[0,1],都有|f (x 1)-f (x 2)|<|x 1-x 2|,求证:|f (x 1)-f (x 2)|<12.那么他的反设应该是__________________________________________________________________________________________________________________________. 7.对于任意实数a ,b 定义运算a *b =(a +1)(b +1)-1,给出以下结论: ①对于任意实数a ,b ,c ,有a *(b +c )=(a *b )+(a *c ); ②对于任意实数a ,b ,c ,有a *(b *c )=(a *b )*c ; ③对于任意实数a ,有a *0=a .则以上结论正确的是________.(写出你认为正确的结论的所有序号)8.(2011·天津)已知log 2a +log 2b ≥1,则3a +9b的最小值为________.二、解答题(共42分)9.(14分)已知非零向量a 、b ,a ⊥b ,求证:|a |+|b ||a -b |≤ 2.10.(14分)已知a 、b 、c >0,求证:a 3+b 3+c 3≥13(a 2+b 2+c 2)(a +b +c ).11.(14分)已知a 、b 、c ∈(0,1),求证:(1-a )b ,(1-b )c ,(1-c )a 不能同时大于14.学案36 直接证明与间接证明答案自主梳理1.(1)①已知的定义、公理、定理 (2)①结论成立的条件 已知条件或已知事实吻合 2.不成立 矛盾自我检测 1.充分解析 由分析法的定义可知.2.3a ≤3b解析 3a >3b 的否定是3a ≤3b . 3.④解析 ④选项成立时需得证a -b >0.①中|a -b |+|c -b |≥|(a -b )-(c -b )|=|a -c |,②作差可证;③移项平方可证. 4.a b2+b a 2≥1a +1b解析 a b 2+b a 2-⎝ ⎛⎭⎪⎫1a +1b =a -b b 2+b -a a2=(a -b )⎝ ⎛⎭⎪⎫1b 2-1a 2= a +b a -b 2a 2b 2.∵a +b >0,(a -b )2≥0,∴ a +b a -b 2a 2b 2≥0.∴a b 2+b a 2≥1a +1b. 5.证明 假设a ,b ,c 均小于2,则a +b +c <6.①又a +b +c =x +1y +y +1z +z +1x=(x +1x )+(y +1y )+(z +1z)≥6,这与①式相矛盾,∴假设不正确. ∴a ,b ,c 至少有一个不小于2. 课堂活动区例1 解题导引 综合法证明不等式,要特别注意基本不等式的运用和对题设条件的运用.这里可从基本不等式相加的角度先证得a 2+b 2+c 2≥ab +bc +ca 成立,再进一步得出结论.证明 ∵a 2+b 2≥2ab ,b 2+c 2≥2bc ,c 2+a 2≥2ca ,三式相加得a 2+b 2+c 2≥ab +bc +ca ,∴3a 2+3b 2+3c 2≥(a 2+b 2+c 2)+2(ab +bc +ca )=(a +b +c )2.∴a 2+b 2+c 2≥13(a +b +c )2;∵a 2+b 2+c 2≥ab +bc +ca , ∴a 2+b 2+c 2+2(ab +bc +ca )≥ab +bc +ca +2(ab +bc +ca ),∴(a +b +c )2≥3(ab +bc +ca ). ∴原命题得证.变式迁移1 证明 ∵a ,b ,c >0,根据基本不等式,有a 2b +b ≥2a ,b 2c +c ≥2b ,c 2a+a ≥2c . 三式相加:a 2b +b 2c +c2a+a +b +c ≥2(a +b +c ).即a 2b +b 2c +c2a≥a +b +c . 例2 解题导引 当所给的条件简单,而所证的结论复杂,一般采用分析法.含有根号、对数符号、绝对值的不等式,若从题设不易推导时,可以考虑分析法.证明 要证lg a +b 2+lg b +c 2+lg c +a2>lg a +lg b +lg c ,只需证lg ⎝ ⎛⎭⎪⎫a +b 2·b +c 2·c +a 2>lg(a ·b ·c ),只需证a +b 2·b +c 2·c +a 2>abc .(中间结果)因为a ,b ,c 是不全相等的正数, 则a +b 2≥ab >0,b +c 2≥bc >0,c +a 2≥ca >0.且上述三式中的等号不全成立,所以a +b 2·b +c 2·c +a 2>abc .(中间结果)所以lg a +b 2+lg b +c 2+lg c +a2>lg a +lg b +lg c .变式迁移2 证明 要证 a 2+1a 2-2≥a +1a-2,只要证a 2+1a 2+2≥a +1a+ 2.∵a >0,故只要证 ⎝⎛⎭⎪⎫a 2+1a 2+22≥⎝⎛⎭⎪⎫a +1a +22,即a 2+1a2+4a 2+1a2+4≥a 2+2+1a2+22⎝ ⎛⎭⎪⎫a +1a +2,从而只要证2a 2+1a 2≥2⎝ ⎛⎭⎪⎫a +1a ,只要证4⎝ ⎛⎭⎪⎫a 2+1a 2≥2⎝ ⎛⎭⎪⎫a 2+2+1a 2,即a 2+1a2≥2,而该不等式显然成立,故原不等式成立.例3 解题导引 (1)当一个命题的结论是以“至多”、“至少”、“惟一”或以否定形式出现时,宜用反证法来证,反证法的关键是在正确的推理下得出矛盾,矛盾可以是①与已知条件矛盾,②与假设矛盾,③与定义、公理、定理矛盾,④与事实矛盾等方面,反证法常常是解决某些“疑难”问题的有力工具,是数学证明中的一件有力武器.(2)利用反证法证明问题时,要注意与之矛盾的定理不能是用本题的结论证明的定理,否则,将出现循环论证的错误.证明 假设1+x y <2和1+yx<2都不成立,则有1+x y ≥2和1+y x ≥2同时成立,因为x >0且y >0,所以1+x ≥2y ,且1+y ≥2x , 两式相加,得2+x +y ≥2x +2y ,所以x +y ≤2,这与已知条件x +y >2相矛盾,因此1+x y <2与1+y x<2中至少有一个成立.变式迁移3 证明 假设a ,b ,c 都不大于0,即a ≤0,b ≤0,c ≤0.∵a =x 2-2y +π2,b =y 2-2z +π3,c =z 2-2x +π6,∴x 2-2y +π2+y 2-2z +π3+z 2-2x +π6=(x -1)2+(y -1)2+(z -1)2+(π-3)≤0, ①又∵(x -1)2+(y -1)2+(z -1)2≥0,π-3>0,∴(x -1)2+(y -1)2+(z -1)2+(π-3)>0. ② ①式与②式矛盾, ∴假设不成立,即a ,b ,c 中至少有一个大于0. 课后练习区1.假设a 、b 、c 都不是偶数 2.(3)解析 若a =12,b =23,则a +b >1,但a <1,b <1,故(1)推不出;若a =b =1,则a +b =2,故(2)推不出;若a =-2,b =-3,则a 2+b 2>2,故(4)推不出; 若a =-2,b =-3,则ab >1,故(5)推不出;对于(3),即a +b >2,则a ,b 中至少有一个大于1, 反证法:假设a ≤1且b ≤1, 则a +b ≤2与a +b >2矛盾,因此假设不成立,故a ,b 中至少有一个大于1.3.充要解析 必要性是显然成立的,当PQR >0时,若P 、Q 、R 不同时大于零,则其中两个为负,一个为正,不妨设P >0,Q <0,R <0,则Q +R =2c <0,这与c >0矛盾,即充分性也成立.4.①③⑤解析 ①ab ≤(a +b 2)2=1,成立.②欲证a +b ≤2,即证a +b +2ab ≤2,即2ab ≤0,显然不成立.③欲证a 2+b 2=(a +b )2-2ab ≥2, 即证4-2ab ≥2,即ab ≤1,由①知成立. ④a 3+b 3=(a +b )(a 2-ab +b 2)≥3⇔a 2-ab +b 2≥32⇔(a +b )2-3ab ≥32⇔4-32≥3ab ⇔ab ≤56,由①知,ab ≤56不恒成立.⑤欲证1a +1b ≥2,即证a +b ab≥2,即ab ≤1,由①知成立.5.钝角解析 由条件知,△A 1B 1C 1的三个内角的余弦值均大于0,则△A 1B 1C 1是锐角三角形,假设△A 2B 2C 2是锐角三角形,由⎩⎪⎨⎪⎧ sin A 2=cos A 1=sin ⎝ ⎛⎭⎪⎫π2-A 1,sin B 2=cos B 1=sin ⎝ ⎛⎭⎪⎫π2-B 1,sin C 2=cos C 1=sin ⎝ ⎛⎭⎪⎫π2-C 1得⎩⎪⎨⎪⎧A 2=π2-A 1,B 2=π2-B 1,C 2=π2-C 1,那么,A 2+B 2+C 2=π2,这与三角形内角和为π相矛盾,所以假设不成立,所以△A 2B 2C 2是钝角三角形.6.“∃x 1,x 2∈[0,1],使得|f (x 1)-f (x 2)|<|x 1-x 2|,则|f (x 1)-f (x 2)|≥12”7.②③解析 按新定义,可以验证a *(b +c )≠(a *b )+(a *c ); 所以①不成立;而a *(b *c )=(a *b )*c 成立,a *0=(a +1)(0+1)-1=a .所以正确的结论是②③. 8.18解析 由log 2a +log 2b ≥1得log 2(ab )≥1,即ab ≥2,∴3a +9b =3a +32b ≥2×3a +2b 2(当且仅当3a =32b,即a =2b 时“=”号成立).又∵a +2b ≥22ab ≥4(当且仅当a =2b 时“=”成立), ∴3a +9b ≥2×32=18.即当a =2b 时,3a +9b有最小值18.9.证明 ∵a ⊥b ,∴a·b =0. (2分)要证|a |+|b ||a -b |≤2,只需证:|a |+|b |≤2|a -b |, (6分)平方得:|a |2+|b |2+2|a||b |≤2(|a |2+|b |2-2a·b ), (10分)只需证:|a |2+|b |2-2|a||b |≥0, (12分)即(|a |-|b |)2≥0,显然成立.故原不等式得证. (14分)10.证明 ∵a 2+b 2≥2ab ,a 、b 、c >0,∴(a 2+b 2)(a +b )≥2ab (a +b ), (3分) ∴a 3+b 3+a 2b +ab 2≥2ab (a +b )=2a 2b +2ab 2, ∴a 3+b 3≥a 2b +ab 2.(7分)同理,b 3+c 3≥b 2c +bc 2,a 3+c 3≥a 2c +ac 2, 将三式相加得, 2(a 3+b 3+c 3)≥a 2b +ab 2+b 2c +bc 2+a 2c +ac 2.(10分)∴3(a 3+b 3+c 3)≥(a 3+a 2b +a 2c )+(b 3+b 2a +b 2c )+(c 3+c 2a +c 2b )=(a +b +c )(a 2+b 2+c 2).∴a 3+b 3+c 3≥13(a 2+b 2+c 2)(a +b +c ).(14分)11.证明 方法一 假设三式同时大于14,即(1-a )b >14,(1-b )c >14,(1-c )a >14,(3分)∵a 、b 、c ∈(0,1),∴三式同向相乘得(1-a )b (1-b )c (1-c )a >164.(8分)又(1-a )a ≤⎝ ⎛⎭⎪⎫1-a +a 22=14,(10分)同理(1-b )b ≤14,(1-c )c ≤14,∴(1-a )a (1-b )b (1-c )c ≤164,(12分)这与假设矛盾,故原命题正确.(14分)方法二 假设三式同时大于14,∵0<a <1,∴1-a >0,(2分) 1-a +b 2≥ 1-a b > 14=12,(8分) 同理 1-b +c 2>12, 1-c +a 2>12,(10分)三式相加得32>32,这是矛盾的,故假设错误,∴原命题正确.(14分)。

高一数学直接证明与间接证明试题答案及解析1.用反证法证明命题“若a2+b2=0,则a、b全为0(a、b∈R)”,其反设正确的是()A.a、b至少有一个不为0B.a、b至少有一个为0C.a、b全不为0D.a、b中只有一个为0【答案】A【解析】把要证的结论否定之后,即得所求的反设.解:由于“a、b全为0(a、b∈R)”的否定为:“a、b至少有一个不为0”,故选 A.点评:本题考查用反证法证明数学命题,得到“a、b全为0(a、b∈R)”的否定为:“a、b至少有一个不为0”,是解题的关键.2.“用反证法证明命题“如果x<y,那么x<y”时,假设的内容应该是()A.x=yB.x<yC.x=y且x<yD.x=y或x>y【答案】D【解析】由于用反证法证明命题时,应先假设命题的否定成立,而“x<y”的否定为:“x≥y ”.解:∵用反证法证明命题时,应先假设命题的否定成立,而“x<y”的否定为:“x=y或x >y”,故选D.点评:本题主要考查用命题的否定,反证法证明数学命题的方法和步骤,把要证的结论进行否定,得到要证的结论的反面,是解题的突破口,属于中档题.3.已知a、b、c是△ABC的三边长,A=,B=,则()A.A>B B.A<B C.A≥B D.A≤B【答案】A【解析】由题意得 c<a+b,故 B==<,变形后再放大,可证小于 A.解:∵a、b、c是△ABC的三边长,∴c<a+b,∴B==<==+<+=A,∴B<A,故选 A.点评:本题考查三角形的边长的性质,用放缩法证明不等式.4.用反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:①A+B+C=90°+90°+C>180°,这与三角形内角和为180°相矛盾,A=B=90°不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角A、B、C中有两个直角,不妨设A=B=90°,正确顺序的序号为()A.①②③B.①③②C.②③①D.③①②【答案】D【解析】根据反证法的证法步骤知:第一步反设,假设三角形的三个内角A、B、C中有两个直角,不妨设A=B=90°,正确.第二步得出矛盾:A+B+C=90°+90°+C>180°,这与三角形内角和为180°相矛盾,A=B=90°不成立;第三步下结论:所以一个三角形中不能有两个直角.从而得出正确选项.解:根据反证法的证法步骤知:假设三角形的三个内角A、B、C中有两个直角,不妨设A=B=90°,正确A+B+C=90°+90°+C>180°,这与三角形内角和为180°相矛盾,A=B=90°不成立;所以一个三角形中不能有两个直角.故顺序的序号为③①②.故选D.点评:反证法是一种简明实用的数学证题方法,也是一种重要的数学思想.相对于直接证明来讲,反证法是一种间接证法.它是数学学习中一种很重要的证题方法.其实质是运用“正难则反”的策略,从否定结论出发,通过逻辑推理,导出矛盾.5.用反证法证明:“a>b”,应假设为()A.a>b B.a<b C.a=b D.a≤b【答案】D【解析】用反证明法证明,要先假设原命题不成立,即先要否定原命题.解:用反证明法证明,要先假设原命题不成立,即先要否定原命题,故用反证法证明:“a>b”,应假设为“a≤b”,故选D.点评:本题考查反证法的解题过程和证明方法,解题时要认真审题,仔细解答.6.关于综合法和分析法说法错误的是()A.综合法和分析法是直接证明中最基本的两种证明方法B.综合法又叫顺推证法或由因导果法C.分析法又叫逆推证法或执果索因法D.综合法和分析法都是因果分别互推的两头凑法【答案】D【解析】根据综合法、分析法的定义可得结论.解:根据综合法的定义可得,综合法是执因导果法,是顺推法;根据分析法的定义可得,分析法是执果索因法,是直接证法.故选:D.点评:本题主要考查综合法、分析法的定义,属于基础题.7.某同学证明+<+的过程如下:∵﹣>﹣>0,∴<,∴<,∴+<+,则该学生采用的证明方法是()A.综合法B.比较法C.反证法D.分析法【答案】A【解析】从推理过程(是“执因索果”还是“执果索因”)即可得到答案.解:从推理形式来看,从﹣>﹣>0入手,推出<,继而得到<,最后得到+<+,是“执因索果”,是综合法证明,故选:A.点评:本题考查综合法与分析法,掌握二者的推理形式(“执因索果”为综合法,“执果索因”为分析法)是关键,属于中档题.8.要证:a2+b2﹣1﹣a2b2≤0,只要证明()A.2ab﹣1﹣a2b2≤0B.a2+b2﹣1﹣≤0C.﹣1﹣a2b2≤0D.(a2﹣1)(b2﹣1)≥0【答案】D【解析】将左边因式分解,即可得出结论.解:要证:a2+b2﹣1﹣a2b2≤0,只要证明(a2﹣1)(1﹣b2)≤0,只要证明(a2﹣1)(b2﹣1)≥0.故选:D.点评:综合法(由因导果)证明不等式、分析法(执果索因)证明不等式.9.下面叙述正确的是()A.综合法、分析法是直接证明的方法B.综合法是直接证法、分析法是间接证法C.综合法、分析法所用语气都是肯定的D.综合法、分析法所用语气都是假定的【答案】A【解析】根据综合法、分析法的定义与证题思路,可得结论.解:综合法(由因导果)证明不等式、分析法(执果索因)证明不等式,是直接证明的方法.故选:A.点评:综合法(由因导果)证明不等式、分析法(执果索因)证明不等式.10.求证:+>.证明:因为+和都是正数,所以为了证明+>,只需证明(+)2>()2,展开得5+2>5,即2>0,显然成立,所以不等式+>.上述证明过程应用了()A.综合法B.分析法C.综合法、分析法混合D.间接证法【答案】B【解析】分析法是果索因,基本步骤:要证…只需证…,只需证…,分析法是从求证的不等式出发,找到使不等式成立的充分条件,把证明不等式的问题转化为判定这些充分条件是否具有的问题.解:分析法是果索因,基本步骤:要证…只需证…,只需证…结合证明过程,证明过程应用了分析法.故选:B.点评:解决本题的关键是对分析法的概念要熟悉,搞清分析法证题的理论依据,掌握分析法的证11.下列对分析法表述正确的是;(填上你认为正确的全部序号)①由因导果的推法;②执果索因的推法;③因果分别互推的两头凑法;④逆命题的证明方法.【答案】②【解析】根据分析法的定义可得,分析法是执果索因法.解:根据分析法的定义可得,分析法是执果索因法,是直接证法.故答案为:②.点评:本题主要考查综合法、分析法、反证法的定义,属于基础题.12.命题“对于任意角θ,cos4θ﹣sin4θ=cos2θ”的证明:“cos4θ﹣sin4θ=(cos2θ﹣sin2θ)(cos2θ+sin2θ)=cos2θ﹣sin2θ=cos2θ”过程应用了()A.分析发B.综合法C.综合法、分析法结合使用D.间接证法【答案】B【解析】在推理的过程中使用了因式分解,平方差公式,以及余弦的倍角公式,符合综合法的证明过程.解:在证明过程中使用了大量的公式和结论,有平方差公式,同角的关系式,所以在证明过程中,使用了综合法的证明方法.故选:B.点评:本题主要考查证明方法的选择和判断,比较基础.13.证明不等式的最适合的方法是()A.综合法B.分析法C.间接证法D.合情推理法【答案】B【解析】要证原不等式成立,只要证<,即证9+2<9+2,故只要证<,即证14<18,此种证明方法是分析法.解:要证明不等式,只要证<,即证9+2<9+2,故只要证<,即证14<18.以上证明不等式所用的最适合的方法是分析法.故选B.点评:本题考查的是分析法和综合法,解答此题的关键是熟知比较大小的方法.从求证的不等式出发,“由果索因”,逆向逐步找这个不等式成立需要具备的充分条件,分析法──通过对事物原因或结果的周密分析,从而证明论点的正确性、合理性的论证方法.也称为因果分析,属于中档题.14.设()A.都大于2B.至少有一个大于2C.至少有一个不小于2D.至少有一个不大于2【解析】假设:中都小于2,则,但由于=≥2+2+2=6,出现矛盾,从而得出正确答案:中至少有一个不小于2.解:由于=≥2+2+2=6,∴中至少有一个不小于2,故选C.点评:分析法──通过对事物原因或结果的周密分析,从而证明论点的正确性、合理性的论证方法,也称为因果分析,从求证的不等式出发,“由果索因”,逆向逐步找这个不等式成立需要具备的充分条件;综合法是指从已知条件出发,借助其性质和有关定理,经过逐步的逻辑推理,最后达到待证结论或需求问题,其特点和思路是“由因导果”,即从“已知”看“可知”,逐步推向“未知”.15.已知函数f(x)=|sinx|的图象与直线y=kx(k>0)有且仅有三个交点,交点的横坐标的最大值为α,.则()A.A>B B.A<BC.A=B D.A与B的大小不确定【答案】C【解析】作出函数f(x)=|sinx|的图象,利用函数f(x)=|sinx|的图象与直线y=kx(k>0)有且仅有三个交点,确定切点坐标,然后利用三角函数的关系即可得到结论.解:作出函数f(x)=|sinx|的图象与直线y=kx(k>0)的图象,如图所示,要使两个函数有且仅有三个交点,则由图象可知,直线在()内与f(x)相切.设切点为A(α,﹣sinα),当x∈()时,f(x)=|sinx|=﹣sinx,此时f'(x)=﹣cosx,x∈().∴﹣cos,即α=tanα,∴==.即A=B.故选:C.点评:本题主要考查三角函数的图象和性质,利用数形结合是解决本题的关键.16.设函数f(x)=,类比课本推导等差数列的前n项和公式的推导方法计算f(﹣5)+f(﹣4)+f(﹣3))+…+f(0))+f(1))+…+f(5)+f(6)的值为()A.B.C.3D.【答案】C【解析】根据课本中推导等差数列前n项和的公式的方法﹣倒序相加法,观察所求式子的特点,应先求f(x)+f(1﹣x)的值.解:∵f(x)=∴f(x)+f(1﹣x)=+=+==,即f(﹣5)+f(6)=,f(﹣4)+f(5)=,f(﹣3)+f(4)=,f(﹣2)+f(3)=,f(﹣1)+f(2)=,f(0)+f(1)=,∴所求的式子值为3 .故选C.点评:本题为规律性的题目,要善于观察式子的特点,并且此题给出了明确的方法,从而降低了本题难度.17.(2014•北京)学生的语文、数学成绩均被评定为三个等级,依次为“优秀”“合格”“不合格”.若学生甲的语文、数学成绩都不低于学生乙,且其中至少有一门成绩高于乙,则称“学生甲比学生乙成绩好”.如果一组学生中没有哪位学生比另一位学生成绩好,并且不存在语文成绩相同、数学成绩也相同的两位学生,则这一组学生最多有()A.2人B.3人C.4人D.5人【答案】B【解析】分别用ABC分别表示优秀、及格和不及格,根据题干中的内容推出文成绩得A,B,C 的学生各最多只有1个,继而推得学生的人数.解:用ABC分别表示优秀、及格和不及格,显然语文成绩得A的学生最多只有1个,语文成绩得B得也最多只有一个,得C最多只有一个,因此学生最多只有3人,显然(AC)(BB)(CA)满足条件,故学生最多有3个.故选:B.点评:本题主要考查了合情推理,关键是找到语句中的关键词,培养了推理论证的能力.18.(2014•揭阳三模)对于正实数α,Mα为满足下述条件的函数f(x)构成的集合:∀x1,x2∈R且x2>x1,有﹣α(x2﹣x1)<f(x2)﹣f(x1)<α(x2﹣x1).下列结论中正确的是()A.若f(x)∈Mα1,g(x)Mα2,则f(x)•g(x)∈Mα1•α2B.若f(x)∈Mα1,g(x)∈Mα2,且g(x)≠0,则C.若f(x)∈Mα1,g(x)∈Mα2,则f(x)+g(x)∈Mα1+α2D.若f(x)∈Mα1,g(x)∈Mα2,且α1>α2,则f(x)﹣g(x)∈Mα1﹣α2【答案】C【解析】对于﹣α(x2﹣x1)<f(x2)﹣f(x1)<α(x2﹣x1).变形有,令,不妨设f(x)∈Mα1,g(x))∈Mα2,利用不等式的性质可得f(x)+g(x)∈Mα1+α2.从而得出正确答案.解:对于﹣α(x2﹣x1)<f(x2)﹣f(x1)<α(x2﹣x1),即有,令,有﹣α<k<α,不妨设f(x)∈Mα1,g(x))∈Mα2,即有﹣α1<kf<α1,﹣α2<kg<α2,因此有﹣α1﹣α2<kf+kg<α1+α2,因此有f(x)+g(x)∈Mα1+α2.故选C.点评:本题考查的是元素与集合关系的判断、进行简单的合情推理、函数恒成立问题,在能力上主要考查对新信息的理解力及解决问题的能力.19.(2014•枣庄一模)在实数集R中定义一种运算“*”,对任意a,b∈R,a*b为唯一确定的实数,且具有性质:(1)对任意a∈R,a*0=a;(2)对任意a,b∈R,a*b=ab+(a*0)+(b*0).则函数f(x)=(e x)*的最小值为()A.2B.3C.6D.8【答案】B【解析】根据性质,f(x)=(e x)*=1+e x+,利用基本不等式,即可得出结论.解:根据性质,f(x)=(e x)*=1+e x+≥1+2=3,当且仅当e x=时,f(x)=(e x)*的最小值为3.故选:B.点评:本题考查新定义,考查基本不等式的运用,正确理解新定义是关键.20.(2014•泸州一模)一支人数是5的倍数且不少于1000人的游行队伍,若按每横排4人编队,最后差3人;若按每横排3人编队,最后差2人;若按每横排2人编队,最后差1人.则这只游行队伍的最少人数是()A.1025B.1035C.1045D.1055【答案】C【解析】由已知可设这只游行队伍的最少人数是n,则n﹣1是2,3,4的公倍数,即12的倍数,且n为5和倍数,进而可得答案.解:设这只游行队伍的最少人数是n∵每横排4人编队,最后差3人;若按每横排3人编队,最后差2人;若按每横排2人编队,最后差1人.∴n﹣1是2,3,4的公倍数,即12的倍数即n﹣1=1008+12k,k∈N则n=1009+12k,k∈N又∵n为5的倍数故当k=3时,1045是满足条件的最少人数故选C点评:本题是典型的“韩信点兵”问题,解答的关键是将问题转化为公倍数问题.。

课时作业42 直接证明与间接证明一、选择题1.命题“对于任意角θ,cos 4θ-sin 4θ=cos2θ”的证明:“cos 4θ-sin 4θ=(cos 2θ-sin 2θ)(cos 2θ+sin 2θ)=cos 2θ-sin 2θ=cos2θ”过程应用了( )A .分析法B .综合法C .综合法、分析法综合使用D .间接证明法解析:因为证明过程是“从左往右”,即由条件⇒结论. 答案:B2.若a ,b ∈R ,则下面四个式子中恒成立的是( ) A .lg(1+a 2)>0 B .a 2+b 2≥2(a -b -1) C .a 2+3ab >2b 2D.a b <a +1b +1解析:在B 项中,∵a 2+b 2-2(a -b -1)=(a 2-2a +1)+(b 2+2b +1)=(a -1)2+(b +1)2≥0,∴a 2+b 2≥2(a -b -1)恒成立.答案:B3.在△ABC 中,sin A sin C <cos A cos C ,则△ABC 一定是( ) A .锐角三角形 B .直角三角形 C .钝角三角形D .不确定解析:由sin A sin C <cos A cos C 得, cos A cos C -sin A sin C >0, 即cos(A +C )>0,∴A +C 是锐角, 从而B >π2,故△ABC 必是钝角三角形.答案:C4.设a ,b ,c 是不全相等的正数,给出下列判断: ①(a -b )2+(b -c )2+(c -a )2≠0; ②a >b ,a <b 及a =b 中至少有一个成立; ③a ≠c ,b ≠c ,a ≠b 不能同时成立. 其中正确判断的个数为( )A .0B .1C .2D .3解析:①②正确;③中,a ≠b ,b ≠c ,a ≠c 可以同时成立,如a =1,b =2,c =3,故正确的判断有2个.答案:C5.若P =a +a +7,Q =a +3+a +4(a ≥0),则P ,Q 的大小关系为( ) A .P >Q B .P =Q C .P <QD .由a 取值决定解析:假设P <Q ,要证P <Q ,只要证P 2<Q 2, 只要证2a +7+2aa +7<2a +7+2a +3a +4,只要证a 2+7a <a 2+7a +12,只要证0<12, ∵0<12成立,∴P <Q 成立. 答案:C6.设函数f (x )是定义在R 上的以3为周期的奇函数,若f (1)>1,f (2)=3a -4a +1,则a的取值范围是( )A .a <34B .a <34且a ≠-1C .a >34或a <-1D .-1<a <34解析:∵f (x )以3为周期,所以f (2)=f (-1), 又f (x )是R 上的奇函数,∴f (-1)=-f (1),则f (2)=f (-1)=-f (1), 再由f (1)>1,可得f (2)<-1, 即3a -4a +1<-1,解得-1<a <34. 答案:D 二、填空题7.设a =3+22,b =2+7,则a ,b 的大小关系为________.解析:a =3+22,b =2+7两式的两边分别平方,可得a 2=11+46,b 2=11+47,显然,6<7.∴a <b .答案:a <b8.用反证法证明命题“若实数a ,b ,c ,d 满足a +b =c +d =1,ac +bd >1,则a ,b ,c ,d 中至少有一个是非负数”时,第一步要假设结论的否定成立,那么结论的否定是:________.解析:“至少有一个”的否定是“一个也没有”,故结论的否定是“a ,b ,c ,d 中没有一个是非负数,即a ,b ,c ,d 全是负数”.答案:a ,b ,c ,d 全是负数9.设a 、b 是两个实数,给出下列条件:①a +b >1;②a +b =2;③a +b >2;④a 2+b 2>2;⑤ab >1.其中能推出:“a 、b 中至少有一个大于1”的条件是________(填序号). 解析:若a =12,b =23,则a +b >1.但a <1,b <1,故①推不出;若a =b =1,则a +b =2,故②推不出; 若a =-2,b =-3,则a 2+b 2>2,故④推不出; 若a =-2,b =-3,则ab >1,故⑤推不出; 对于③,即a +b >2,则a 、b 中至少有一个大于1. 反证法:假设a ≤1且b ≤1,则a +b ≤2与a +b >2矛盾, 因此假设不成立,故a 、b 中至少有一个大于1. 答案:③ 三、解答题10.若a >b >c >d >0且a +d =b +c ,求证:d +a <b +c .证明:要证d +a <b +c ,只需证(d +a )2<(b +c )2,即a +d +2ad <b +c +2bc ,因a +d =b +c ,只需证ad <bc ,即ad <bc ,设a +d =b +c =t ,则ad -bc =(t -d )d -(t -c )c =(c -d )(c +d -t )<0,故ad <bc 成立,从而d +a <b +c 成立.11.已知函数y =f (x )是R 上的增函数.(1)若a ,b ∈R 且a +b ≥0,求证:f (a )+f (b )≥f (-a )+f (-b ); (2)写出(1)中的命题的逆命题,判断真假并证明你的结论. 解:(1)∵函数y =f (x )是R 上的增函数, 又∵a +b ≥0,∴a ≥-b ,b ≥-a , ∴f (a )≥f (-b ),f (b )≥f (-a ), ∴f (a )+f (b )≥f (-a )+f (-b ).(2)逆命题:若a 、b ∈R ,f (a )+f (b )≥f (-a )+f (-b ),则a +b ≥0.真命题. 证明如下:假设a +b <0,∵y =f (x )是R 上的增函数, ∴当a <-b 时,f (a )<f (-b ); 当b <-a 时,f (b )<f (-a ).∴f (a )+f (b )<f (-b )+f (-a ),与已知矛盾,∴a +b <0不成立.∴a +b ≥0.1.设非空集合M 同时满足下列两个条件:①M ⊆{1,2,3,…,n -1};②若a ∈M ,则n -a ∈M (n ≥2,n ∈N *),则下列结论正确的是( )A .若n 为偶数,则集合M 的个数为2n 2B .若n 为偶数,则集合M 的个数为2n2-1C .若n 为奇数,则集合M 的个数为2n -12 D .若n 为奇数,则集合M 的个数为2n +12解析:当n =2时,M ⊆{1},且满足1∈M,2-1∈M ,故集合M 的个数为1;当n =3时,M ⊆{1,2},且1∈M,3-1=2∈M ,故集合M 的个数为1;当n =4时,M ⊆{1,2,3},且1∈M,4-1=3∈M,2∈M,4-2=2∈M ,故集合M 的个数为3,故可排除A ,C ,D ,选B.答案:B2.设f (x )=e x -1.当a >ln2-1且x >0时,证明:f (x )>x 2-2ax . 证明:欲证f (x )>x 2-2ax ,即e x -1>x 2-2ax ,也就是e x -x 2+2ax -1>0. 可令u (x )=e x -x 2+2ax -1,则u ′(x )=e x-2x +2a . 令h (x )=e x -2x +2a ,则h ′(x )=e x-2.当x ∈(-∞,ln2)时,h ′(x )<0,函数h (x )在(-∞,ln2]上单调递减,当x ∈(ln2,+∞)时,h ′(x )>0,函数h (x )在[ln2,+∞)上单调递增.所以h (x )的最小值为h (ln2)=e ln2-2ln2+2a =2-2ln2+2a . 因为a >ln2-1,所以h (ln2)>2-2ln2+2(ln2-1)=0,即h (ln2)>0. 所以u ′(x )=h (x )>0, 即u (x )在R 上为增函数.故u (x )在(0,+∞)上为增函数.所以u (x )>u (0). 而u (0)=0,所以u (x )=e x-x 2+2ax -1>0. 即当a >ln2-1且x >0时,f (x )>x 2-2ax .。
第五节直接证明与间接证明1.直接证明——综合法、分析法内容综合法分析法定义利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立从要证明的结论出发,逐步寻求使它成立的充分条件,直到最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止思维过程由因导果(顺推证法)执果索因(逆推证法)框图表示P表示已知条件、已有的数学定义、公理、定理、性质等,Q表示所要证明的结论P⇒Q1→Q1⇒Q2→…→Q n⇒QQ⇐P1→P1⇐P2→…→得到一个明显成立的条件文字语言因为……,所以……,或由……得……,或“⇒”要证(欲证)……,只需证……,即证……2.间接证明——反证法要证明某一结论Q是正确的,但不直接证明,而是先去假设Q不成立(即Q的反面非Q 是正确的),经过正确的推理,最后得出矛盾,因此说明非Q是错误的,从而断定结论Q是正确的,这种证明方法叫做反证法.,(1)分析法的特点①当命题不知从何入手时,可以运用分析法来解决,特别是对于条件简单而结论复杂的题目,往往更是行之有效.②分析法证明过程不一定“步步可逆”,也没有必要要求“步步可逆”,因为这时仅需寻找充分条件,而不是充要条件.(2)应用反证法证题注意事项应用反证法证题时,必须先否定结论,把结论的反面作为条件,且必须根据这一条件进行推理,否则,仅否定结论,不从结论的反面出发进行推理,就不是反证法.(3)一些常见词语的否定一、判断题(对的打“√”,错的打“×”) (1)综合法是直接证明,分析法是间接证明.( )(2)分析法是从要证明的结论出发,逐步寻找使结论成立的充要条件.( ) (3)用反证法证明结论“a >b ”时,应假设“a ≤b ”.( ) (4)反证法是指将结论和条件同时否定,推出矛盾.( ) 答案:(1)× (2)× (3)√ (4)× 二、选填题1.命题“对任意角θ,cos 4θ-sin 4θ=cos 2θ”的证明:“cos 4θ-sin 4θ=(cos 2θ-sin 2θ)(cos 2θ+sin 2θ)=cos 2θ-sin 2θ=cos 2θ”过程应用了( )A .分析法B .综合法C .综合法、分析法综合使用D .间接证明法解析:选B 因为证明过程是“从左往右”,即由条件⇒结论,故选B. 2.要证a 2+b 2-1-a 2b 2≤0,只要证明( ) A .2ab -1-a 2b 2≤0B .a 2+b 2-1-a 4+b 42≤0 C.(a +b )22-1-a 2b 2≤0D .(a 2-1)(b 2-1)≥0解析:选D a 2+b 2-1-a 2b 2≤0⇔(a 2-1)(b 2-1)≥0.3.用反证法证明命题:“三角形的内角中至少有一个不大于60°”,假设正确的是( ) A .假设三个内角都不大于60° B .假设三个内角都大于60°C .假设三个内角至多有一个大于60°D .假设三个内角至多有两个大于60°解析:选B 根据反证法的定义,假设是对原命题结论的否定,故假设三个内角都大于60°.故选B.4.若2,3,x 成等比数列,则log 2x =________.解析:由题意得(3)2=2·x , 所以x =32,所以x =92.设log2x =y ,即⎝⎛⎭⎫32y =92=⎝⎛⎭⎫322, 所以y =2,即log 2x =2.答案:25.6-22与5-7的大小关系是________. 解析:假设6-22>5-7,由分析法可得, 要证 6-22>5-7,只需证 6+7>5+22, 即证13+242>13+410,即42>210. 因为42>40,所以6-22>5-7成立. 答案:6-22>5-7考点一综合法的应用[师生共研过关][典例精析]数列{a n }满足a n +1=a n2a n +1,a 1=1. (1)证明:数列⎩⎨⎧⎭⎬⎫1a n 是等差数列;(2)求数列⎩⎨⎧⎭⎬⎫1a n 的前n 项和S n ,并证明1S 1+1S 2+…+1S n>n n +1.[解] (1)证明:∵a n +1=a n2a n +1, ∴1a n +1=2a n +1a n ,化简得1a n +1=2+1a n , 即1a n +1-1a n=2, 故数列⎩⎨⎧⎭⎬⎫1a n 是以1为首项,2为公差的等差数列.(2)由(1)知1a n=2n -1,∴S n =n (1+2n -1)2=n 2.法一:1S 1+1S 2+…+1S n=112+122+…+1n 2>11×2+12×3+…+1n (n +1)=⎝⎛⎭⎫1-12+⎝⎛⎭⎫12-13+…+⎝⎛⎭⎫1n -1n +1=1-1n +1=n n +1.法二:1S 1+1S 2+…+1S n =112+122+…+1n 2>1,又∵1>n n +1,∴1S 1+1S 2+…+1S n>n n +1.[解题技法]掌握综合法证明问题的思路[过关训练]已知a ,b ,c 都为正实数,a +b +c =1.求证: (1)a +b +c ≤3; (2)13a +1+13b +1+13c +1≥32. 证明:(1)∵(a +b +c )2=(a +b +c )+2ab +2bc +2ca ≤(a +b +c )+(a +b )+(b +c )+(c +a )=3,∴a +b +c ≤3,当且仅当a =b =c =13时,等号成立.(2)∵a >0,∴3a +1>0, ∴43a +1+(3a +1)≥2 43a +1(3a +1)=4, 当且仅当43a +1=3a +1,即a =13时取“=”.∴43a +1≥3-3a ,同理得43b +1≥3-3b ,43c +1≥3-3c , 以上三式相加得4⎝⎛⎭⎫13a +1+13b +1+13c +1≥9-3(a +b +c )=6,∴13a +1+13b +1+13c +1≥32,当且仅当a=b=c=13时取“=”.考点二分析法的应用[师生共研过关][典例精析]若△ABC的三个内角A,B,C成等差数列,A,B,C的对边分别为a,b,c.求证:1a+b+1b+c=3a+b+c.[证明]要证1a+b+1b+c=3a+b+c,即证a+b+ca+b+a+b+cb+c=3,也就是证ca+b+ab+c=1,只需证c(b+c)+a(a+b)=(a+b)(b+c),需证c2+a2=ac+b2,又△ABC三内角A,B,C成等差数列,故B=60°,由余弦定理,得b2=c2+a2-2ac cos 60°,即b2=c2+a2-ac,故c2+a2=ac+b2成立.于是原等式成立.[解题技法]1.利用分析法证明问题的思路先从结论入手,由此逐步推出保证此结论成立的充分条件,而当这些判断恰恰都是已证的命题(定义、公理、定理、法则、公式等)或要证命题的已知条件时命题得证.2.分析法证明问题的适用范围当已知条件与结论之间的联系不够明显、直接,或证明过程中所需用的知识不太明确、具体时,往往采用分析法,特别是含有根号、绝对值的等式或不等式,常考虑用分析法.[过关训练]1.已知a≥b>0,求证:2a3-b3≥2ab2-a2b.证明:要证明2a3-b3≥2ab2-a2b,只需证2a3-b3-2ab2+a2b≥0,即证2a(a2-b2)+b(a2-b2)≥0,即证(a+b)(a-b)(2a+b)≥0.∵a≥b>0,∴a-b≥0,a+b>0,2a+b>0,从而(a+b)(a-b)(2a+b)≥0成立,∴2a3-b3≥2ab2-a2b.2.已知a>0,求证:a2+1a2-2≥a+1a-2.证明:要证 a 2+1a2-2≥a +1a -2,只要证a 2+1a2+2≥a +1a + 2.因为a >0,故只要证⎝⎛⎭⎫a 2+1a 2+22≥⎝⎛⎭⎫a +1a+22,即证a 2+1a 2+4 a 2+1a2+4≥a 2+2+1a2+22⎝⎛⎭⎫a +1a +2, 从而只要证2a 2+1a2≥ 2⎝⎛⎭⎫a +1a , 只要证4⎝⎛⎭⎫a 2+1a 2≥2⎝⎛⎭⎫a 2+2+1a 2,即a 2+1a 2≥2, 而上述不等式显然成立,故原不等式成立. 考点三反证法的应用[师生共研过关][典例精析]已知数列{a n }的前n 项和为S n ,且满足a n +S n =2. (1)求数列{a n }的通项公式;(2)求证:数列{a n }中不存在三项按原来顺序成等差数列. [解] (1)当n =1时,a 1+S 1=2a 1=2,则a 1=1.又a n +S n =2,所以a n +1+S n +1=2,两式相减得a n +1=12a n ,所以{a n }是首项为1,公比为12的等比数列,所以a n =12n -1.(2)证明:假设存在三项按原来顺序成等差数列,记为a p +1,a q +1,a r +1(p <q <r ,且p ,q ,r ∈N *),则2·12q =12p +12r ,所以2·2r -q =2r -p +1.(*) 又因为p <q <r , 所以r -q ∈N *,r -p ∈N *.所以(*)式左边是偶数,右边是奇数,等式不等立. 所以假设不成立,原命题得证.[解题技法]用反证法证明数学命题需把握的3点 (1)必须先否定结论,即肯定结论的反面;(2)必须从否定结论进行推理,即应把结论的反面作为条件,且必须依据这一条件进行推证;(3)推导出的矛盾可能多种多样,有的与已知矛盾,有的与假设矛盾,有的与已知事实矛盾等,但是推导出的矛盾必须是明显的.[过关训练]1.已知a1+a2+a3+a4>100,求证:a1,a2,a3,a4中至少有一个数大于25.证明:假设a1,a2,a3,a4均不大于25,即a1≤25,a2≤25,a3≤25,a4≤25,则a1+a2+a3+a4≤25+25+25+25=100,这与已知a1+a2+a3+a4>100矛盾,故假设错误.所以a1,a2,a3,a4中至少有一个数大于25.2.已知f(x)=ln(1+e x)-mx(x∈R),对于给定区间(a,b),存在x0∈(a,b),使得f(b)-f(a) b-a=f′(x0)成立,求证:x0唯一.证明:假设存在x0′∈(a,b),x0∈(a,b),且x0′≠x0,使得f(b)-f(a)b-a=f′(x0′),f(b)-f(a)b-a=f′(x0)成立,即f′(x0)=f′(x0′).因为f′(x)=e x1+e x-m,记g(x)=f′(x),所以g′(x)=e x(1+e x)2>0,f′(x)是(a,b)上的单调递增函数.所以x0=x0′,这与x0′≠x0矛盾,所以x0是唯一的.。
开卷速查(三十八) 直接证明与间接证明A级基础巩固练1.用反证法证明某命题时,对结论:“自然数a,b,c中恰有一个偶数”正确的反设为( )A.a,b,c中至少有两个偶数B.a,b,c中至少有两个偶数或都是奇数C.a,b,c都是奇数D.a,b,c都是偶数解析:“恰有一个偶数”的对立面是“没有偶数或至少有两个偶数”.答案:B2.分析法又称执果索因法,若用分析法证明:“设a>b>c,且a+b+c=0,求证b2-ac <3a”索的因应是( )A.a-b>0 B.a-c>0C.(a-b)(a-c)>0 D.(a-b)(a-c)<0解析:b2-ac<3a⇔b2-ac<3a2⇔(a+c)2-ac<3a2⇔a2+2ac+c2-ac-3a2<0⇔-2a2+ac+c2<0⇔2a2-ac-c2>0⇔(a-c)(2a+c)>0⇔(a-c)(a-b)>0.答案:C3.若P=a+a+7,Q=a+3+a+4(a≥0),则P、Q的大小关系是( )A.P>Q B.P=QC.P<Q D.由a的取值确定解析:∵要证P<Q,只要证P2<Q2,只要证:2a+7+2a a+7 <2a+7+2· a+3 a+4 ,只要证:a2+7a<a2+7a+12,只要证:0<12,∵0<12成立,∴P<Q成立.答案:C4.设x ,y ,z ∈(0,+∞),a =x +1y ,b =y +1z ,c =z +1x,则a ,b ,c 三数( )A .至少有一个不大于2B .都小于2C .至少有一个不小于2D .都大于2解析:a +b +c =x +1y +y +1z +z +1x≥6,因此a ,b ,c 至少有一个不小于2. 答案:C5.要使3a -3b <3a -b 成立,则a ,b 应满足( ) A .ab <0且a >b B .ab >0且a >b C .ab <0且a <bD .ab >0且a >b 或ab <0且a <b 解析:要使3a -3b <3a -b 成立, 只要(3a -3b )3<(3a -b )3成立, 即a -b -33a 2b +33ab 2<a -b 成立, 只要3ab 2<3a 2b 成立, 只要ab 2<a 2b 成立, 即要ab (b -a )<0成立,只要ab >0且a >b 或ab <0且a <b 成立. 答案:D6.已知a >b >0,且ab =1,若0<c <1,p =log ca 2+b 22,q =log c ⎝⎛⎭⎪⎫1a +b 2,则p 、q的大小关系是( )A .p >qB .p <qC .p =qD .p ≥q解析:∵a 2+b 22>ab =1, ∴p =log ca 2+b 22<0.又q =log c ⎝⎛⎭⎪⎫1a +b 2=log c1a +b +2ab>log c 14ab =log c 14>0,∴q >p . 答案:B7.设a =3+22,b =2+7,则a ,b 的大小关系为__________.解析:a =3+22,b =2+7两式的两边分别平方,可得a 2=11+46,b 2=11+47,显然,6<7.∴a <b . 答案:a <b8.用反证法证明命题“若实数a ,b ,c ,d 满足a +b =c +d =1,ac +bd >1,则a ,b ,c ,d 中至少有一个是非负数”时,第一步要假设结论的否定成立,那么结论的否定是__________.解析:“至少有一个”的否定是“一个也没有”,故结论的否定是“a ,b ,c ,d 中没有一个是非负数,即a ,b ,c ,d 全是负数”.答案:a ,b ,c ,d 全是负数9.设a ,b 是两个实数,给出下列条件:①a +b >1;②a +b =2;③a +b >2;④a 2+b 2>2;⑤ab >1.其中能推出:“a ,b 中至少有一个大于1”的条件是__________.(填序号) 解析:若a =12,b =23,则a +b >1,但a <1,b <1,故①推不出;若a =b =1,则a +b =2,故②推不出; 若a =-2,b =-3,则a 2+b 2>2,故④推不出; 若a =-2,b =-3,则ab >1,故⑤推不出; 对于③,即a +b >2,则a ,b 中至少有一个大于1, 反证法:假设a ≤1且b ≤1, 则a +b ≤2与a +b >2矛盾,因此假设不成立,故a ,b 中至少有一个大于1. 答案:③10.设数列{a n }是公比为q 的等比数列,S n 是它的前n 项和. (1)求证:数列{S n }不是等比数列; (2)数列{S n }是等差数列吗?为什么?解析:(1)证明:假设数列{S n }是等比数列,则S 22=S 1S 3, 即a 21(1+q )2=a 1·a 1·(1+q +q 2), 因为a 1≠0,所以(1+q )2=1+q +q 2, 即q =0,这与公比q ≠0矛盾, 所以数列{S n }不是等比数列.(2)当q =1时,S n =na 1,故{S n }是等差数列; 当q ≠1时,{S n }不是等差数列,否则2S 2=S 1+S 3, 即2a 1(1+q )=a 1+a 1(1+q +q 2), 得q =0,这与公比q ≠0矛盾.综上,当q =1时,数列{S n }是等差数列;当q ≠1时,{S n }不是等差数列.B 级 能力提升练11.如果△A 1B 1C 1的三个内角的余弦值分别等于△A 2B 2C 2的三个内角的正弦值,那么( ) A .△A 1B 1C 1和△A 2B 2C 2都是锐角三角形 B .△A 1B 1C 1和△A 2B 2C 2都是钝角三角形C .△A 1B 1C 1是钝角三角形,△A 2B 2C 2是锐角三角形D .△A 1B 1C 1是锐角三角形,△A 2B 2C 2是钝角三角形解析:由条件知,△A 1B 1C 1的三个内角的余弦值均大于0,则A 1B 1C 1是锐角三角形,假设△A 2B 2C 2是锐角三角形.由⎩⎪⎨⎪⎧sin A 2=cos A 1=sin ⎝ ⎛⎭⎪⎫π2-A 1,sin B 2=cos B 1=sin ⎝ ⎛⎭⎪⎫π2-B 1,sin C 2=cos C 1=sin ⎝ ⎛⎭⎪⎫π2-C 1,得⎩⎪⎨⎪⎧A 2=π2-A 1.B 2=π2-B 1.C 2=π2-C 1.那么A 2+B 2+C 2=π2,这与三角形内角和为180°相矛盾.所以假设不成立,又由已知可得△A 2B 2C 2不是直角三角形,所以△A 2B 2C 2是钝角三角形. 答案:D12.已知函数f (x )=⎝ ⎛⎭⎪⎫12x ,a ,b ∈R +,A =f ⎝ ⎛⎭⎪⎫a +b 2,B =f (ab ),C =f ⎝ ⎛⎭⎪⎫2ab a +b ,则A 、B 、C 的大小关系是( )A .A ≤B ≤C B .A ≤C ≤B C .B ≤C ≤AD .C ≤B ≤A解析:a +b2≥ab ≥2ab a +b ,又函数f (x )=⎝ ⎛⎭⎪⎫12x在(-∞,+∞)上是单调递减函数, ∴f ⎝⎛⎭⎪⎫a +b 2≤f (ab )≤f ⎝ ⎛⎭⎪⎫2ab a +b .答案:A13.[2015·徐州模拟]如图,AB ,CD 均为圆O 的直径,CE ⊥圆O 所在的平面,BF ∥CE ,求证:(1)平面BCEF ⊥平面ACE ; (2)直线DF ∥平面ACE .证明:(1)因为CE ⊥圆O 所在的平面,BC ⊂圆O 所在的平面,所以CE ⊥BC . 因为AB 为圆O 的直径,点C 在圆O 上, 所以AC ⊥BC .因为AC ∩CE =C ,AC ,CE ⊂平面ACE , 所以BC ⊥平面ACE . 因为BC ⊂平面BCEF , 所以平面BCEF ⊥平面ACE .(2)由(1)知AC ⊥BC ,又因为CD 为圆O 的直径,所以BD ⊥BC . 因为AC ,BC ,BD 在同一平面内,所以AC ∥BD . 因为BD ⊄平面ACE ,AC ⊂平面ACE , 所以BD ∥平面ACE .因为BF ∥CE ,同理可证BF ∥平面ACE , 因为BD ∩BF =B ,BD ,BF ⊂平面BDF , 所以平面BDF ∥平面ACE .因为DF ⊂平面BDF ,所以DF ∥平面ACE .14.已知二次函数f (x )=ax 2+bx +c (a >0)的图像与x 轴有两个不同的交点.若f (c )=0,且0<x <c 时,f (x )>0.(1)证明:1a 是函数f (x )的一个零点;(2)试比较1a与c 的大小.解析:(1)证明:∵f (x )的图像与x 轴有两个不同的交点, ∴f (x )=0有两个不等实根x 1,x 2. ∵f (c )=0,∴x 1=c 是f (x )=0的根.又x 1x 2=c a,∴x 2=1a ⎝ ⎛⎭⎪⎫1a≠c ,∴1a 是f (x )=0的一个根.即1a是函数f (x )的一个零点. (2)假设1a<c ,∵1a>0,∴由0<x <c 时,f (x )>0,知f ⎝ ⎛⎭⎪⎫1a >0,这与f ⎝ ⎛⎭⎪⎫1a=0矛盾,∴1a≥c .又∵1a ≠c ,∴1a>c .。
【步步高】2016高考数学大一轮复习 13.2直接证明与间接证明试题
理 苏教版
一、填空题
1.已知点A n (n ,a n )为函数y =x 2
+1图象上的点,B n (n ,b n )为函数y =x 图象上的点,其中n ∈N *
,设c n =a n -b n ,则c n 与c n +1的大小关系为________. 解析 由条件得c n =a n -b n =n 2
+1-n =1
n 2+1+n
,
∴c n 随n 的增大而减小.∴c n +1<c n . 答案 c n +1<c n 2.下列命题:
①三角形中至少有一个内角不小于60°; ②四面体的三组对棱都是异面直线;
③闭区间[a ,b ]上的单调函数f (x )至多有一个零点;
④设a ,b ∈Z ,若a +b 是奇数,则a ,b 中至少有一个为奇数; 其中假命题的序号是________.
解析 a +b 为奇数⇔a ,b 中有一个为奇数,另一个为偶数,故④错误. 答案 ④
3.命题“如果数列{a n }的前n 项和S n =2n 2
-3n ,那么数列{a n }一定是等差数列”是________命题(填“真”、“假”). 解析 ∵S n =2n 2
-3n ,
∴S n -1=2(n -1)2-3(n -1)(n ≥2),
∴a n =S n -S n -1=4n -5(n =1时,a 1=S 1=-1符合上式). 又∵a n +1-a n =4(n ≥1),∴{a n }是等差数列. 答案 真
4.设a ,b 是两个实数,给出下列条件:①a +b >1;②a +b =2;③a +b >2;④a 2
+b 2
>2;⑤
ab >1.
其中能推出:“a ,b 中至少有一个大于1”的条件是________.(填序号) 解析 若a =12,b =2
3,则a +b >1,但a <1,b <1,故①推不出;
若a =b =1,则a +b =2,故②推不出; 若a =-2,b =-3,则a 2
+b 2
>2,故④推不出; 若a =-2,b =-3,则ab >1,故⑤推不出; 对于③,即a +b >2,则a ,b 中至少有一个大于1,
反证法:假设a ≤1且b ≤1, 则a +b ≤2与a +b >2矛盾,
因此假设不成立,故a ,b 中至少有一个大于1. 答案 ③
5.已知函数f (x )=⎝ ⎛⎭⎪⎫12x ,a ,b 是正实数,A =f ⎝ ⎛⎭⎪⎫a +b 2,B =f (ab ),C =f ⎝ ⎛⎭
⎪
⎫2ab a +b ,则A 、B 、
C 的大小关系为________.
解析 ∵a +b
2
≥ab ≥
2ab a +b ,又f (x )=⎝ ⎛⎭
⎪⎫12x
在R 上是减函数. ∴f ⎝
⎛⎭⎪⎫a +b 2≤f (ab )≤f ⎝ ⎛⎭
⎪⎫2ab a +b .
答案 A ≤B ≤C
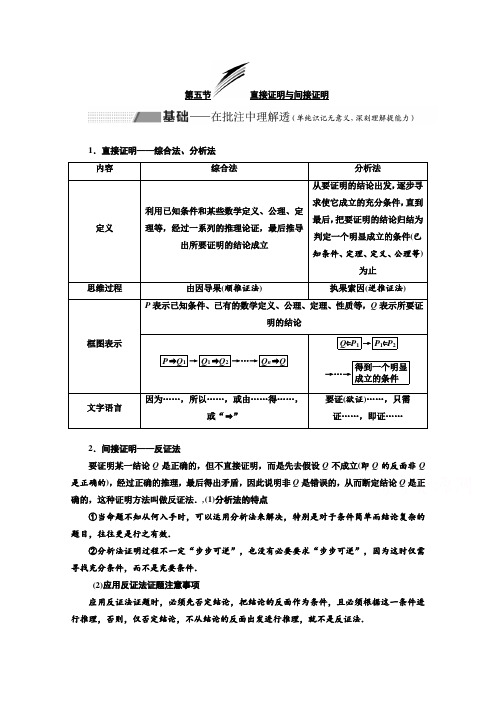
6.定义一种运算“*”:对于自然数n 满足以下运算性质: (ⅰ)1] .
解析 由(n +1)*1=n *1+1,得
n *1=(n -1)*1+1=(n -2)*1+2=…=1*1+(n -1).
又∵1*1=1,∴n *1=n . 答案 n
7.如果a a +b b >a b +b a ,则a 、b 应满足的条件是________. 解析 首先a ≥0,b ≥0且a 与b 不同为0.
要使a a +b b >a b +b a ,只需(a a +b b )2
>(a b +b a )2
,即a 3
+b 3
>a 2
b +ab 2
,只需(a +b )(a 2
-ab +b 2
)>ab (a +b ),只需a 2
-ab +b 2
>ab ,即(a -b )2
>0,只需a ≠b .故a ,b 应满足a ≥0,b ≥0且a ≠b . 答案 a ≥0,b ≥0且a ≠b
8.观察(x 2
)′=2x ,(x 4
)′=4x 3
,(cos x )′=-sin x ,由归纳推理可得:若定义在R 上
的函数f (x )满足f (-x )=f (x ),记g (x )为f (x )的导函数,则g (-x )=________. 解析 通过观察所给的结论可知,若f (x )是偶函数,则导函数g (x )是奇函数. 答案 -g (x ) 二、解答题
9.在△ABC 中,三个内角A 、B 、C 的对边分别为a 、b 、c ,若
1a +b +1b +c =3
a +
b +c
,试问A ,B ,C 是否成等差数列,若不成等差数列,请说明理由.若成等差数列,请给出证明.
解 A 、B 、C 成等差数列. 证明如下:
∵1a +b +1b +c =3a +b +c
, ∴a +b +c a +b +a +b +c
b +
c =3. ∴
c a +b +
a
b +c
=1,
∴c (b +c )+a (a +b )=(a +b )(b +c ), ∴b 2
=a 2
+c 2
-ac .
在△ABC 中,由余弦定理,得
cos B =a 2+c 2-b 22ac =ac 2ac =12
,
∵0°<B <180°,∴B =60°. ∴A +C =2B =120°. ∴A 、B 、C 成等差数列.
10.设等差数列{a n }的前n 项和为S n ,且a 5+a 13=34,S 3=9. (1)求数列{a n }的通项公式及前n 项和公式; (2)设数列{b n }的通项公式为b n =
a n
a n +t
,问是否存在正整数t ,使得b 1,b 2,b m (m ≥3,m
∈N *
)成等差数列?若存在,求出t 和m 的值;若不存在,请说明理由.
解 (1)设等差数列{a n }的公差为d ,则由⎩⎪⎨
⎪⎧
a 5+a 13=34,
3a 2=9,得⎩⎪⎨
⎪⎧
a 1+8d =17,a 1+d =3,
解得
⎩⎪⎨⎪
⎧
a 1=1,d =2,
故a n =2n -1,S n =n 2
.
(2)假设存在正整数t .由(1)知b n =2n -1
2n -1+t
,
要使b 1,b 2,b m 成等差数列; 则需2b 2=b 1+b m ,
即2×33+t =11+t +2m -12m -1+t ,整理,得m =3+4
t -1.
当t =2时,m =7;当t =3时,m =5;当t =5时,m =4. 故存在正整数t ,使得b 1,b 2,b m 成等差数列. 11.已知函数f (x )=ln x -ax 2
+(2-a )x . (1)讨论f (x )的单调性;
(2)设a >0,证明:当0<x <1a
时,f ⎝ ⎛⎭⎪⎫1a +x >f ⎝ ⎛⎭
⎪⎫1a -x ;
(3)若函数y =f (x )的图象与x 轴交于A ,B 两点,线段AB 中点的横坐标为x 0,证明:
f ′(x 0)<0.
(1)解 f (x )的定义域为(0,+∞).
f ′(x )=1
x
-2ax +(2-a )=-
2x +1 ax -1
x
.
①若a ≤0,则f ′(x )>0,∴f (x )在(0,+∞)上单调递增. ②若a >0,则由f ′(x )=0得x =1a
,且当x ∈⎝ ⎛⎭
⎪⎫0,1a 时,
f ′(x )>0;当x >1
a
时,f ′(x )<0.
∴f (x )在⎝
⎛⎭
⎪⎫0,1a 上单调递增,
在⎝ ⎛⎭
⎪⎫1a
,+∞上单调递减. (2)证明 设函数g (x )=f ⎝ ⎛⎭
⎪⎫1a
+x -f ⎝ ⎛⎭
⎪⎫1a
-x ,
则g (x )=ln(1+ax )-ln(1-ax )-2ax , g ′(x )=a 1+ax +a
1-ax -2a =2a 3x
2
1-a 2x 2.
当0<x <1
a
时,g ′(x )>0,
而g (0)=0,∴g (x )>0, 故当0<x <1a
时,f ⎝ ⎛⎭⎪⎫1a +x >f ⎝ ⎛⎭
⎪⎫1a -x .
(3)证明 由(1)可得,当a ≤0时,函数y =f (x )的图象与x 轴至多有一个交点.
∴a >0,从而f (x )的最大值为f ⎝ ⎛⎭
⎪⎫1a ,且f ⎝ ⎛⎭
⎪⎫1a >0.
不妨设A (x 1,0),B (x 2,0),0<x 1<x 2,则0<x 1<1
a
<x 2.
由(2)得f ⎝ ⎛⎭
⎪⎫2a
-x 1=f ⎝ ⎛⎭
⎪⎫1a +1a
-x 1>
f ⎣⎢⎡⎦⎥⎤
1a -⎝
⎛⎭⎪⎫1
a -x 1=f (x 1)=0. 从而x 2>2a -x 1,于是x 0=x 1+x 22>1
a .
由(1)知f ′(x 0)<0.。