条件结构(1)

条件句的种类与正确运用方法条件句是英语中的一种语法结构，用于表达一个条件与其所产生的结果之间的关系。

掌握条件句的种类与正确运用方法对于提升英语口语和写作水平非常重要。

本文将介绍常见的条件句种类，并探讨它们的正确运用方法。

一、零条件句零条件句，也称为一般条件句，用于表达某种条件下总是发生的情况。

它的结构是：If + 一般现在时，一般现在时。

例如：If it rains, the ground gets wet.（如果下雨，地面就会湿）这种条件句的使用非常普遍，用于描述客观真理或经常重复发生的事实。

二、一型条件句一型条件句用于表达可能实现的情况。

它的结构是：If + 现在时态，将来时态。

例如：If I study hard, I will pass the exam.（如果我努力学习，我就会通过考试）这种条件句通常用于表达可能实现的愿望、打算或计划。

三、二型条件句二型条件句用于表达不太可能实现的情况。

它的结构是：If + 过去时态，情态动词（could/would/might）+动词原形。

例如：If I had more money, I could buy a new car.（如果我有更多的钱，我就能买一辆新车）这种条件句通常用于表达虚拟的情况或对过去无法改变的事实进行推测。

四、三型条件句三型条件句用于表达对过去已经无法改变的情况进行的虚拟推测。

它的结构是：If + 过去完成时态，情态动词（could/would/might）+ have + 过去分词。

例如：If I had studied harder, I would have passed the exam.（如果我当时努力学习，我就能通过考试）这种条件句用于表达对过去无法改变的事实进行的虚拟推测。

正确运用条件句的方法：1. 确保条件与结果之间的关系清晰明了，避免产生歧义。

2. 根据句子的时态和情境来选择合适的条件句类型。

3. 利用条件句表达个人愿望、打算或对过去事实的猜测，以丰富语言表达。

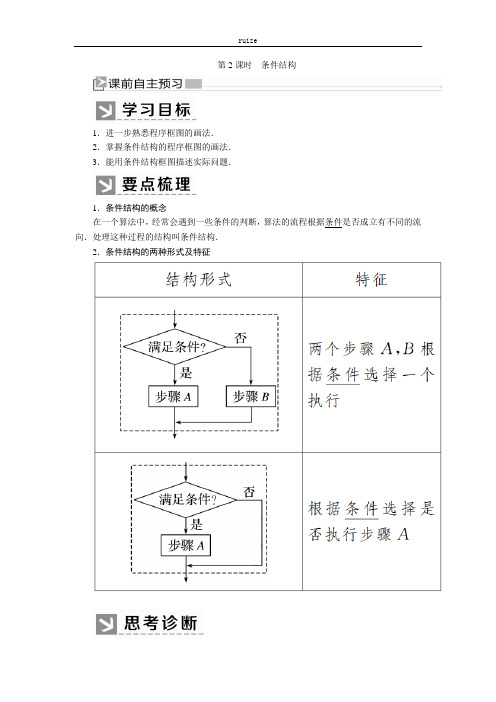
第2课时条件结构1．进一步熟悉程序框图的画法．2．掌握条件结构的程序框图的画法．3．能用条件结构框图描述实际问题．1．条件结构的概念在一个算法中，经常会遇到一些条件的判断，算法的流程根据条件是否成立有不同的流向．处理这种过程的结构叫条件结构．2．条件结构的两种形式及特征判断正误．(正确的打“√”，错误的打“×”)(1)条件结构是一种重要的基本逻辑结构，任何算法都离不开它．( )(2)条件结构中的条件需放在判断框中，判断框有两个出口，根据条件的成立与否，要走不同的出口．( )(3)条件结构中的判断框有两个出口，所以执行条件结构时的结果不唯一．( ) [提示] (1)× 有些简单的算法并不需要条件结构． (2)√ 由条件结构的特征及形式判断(2)对．(3)× 条件结构是根据条件，选择下一个执行步骤，但结果是唯一的． [★答案★] (1)× (2)√ (3)×题型一 条件结构的概念 【典例1】 (1)下列算法中，含有条件结构的是( ) A ．求两个数的积 B ．求点到直线的距离 C ．解一元二次方程D ．已知梯形两底和高求面积(2)条件结构不同于顺序结构的特征是( ) A ．处理框 B ．判断框 C ．输入、输出框 D ．起止框(3)给出以下四个问题：①输入一个数x ，输出它的绝对值； ②求面积为6的正方形的周长； ③求a ，b ，c 三个数中的最大值；④求函数f (x )＝⎩⎪⎨⎪⎧3x －1，x ≤0，x 2＋1，x >0的函数值．其中需要用条件结构来描述算法的有( ) A ．1个 B ．2个 C ．3个 D ．4个 [思路导引] 根据条件结构的概念及特征判定．[解析] (1)解一元二次方程时，当判别式Δ＜0时，方程无解，当Δ≥0时，方程有解，由于分情况，故用到条件结构．(2)在条件结构中含有判断框，而顺序结构中没有．(3)①③④都要对条件作出判断，故需要用条件结构，②用顺序结构即可． [★答案★] (1)C (2)B (3)C条件结构中含有判断框，且判断框内相应的判定条件是依据所给具体问题设定的．[针对训练1] 下列问题的算法适宜用条件结构表示的是( ) A ．求点P (2,5)到直线l ：3x －2y ＋1＝0的距离 B ．由直角三角形的两条直角边求斜边 C ．解不等式ax ＋b ＞0(其中a ≠0) D ．计算3个数的平均数[解析] 条件结构是处理逻辑判断并根据判断进行不同处理的结构，只有C 中需判断a 的符号，其余选项中都不含逻辑判断，故选C.[★答案★] C题型二简单条件结构的设计【典例2】 求过两点P 1(x 1，y 1)，P 2(x 2，y 2)的直线的斜率，设计该问题的算法并画出程序框图．[思路导引] 已知两点求直线斜率，若条件中已知x 1≠x 2，则只用顺序结构即可解决问题；若无限制条件，必须分类讨论，应用条件结构解决问题．[解] 算法如下：第一步，输入x 1，y 1，x 2，y 2， 第二步，如果x 1＝x 2，输出“斜率不存在”； 否则，k ＝y 2－y 1x 2－x 1.第三步，输出k . 程序框图如下图所示．解决这类问题时，首先对问题设置的条件作出判断，设置好判断框内的条件，然后根据条件是否成立选择不同的流向．[针对训练2]画出计算函数y＝|x－2|的函数值的程序框图．[解]算法如下：第一步，输入x.第二步，若x≥2，则y＝x－2；否则y＝2－x.第三步，输出y.程序框图如下：题型三条件结构的读图问题【典例3】(1)在如图所示的程序框图中，若a＝5，则输出b＝________.(1)题图(2)题图(2)判断正整数x的奇偶性的程序框图如图，则①处应为________(只要写出一种正确★答案★即可)．[思路导引]根据条件选择下一个执行步骤．[解析](1)因为a＝5不满足条件a>5，所以b＝52＋1＝26.(2)因为偶数除以2的余数为0，奇数除以2的余数为1，所以①处应填“r＝1？”．[★答案★](1)26(2)r＝1？(不唯一)引申探究1：本例(2)中除填r＝1？外，还可以填写怎样的条件？[解]框图的功能是判断一个数是奇数还是偶数，关键看能否被2整除，当满足条件时为奇数，不满足条件时为偶数，因此也可填写r≠0？.引申探究2：本例(2)中的程序框图中“是”改为“否”，“否”改为“是”，则①处应填什么？[解]改动后当满足条件时，x为偶数，就说明余数为0，即①处可填r＝0？或r≠1？.条件结构读图问题的两个注意点(1)理解所要实现的算法的结构特点和流程规则，分析其功能．(2)结合框图判断所要填入的内容或计算所要输出、输入的值．课堂归纳小结1．条件结构是程序框图的重要组成部分．其特点为：先判断后执行．2．在利用条件结构画程序框图时要注意两点：一是需要判断的条件是什么，二是条件判断后分别对应着执行什么.3.设计程序框图时，首先设计算法步骤，再转化为程序框图，待熟练后可以省略算法步骤直接画出程序框图．4．对于分类讨论、分段函数问题，通常设计成条件结构来解决.1.阅读如图所示的程序框图，运行相应的程序．若输入x的值为1，则输出y的值为()A．2 B．7C．8 D．128[解析]输入x＝1，因为1≥2不成立，所以y＝9－1＝8，输出y＝8.[★答案★] C2．如图是算法程序框图的一部分，其中含条件结构的是()A．①②B．①③C．②③D．①②③[解析]条件结构是处理逻辑判断并根据判别结果进行不同处理的结构，由算法程序框图可知，②③含条件结构，故选C.[★答案★] C3．如图所示的程序框图中，若输入x＝2，则输出的结果是()A．1 B．2 C．3 D．4[解析]输入x＝2后，该程序框图的执行过程是：输入x＝2，x＝2>1成立，y＝2＋2＝2，输出y＝2.[★答案★] B3题图4题图4．如图所示的程序框图，其功能是()A．输入a，b的值，按从小到大的顺序输出它们的值B．输入a，b的值，按从大到小的顺序输出它们的值C．求a，b的最大值D．求a，b的最小值[解析]输入a＝1，b＝2，运行程序框图可得输出2.根据执行过程可知该程序框图的功能是输入a，b的值，输出它们的最大值，即求a，b的最大值．[★答案★] C5．如果学生的数学成绩大于或等于120分，则输出“良好”，否则输出“一般”．用程序框图表示这一算法过程．[解]课后作业(三)(时间45分钟)学业水平合格练(时间25分钟)1．下列关于条件结构的描述，正确的是( )A ．条件结构的出口有两个，这两个出口有时可以同时执行B ．条件结构的判断框内的条件是唯一的C ．条件结构根据条件是否成立选择不同的分支执行D ．在条件结构的任何一个分支中，只能执行一个语句，而不能是多个[解析] 条件结构的两个出口不能同时执行，故A 不正确；条件结构的判断框内的条件可能有多个，不是唯一的，故B 不正确；在条件结构的任何一个分支中，可以执行多个语句，故D 不正确；故选C.[★答案★] C2．已知程序框图如图所示，则程序框图中含有的基本结构有( )A ．顺序结构B ．模块结构C ．条件结构D ．顺序结构和条件结构[解析] 由图知其中有判断框，故含有条件结构，所有的程序框图都含有顺序结构，故选D.[★答案★] D3. 某程序框图如图所示，现输入如下四个函数，则可以输出的函数是( ) A ．f (x )＝x 2B ．f (x )＝1xC ．f (x )＝ln x ＋2x －6D ．f (x )＝sin x[解析] 由框图可知函数f (x )为奇函数且存在零点，故选D. [★答案★] D3题图4题图4．上面所给程序框图，当x＝1250时输出结果为()A．20 B．25 C．30 D．40[解析]该程序框图表达的是一个分段函数输入x的值，则输出函数值f(x)，当x＝1250时，f(1250)＝1250×2%＝25.[★答案★] B5．给出以下一个算法的程序框图(如图所示)，该程序框图的功能是()A．输出a，b，c三数中的最大数B．输出a，b，c三数中的最小数C．将a，b，c按从小到大排列D．将a，b，c按从大到小排列[解析]先比较a，b的值，把较小的值赋值给a；再比较a，c的值，把较小的值赋值给a，输出a.[★答案★] B5题图 6题图6．已知y ＝|x －3|，下列程序框图表示的是给定x 值，求其相应函数值的算法．请将该程序框图补充完整，其中①处应填________；②处应填________．[解析] 因为y ＝|x －3|，所以需对x －3的正负进行判断．故判断框内应为x <3？因为“是”时，y ＝3－x .所以“否”时，x ≥3时，即y ＝x －3.[★答案★] x <3？ y ＝x －37．某算法的程序框图如图所示，若输出结果为12，则输入的实数x 的值是________．[解析] 当x ≤1时，y ＝x －1≤0， ∵输出结果为12，∴x >1，∴log 2x ＝12，∴x ＝ 2.[★答案★]28．对任意非零实数a ，b ，若a ⊗b 的运算原理如图所示，则(log 28)⊗4＝________.[解析] 因为log 28＝3，且满足3≤4，所以(log 28)⊗4＝3⊗4＝4－13＝1.[★答案★] 19．设计程序框图，输入x 的值，求函数y ＝⎩⎪⎨⎪⎧x 2，x ≥0，－x 2，x <0，的值．[解] 算法如下： 第一步，输入x 的值．第二步，判断x 的大小，若x ≥0，则y ＝x 2；否则，y ＝－x 2. 第三步，输出y 的值． 程序框图如图：10．画出解关于x 的不等式ax ＋b ＜0的程序框图． [解] 程序框图为：应试能力等级练(时间20分钟)11．某市的士收费办法如下：不超过2公里收7元(即起步价7元)，超过2公里的里程每公里收2.6元，另每车次超过2公里收燃油附加费1元(不考虑其他因素)．相应收费系统的程序框图如图所示，则①处应填( )A ．y ＝7＋2.6xB ．y ＝8＋2.6xC ．y ＝7＋2.6(x －2)D ．y ＝8＋2.6(x －2)[解析] 当x >2时，y ＝7＋2.6(x －2)＋1＝8＋2.6(x －2)，所以①处应填y ＝8＋2.6(x －2)． [★答案★] D11题图 12题图12．执行如图所示的程序框图，如果输入的t ∈[－1,3]，则输出的s 属于( )A ．[－3,4]B ．[－5,2]C ．[－4,3]D ．[－2,5][解析] 由程序框图可知，s 与t 可用分段函数表示为s ＝⎩⎪⎨⎪⎧3t ，－1≤t <1，4t －t 2，1≤t ≤3，则s ∈[－3,4]． [★答案★] A13．如图所示的程序框图，如果输入三个实数a ，b ，c ，要求输出这三个数中最大的数，那么在空白的判断框中，应该填入条件为：________.[解析] 变量x 的作用是保留3个数中的最大值，所以第二个判断框内语句为“c >x ？”，满足“是”则交换两个变量的数值，输出x 的值后结束程序，满足“否”直接输出x 的值后结束程序，故填c >x ？.[★答案★] c >x?14．定义运算a ⊗b ，运算原理如图所示，则式子4⊗1＋2⊗5的值等于________．[解析] a ⊗b ＝⎩⎪⎨⎪⎧a (b ＋1)，a ≥b ，a (b －1)，a <b ，则4⊗1＋2⊗5＝4×(1＋1)＋2×(5－1)＝16.[★答案★] 1615．如图是判断“美数”的程序框图，在[30,40]内的所有整数中“美数”的个数是多少？[解]由程序框图知“美数”是满足能被3整除不能被6整除或能被12整除的数，在[30,40]内的所有整数中，所有的能被3整除的数有30,33,36,39，共有4个数，在这四个数中能被12整除的有36，在这四个数中不能被6整除的有33,39，所以在[30,40]内的所有整数中“美数”的个数是3个．。