传递函数建模及仿真应用
- 格式:pdf
- 大小:1.25 MB
- 文档页数:3

控制系统仿真[教学目的]掌握数字仿真基本原理控制系统的数学模型建立掌握控制系统分析[教学内容]一、控制系统的数学模型sys=tf(num,den) %多项式模型,num为分子多项式的系数向量,den为分母多项式的系%数向量,函数tf()创建一个TF模型对象。
sys=zpk(z,p,k) %z为系统的零点向量,p为系统的极点向量,k为增益值,函数zpk()创建一个ZPK模型对象。
(一)控制系统的参数模型1、TF模型传递函数num=[b m b m-1 b m-2…b1 b0]den=[a m a m-1 a m-2…a1 a0]sys=tf(num,den)【例1】系统的传递函数为。
>>num=[0 1 12 44 48];>>den=[1 16 86 176 105];>>sys=tf(num,den);>>sysTransfer function:s^3 + 12 s^2 + 44 s + 48-------------------------------------s^4 + 16 s^3 + 86 s^2 + 176 s + 105>>get(sys)>>set(sys)>>set(sys,'num',[2 1 2])>> sysTransfer function:2 s^2 + s + 2-------------------------------------s^4 + 16 s^3 + 86 s^2 + 176 s + 105【例2】系统的传递函数为。
>>num=conv([20],[1 1]);>>numnum =20 20>>den=conv([1 0 0],conv([1 2],[1 6 10]));>>sys=tf(num,den)Transfer function:20 s + 20-------------------------------s^5 + 8 s^4 + 22 s^3 + 20 s^2【例3】系统的开环传递函数为,写出单位负反馈时闭环传递函数的TF模型。

如何使用MATLABSimulink进行动态系统建模与仿真如何使用MATLAB Simulink进行动态系统建模与仿真一、引言MATLAB Simulink是一款强大的动态系统建模和仿真工具,广泛应用于各个领域的工程设计和研究中。
本文将介绍如何使用MATLAB Simulink进行动态系统建模与仿真的方法和步骤。
二、系统建模1. 模型构建在MATLAB Simulink中,可以通过拖拽模块的方式来构建系统模型。
首先,将系统的元件和子系统模块从库中拖拽到模型窗口中,然后连接这些模块,形成一个完整的系统模型。
2. 参数设置对于系统模型的各个组件,可以设置对应的参数和初始条件。
通过双击模块可以打开参数设置对话框,可以设置参数的数值、初始条件以及其他相关属性。
3. 信号连接在模型中,各个模块之间可以通过信号连接来传递信息。
在拖拽模块连接的同时,可以进行信号的名称设置,以便于后续仿真结果的分析和显示。
三、系统仿真1. 仿真参数设置在进行系统仿真之前,需要设置仿真的起止时间、步长等参数。
通过点击仿真器界面上的参数设置按钮,可以进行相关参数的设置。
2. 仿真运行在设置好仿真参数后,可以点击仿真器界面上的运行按钮来开始仿真过程。
仿真器将根据设置的参数对系统模型进行仿真计算,并输出仿真结果。
3. 仿真结果分析仿真结束后,可以通过查看仿真器界面上的仿真结果来分析系统的动态特性。
Simulink提供了丰富的结果显示和分析工具,可以对仿真结果进行绘图、数据处理等操作,以便于对系统模型的性能进行评估。
四、参数优化与系统设计1. 参数优化方法MATLAB Simulink还提供了多种参数优化算法,可以通过这些算法对系统模型进行优化。
可以通过设置优化目标和参数范围,以及定义参数约束条件等,来进行参数优化计算。
2. 系统设计方法Simulink还支持用于控制系统、信号处理系统和通信系统等领域的特定设计工具。
通过这些工具,可以对系统模型进行控制器设计、滤波器设计等操作,以满足系统性能要求。
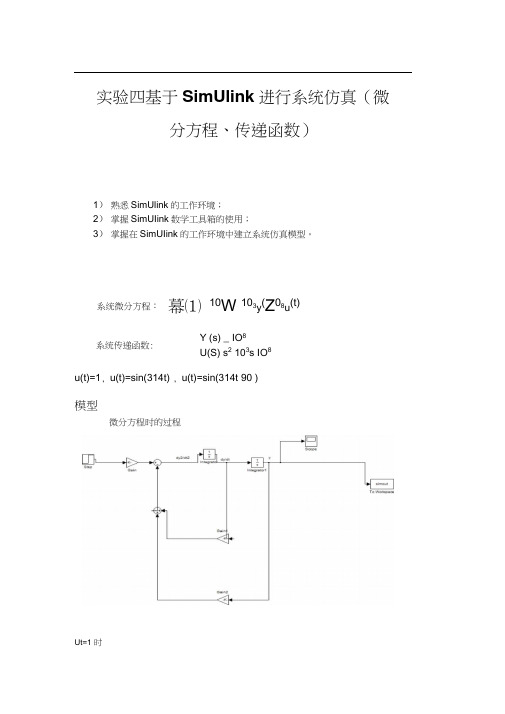
实验四基于SimUlink 进行系统仿真(微
分方程、传递函数)
1) 熟悉SimUlink 的工作环境;
2) 掌握SimUIink 数学工具箱的使用;
3) 掌握在SimUIink 的工作环境中建立系统仿真模型。
u(t)=1, u(t)=sin(314t) , u(t)=sin(314t 90°)
模型
Ut=1 时
系统微分方程:
幕⑴ 10W 103y (Z 08u (t)
Y (s) _ IO 8 U(S) s 2 103s IO 8
系统传递函数:
微分方程时的过程
u(t) =sin(314t)时
u(t) =sin(314t 90o)时
传递函数时的过程
u(t) =1时
1e8
den<s)
Sine Wave r Scop⅛5
&cop^4
u(t) =sin(314t)时
u(t) =sin(314t 90°)时
结论及感想
从两种种不同方法的仿真结果,我们可以看出分别用微分方程和传递函数在SimUIink中,仿真出来的结果没有很明显的区别,说明两种方法的精度都差不多。
但是,不同的电压源得出的仿真结果不一样,阶跃电源开始时震荡,后来幅度逐渐变小,趋近于1;正弦电源,初相不同时,初始时刻的结果也不相同,有初相时开始震荡会更剧烈,但最后都会变为稳态值,即为正弦值。
通过本次实验,我认识到了建模与仿真的一般性方法,收获甚多,也更进一步了解了
不仅仅在平时的编程方面功能强大,在仿真方面也熠熠生辉。
Matlab,Matlab。

simulink传递函数系数Simulink是一种流行的建模和仿真工具,可以用于各种应用程序的建模和仿真,包括控制器设计、信号处理、通信、器件建模等。
其中一个重要的功能就是传递函数的建模和仿真。
在Simulink中,传递函数通常表示为S函数块,其输入和输出可以是系统的状态变量、控制信号、传感器测量值等。
本文将详细讲解如何使用Simulink传递函数系数。
第一步:打开Simulink在电脑桌面上找到Simulink的图标,双击启动。
如果没有安装,则需要先安装。
第二步:添加传递函数块在Simulink的模型窗口中,可以使用鼠标从左侧的模块库中拖动传递函数块到模型中。
在传递函数块的参数设置窗口中,需要输入传递函数的系数。
通常,传递函数的系数可以由控制论或系统分析中的理论分析得到,也可以通过实验或应用经验确定。
第三步:确认传递函数块的输入和输出在传递函数块的参数设置窗口中,需要确认传递函数块的输入和输出。
传递函数的输入和输出可以是系统的状态变量、控制信号、传感器测量值等。
通常,传递函数的输入和输出应该与实际系统的输入和输出相对应。
第四步:建立完整的系统模型除了传递函数块,Simulink中的系统模型通常还包括其他类型的块,如控制器、传感器、执行器等。
在建立完整的系统模型之后,可以通过Simulink的仿真功能对这个系统模型进行仿真,并对其进行性能分析和优化。
总结:在Simulink中,传递函数系数的设置是建立模型的重要步骤之一。
通过详细的理论分析或实验确定传递函数系数可以提高模型的准确性和性能。
在建立完整的系统模型之后,可以使用Simulink 的仿真功能对模型进行性能分析和优化,并得到优秀的控制系统。

simulink传递函数单输入多输出simo 概述说明1. 引言1.1 概述在控制系统中,SIMO(Single Input Multiple Output)传递函数是一种常见的模型表示方法。
这种传递函数可以描述系统输入信号与多个输出信号之间的关系。
SIMO传递函数在实际工程中具有广泛的应用,例如机械控制系统、电力系统以及通信系统等。
本文旨在介绍SIMO传递函数的基本概念和相关应用,并重点研究Simulink在SIMO传递函数中的应用。
Simulink是一种流行的图形化仿真环境,可用于建立复杂系统的模型,并进行仿真与分析。
1.2 文章结构本文共分为五个部分,具体内容如下:第一部分为引言部分,主要介绍文章的背景和整体结构。
第二部分详细介绍SIMO传递函数,在2.1节对SIMO系统进行概述,在2.2节定义单输入多输出传递函数,并在2.3节探讨其特点与应用场景。
第三部分将重点关注Simulink在SIMO传递函数中的应用。
首先,在3.1节简要介绍Simulink软件;然后,在3.2节解释如何建立SIMO传递函数模型;最后,在3.3节探讨基于Simulink的模拟与分析方法。
第四部分将介绍SIMO传递函数模型的设计与优化方法。
具体包括参数估计与调整技术在4.1节的应用,系统辨识方法及其应用在4.2节,以及优化算法在SIMO传递函数中的应用在4.3节。
最后,第五部分为结论与展望部分。
5.1节对本文内容进行总结,5.2节展望了未来相关研究方向。
1.3 目的本文的目标是系统地介绍SIMO传递函数以及Simulink在该领域中的应用。
通过本文的阐述,读者将能够了解SIMO传递函数的概念、特点和应用,并能够掌握Simulink软件建立SIMO传递函数模型的方法和基于Simulink进行仿真与分析的技巧。
此外,本文还将介绍SIMO传递函数模型设计与优化所涉及的各种方法和算法,为读者提供理论依据和实践指导。
希望通过这篇文章,读者能够深入了解SIMO传递函数,并将其成功应用于实际工程中。

《自动控制原理》实验指导书北京科技大学自动化学院控制科学与工程系2013年4月目录实验一典型系统的时域响应和稳定性分析 (1)实验二用MATLAB建立传递函数模型 (5)实验三利用MATLAB进行时域分析 (13)实验四线性定常控制系统的稳定分析 (25)实验五利用MATLAB绘制系统根轨迹 (29)实验六线性系统的频域分析 (37)实验七基于MATLAB控制系统频域法串联校正设计 (51)附录1 MATLAB简介 (58)附录2 SIMULINK简介 (67)实验一典型系统的时域响应和稳定性分析一、实验目的1.研究二阶系统的特征参量(ξ、ωn) 对过渡过程的影响。
2.研究二阶对象的三种阻尼比下的响应曲线及系统的稳定性。
3.熟悉Routh判据,用Routh判据对三阶系统进行稳定性分析。
二、实验设备PC机一台,TD-ACC+教学实验系统一套。
三、实验原理及内容1.典型的二阶系统稳定性分析(1) 结构框图:如图1-1所示。
图1-1(2) 对应的模拟电路图:如图1-2所示。
图1-2(3) 理论分析系统开环传递函数为:G(s)=?开环增益:K=?先算出临界阻尼、欠阻尼、过阻尼时电阻R的理论值,再将理论值应用于模拟电路中,观察二阶系统的动态性能及稳定性,应与理论分析基本吻合。
在此实验中由图1-2,可以确地1-1中的参数。
0?T =, 1?T =,1?K = ?K ⇒=系统闭环传递函数为:()?W s =其中自然振荡角频率:?n ω=;阻尼比:?ζ=。
2.典型的三阶系统稳定性分析(1) 结构框图:如图1-3所示。
图1-3(2) 模拟电路图:如图1-4所示。
图1-4(3) 理论分析系统的开环传函为:()()?G s H s =系统的特征方程为:1()()0G s H s +=。
(4) 实验内容实验前由Routh 判断得Routh 行列式为:S 3 S 2 S 1 S 0为了保证系统稳定,第一列各值应为正数,因此可以确定系统稳定K值的范围系统临界稳定K系统不稳定K值的范围四、实验步骤1)将信号源单元的“ST”端插针与“S”端插针用“短路块”短接。
运算电路传递函数计算公式在电子电路中,运算电路是一种重要的电路元件,它能够对信号进行特定的数学运算,如加法、减法、乘法、除法等。
运算电路的设计和分析是电子工程师和电路设计师的重要工作之一。
在运算电路中,传递函数是一个非常重要的概念,它描述了输入信号和输出信号之间的关系。
本文将介绍运算电路传递函数的计算公式及其应用。
一、运算电路传递函数的定义。
在电子电路中,传递函数是描述电路输入和输出之间关系的重要参数。
对于运算电路而言,传递函数可以描述输入信号和输出信号之间的数学关系,通常用H(s)表示。
传递函数的计算可以通过对电路进行分析和建模来实现。
在运算电路中,传递函数通常是一个复杂的函数,它包含了电路中所有的元件和参数。
传递函数的计算是电路设计和分析的基础,对于理解电路的性能和特性具有重要意义。
二、运算电路传递函数的计算方法。
对于运算电路而言,传递函数的计算通常可以通过以下几种方法来实现:1. 传统分析法,传统分析法是一种基于电路元件参数和电路拓扑结构的传递函数计算方法。
通过对电路进行分析和建模,可以得到电路的传递函数。
这种方法需要对电路的数学模型和分析技术有较深的理解和掌握,通常适用于简单的电路和线性电路。
2. 信号流图法,信号流图法是一种图形化的传递函数计算方法,它将电路中的信号流和传递函数用图形的方式表示出来,通过对图形的分析和计算可以得到电路的传递函数。
这种方法适用于复杂的电路和非线性电路,可以直观地展现电路的传递函数和信号流动情况。
3. 模拟计算法,模拟计算法是一种基于模拟电路仿真和计算机模拟的传递函数计算方法。
通过使用电路仿真软件和计算机模拟技术,可以对电路的传递函数进行计算和分析。
这种方法适用于复杂的电路和非线性电路,可以通过计算机模拟的方式得到电路的传递函数。
以上三种方法是常用的运算电路传递函数计算方法,它们各有优缺点,可以根据具体的电路和应用需求选择合适的方法进行传递函数计算。
三、运算电路传递函数的计算公式。
实验传递函数的原理及应用1. 介绍实验传递函数是控制系统理论中的一个重要概念。
它用来描述输入信号与输出信号之间的关系,可以帮助我们研究和设计各种控制系统。
本文将介绍实验传递函数的原理及其在控制系统中的应用。
2. 实验传递函数的定义实验传递函数是一个复数函数,它将输入信号的傅立叶变换与输出信号的傅立叶变换之比定义为控制系统的传递函数。
其数学表达式可以表示为:$$ G(s) = \\frac{Y(s)}{X(s)} $$其中,G(s)表示传递函数,Y(s)表示输出信号的傅立叶变换,X(s)表示输入信号的傅立叶变换。
3. 实验传递函数的原理实验传递函数的原理基于控制系统的输入输出关系。
通过对输入信号施加一个特定的激励,观察输出信号的响应,并将它们的傅立叶变换取比值,就可以得到实验传递函数。
实验传递函数的原理可以通过以下步骤进行实现: - 施加一个特定的输入信号到控制系统; - 记录输出信号的响应; - 对输入信号和输出信号进行傅立叶变换;- 取输出信号的傅立叶变换与输入信号的傅立叶变换之比; - 将比值表示为复数函数形式,即为实验传递函数。
4. 实验传递函数的应用实验传递函数在控制系统的分析和设计中有广泛的应用。
下面列举了一些实验传递函数的应用场景:4.1 系统性能分析实验传递函数可以帮助我们分析系统的稳定性、阻尼比、共振频率等重要性能指标。
通过分析实验传递函数的零点、极点和幅频特性,可以评估系统的性能,并作出相应的控制策略。
4.2 控制系统设计实验传递函数可以用于控制系统的设计和优化。
通过理解系统的传递函数,我们可以根据系统的需求和性能指标,设计合适的控制器来实现系统的稳定性、快速响应等要求。
4.3 信号滤波实验传递函数可以用于信号的滤波。
通过选择合适的实验传递函数,可以将输入信号中的噪声和干扰滤除,得到更加稳定和准确的输出信号。
4.4 系统建模与仿真实验传递函数可以用于系统建模和仿真。
通过测量和分析实际系统的输入输出数据,可以得到系统的实验传递函数,并用于系统的仿真和预测,从而评估不同控制策略的效果。
建模建立概念关系、数学或计算机模型的过程,又称模型化,就是为了理解事物而对事物做出的一种抽象,是对事物的一种描述系统的因果关系或相互关系的过程都属于建模,所以实现这一过程的手段和方法也是多种多样的.仿真利用模型复现实际系统中发生的本质过程,并通过对系统模型的实验来研究存在的或设计中的系统,又称模拟.即模型随时间变化的实现方法。
这里所指的模型包括物理的和数学的,静态的和动态的,连续的和离散的各种模型.广义而言, 仿真是采用建模和物理的方法对客观事物进行抽象、映射、描述和复现。
建模与仿真的方法:1时间序列预测法时间序列预测法就是通过编制和分析时间序列,根据时间序列所反映出来的发展过程、方向和趋势,进行类推或延伸,借以预测下一段时间或以后若干年内可能达到的水平。
其内容包括:收集与整理某种社会现象的历史资料;对这些资料进行检查鉴别,排成数列;分析时间数列,从中寻找该社会现象随时间变化而变化的规律,得出一定的模式;以此模式去预测该社会现象将来的情况。
2定性仿真方法基于建立模型框架,对于参数采取定性处理(从一定性的约束集和一个初始状态出发预测系统未来行为)的方法.3归纳推理方法基于黑箱概念,假设对系统结构一无所知,只从系统的行为一级进行建模与仿真,根据系统观测数据,生成系统定性行为模型,用于预测系统行为.4系统动力学方法基于信息反馈及系统稳定性的概念,认为物理系统中的动力学性质及反馈控制过程在复杂系统中同样存在。
系统动力学仿真的主要目的是研究系统的变化趋势,而不注重数据的精确性.5频域建模方法频域建模方法就是从s域的传递函数G(s),根据相似原理得到与它匹配的z域传递函数G(z),从而导出其差分模型。
6图解建模图解建模法是一种采用点和线组成的、用以描述系统的图形或称图的建模方法。
图模型属于结构模型,可以用于描述自然界和人类社会中的大量事物和事物之间的关系。
在建模中采用图论作为工具。
按图的性质进行分析,为研究各种系统特别是复杂系统提供了一种有效的方法。
控制系统建模与仿真方法控制系统建模与仿真方法是现代控制系统设计和开发的基础。
通过建立准确的控制系统模型,并用仿真方法验证其性能,能够帮助工程师和设计师有效地进行控制系统的设计、调试和优化。
本文将介绍几种常见的控制系统建模与仿真方法,并探讨它们的适用范围和优缺点。
一、传递函数法传递函数法是一种基于线性时不变系统的建模方法。
它通过将控制系统表示为输入输出之间的线性关系来描述系统的动态特性。
传递函数法最适用于单输入单输出系统,并且要求系统是线性时不变的。
传递函数可以通过数学分析或实验测量来确定,其中包括系统的零点、极点和增益。
利用传递函数,可以进行频域和时域分析,评估系统的稳定性和性能,并进行控制器设计和参数调整。
二、状态空间法状态空间法是一种基于系统状态变量的建模方法。
它将系统的状态量表示为时间的函数,通过状态方程和输出方程描述系统的动态行为。
状态空间法适用于多输入多输出系统以及具有非线性和时变特性的系统。
状态空间方法可以更直观地描述系统的动态行为,并方便进行观测器设计和状态反馈控制。
此外,状态空间法还允许将系统的非线性扩展为线性模型,并通过状态反馈控制实现对非线性系统的控制。
三、仿真方法仿真方法是通过计算机模拟来模拟和评估控制系统的性能。
它可以基于建立的模型对系统的行为进行预测,并通过仿真结果来验证系统是否满足设计要求。
常见的仿真工具包括MATLAB/Simulink、LabVIEW、Python等。
这些工具提供了丰富的模型库和仿真环境,支持不同的建模方法和仿真算法。
通过仿真方法,可以进行系统特性分析、参数优化和控制器验证,大大减少了实际系统调试的时间和成本。
四、硬件在环仿真硬件在环仿真是将实际的硬件设备与仿真模型相结合,进行实时的控制系统测试和验证。
它将计算机仿真与实际硬件连接起来,通过数值计算和物理实验相结合的方式,提供了更接近实际运行条件的仿真环境。
硬件在环仿真可以有效地评估控制系统的稳定性、鲁棒性和性能,并进行实际设备的系统集成和调试。