2014届高三数学一轮复习 (教材回扣+考点分类+课堂内外+限时训练)专讲专练 2.2 函数的定义域与值域

2014届高三数学一轮复习专讲专练（教材回扣+考点分类+课堂内外+限时训练）：6.4 数列求和一、选择题1．(2013·菏泽调研)等差数列{a n }的通项公式a n ＝2n －1，数列(1a n a n ＋1)，其前n 项和为S n ，则S n 等于( )A.2n2n ＋1B.n 2n ＋1C.n2n －1D ．以上都不对解析：∵a n ＝2n －1， ∴1a n a n ＋1＝12n ＋12n －1＝12⎝ ⎛⎭⎪⎫12n －1－12n ＋1.∴S n ＝12⎝ ⎛⎭⎪⎫1－13＋13－15＋15－17＋…＋12n －1－12n ＋1＝12⎝ ⎛⎭⎪⎫1－12n ＋1＝n2n ＋1. 答案：B2．(2013·济宁月考)若数列{a n }的通项为a n ＝4n －1，b n ＝a 1＋a 2＋…＋a n n，n ∈N *，则数列{b n }的前n 项和是( )A ．n 2B ．n (n ＋1)C ．n (n ＋2)D ．n (2n ＋1)解析：a 1＋a 2＋…＋a n ＝(4×1－1)＋(4×2－1)＋…＋(4n －1)＝4(1＋2＋…＋n )－n ＝2n (n ＋1)－n ＝2n 2＋n ，∴b n ＝2n ＋1，b 1＋b 2＋…＋b n ＝(2×1＋1)＋(2×2＋1)＋…＋(2n ＋1)＝n 2＋2n ＝n (n ＋2). 答案：C3．已知数列{a n }的前n 项和S n ＝n 2－4n ＋2，则|a 1|＋|a 2|＋…＋|a 10|＝( ) A ．66 B ．65 C ．61 D ．56 解析：当n ＝1时，a 1＝S 1＝－1； 当n ≥2时，a n ＝S n －S n －1＝n 2－4n ＋2－[(n －1)2－4(n －1)＋2] ＝2n －5.∴a 2＝－1，a 3＝1，a 4＝3，…，a 10＝15. ∴|a 1|＋|a 2|＋…＋|a 10|＝1＋1＋81＋152＝2＋64＝66. 答案：A4．若S n ＝1－2＋3－4＋…＋(－1)n －1·n ，则S 17＋S 33＋S 50等于( )A ．1B ．－1C ．0D ．2解析：S n＝⎩⎪⎨⎪⎧n ＋12n 为奇数，－n2n 为偶数.故S 17＝9，S 33＝17，S 50＝－25，S 17＋S 33＋S 50＝1. 答案：A5．数列{a n }的通项公式a n ＝1n ＋n ＋2(n ∈N *)，若前n 项和为S n ，则S n 为( )A.n ＋2－1B.n ＋2＋n ＋1－2－1C.12(n ＋2－1) D.12(n ＋2＋n ＋1－2－1) 解析：∵a n ＝1n ＋n ＋2＝12(n ＋2－n )，∴S n ＝12(3－1＋4－2＋5－3＋6－4＋…＋n －n －2＋n ＋1－n －1＋n ＋2－n )＝12(－1－2＋n ＋1＋n ＋2)＝12(n ＋2＋n ＋1－2－1).答案：D6．已知数列{a n }的前n 项和S n ＝n 2－6n ，则{|a n |}的前n 项和T n ＝( ) A ．6n －n 2B ．n 2－6n ＋18C.⎩⎪⎨⎪⎧6n －n 21≤n ≤3，n 2－6n ＋18 n ＞3D.⎩⎪⎨⎪⎧6n －n 21≤n ≤3，n 2－6n n ＞3解析：由S n ＝n 2－6n ，得{a n }是等差数列，且首项为－5，公差为2. ∴a n ＝－5＋(n －1)×2＝2n －7. ∴n ≤3时，a n ＜0；n ＞3时a n ＞0.∴T n ＝⎩⎪⎨⎪⎧6n －n 21≤n ≤3，n 2－6n ＋18 n ＞3.答案：C 二、填空题7．设{a n }是等差数列，{b n }是各项都为正数的等比数列，且a 1＝b 1＝1，a 3＋b 5＝19，a 5＋b 3＝9，则数列{a n b n }的前n 项和S n ＝__________.解析：由条件易求出a n ＝n ，b n ＝2n －1(n ∈N *)．∴S n ＝1×1＋2×21＋3×22＋…＋n ×2n －1，①2S n ＝1×2＋2×22＋…＋(n －1)×2n －1＋n ×2n.②由①－②，得 －S n ＝1＋21＋22＋…＋2n －1－n ×2n，∴S n ＝(n －1)·2n＋1. 答案：(n －1)·2n＋1 8．在数列{a n }中，a n ＝1n ＋1＋2n ＋1＋…＋n n ＋1，又b n ＝2a n a n ＋1，则数列{b n }的前n 项和为__________．解析：∵a n ＝n n ＋12n ＋1＝n 2，∴b n ＝8n n ＋1＝8⎝ ⎛⎭⎪⎫1n －1n ＋1. ∴b 1＋b 2＋…＋b n ＝8⎝ ⎛⎭⎪⎫1－12＋12－13＋…＋1n －1n ＋1＝8n n ＋1.答案：8nn ＋19．若数列{a n }是正项数列，且a 1＋a 2＋…＋a n ＝n 2＋3n (n ∈N *)，则a 12＋a 23＋…＋a nn ＋1＝__________.解析：令n ＝1，得a 1＝4，∴a 1＝16.当n ≥2时，a 1＋a 2＋…＋a n －1＝(n －1)2＋3(n －1)． 与已知式相减，得a n ＝(n 2＋3n )－(n －1)2－3(n －1)＝2n ＋2.∴a n ＝4(n ＋1)2.∴n ＝1时，a 1适合a n .∴a n ＝4(n ＋1)2. ∴a nn ＋1＝4n ＋4，∴a 12＋a 23＋…＋a n n ＋1＝n 8＋4n ＋42＝2n 2＋6n .答案：2n 2＋6n 三、解答题10．设数列{a n }满足a 1＝2，a n ＋1－a n ＝3·22n －1.(1)求数列{a n }的通项公式；(2)令b n ＝na n ，求数列{b n }的前n 项和S n .解析：(1)由已知，当n ≥1时，a n ＋1＝[(a n ＋1－a n )＋(a n －a n －1)＋…＋(a 2－a 1)]＋a 1＝3(22n－1＋22n －3＋…＋2)＋2＝22(n ＋1)－1.∴当n ≥2时a n ＝22n －1，而a 1＝2，符合上式，于是数列{a n }的通项公式为a n ＝22n －1.(2)由b n ＝na n ＝n ·22n －1，知S n ＝1·2＋2·23＋3·25＋…＋n ·22n －1.①从而22·S n ＝1·23＋2·25＋3·27＋…＋n ·22n ＋1.②①－②，得(1－22)S n ＝2＋23＋25＋…＋22n －1－n ·22n ＋1.即S n ＝19[(3n －1)22n ＋1＋2]．11．已知等差数列{a n }满足a 3＝7，a 5＋a 7＝26，{a n }的前n 项和为S n . (1)求a n 及S n ； (2)令b n ＝1a 2n －1(n ∈N *)，求数列{b n }的前n 项和T n . 解析：(1)设等差数列{a n }的公差为d .因为a 3＝7，a 5＋a 7＝26，所以⎩⎪⎨⎪⎧a 1＋2d ＝7，2a 1＋10d ＝26，解得⎩⎪⎨⎪⎧a 1＝3，d ＝2.故a n ＝3＋2(n －1)＝2n ＋1，S n ＝3n ＋n n －12×2＝n 2＋2n .(2)由(1)知，a n ＝2n ＋1， 从而b n ＝1a 2n －1＝12n ＋12－1＝14·1n n ＋1＝14⎝ ⎛⎭⎪⎫1n －1n ＋1， 从而T n ＝14⎝ ⎛⎭⎪⎫1－12＋12－13＋…＋1n －1n ＋1＝14⎝ ⎛⎭⎪⎫1－1n ＋1＝n4n ＋1，即数列{b n }的前n 项和T n ＝n4n ＋1.12．已知数列{a n }是首项为a 1＝14，公比q ＝14的等比数列，设b n ＋2＝3log 14 a n (n ∈N *)，数列{c n }满足c n ＝a n ·b n .(1)求数列{b n }的通项公式； (2)求数列{c n }的前n 项和S n .解析：(1)由题意，知a n ＝⎝ ⎛⎭⎪⎫14n (n ∈N *)，又b n ＝3log 14a n －2，故b n ＝3n －2(n ∈N *)．(2)由(1)，知a n ＝⎝ ⎛⎭⎪⎫14n ，b n ＝3n －2(n ∈N *)，∴c n ＝(3n －2)×⎝ ⎛⎭⎪⎫14n (n ∈N *)．∴S n ＝1×14＋4×⎝ ⎛⎭⎪⎫142＋7×⎝ ⎛⎭⎪⎫143＋…＋(3n －5)×⎝ ⎛⎭⎪⎫14n －1＋(3n －2)×⎝ ⎛⎭⎪⎫14n，于是14S n ＝1×⎝ ⎛⎭⎪⎫142＋4×⎝ ⎛⎭⎪⎫143＋7×⎝ ⎛⎭⎪⎫144＋…＋(3n －5)×⎝ ⎛⎭⎪⎫14n ＋(3n －2)×⎝ ⎛⎭⎪⎫14n ＋1，两式相减，得34S n ＝14＋3⎣⎢⎡⎝ ⎛⎭⎪⎫142＋⎝ ⎛⎭⎪⎫143＋…⎦⎥⎤＋⎝ ⎛⎭⎪⎫14n －(3n －2)×⎝ ⎛⎭⎪⎫14n ＋1＝12－(3n ＋2)×⎝ ⎛⎭⎪⎫14n ＋1，∴S n ＝23－3n ＋23×⎝ ⎛⎭⎪⎫14n (n ∈N *)．。

2014届高三数学一轮复习专讲专练（教材回扣+考点分类+课堂内外+限时训练）：5.5 数系的扩充与复数的引入一、选择题1．(2012·安徽)复数z 满足(z －i)(2－i)＝5，则z ＝( ) A ．－2－2i B ．－2＋2i C ．2－2iD ．2＋2i解析：由(z －i)(2－i)＝5可得z －i ＝52－i ＝2＋i ，所以z ＝2＋2i.答案：D2．(2013·宝鸡质检)若复数z ＝1＋i ，i 为虚数单位，则(1＋z )·z ＝( ) A ．1＋3i B ．3＋3i C ．3－iD ．3解析：∵(1＋z )·z ＝z ＋z 2＝1＋i ＋(1＋i)2＝1＋i ＋2i ＝1＋3i. 答案：A3．若(x －i)i ＝y ＋2i ，x 、y ∈R ，则复数x ＋y i ＝( ) A ．－2＋i B ．2＋i C ．1－2iD ．1＋2i解析：由题意得，x i ＋1＝y ＋2i ，故x ＝2，y ＝1，即x ＋y i ＝2＋i. 答案：B4．(2012·山东)若复数z 满足z (2－i)＝11＋7i(i 为虚数单位)，则z 为( ) A ．3＋5i B ．3－5i C ．－3＋5iD ．－3－5i解析：由题目可知，z ＝11＋7i2－i ＝11＋7i ·2＋i 2－i ·2＋i ＝15＋25i5＝3＋5i ，故答案选A.答案：A5．(2013·荆州质检)设i 是虚数单位，复数1＋a i2－i 为纯虚数，则实数a 为( )A ．2B ．－2C ．－12D.12解析：方法一：1＋a i2－i ＝1＋a i 2－i2＋i 2＋i ＝2－a ＋2a ＋1i5为纯虚数，所以2－a ＝0，a ＝2；方法二：1＋a i 2－i ＝i a －i2－i 为纯虚数，所以a ＝2.答案：A6．(2012·课标全国)下面是关于复数z ＝2－1＋i的四个命题：p 1：|z |＝2, p 2：z 2＝2i ，p 3：z 的共轭复数为1＋i, p 4：z 的虚部为－1.其中的真命题为( ) A ．p 2，p 3 B ．p 1，p 2 C ．p 2，p 4 D ．p 3，p 4解析：因为z ＝2－1＋i＝－1－i ，所以|z |＝1＋1＝2，z 2＝(－1－i)2＝2i ，z ＝－1＋i ，z 的虚部是－1，所以p 2，p 4是真命题，所以选C.答案：C 二、填空题7．已知复数x 2－6x ＋5＋(x －2)i 在复平面内对应的点在第三象限，则实数x 的取值范围是__________．解析：∵x 为实数，∴x 2－6x ＋5和x －2都是实数．由题意，得⎩⎪⎨⎪⎧x 2－6x ＋5＜0，x －2＜0，解得⎩⎪⎨⎪⎧1＜x ＜5，x ＜2，即1＜x ＜2.故x 的取值范围是(1,2)． 答案：(1,2)8．(2012·湖南)已知复数z ＝(3＋i)2(i 为虚数单位)，则|z |＝__________. 解析：利用复数的运算法则得到z ＝8＋6i ，|z |＝82＋62＝10，所以答案为10. 答案：109．(2012·江苏)设a ，b ∈R ，a ＋b i ＝11－7i1－2i (i 为虚数单位)，则a ＋b 的值为__________．解析：因为a ＋bi ＝11－7i 1－2i ＝11－7i 1＋2i5＝5＋3i ，所以a ＝5，b ＝3，∴a ＋b＝8.答案：8 三、解答题10．已知m ∈R ，复数z ＝(m 2＋5m ＋6)＋(m 2－2m －15)i. (1)若z 与复数2－12i 相等，求m 的值；(2)若z 与复数12＋16i 互为共轭复数，求m 的值；(3)若z 对应的点在x 轴上方，求m 的取值范围．解析：(1)根据复数相等的充要条件得⎩⎪⎨⎪⎧m 2＋5m ＋6＝2，m 2－2m －15＝－12.解之得m ＝－1.(2)根据共轭复数的定义得⎩⎪⎨⎪⎧m 2＋5m ＋6＝12.m 2－2m －15＝－16.解之得m ＝1.(3)根据复数z 对应点在x 轴上方可得m 2－2m －15＞0，解之得m ＜－3或m ＞5. 11．复数z 1＝3a ＋5＋(10－a 2)i ，z 2＝21－a＋(2a －5)i ，若z 1＋z 2是实数，求实数a 的值．解析：z 1＋z 2＝3a ＋5＋(a 2－10)i ＋21－a＋(2a －5)i ＝⎝ ⎛⎭⎪⎫3a ＋5＋21－a ＋[(a 2－10)＋(2a －5)]i ＝a －13a ＋5a －1＋(a 2＋2a －15)i.∵z 1＋z 2是实数， ∴a 2＋2a －15＝0. 解得a ＝－5或a ＝3. ∵分母a ＋5≠0， ∴a ≠－5，故a ＝3.12．设复数z ＝－3cos θ＋2isin θ. (1)当θ＝43π时，求|z |的值；(2)若复数z 所对应的点在直线x ＋3y ＝0上，求2cos2θ2－12sin ⎝⎛⎭⎪⎫θ＋π4的值．解析：(1)∵θ＝43π，∴z ＝－3cos 43π＋2isin 43π＝32－3i ，∴|z |＝⎝ ⎛⎭⎪⎫322＋－32＝212. (2)由条件得－3cos θ＋3×2sin θ＝0， ∴tan θ＝12，原式＝cos θsin θ＋cos θ＝1tan θ＋1＝23.。

2014届高三数学一轮复习专讲专练（教材回扣+考点分类+课堂内外+限时训练）：2.4 函数的奇偶性与周期性一、选择题1．函数f (x )＝－x2|x ＋3|－3是( )A ．奇函数B ．偶函数C ．既是奇函数又是偶函数D ．非奇非偶函数解析：由⎩⎪⎨⎪⎧1－x 2＞0，|x ＋3|－3≠0，得－1＜x ＜1，且x ≠0.∴函数f (x )的定义域为(－1,0)∪(0,1)． ∵f (x )＝－x2|x ＋3|－3＝－x2x，∴f (－x )＝－x 2－x＝－f (x )．∴f (x )是奇函数． 答案：A2．(2012·福建)设函数D (x )＝⎩⎪⎨⎪⎧1，x 为有理数，0，x 为无理数，则下列结论错误的是( )A ．D (x )的值域为{0,1}B ．D (x )是偶函数C ．D (x )不是周期函数D ．D (x )不是单调函数解析：显然A ，D 是对的．若x 是无理数，所以－x 也是无理数；若x 是有理数，则－x 也是有理数，则D (－x )＝D (x )，所以D (x )是偶函数，B 对．对于任意有理数T ，f (x ＋T )＝f (x )(若x 是无理数，则x ＋T 也是无理数；若x 是有理数，则x ＋T 也是有理数)，故C 不对．答案：C3．(2012·山东)定义在R 上的函数f (x )满足f (x ＋6)＝f (x )．当－3≤x ＜－1时，f (x )＝－(x ＋2)2，当－1≤x ＜3时，f (x )＝x .则f (1)＋f (2)＋f (3)＋…＋f (2 012)＝( )A ．335B ．338C ．1 678D ．2 012解析：由f (x ＋6)＝f (x )可知函数是周期为6的周期函数，又因为当－3≤x ＜－1时，f (x )＝－(x ＋2)2，当－1≤x ＜3时，f (x )＝x 可知，f (1)＝1，f (2)＝2，f (3)＝f (－3)＝－(－3＋2)2＝－1，f (4)＝f (－2)＝－(－2＋2)2＝0，f (5)＝f (－1)＝－1，f (6)＝f (0)＝0，故而f (1)＋f (2)＋f (3)＋f (4)＋f (5)＋f (6)＝1，故而f (1)＋f (2)＋f (3)＋…＋f (2 012)＝335×1＋f (1)＋f (2)＝338.答案：B4．已知定义在R 上的奇函数f (x )满足f (x －4)＝－f (x )，且在区间[0,2]上是增函数，则( )A ．f (－25)＜f (11)＜f (80)B ．f (80)＜f (11)＜f (－25)C ．f (11)＜f (80)＜f (－25)D ．f (－25)＜f (80)＜f (11)解析：由函数f (x )是奇函数且f (x )在[0,2]上是增函数可以推知，f (x )在[－2,2]上递增，又f (x －4)＝－f (x )⇒f (x －8)＝－f (x －4)＝f (x )，故函数f (x )以8为周期，f (－25)＝f (－1)，f (11)＝f (3)＝－f (3－4)＝f (1)，f (80)＝f (0)，故f (－25)＜f (80)＜f (11)．故选D.答案：D5．(2013·太原五中月考)若函数f (x )、g (x )分别是R 上的奇函数、偶函数，且满足f (x )－g (x )＝e x，则有( )A ．f (2)＜f (3)＜g (0)B ．g (0)＜f (3)＜f (2)C ．f (2)＜g (0)＜f (3)D ．g (0)＜f (2)＜f (3)解析：由题意，得⎩⎪⎨⎪⎧f x －g x ＝e x，－f x －g x ＝e －x ，解得⎩⎪⎨⎪⎧f x ＝e x －e －x2，gx ＝－e x＋e－x2.故g (0)＝－1，f (x )为R 上的增函数，0＜f (2)＜f (3)，故g (0)＜f (2)＜f (3).答案：D6．(2013·曲阜师大附中质检)若偶函数y ＝f (x )对任意实数x 都有f (x ＋1)＝－f (x )，且在[0,1]上单调递减，则( )A ．f ⎝ ⎛⎭⎪⎫72＜f ⎝ ⎛⎭⎪⎫73＜f ⎝ ⎛⎭⎪⎫75B ．f ⎝ ⎛⎭⎪⎫75＜f ⎝ ⎛⎭⎪⎫72＜f ⎝ ⎛⎭⎪⎫73C ．f ⎝ ⎛⎭⎪⎫73＜f ⎝ ⎛⎭⎪⎫72＜f ⎝ ⎛⎭⎪⎫75D ．f ⎝ ⎛⎭⎪⎫75＜f ⎝ ⎛⎭⎪⎫73＜f ⎝ ⎛⎭⎪⎫72 解析：由f (x ＋1)＝－f (x )，知f (x )是周期函数，且最小正周期为2.故f ⎝ ⎛⎭⎪⎫72＝f ⎝ ⎛⎭⎪⎫4－12＝f ⎝ ⎛⎭⎪⎫－12＝f ⎝ ⎛⎭⎪⎫12，f ⎝ ⎛⎭⎪⎫73＝f ⎝ ⎛⎭⎪⎫2＋13＝f ⎝ ⎛⎭⎪⎫13， f ⎝ ⎛⎭⎪⎫75＝f ⎝⎛⎭⎪⎫－2＋75＝f ⎝ ⎛⎭⎪⎫－35＝f ⎝ ⎛⎭⎪⎫35. 又因为35＞12＞13，所以f ⎝ ⎛⎭⎪⎫75＜f ⎝ ⎛⎭⎪⎫72＜f ⎝ ⎛⎭⎪⎫73. 答案：B 二、填空题7．(2012·上海)已知y ＝f (x )＋x 2是奇函数，且f (1)＝1，若g (x )＝f (x )＋2，则g (－1)＝__________.解析：令h (x )＝f (x )＋x 2，∴h (1)＝f (1)＋1＝2.h (－1)＝f (－1)＋1＝－2，∴f (－1)＝－3，∴g (－1)＝f (－1)＋2＝－1. 答案：－18．(2013·银川质检)已知f (x )是定义在(－3,3)上的奇函数，当0＜x ＜3时，f (x )的图像如图所示，那么不等式xf (x )＜0的解集为__________．解析：当0＜x ＜3时，由图像知，满足xf (x )＜0的解为： 0＜x ＜1，由奇函数的对称性可求. 答案：(－1,0)∪(0,1)9．(2012·江苏)设f (x )是定义在R 上且周期为2的函数，在区间[－1,1]上，f (x )＝⎩⎪⎨⎪⎧ax ＋1，－1≤x ＜0bx ＋2x ＋1，0≤x ≤1，其中a ，b ∈R ，若f ⎝ ⎛⎭⎪⎫12＝f ⎝ ⎛⎭⎪⎫32，则a ＋3b 的值为______________．解析：由题意得，f (12)＝f (32)＝f (－12)，所以b2＋232＝－12a ＋1，∴32a ＋b ＝－1.①又f (－1)＝f (1)，∴b ＝－2a .② 解①②得a ＝2，b ＝－4，∴a ＋3b ＝－10. 答案：－10 三、解答题10．(2013·曲阜师大附中质检)定义域为[－1,1]的奇函数f (x )满足f (x )＝f (x －2)，且当x ∈(0,1)时，f (x )＝2x ＋x .(1)求f (x )在[－1,1]上的解析式； (2)求函数f (x )的值域．解析：(1)当x ＝0时，f (0)＝－f (0)，故f (0)＝0. 当x ∈(－1,0)时，－x ∈(0,1)，f (x )＝－f (－x )＝－(－2x ＋－x )＝2x －－x .若x ＝－1时，f (－1)＝－f (1)．又f (1)＝f (1－2)＝f (－1)，故f (1)＝－f (1)，得f (1)＝0，从而f (－1)＝－f (1)＝0.综上，f (x )＝⎩⎨⎧2x －－x ，x ∈－1，，0， x ＝0，±1，2x ＋x ， x ∈，(2)∵x ∈(0,1)时，f (x )＝2x ＋x ，∴f ′(x )＝2＋12x ＞0，故f (x )在(0,1)上单调递增．∴f (x )∈(0,3)．∵f (x )是定义域为[－1,1]上的奇函数， ∴当x ∈[－1,1]时，f (x )∈(－3,3)． ∴f (x )的值域为(－3,3)．11．(2013·舟山调研)已知函数f (x )＝x 2＋a x(x ≠0，常数a ∈R )． (1)讨论函数f (x )的奇偶性，并说明理由；(2)若函数f (x )在x ∈[2，＋∞)上为增函数，求a 的取值范围．解析：(1)当a ＝0时，f (x )＝x 2，对任意的x ∈(－∞，0)∪(0，＋∞)，f (－x )＝(－x )2＝x 2＝f (x )，∴f (x )为偶函数．当a ≠0时，f (x )＝x 2＋a x(a ≠0，x ≠0)， 取x ＝±1，得f (－1)＋f (1)＝2≠0，f (－1)－f (1)＝－2a ≠0，∴f (－1)≠－f (1)，f (－1)≠f (1)． ∴函数f (x )既不是奇函数，也不是偶函数．(2)方法一：要使函数f (x )在x ∈[2，＋∞)上为增函数， 等价于f ′(x )≥0在x ∈[2，＋∞)上恒成立， 即f ′(x )＝2x －a x2≥0在x ∈[2，＋∞)上恒成立． 故a ≤2x 3在x ∈[2，＋∞)上恒成立． ∴a ≤(2x 3)min ＝16.∴a 的取值范围是(－∞，16]． 方法二：设2≤x 1＜x 2，则f (x 1)－f (x 2)＝x 21＋a x 1－x 22－a x 2＝x 1－x 2x 1x 2[x 1x 2(x 1＋x 2)－a ]． 要使函数f (x )在x ∈[2，＋∞)上为增函数，必须f (x 1)－f (x 2)＜0恒成立． ∵x 1－x 2＜0，x 1x 2＞0，即a ＜x 1x 2(x 1＋x 2)恒成立， 又∵x 1＋x 2＞4，x 1x 2＞4， ∴x 1x 2(x 1＋x 2)＞16.∴a 的取值范围是(－∞，16]．12．(2013·沈阳质检)设f (x )是(－∞，＋∞)上的奇函数，f (x ＋2)＝－f (x )，当0≤x ≤1时，f (x )＝x .(1)求f (π)的值；(2)当－4≤x ≤4时，求f (x )的图像与x 轴所围成图形的面积； (3)写出(－∞，＋∞)内函数f (x )的单调增(或减)区间．解析：(1)由f (x ＋2)＝－f (x )得，f (x ＋4)＝f [(x ＋2)＋2]＝－f (x ＋2)＝f (x )， 所以f (x )是以4为周期的周期函数． ∴f (π)＝f (－1×4＋π)＝f (π－4) ＝－f (4－π) ＝－(4－π) ＝π－4.(2)由f (x )是奇函数与f (x ＋2)＝－f (x )，得：f [(x －1)＋2]＝－f (x －1)＝f [－(x －1)]，即f (1＋x )＝f (1－x )．故知函数y ＝f (x )的图像关于直线x ＝1对称．又0≤x ≤1时，f (x )＝x ，且f (x )的图像关于原点成中心对称，则f (x )的图像如图所示．当－4≤x ≤4时，f (x )的图像与x 轴围成的图形面积为S ，则S ＝4S △OAB ＝4×⎝ ⎛⎭⎪⎫12×2×1＝4.(3)函数f (x )的单调递增区间为[4k －1,4k ＋1](k ∈Z )，单调递减区间为[4k ＋1,4k ＋3](k ∈Z )．。

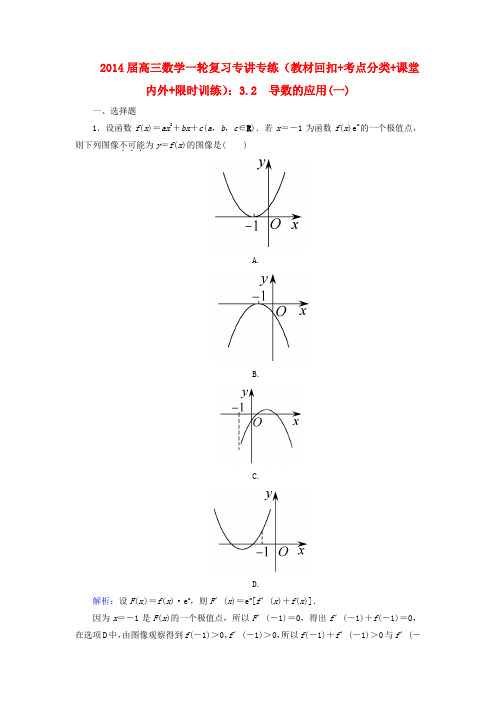
2014届高三数学一轮复习专讲专练（教材回扣+考点分类+课堂内外+限时训练）：3.2 导数的应用(一)一、选择题1．设函数f(x)＝ax2＋bx＋c(a，b，c∈R)．若x＝－1为函数f(x)e x的一个极值点，则下列图像不可能．．．为y＝f(x)的图像是( )A.B.C.D.解析：设F(x)＝f(x)·e x，则F′(x)＝e x[f′(x)＋f(x)]．因为x＝－1是F(x)的一个极值点，所以F′(－1)＝0，得出f′(－1)＋f(－1)＝0，在选项D中，由图像观察得到f(－1)＞0，f′(－1)＞0，所以f(－1)＋f′(－1)＞0与f′(－1)＋f (－1)＝0矛盾，故选D.答案：D2．若a ＞0，b ＞0，且函数f (x )＝4x 3－ax 2－2bx ＋2在x ＝1处有极值，则ab 的最大值等于( )A ．2B ．3C ．6D ．9 解析：∵f ′(x )＝12x 2－2ax －2b ， ∵Δ＝4a 2＋96b ＞0，又x ＝1是极值点， ∴f ′(1)＝12－2a －2b ＝0，即a ＋b ＝6. ∴ab ≤a ＋b24＝9，当且仅当a ＝b 时“＝”成立，所以ab 的最大值为9，故选D.答案：D3．(2013·济宁模拟)若函数f (x )＝x 3－6bx ＋3b 在(0,1)内有极小值，则实数b 的取值范围是( )A ．(0,1)B ．(－∞，1)C ．(0，＋∞)D.⎝ ⎛⎭⎪⎫0，12 解析：由f ′(x )＝3x 2－6b ＝0，得x ＝±2b (b ＞0)， ∴0＜2b ＜1，∴0＜b ＜12.答案：D4．已知对任意实数x ，都有f (－x )＝－f (x )，g (－x )＝g (x )，且x ＞0时，f ′(x )＞0，g ′(x )＞0，则x ＜0时( )A ．f ′(x )＞0，g ′(x )＞0B ．f ′(x )＞0，g ′(x )＜0C ．f ′(x )＜0，g ′(x )＞0D ．f ′(x )＜0，g ′(x )＜0解析：由题意知，f (x )是奇函数，g (x )是偶函数，x ＞0时，f ′(x )＞0，g ′(x )＞0，即x ＞0时，f (x )是增函数，g (x )是增函数，所以x ＜0时，f (x )是增函数，g (x )是减函数，即x ＜0时，f ′(x )＞0，g ′(x )＜0.答案：B5．(2013·德州联考)已知y ＝f (x )是定义在R 上的函数，且f (1)＝1，f ′(x )＞1，则f (x )＞x 的解集是( )A ．(0,1)B ．(－1,0)∪(0,1)C ．(1，＋∞)D ．(－∞，－1)∪(1，＋∞)解析：令F (x )＝f (x )－x ，则F ′(x )＝f ′(x )－1＞0，所以F (x )是增函数，故易得F (x )＞F (1)的解集，即f (x )＞x 的解集是(1，＋∞).答案：C6．(2013·烟台质检)已知函数f (x )＝4x ＋3sin x ，x ∈(－1,1)，如果f (1－a )＋f (1－a 2)＜0成立，则实数a 的取值范围为( )A ．(0,1)B ．(1，2)C ．(－2，－2)D ．(－∞，－2)∪(1，＋∞)解析：∵f (x )＝4x ＋3sin x ，x ∈(－1,1)， ∴f ′(x )＝4＋3cos x ＞0在x ∈(－1,1)上恒成立． ∴f (x )在(－1,1)上是增函数．又f (x )＝4x ＋3sin x ，x ∈(－1,1)是奇函数，∴不等式f (1－a )＋f (1－a 2)＜0可化为f (1－a )＜f (a 2－1)． 从而可知，a 需满足⎩⎪⎨⎪⎧－1＜1－a ＜1，－1＜a 2－1＜1，1－a ＜a 2－1，解得1＜a ＜ 2.答案：B 二、填空题7．若函数y ＝a (x 3－x )在区间⎝ ⎛⎭⎪⎫－33，33上为减函数，则a 的取值范围是__________． 解析：y ′＝a (3x 2－1)，∵函数在⎝ ⎛⎭⎪⎫－33，33上为减函数， ∴y ′≤0在⎝ ⎛⎭⎪⎫－33，33上恒成立．∵3x 2－1＜0，∴a ≥0. 当a ＝0时，函数为常数函数，不合题意，∴a ＞0. 答案：a ＞08．已知函数f (x )＝x 3－3a 2x ＋a (a ＞0)的极大值为正数，极小值为负数，则a 的取值范围是__________．解析：f ′(x )＝3x 2－3a 2＝3(x ＋a )(x －a )，由f ′(x )＜0，得－a ＜x ＜a .∴f (x )在区间(－∞，－a )内递增，在区间[－a ，a ]内递减，在区间[a ，＋∞)内递增，极大值为f (－a )＝2a 3＋a ＝a (2a 2＋1)＞0，①极小值为f (a )＝a (1－2a 2)＜0，② 由①②得a ∈⎝ ⎛⎭⎪⎫22，＋∞. 答案：⎝⎛⎭⎪⎫22，＋∞ 9．(2013·绵阳模拟)下图是函数y ＝f (x )的导函数的图像，给出下面四个判断．①f (x )在区间[－2，－1]上是增函数； ②x ＝－1是f (x )的极小值点；③f (x )在区间[－1,2]上是增函数，在区间[2,4]上是减函数； ④x ＝3是f (x )的极小值点．其中，所有正确判断的序号是__________． 解析：由函数y ＝f (x )的导函数的图像可知：(1)f (x )在区间[－2，－1]上是减函数，在[－1,2]上为增函数，在[2,4]上为减函数； (2)f (x )在x ＝－1处取得极小值，在x ＝2处取得极大值． 故②③正确． 答案：②③ 三、解答题10．设a ＞0，讨论函数f (x )＝ln x ＋a (1－a )x 2－2(1－a )x 的单调性． 解析：由题意知x ＞0.当a ＝1时，f (x )＝ln x ，其在(0，＋∞)上为增函数． 当a ≠1时，f ′(x )＝1x＋2a (1－a )x －2(1－a )＝2a －a x 2－－a x ＋1x，令f ′(x )＝0得2a (1－a )x 2－2(1－a )x ＋1＝0. 由Δ＝4(1－a )2－8a (1－a )＝0得a ＝13.(1)当0＜a ＜13时，2a (1－a )x 2－2(1－a )x ＋1＝0的判别式Δ＞0，两根分别为x 1＝1－a －－a －3a 2a －a ，x 2＝1－a ＋－a －3a2a －a.又[－a－3a]2－(1－a )2＝2a (a －1)＜0，所以x 1＞0且x 2＞x 1.所以当0＜x ＜x 1或x ＞x 2时，f ′(x )＞0；当x 1＜x ＜x 2时，f ′(x )＜0.f (x )在⎝⎛⎭⎪⎫0，1－a －－a －3a2a －a ， ⎝⎛⎭⎪⎫1－a ＋－a －3a2a －a ，＋∞上为增函数， 在⎝⎛⎭⎪⎫1－a －－a －3a2a －a ，1－a ＋－a －3a 2a －a上为减函数． (2)当a ＝13时，f ′(x )≥0，f (x )在(0，＋∞)上为增函数．(3)当13＜a ＜1时，f ′(x )＞0，f (x )在(0，＋∞)上为增函数．(4)当a ＞1时，x 1＞0，x 2＝1－a ＋－a －3a 2a －a ＝a －1－－a －3aa －a＜0，故当0＜x ＜x 1时，f ′(x )＞0；当x ＞x 1时，f ′(x )＜0.f (x )在⎝⎛⎭⎪⎫0，1－a －－a －3a2a －a上为增函数， 在⎝⎛⎭⎪⎫1－a －－a －3a2a －a ，＋∞上为减函数．综上可知：(1)当0＜a ＜13时，f (x )在⎝ ⎛⎭⎪⎫0，1－a －－a －3a2a －a ，⎝⎛⎭⎪⎫1－a ＋－a －3a2a －a ，＋∞上为增函数，在 ⎝⎛⎭⎪⎫1－a －－a －3a2a －a ，1－a ＋－a －3a 2a －a上为减函数； (2)当13≤a ≤1时，f (x )在(0，＋∞)上为增函数；(3)当a ＞1时，f (x )在⎝⎛⎭⎪⎫0，1－a －－a－3a2a －a上为增函数，在⎝⎛⎭⎪⎫1－a －－a －3a2a －a ，＋∞上为减函数．11．设f (x )＝ex1＋ax 2，其中a 为正实数．(1)当a ＝43时，求f (x )的极值点；(2)若f (x )为R 上的单调函数，求a 的取值范围． 解析：对f (x )求导得f ′(x )＝e x1＋ax 2－2ax＋ax.①(1)当a ＝43时，令f ′(x )＝0，则4x 2－8x ＋3＝0，解得x 1＝32，x 2＝12.综合①，可知所以，x 1＝2是极小值点，x 2＝2是极大值点．(2)若f (x )为R 上的单调函数，则f ′(x )在R 上不变号，结合①与条件a ＞0，知ax2－2ax ＋1≥0在R 上恒成立，因此Δ＝4a 2－4a ＝4a (a －1)≤0，由此并结合a ＞0，知0＜a ≤1.12．(2013·安徽名校联考)函数f (x )＝ax 2＋2x ＋1，g (x )＝ln x . (1)设F (x )＝f (x )－g (x )，求F (x )有两个极值点的充要条件； (2)求证：当a ≥0时，不等式f (x )≥g (x )恒成立． 解析：(1)函数f (x )＝ax 2＋2x ＋1，g (x )＝ln x .∴F (x )＝f (x )－g (x )＝ax 2＋2x ＋1－ln x ，其定义域为(0，＋∞)． ∴F ′(x )＝2ax ＋2－1x ＝2ax 2＋2x －1x.∴F (x )有两个极值点⇔方程2ax 2＋2x －1＝0有两个不等正根．即⎩⎪⎨⎪⎧Δ＝4＋8a ＞0，x 1＋x 2＝－1a ＞0，x 1·x 2＝－12a＞0⇒－12＜a ＜0.∴F (x )有两个极值点的充要条件是－12＜a ＜0.(2)不等式f (x )≥g (x )恒成立⇔F (x )＝ax 2＋2x ＋1－ln x ≥0在(0，＋∞)上恒成立，即a ≥ln x －x ＋x2在(0，＋∞)上恒成立，令h (x )＝ln x －(2x ＋1)．h ′(x )＝1x －2＝1－2x x ，当x ∈⎝ ⎛⎭⎪⎫0，12时，h ′(x )＞0. 当x ∈⎝ ⎛⎭⎪⎫12，＋∞时，h ′(x )＜0.∴x ＝12时，h (x )max ＝ln 12－2＜0.故x ∈(0，＋∞)，都有ln x －x ＋x2＜0.所以当a ≥0时，a ≥ln x －x ＋x2在(0，＋∞)上恒成立．即不等式f (x )≥g (x )在(0，＋∞)上恒成立．。

2014届高三数学一轮复习专讲专练（教材回扣+考点分类+课堂内外+限时训练）：2.7 对数与对数函数一、选择题1．(2013·日照联考)设函数f (x )＝log 2x 的反函数为y ＝g (x )，若g ⎝ ⎛⎭⎪⎫1a －1＝14，则a等于( )A ．－2B ．－12C.12D ．2解析：因为函数f (x )＝log 2x 的反函数为y ＝2x，所以g (x )＝2x，由g ⎝ ⎛⎭⎪⎫1a －1＝14，得21a －11a --1＝14.所以1a －1＝－2，a ＝12. 答案：C2．已知函数f (x )＝a x＋log a x (a ＞0，且a ≠1)在[1,2]上的最大值与最小值之和为l og a 2＋6，则a 的值为( )A.12B.14 C ．2D ．4解析：由题可知函数f (x )＝a x＋log a x 在[1,2]上是单调函数，所以其最大值与最小值之和为f (1)＋f (2)＝a ＋log a 1＋a 2＋log a 2＝log a 2＋6，整理可得a 2＋a －6＝0，解得a ＝2或a ＝－3(舍去)，故a ＝2.答案：C3．若0＜a ＜1，x ＝log a 2＋log a 3，y ＝12log a 5，z ＝log a 21－log a 3，则( )A ．x ＞y ＞zB ．z ＞y ＞xC ．y ＞x ＞zD ．z ＞x ＞y解析：x ＝log a 6，y ＝log a 5，z ＝log a 7.因为0＜a ＜1，所以y ＝log a x 在(0，＋∞)上是减函数． 又7＞6＞5，故y ＞x ＞z .选C. 答案：C4．已知lg a ＋lg b ＝0(a ＞0，b ＞0且a ≠1，b ≠1)，则函数f (x )＝a x与函数g (x )＝－log b x 的图像可能是( )A ． B.C ． D.解析：由lg a ＋lg b ＝0(a ＞0，b ＞0，且a ≠1，b ≠1)，得ab ＝1.若a ＞1，则0＜b ＜1，而y ＝－log b x 的图像与y ＝log b x 的图像关于x 轴对称，故选B. 答案：B5．已知函数f (x )＝⎝ ⎛⎭⎪⎫13x－log 2x ，实数a ，b ，c 满足f (a )·f (b )·f (c )＜0(0＜a ＜b ＜c )，若实数x 0为方程f (x )＝0的一个解，那么下列不等式中，不可能．．．成立的是( ) A ．x 0＜a B ．x 0＞b C ．x 0＜cD ．x 0＞c解析：易知f (x )在(0，＋∞)上是减函数．由0＜a ＜b ＜c ，知f (a )＞f (b )＞f (c )． 又f (a )·f (b )·f (c )＜0，故f (c )＜0，从而f (a )·f (b )＞0.又f (x )的图像在(0，＋∞)上是一条连续不断的曲线，故x 0＞c 不可能成立．选D. 答案：D6．已知函数f (x )＝log 2(a －2x)＋x －2，若f (x )＝0有解，则实数a 的取值范围是( ) A ．(－∞，－4]∪[4，＋∞) B ．[1，＋∞) C ．[2，＋∞) D ．[4，＋∞)解析：方法一：f (x )＝log 2(a －2x )＋x －2＝0，得a －2x ＝22－x，即a －2x ＝42x ，令t ＝2x(t＞0)，则t 2－at ＋4＝0在t ∈(0，＋∞)上有解，令g (t )＝t 2－at ＋4，g (0)＝4＞0，故满足⎩⎪⎨⎪⎧a 2＞0，Δ＝a 2－16≥0，得a ≥4.方法二：f (x )＝l og 2(a －2x )＋x －2＝0，得a －2x ＝22－x，a ＝2x＋42x ≥4.答案：D 二、填空题7．(2013·金华联考)已知函数f (x )＝log 2(x 2－ax ＋a 2)的图像关于x ＝2对称，则a 的值为__________．解析：由题意f (x )＝f (4－x )，∴x 2－ax ＋a 2＝(4－x )2－a (4－x )＋a 2，整理得a ＝4. 答案：48．(2013·杭州月考)设f (x )＝11＋2lg x ＋11＋4lg x ＋11＋8lg x ，则f (x )＋f ⎝ ⎛⎭⎪⎫1x ＝__________. 解析：f (x )＋f ⎝ ⎛⎭⎪⎫1x ＝⎝ ⎛⎭⎪⎫11＋2lg x ＋11＋4lg x ＋11＋8lg x ＋⎝ ⎛⎭⎪⎫2lg x 1＋2lg x ＋4lg x 1＋4lg x ＋8lg x1＋8lg x ＝3.答案：39．(2013·湖南联考)已知f (x )是定义在R 上的奇函数，且f (x ＋2)＋f (x )＝0，当x ∈[0,1]时，f (x )＝2x－1，则f (log 18125)＝__________.解析：f (x )是定义在R 上的奇函数，且f (x ＋2)＋f (x )＝0，f (log 18 125)＝f (－log 25)＝－f (log 25)＝f (log 25－2)＝2log 25－2－1＝54－1＝14.答案：14三、解答题10．若f (x )＝x 2－x ＋b ，且f (log 2a )＝b ，log 2f (a )＝2(a ≠1)． (1)求f (log 2x )的最小值及相应的x 值；(2)x 取何值时，f (log 2x )＞f (1)，且log 2f (x )＜f (1)． 解析：(1)∵f (x )＝x 2－x ＋b . ∴f (log 2a )＝(log 2a )2－log 2a ＋b ， 由已知(log 2a )2－log 2a ＋b ＝b ， ∴log 2a (log 2a －1)＝0.∵a ≠1，∴log 2a ＝1. ∴a ＝2.又log 2f (a )＝2，∴f (a )＝4. ∴a 2－a ＋b ＝4. ∴b ＝4－a 2＋a ＝2. 故f (x )＝x 2－x ＋2.从而f (lo g 2x )＝(log 2x )2－log 2x ＋2＝⎝⎛⎭⎪⎫log 2x －122＋74. ∴当log 2x ＝12，即x ＝2时，f (log 2x )有最小值74.(2)由题意，⎩⎪⎨⎪⎧2x2－log 2x ＋2＞2，log 2x 2－x ＋＜2⇒⎩⎪⎨⎪⎧x ＞2，或0＜x ＜1，－1＜x ＜2⇒0＜x ＜1.11．已知f (x )＝lg(a x－b x)(a ＞1＞b ＞0)． (1)求f (x )的定义域；(2)问是否存在实数a 、b ，当x ∈(1，＋∞)时，f (x )的值域为(0，＋∞)，且f (2)＝lg2？若存在，求出a 、b 的值，若不存在，说明理由．解析：(1)由a x －b x＞0及a ＞1＞b ＞0，得⎝ ⎛⎭⎪⎫a b x＞1，故x ＞0.所以，f (x )的定义域为(0，＋∞)．(2)令g (x )＝a x －b x，由a ＞1＞b ＞0知，g (x )在(0，＋∞)上为增函数． 当x ∈(1，＋∞)时，f (x )取到一切正数等价于x ∈(1，＋∞)时，g (x )＞1. 故g (1)＝1，得a －b ＝1.① 又f (2)＝lg2，故a 2－b 2＝2.② 由①②解得a ＝32，b ＝12.12．(2013·辽宁测试)已知函数f (x )＝log 4(4x＋1)＋kx (k ∈R )为偶函数． (1)求k 的值；(2)若方程f (x )＝log 4(a ·2x－a )有且仅有一个根，求实数a 的取值范围． 解析：(1)∵f (x )为偶函数， ∴f (－x )＝f (x )．即log 4(4－x＋1)－kx ＝log 4(4x＋1)＋kx ，∴log 44x＋14x －log 4(4x＋1)＝2kx ，∴(2k ＋1)x ＝0，∴k ＝－12.(2)依题意知：log 4(4x ＋1)－12x ＝log 4(a ·2x－a )．(*)∴⎩⎪⎨⎪⎧4x＋1＝a ·2x－a x，a ·2x－a ＞0，令t ＝2x ，则(*)变为(1－a )t 2＋at ＋1＝0只需其有一正根． ①a ＝1，t ＝－1不合题意；②(*)式有一正一负根，∴⎩⎪⎨⎪⎧Δ＝a 2－－a ＞0，t 1t 2＝11－a ＜0，经验证满足a ·2x－a ＞0，∴a＞1.③(*)式有两相等的根，Δ＝0，∴a ＝±22－2，又a ·2x－a ＞0，∴a ＝－2－22， 综上所述可知a 的取值范围为{a |a ＞1或a ＝－2－22}．。

2014届高三数学一轮复习专讲专练（教材回扣+考点分类+课堂内外+限时训练）：4.4 函数y＝Asin(ωx＋φ)的图像及应用一、选择题1．(2012·浙江)把函数y＝cos2x＋1的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)，然后向左平移1个单位长度，再向下平移1个单位长度，得到的图像是( )A.B.C.D.解析：把函数y ＝cos2x ＋1的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)，可得函数y ＝cos2⎝ ⎛⎭⎪⎫12x ＋1＝cos x ＋1的图像；然后向左平移1个单位长度得到函数y ＝cos(x ＋1)＋1的图像；再向下平移1个单位长度得到函数y ＝cos(x ＋1)＋1－1＝cos(x ＋1)的图像；结合各选项中的图像可知其图像为选项A 中的图像，故应选A.答案：A2．(2013·信阳调研)先将函数f (x )＝2sin ⎝ ⎛⎭⎪⎫2x －π6的周期变为原来的2倍，再将所得函数的图像向右平移π6个单位，则所得函数图像的解析式为( )A ．f (x )＝2sin xB ．f (x )＝2sin ⎝⎛⎭⎪⎫x －π3C ．f (x )＝2sin4xD ．f (x )＝2sin ⎝⎛⎭⎪⎫4x －π3 解析：f (x )＝2sin ⎝ ⎛⎭⎪⎫2x －π6的周期变为原来的2倍，得到f (x )＝2sin ⎝ ⎛⎭⎪⎫x －π6，再向右平移π6个单位，得到f (x )＝2sin ⎝⎛⎭⎪⎫x －π3.答案：B3．(2013·潍坊三县检测)已知简谐振动f (x )＝A sin(ωx ＋φ)⎝⎛⎭⎪⎫|φ|＜π2的振幅为32，图像上相邻最高点与最低点之间的距离为5，且过点⎝ ⎛⎭⎪⎫0，34，则该简谐振动的频率与初相分别为( )A.16，π6B.18，π6C.π4，π6D.16，π3解析：由题意知A ＝32，∵图像上相邻最高点与最低点之间的距离为5，∴⎝ ⎛⎭⎪⎫T 22＋32＝5，解得T ＝8，∴f ＝18，ω＝π4，由图像过点⎝ ⎛⎭⎪⎫0，34且|φ|＜π2，得φ＝π6，故选B. 答案：B4．(2013·蚌埠质检)以下关于函数f (x )＝sin2x －cos2x 的命题，正确的是( )A ．函数f (x )在区间⎝ ⎛⎭⎪⎫0，23π上单调递增B ．直线x ＝π8是函数y ＝f (x )图像的一条对称轴C ．点⎝ ⎛⎭⎪⎫π4，0是函数y ＝f (x )图像的一个对称中心 D ．将函数y ＝f (x )的图像向左平移π8个单位，可得到y ＝2sin2x 的图像解析：f (x )＝sin2x －cos2x ＝2sin ⎝ ⎛⎭⎪⎫2x －π4，将f (x )的图像向左平移π8个单位为y ＝2sin2x ，故选D. 答案：D5．(2013·眉山诊断)若把函数y ＝2cos ⎝ ⎛⎭⎪⎫x ＋π3＋1的图像向右平移m (m ＞0)个单位长度，使点⎝ ⎛⎭⎪⎫π3，1为其对称中心，则m 的最小值是( )A.π2 B.π6 C.π3D ．π 解析：y ＝2cos ⎝ ⎛⎭⎪⎫x ＋π3＋1的图像向右平移m (m ＞0)个单位长度得到y ＝2cos ⎝ ⎛⎭⎪⎫x ＋π3－m ＋1，∵⎝ ⎛⎭⎪⎫π3，1为其对称中心，∴π3＋π3－m ＝k π＋π2，k ∈Z ，∴m 的最小值是π6.答案：B6．(2013·西工大附中训练)如图所示，为了得到g (x )＝sin2x 的图像，则只需将f (x )的图像( )A ．向右平移π6个长度单位B ．向右平移π3个长度单位C ．向左平移π6个长度单位D ．向左平移π3个长度单位解析：由图像可知A ＝1，又T 4＝7π12－π3＝π4，∴T ＝π，从而ω＝2πT ＝2，将⎝ ⎛⎭⎪⎫7π12，－1代入f (x )＝sin(2x ＋φ)中，得sin ⎝⎛⎭⎪⎫7π6＋φ＝－1，又|φ|＜π2，得φ＝π3，∴f (x )＝sin ⎝⎛⎭⎪⎫2x ＋π3.将f (x )图像右移π6个长度单位即可得到g (x )＝sin2x 的图像．答案：A 二、填空题7．若将函数y ＝2sin(3x ＋φ)的图像向右平移π4个单位后得到的图像关于点⎝ ⎛⎭⎪⎫π3，0对称，则|φ|的最小值是______．解析：将函数y ＝2sin(3x ＋φ)的图像向右平移π4个单位后得到2sin ⎣⎢⎡⎦⎥⎤3⎝ ⎛⎭⎪⎫x －π4＋φ＝2sin ⎝ ⎛⎭⎪⎫3x －3π4＋φ的图像．因为该函数的图像关于点⎝⎛⎭⎪⎫π3，0对称，所以2sin ⎝ ⎛⎭⎪⎫3×π3－3π4＋φ＝2sin ⎝ ⎛⎭⎪⎫π4＋φ＝0，故有π4＋φ＝k π(k ∈Z )．解得φ＝k π－π4(k ∈Z )．当k ＝0时，|φ|取得最小值π4.答案：π48．(2013·广东六校联考)已知函数f (x )＝A sin(ωx ＋φ)(A ＞0，ω＞0,0＜φ＜π)在x ＝π6取得最大值2，且函数f (x )的最小正周期为2π.现将函数y ＝f (x )图像上各点的横坐标缩小为原来的12，纵坐标不变，再把函数图像向右平移π3个单位，得到函数y ＝g (x )的图像，则g (x )＝__________.解析：由函数f (x )的最小正周期为2π且ω＞0，可得2π＝2πω，∴ω＝1.又函数f (x )＝A sin(ωx ＋φ)(A ＞0，ω＞0,0＜φ＜π)在x ＝π6取得最大值2，则A ＝2，且sin ⎝ ⎛⎭⎪⎫π6＋φ＝1，∴π6＋φ＝π2＋2k π，k ∈Z ，∴φ＝π3＋2k π，k ∈Z ， ∴φ＝π3.故f (x )＝2sin ⎝⎛⎭⎪⎫x ＋π3.将函数y ＝f (x )图像上各点的横坐标缩小为原来的12，纵坐标不变，得到函数的解析式为y ＝2sin ⎝ ⎛⎭⎪⎫2x ＋π3，又把函数y ＝2sin ⎝ ⎛⎭⎪⎫2x ＋π3的图像向右平移π3个单位，得到g (x )＝2sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x －π3＋π3，∴g (x )＝2sin ⎝ ⎛⎭⎪⎫2x －π3. 答案：2sin ⎝⎛⎭⎪⎫2x －π39．(2013·合肥八中质检)将函数f (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π4的图像向右平移φ(φ＞0)个单位，再将图像上每一点的横坐标缩短到原来的12倍，所得图像关于直线x ＝π4对称，则φ的最小正值为________．解析：函数f (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π4的图像向右平移φ(φ＞0)个单位后变为f (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π4－2φ，再将图像上每一点的横坐标缩短到原来的12倍后，得到f (x )＝2sin ⎝ ⎛⎭⎪⎫4x ＋π4－2φ，其图像关于直线x ＝π4对称，则4×π4＋π4－2φ＝k π＋π2(k ∈Z )，∴φ＝3π8－k π2(k ∈Z )，当k ＝0时，φ的最小正值为38π. 答案：38π三、解答题10．(2013·邹城二中期中)已知函数f (x )＝2cos x ·cos ⎝⎛⎭⎪⎫x －π6－3sin 2x ＋sin x cos x .(1)求f (x )的最小正周期；(2)把f (x )的图像向右平移m 个单位后，在⎣⎢⎡⎦⎥⎤0，π2上是增函数，当|m |最小时，求m 的值．解析：(1)f (x )＝2cos x cos ⎝⎛⎭⎪⎫x －π6－3sin 2x ＋sin x cos x＝2cos x ⎝ ⎛⎭⎪⎫cos x cos π6＋sin x sin π6－3sin 2x ＋sin x cos x＝3cos 2x ＋sin x cos x －3sin 2x ＋sin x cos x ＝3(cos 2x －sin 2x )＋2sin x cos x ＝3cos2x ＋sin2x ＝2sin ⎝ ⎛⎭⎪⎫2x ＋π3.∴T ＝2π2＝π.(2)令f (x )的图像向右平移m 个单位后的函数为g (x )，则g (x )＝2sin ⎝ ⎛⎭⎪⎫2x －2m ＋π3，令－π2＋2k π≤2x －2m ＋π3≤π2＋2k π(k ∈Z )，解得－5π12＋m ＋k π≤x ≤π12＋m ＋k π，k ∈Z . ∴单调递增区间为⎣⎢⎡⎦⎥⎤－5π12＋m ＋k π，π12＋m ＋k π，k ∈Z ，周期为π，则－5π12＋m ＋k π＝0，∴m ＝5π12－k π，k ∈Z ，当|m |最小时，m ＝5π12.11．(2012·山东)已知向量m ＝(sin x,1)，n ＝⎝ ⎛⎭⎪⎫3A cos x ，A2cos2x (A ＞0)，函数f (x )＝m·n 的最大值为6.(1)求A ；(2)将函数y ＝f (x )的图像向左平移π12个单位，再将所得图像上各点的横坐标缩短为原来的12倍，纵坐标不变，得到函数y ＝g (x )的图像．求g (x )在⎣⎢⎡⎦⎥⎤0，5π24上的值域．解析：(1)f (x )＝m·n ＝3A sin x cos x ＋A2cos2x＝A ⎝⎛⎭⎪⎫32sin2x ＋12cos2x＝A sin ⎝⎛⎭⎪⎫2x ＋π6.因为A ＞0，由题意知A ＝6. (2)由(1)知f (x )＝6sin ⎝⎛⎭⎪⎫2x ＋π6. 将函数y ＝f (x )的图像向左平移π12个单位后得到y ＝6sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x ＋π12＋π6＝6sin ⎝ ⎛⎭⎪⎫2x ＋π3的图像；再将得到的图像上各点横坐标缩短为原来的12，纵坐标不变，得到y ＝6sin ⎝ ⎛⎭⎪⎫4x ＋π3的图像．因此g (x )＝6sin ⎝⎛⎭⎪⎫4x ＋π3.因为x ∈⎣⎢⎡⎦⎥⎤0，5π24，所以4x ＋π3∈⎣⎢⎡⎦⎥⎤π3，7π6.故g (x )在⎣⎢⎡⎦⎥⎤0，5π24上的值域为[－3,6]．12．(2013·西安调研)已知平面向量a ＝(cos θ，sin θ)，b ＝(cos x ，sin x )，c ＝(sin θ，－cos θ)，其中0＜θ＜π，且函数f (x )＝(a·b )cos x ＋(b·c )sin x 的图像过点⎝ ⎛⎭⎪⎫π6，1.(1)求θ的值；(2)将函数y ＝f (x )图像上各点的横坐标变为原来的2倍，纵坐标不变，得到函数y ＝g (x )的图像，求函数y ＝g (x )在⎣⎢⎡⎦⎥⎤0，π2上的最大值和最小值．解析：(1)a·b ＝cos θcos x ＋sin θsin x ＝cos(θ－x )，b·c ＝cos x sin θ－sin x cos θ＝sin(θ－x )，∴f (x )＝(a·b )cos x ＋(b·c )sin x ＝cos(θ－x )cos x ＋sin(θ－x )sin x ＝cos(θ－x －x ) ＝cos(2x －θ)，∴f ⎝ ⎛⎭⎪⎫π6＝cos ⎝ ⎛⎭⎪⎫π3－θ＝1，而0＜θ＜π，∴θ＝π3.(2)由(1)得，f (x )＝cos ⎝⎛⎭⎪⎫2x －π3，∴g (x )＝cos ⎝ ⎛⎭⎪⎫2×12x －π3，即g (x )＝cos ⎝⎛⎭⎪⎫x －π3.当x ∈⎣⎢⎡⎦⎥⎤0，π2时，－π3≤x －π3≤π6，∴12≤cos ⎝⎛⎭⎪⎫x －π3≤1， ∴当x ＝0时，g (x )取得最小值12，当x ＝π3时，g (x )取得最大值1.。

2014届高三数学一轮复习专讲专练（教材回扣+考点分类+课堂内外+限时训练）：9.4 直线与圆、圆与圆的位置关系一、选择题1．(2012·重庆)对任意的实数k ，直线y ＝kx ＋1与圆x 2＋y 2＝2的位置关系一定是( )A ．相离B ．相切C ．相交但直线不过圆心D ．相交且直线过圆心解析：圆心C (0,0)到直线kx －y ＋1＝0的距离d ＝11＋k2≤1＜ 2.∴直线与圆相交，故选C.圆与直线的位置关系一般运用圆心到直线的距离d 与半径关系判断．若直线过定点，也可通过该点在圆内、圆外或圆上去判断．答案：C2．(2012·天津)设m ，n ∈R ，若直线(m ＋1)x ＋(n ＋1)y －2＝0与圆(x －1)2＋(y －1)2＝1相切，则m ＋n 的取值范围是( )A ．[1－3，1＋3]B ．(－∞，1－3]∪[1＋3，＋∞)C ．[2－22，2＋22]D ．(－∞，2－22]∪[2＋22，＋∞) 解析：由题得|m ＋n |m ＋12＋n ＋12＝1，即(m ＋n )2＝(m ＋1)2＋(n ＋1)2≥m ＋n ＋222，令t ＝m ＋n ，得t 2－4t －4≥0，解得t ≥2＋22或t ≤2－22，故m ＋n 的取值范围为(－∞，2－22]∪[2＋22，＋∞)．答案：D3．(2013·临沂质检)已知直线x ＋y ＝a 与圆x 2＋y 2＝4交于A 、B 两点，且|O A →＋O B →|＝|O A →－O B →|，其中O 为坐标原点，则实数a 的值为( )A ．2B ．±2C ．－2D ．± 2解析：如图，作平行四边形OADB ， 则O A →＋O B →＝O D →，O A →－O B →＝B A →， ∴|O D →|＝|B A →|. 又|O A →|＝|O B →|， ∴四边形OADB 为正方形．易知|O A →|为直线在y 轴上的截距的绝对值，∴a ＝±2. 答案：B4．(2013·安徽师大附中月考)直线l ：y ＝k (x －2)＋2与圆C ：x 2＋y 2－2x －2y ＝0相切，则直线l 的一个方向向量v ＝( )A ．(2，－2)B ．(1,1)C ．(－3,2)D.⎝ ⎛⎭⎪⎫1，12 解析：由已知得(x －1)2＋(y －1)2＝2，圆心(1,1)，半径2， 直线kx －y －2k ＋2＝0. ∵直线与圆相切，∴|1－k |1＋k2＝ 2.∴k ＝－1.∴直线的一个方向向量为(2，－2). 答案：A5．(2013·珠海调研)已知点P (x ，y )是直线kx ＋y ＋4＝0(k ＞0)上一动点，PA 、PB 是圆C ：x 2＋y 2－2y ＝0的两条切线，A 、B 是切点，若四边形PACB 的最小面积是2，则k 的值为( )A. 2B.212C ．2 2D ．2 解析：圆C 的标准方程为x 2＋(y －1)2＝1，圆心C (0,1)，半径为1，∴|PC |2＝|PA |2＋1.又S 四边形PACB ＝2×12×|PA |×1＝|PA |，∴当|PA |最小时，面积最小，而此时|PC |最小． 又|PC |最小为C 到直线kx ＋y ＋4＝0的距离d ＝5k 2＋1，∴面积最小为2时，有22＝⎝ ⎛⎭⎪⎫5k 2＋12－1，解得k ＝2(k ＞0). 答案：D6．(2013·湛江调研)设O 为坐标原点，C 为圆(x －2)2＋y 2＝3的圆心，且圆上的一点M (x ，y )满足O M →·C M →＝0，则y x等于( )A.33B.33或－33C. 3D.3或－ 3解析：∵O M →·C M →＝0，∴OM ⊥CM ，∴OM 是圆的切线． 设OM 的方程为y ＝kx ， 由|2k |k 2＋1＝3，得k ＝±3，即yx ＝± 3.答案：D 二、填空题7．过点P (3,4)作圆x 2＋y 2＝1的两条切线，切点分别为A 、B ，则线段AB 的长为__________．解析：如图所示，|OP |＝32＋42＝5，|OB |＝1，则|PB |＝52－12＝26，从而|BC |＝|OB |·|PB ||OP |＝265，|AB |＝2|BC |＝465.答案：4658．已知AC 、BD 为圆O ：x 2＋y 2＝4的两条相互垂直的弦，垂足为M (1，2)，则四边形ABCD 的面积的最大值为__________．解析：设圆心O 到AC 、BD 的距离为d 1、d 2，垂足分别为E 、F ，则四边形OEMF 为矩形，则有d 21＋d 22＝3.由平面几何知识知|AC |＝24－d 21，|BD |＝24－d 22， ∴S 四边形ABCD ＝12|AC |·|BD |＝24－d 21·4－d 22 ≤(4－d 21)＋(4－d 22) ＝8－(d 21＋d 22) ＝5，即四边形ABCD 的面积的最大值为5. 答案：59．(2013·安徽联考)若直线2ax －by ＋2＝0(a ＞0，b ＞0)被圆x 2＋y 2＋2x －4y ＋1＝0截得的弦长为4，则ab 的最大值是__________．解析：圆x 2＋y 2＋2x －4y ＋1＝0的圆心为(－1,2)，半径r ＝2， 若直线截得的弦长为4，则圆心在直线上， 所以－2a －2b ＋2＝0，即a ＋b ＝1. 所以ab ≤⎝⎛⎭⎪⎫a ＋b 22＝14，当且仅当a ＝b ＝12时取等号．故(ab )max ＝14.答案：14三、解答题10．在平面直角坐标系xOy 中，曲线y ＝x 2－6x ＋1与坐标轴的交点都在圆C 上． (1)求圆C 的方程；(2)若圆C 与直线x －y ＋a ＝0交于A ，B 两点，且OA ⊥OB ，求a 的值．解析：(1)曲线y ＝x 2－6x ＋1与y 轴的交点为(0,1)，与x 轴的交点为(3＋22，0)，(3－22，0)．故可设C 的圆心为(3，t )，则有32＋(t －1)2＝(22)2＋t 2，解得t ＝1.则圆C 的半径为32＋t －12＝3.所以圆C 的方程为(x －3)2＋(y －1)2＝9.(2)设A (x 1，y 1)，B (x 2，y 2)，其坐标满足方程组：⎩⎪⎨⎪⎧x －y ＋a ＝0，x －32＋y －12＝9.消去y ，得到方程2x 2＋(2a －8)x ＋a 2－2a ＋1＝0. 由已知可得，判别式Δ＝56－16a －4a 2＞0. 因此x 1,2＝8－2a ±56－16a －4a 24，从而x 1＋x 2＝4－a ，x 1x 2＝a 2－2a ＋12.①由于OA ⊥OB ，可得x 1x 2＋y 1y 2＝0. 又y 1＝x 1＋a ，y 2＝x 2＋a ， 所以2x 1x 2＋a (x 1＋x 2)＋a 2＝0.②由①，②得a ＝－1，满足Δ＞0，故a ＝－1.11．(2013·苏北三市联考)已知平面区域⎩⎪⎨⎪⎧x ≥0，y ≥0，x ＋2y －4≤0恰好被面积最小的圆C ：(x －a )2＋(y －b )2＝r 2及其内部所覆盖．(1)试求圆C 的方程；(2)若斜率为1的直线l 与圆C 交于不同两点A 、B ，满足CA ⊥CB ，求直线l 的方程． 解析：(1)由题意知此平面区域表示的是以O (0,0)，P (4,0)，Q (0,2)构成的三角形及其内部，且△OPQ 是直角三角形，所以覆盖它的且面积最小的圆是其外接圆，故圆心是(2,1)，半径是5，所以圆C 的方程是(x －2)2＋(y －1)2＝5. (2)设直线l 的方程是y ＝x ＋b ， 因为CA ⊥CB ，所以圆C 到直线l 的距离是102， 即|2－1＋b |12＋12＝102，解得b ＝－1± 5. 所以直线l 的方程为y ＝x －1± 5.12．(2013·揭阳调研)已知点M (3,1)，直线ax －y ＋4＝0及圆(x －1)2＋(y －2)2＝4. (1)求过M 点的圆的切线方程；(2)若直线ax －y ＋4＝0与圆相切，求a 的值；(3)若直线ax －y ＋4＝0与圆相交于A 、B 两点，且弦AB 的长为23，求a 的值． 解析：(1)圆心C (1,2)，半径为r ＝2， 当直线的斜率不存在时，方程为x ＝3.由圆心C (1,2)到直线x ＝3的距离d ＝3－1＝2＝r 知， 此时，直线与圆相切．当直线的斜率存在时，设方程为y －1＝k (x －3)， 即kx －y ＋1－3k ＝0.由题意知|k －2＋1－3k |k 2＋1＝2，解得k ＝34.∴方程为y －1＝34(x －3)，即3x －4y －5＝0.故过M 点的圆的切线方程为x ＝3或3x －4y －5＝0. (2)由题意有|a －2＋4|a 2＋1＝2，解得a ＝0或a ＝43.(3)∵圆心到直线ax －y ＋4＝0的距离为|a ＋2|a 2＋1，∴⎝⎛⎭⎪⎫|a ＋2|a 2＋12＋⎝ ⎛⎭⎪⎫2322＝4，解得a ＝－34.。