2014届高三数学一轮复习导学案：抛物线

第七讲 抛物线知识梳理·双基自测知识梳理知识点一 抛物线的定义 抛物线需要满足以下三个条件： (1)在平面内；(2)动点到定点F 的距离与到定直线l 的距离__相等__； (3)定点F 与定直线l 的关系为__点F ∉l __． 知识点二 抛物线的标准方程与几何性质 标准 方程y 2＝2px (p ＞0)y 2＝－2px (p ＞0)x 2＝2py (p ＞0)x 2＝－2py (p ＞0)p 的几何意义：焦点F 到准线l 的距离图形顶点 O (0,0)对称轴 y ＝0x ＝0焦点 F __⎝⎛⎭⎫p 2，0__F __⎝⎛⎭⎫－p2，0__ F __⎝⎛⎭⎫0，p2__ F __⎝⎛⎭⎫0，－p2__ 离心率 e ＝__1__准线方程 __x ＝－p2____x ＝p2____y ＝－p2____y ＝p 2__范围 x ≥0，y ∈Rx ≤0，y ∈Ry ≥0，x ∈Ry ≤0，x ∈R开口方向 向右 向左 向上 向下 焦半径 (其中P (x 0，y 0))|PF |＝ __x 0＋p 2__|PF |＝ __－x 0＋p2__|PF |＝ __y 0＋p 2__|PF |＝ __－y 0＋p2__归纳拓展抛物线焦点弦的处理规律直线AB 过抛物线y 2＝2px (p ＞0)的焦点F ，交抛物线于A (x 1，y 1)，B (x 2，y 2)两点，如图．(1)y 1y 2＝－p 2，x 1x 2＝p 24． (2)|AB |＝x 1＋x 2＋p ，x 1＋x 2≥2x 1x 2＝p ，即当x 1＝x 2时，弦长最短为2p ． (3)1|AF |＋1|BF |＝2p． (4)弦长AB ＝2psin 2α(α为AB 的倾斜角)．(5)以AB 为直径的圆与准线相切．(6)焦点F 对A ，B 在准线上射影的张角为90°． (7)A 、O 、D 三点共线；B 、O 、C 三点共线．双基自测题组一 走出误区1．判断下列结论是否正确(请在括号中打“√”或“×”)(1)平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹一定是抛物线．( × ) (2)方程y ＝ax 2(a ≠0)表示的曲线是焦点在x 轴上的抛物线，且其焦点坐标是⎝⎛⎭⎫a 4，0，准线方程是x ＝－a4．( × )(3)抛物线既是中心对称图形，又是轴对称图形．( × ) (4)AB 为抛物线y 2＝2px (p ＞0)的过焦点F ⎝⎛⎭⎫p 2，0的弦，若A (x 1，y 1)，B (x 2，y 2)，则x 1x 2＝p 24，y 1y 2＝－p 2，弦长|AB |＝x 1＋x 2＋p ．( √ )(5)过抛物线的焦点与抛物线对称轴垂直的直线被抛物线截得的线段叫做抛物线的通径，那么抛物线x 2＝－2ay (a ＞0)的通径长为2a ．( √ )题组二 走进教材2．(必修2P 69例4)(2021·甘肃张掖诊断)过抛物线y 2＝4x 的焦点的直线l 交抛物线于P (x 1，y 1)，Q (x 2，y 2)两点，如果x 1＋x 2＝6，则|PQ |等于( B )A ．9B ．8C ．7D ．6[解析] 抛物线y 2＝4x 的焦点为F (1,0)，准线方程为x ＝－1．根据题意可得，|PQ |＝|PF |＋|QF |＝x 1＋1＋x 2＋1＝x 1＋x 2＋2＝8．3．(2021·河南郑州名校调研)抛物线y ＝－4x 2上的一点M 到焦点的距离为1，则点M 的纵坐标是( B )A ．－1716B ．－1516C ．716D ．1516[解析] 由抛物线的方程y ＝－4x 2，可得标准方程为x 2＝－14y ，则焦点坐标为F ⎝⎛⎭⎫0，－116，准线方程为y ＝116，设M (x 0，y 0)，则由抛物线的定义可得－y 0＋116＝1，解得y 0＝－1516．故选B ．题组三 走向高考4．(2019·课标全国Ⅱ)若抛物线y 2＝2px (p ＞0)的焦点是椭圆x 23p ＋y 2p＝1的一个焦点，则p＝( D )A ．2B ．3C ．4D ．8[解析] ∵抛物线y 2＝2px (p ＞0)的焦点坐标为⎝⎛⎭⎫p 2，0， ∴椭圆x 23p ＋y 2p ＝1的一个焦点为⎝⎛⎭⎫p 2，0， ∴3p －p ＝p 24，∴p ＝8．故选D ．5．(2020·新课标Ⅰ)已知A 为抛物线C ：y 2＝2px (p ＞0)上一点，点A 到C 的焦点的距离为12，到y 轴的距离为9，则p ＝( C )A ．2B ．3C ．6D ．9[解析] A 为抛物线C ：y 2＝2px (p ＞0)上一点，点A 到C 的焦点的距离为12，到y 轴的距离为9，因为抛物线上的点到焦点的距离和到准线的距离相等，故有：9＋p2＝12⇒p ＝6；故选C ．考点突破·互动探究考点一 抛物线的定义及应用——多维探究 角度1 轨迹问题例1 (1)动圆与定圆A ：(x ＋2)2＋y 2＝1外切，且和直线x ＝1相切，则动圆圆心的轨迹是(D)A．直线B．椭圆C．双曲线D．抛物线[解析]设动圆的圆心为C，则C到定圆A：(x＋2)2＋y2＝1的圆心的距离等于r＋1，而动圆的圆心到直线x＝1的距离等于r，所以动圆到直线x＝2距离为r＋1，即动圆圆心到定点(－2,0)和定直线x＝2的距离相等，根据抛物线的定义知，动圆的圆心轨迹为抛物线，所以答案为D．角度2到焦点与到定点距离之和最小问题(2)①(2021·河北保定七校联考)已知M是抛物线x2＝4y上一点，F为其焦点，C为圆(x ＋1)2＋(y－2)2＝1的圆心，则|MF|＋|MC|的最小值为(B)A．2 B．3C．4 D．5②(2021·山西运城联考)已知抛物线C：x2＝8y的焦点为F，O为原点，点P是抛物线C 的准线上的一动点，点A在抛物线C上，且|AF|＝4，则|P A|＋|PO|的最小值为(B) A．4 2 B．213C．313 D．4 6[解析]①设抛物线x2＝4y的准线方程为l：y＝－1，C为圆(x＋1)2＋(y－2)2＝1的圆心，所以C的坐标为(－1,2)，过M作l的垂线，垂足为E，根据抛物线的定义可知|MF|＝|ME|，所以问题求|MF|＋|MC|的最小值，就转化为求|ME|＋|MC|的最小值，由平面几何的知识可知，当C，M，E在一条直线上时，此时CE⊥l，|ME|＋|MC|有最小值，最小值为|CE|＝2－(－1)＝3，故选B．②由抛物线的定义知|AF|＝y A＋p2＝y A＋2＝4，∴y A＝2，代入x2＝8y，得x A＝±4，不妨取A(4,2)，又O关于准线y＝－2的对称点为O′(0，－4)，∴|P A|＋|PO|＝|P A|＋|PO′|≥|AO′|＝(－4－2)2＋(0－4)2＝213，当且仅当A、P、O′共线时取等号，故选B．[引申]本例(2)①中，(ⅰ)|MC |－|MF |的最大值为__2__；最小值为__－2__；(ⅱ)若N 为⊙C 上任一点，则|MF |＋|MN |的最小值为__2__．角度3 到准线与到定点距离之和最小问题(3)已知圆C ：x 2＋y 2＋6x ＋8y ＋21＝0，抛物线y 2＝8x 的准线为l ，设抛物线上任意一点P 到直线l 的距离为d ，则d ＋|PC |的最小值为( A )A ．41B ．7C ．6D ．9[解析] 由题意得圆的方程为(x ＋3)2＋(y ＋4)2＝4，圆心C 的坐标为(－3，－4)．由抛物线定义知，当d ＋|PC |最小时为圆心与抛物线焦点间的距离，即d ＋|PC |＝(－3－2)2＋(－4)2＝41．角度4 到两定直线的距离之和最小问题(4)(2021·北京人大附中测试)点P 在曲线y 2＝4x 上，过P 分别作直线x ＝－1及y ＝x ＋3的垂线，垂足分别为G ，H ，则|PG |＋|PH |的最小值为( B )A ．322B ．2 2C ．322＋1D ．2＋2[解析] 由题可知x ＝－1是抛物线的准线，焦点F (1,0)，由抛物线的性质可知|PG |＝|PF |，∴|PG |＋|PH |＝|PF |＋|PH |≤|FH |＝|1－0＋3|2＝22，当且仅当H 、P 、F 三点共线时取等号，∴|PG |＋|PH |的最小值为22．故选B ．名师点拨利用抛物线的定义可解决的常见问题(1)轨迹问题：用抛物线的定义可以确定动点与定点、定直线距离有关的轨迹是否为抛物线．(2)距离问题：涉及抛物线上的点到焦点的距离和到准线的距离问题时，注意在解题中利用两者之间的关系进行相互转化．(3)看到准线想焦点，看到焦点想准线，这是解决抛物线焦点弦有关问题的重要途径． 〔变式训练1〕(1)(角度1)到定点A (0,2)的距离比到定直线l ：y ＝－1大1的动点P 的轨迹方程为__x 2＝8y __．(2)(角度1)(2021·吉林省吉林市调研)已知抛物线y 2＝4x 的焦点F ，点A (4,3)，P 为抛物线上一点，且P 不在直线AF 上，则△P AF 周长取最小值时，线段PF 的长为( B )A ．1B ．134C ．5D ．214(3)(角度2)(2021·山西大学附中模拟)已知点Q (22，0)及抛物线y ＝x 24上一动点P (x ，y )，则y ＋|PQ |的最小值是__2__．(4)(角度3)(2021·上海虹口区二模)已知直线l 1：4x －3y ＋6＝0和直线l 2：x ＝－1，抛物线y 2＝4x 上一动点P 到直线l 1和l 2的距离之和的最小值为( C )A ．3716B ．115C ．2D ．74[解析] (1)由题意知P 到A 的距离等于其到直线y ＝－2的距离，故P 的轨迹是以A 为焦点，直线y ＝－2为准线的抛物线，所以其方程为x 2＝8y ．(2)求△P AF 周长的最小值，即求|P A |＋|PF |的最小值，设点P 在准线上的射影为D ，根据抛物线的定义，可知|PF |＝|PD |，因此，|P A |＋|PF |的最小值，即|P A |＋|PD |的最小值．根据平面几何知识，可得当D ，P ，A 三点共线时|P A |＋|PD |最小，此时P ⎝⎛⎭⎫94，3，且|PF |＝94＋1＝134，故选B ．(3)抛物线y ＝x 24即x 2＝4y ，其焦点坐标为F (0,1)，准线方程为y ＝－1．因为点Q 的坐标为(22，0)，所以|FQ |＝(22)2＋12＝3．过点P 作准线的垂线PH ，交x 轴于点D ，如图所示．结合抛物线的定义，有y ＋|PQ |＝|PD |＋|PQ |＝|PH |＋|PQ |－1＝|PF |＋|PQ |－1≥|FQ |－1＝3－1＝2，即y ＋|PQ |的最小值是2．(4)直线l 2：x ＝－1是抛物线y 2＝4x 的准线，抛物线y 2＝4x 的焦点为F (1,0)，则点P 到直线l 2：x ＝－1的距离等于PF ，过点F 作直线l 1：4x －3y ＋6＝0的垂线，和抛物线的交点就是点P ，所以点P 到直线l 1：4x －3y ＋6＝0的距离和到直线l 2：x ＝－1的距离之和的最小值就是点F (1,0)到直线l 1：4x －3y ＋6＝0的距离，所以最小值为|4－0＋6|32＋42＝2，故选C ．考点二 抛物线的标准方程——自主练透例2 (1)过点P (－3,2)的抛物线的标准方程为__y 2＝－43x 或x 2＝92y __．(2)焦点在直线x －2y －4＝0上的抛物线的标准方程为__y 2＝16x 或x 2＝－8y __，准线方程为__x ＝－4或y ＝2__．(3)如图，过抛物线y 2＝2px (p ＞0)的焦点F 的直线依次交抛物线及准线于点A ，B ，C ，若|BC |＝2|BF |，且|AF |＝3，则抛物线的方程为( B )A ．y 2＝32xB ．y 2＝3xC ．y 2＝92xD ．y 2＝9x[解析] (1)设所求抛物线的方程为y 2＝－2px (p ＞0)或x 2＝2py (p ＞0)． ∵过点(－3,2)，∴4＝－2p ·(－3)或9＝2p ·2． ∴p ＝23或p ＝94．∴所求抛物线的标准方程为y 2＝－43x 或x 2＝92y ．(2)令x ＝0，得y ＝－2，令y ＝0，得x ＝4． ∴抛物线的焦点为(4,0)或(0，－2)． 当焦点为(4,0)时，p2＝4，∴p ＝8，此时抛物线方程为y 2＝16x ； 当焦点为(0，－2)时，p2＝2，∴p ＝4，此时抛物线方程为x 2＝－8y ．∴所求的抛物线的标准方程为y 2＝16x 或x 2＝－8y ， 对应的准线方程分别是x ＝－4，y ＝2．(3)如图，分别过点A ，B 作准线的垂线，分别交准线于点E ，D ，设|BF |＝a ，则由已知得|BC |＝2a ，由定义得|BD |＝a ，故∠BCD ＝30°． 在直角三角形ACE 中，∵|AE |＝|AF |＝3，|AC |＝3＋3a ，2|AE |＝|AC |， ∴3＋3a ＝6，从而得a ＝1．∵BD ∥FG ，∴|BD ||FG |＝|BC ||FC |，即1p ＝23，求得p ＝32，因此抛物线的方程为y 2＝3x ．名师点拨求抛物线的标准方程的方法(1)求抛物线的标准方程常用待定系数法，若焦点位置确定，因为未知数只有p ，所以只需一个条件确定p 值即可．(2)因为抛物线方程有四种标准形式，因此求抛物线方程时，需先定位，再定量．一般焦点在x 轴上的抛物线的方程可设为y 2＝ax (a ≠0)；焦点在y 轴上的抛物线的方程可设为x 2＝ay (a ≠0)．〔变式训练2〕(1)(2021·重庆沙坪坝区模拟)已知抛物线C ：y 2＝2px (p ＞0)的焦点为F ，过点(p,0)且垂直于x 轴的直线与抛物线C 在第一象限内的交点为A ，若|AF |＝1，则抛物线C 的方程为( A )A ．y 2＝43xB ．y 2＝2xC ．y 2＝3xD ．y 2＝4x(2)(2021·安徽蚌埠一中期中)已知抛物线的顶点在原点，焦点在y 轴上，其上的点P (m ，－3)到焦点的距离为5，则抛物线方程为( D )A ．x 2＝8yB ．x 2＝4yC ．x 2＝－4yD ．x 2＝－8y[解析] (1)由题意知x A ＝p ，又|AF |＝x A ＋p 2＝3p 2＝1，∴p ＝23，∴抛物线C 的方程为y 2＝43x ，故选A ．(2)由题意可知抛物线的焦点在y 轴负半轴上，故设其方程为x 2＝－2py (p ＞0)，所以3＋p2＝5，即p ＝4，所以所求抛物线方程为x 2＝－8y ，故选D ．考点三,抛物线的几何性质——师生共研例3 (1)(2021·广西四校联考)已知抛物线y 2＝2px (p ＞0)上横坐标为4的点到此抛物线焦点的距离为9，则该抛物线的焦点到准线的距离为( C )A ．4B ．9C ．10D ．18(2)(理)(2021·四川眉山模拟)点F 为抛物线C ：y 2＝2px (p ＞0)的焦点，过F 的直线交抛物线C 于A ，B 两点(点A 在第一象限)，过A 、B 分别作抛物线C 的准线的垂线段，垂足分别为M 、N ，若|MF |＝4，|NF |＝3，则直线AB 的斜率为( D )A ．1B ．724C ．2D ．247(文)(2021·四川师大附中期中)已知抛物线y 2＝2px (p ＞0)，F 为抛物线的焦点，O 为坐标原点A (x 1，y 1)，B (x 2，y 2)为抛物线上的两点，A ，B 的中点到抛物线准线的距离为5，△ABO 的重心为F ，则p ＝( D )A ．1B ．2C ．3D ．4[解析] (1)抛物线y 2＝2px 的焦点为⎝⎛⎭⎫p 2，0，准线方程为x ＝－p 2．由题意可得4＋p2＝9，解得p ＝10，所以该抛物线的焦点到准线的距离为10．故选C ．(2)(理)由抛物线定义知|AM |＝|AF |，|BN |＝|BF |， ∴∠AFM ＋∠BFM ＝360°－∠MAF －∠NBF2＝90°，∴∠MFN ＝90°， 又|MF |＝4，|NF |＝3， ∴|MN |＝5，∴p ＝|KF |＝|MF |·|NF ||MN |＝125， 又∠AFM ＝∠AMF ＝∠MFK ，∴k AB ＝tan(180°－2∠MFK )＝－2tan ∠MFK 1－tan 2∠MFK ＝－831－⎝⎛⎭⎫432＝247．故选D ．(文)x 1＋x 22＋p 2＝5，x 1＋x 2＋03＝p 2，∴10－p ＝3p2，所以p ＝4．故选D ．名师点拨在解决与抛物线的性质有关的问题时，要注意利用几何图形形象、直观的特点来解题，特别是涉及焦点、顶点、准线的问题更是如此．〔变式训练3〕(1)(2021·广东茂名五校联考)设抛物线y 2＝2px (p ＞0)的焦点为F (1,0)，过焦点的直线交抛物线于A 、B 两点，若|AF |＝4|BF |，则|AB |＝__254__． (2)(2021·湖北荆州模拟)从抛物线y 2＝4x 在第一象限内的一点P 引抛物线准线的垂线，垂足为M ，且|PM |＝9，设抛物线的焦点为F ，则直线PF 的斜率为( C )A ．627B ．1827C ．427D ．227[解析] (1)∵p2＝1，∴p ＝2，不妨设直线AB 方程为x ＝my ＋1，A (x 1，y 1)，B (x 2，y 2)，由⎩⎪⎨⎪⎧y 2＝4x x ＝my ＋1，得y 2－4my －4＝0， ∴y 1y 2＝－4，又|AF |＝4|BF |，∴y 1＝－4y 2， ∴y 2＝－1，从而x 2＝14，∴|BF |＝1＋14＝54，∴|AB |＝5|BF |＝254． (2)设P (x 0，y 0)，由抛物线y 2＝4x ， 可知其焦点F 的坐标为(1,0)， 故|PM |＝x 0＋1＝9，解得x 0＝8，故P 点坐标为(8,42)， 所以k PF ＝0－421－8＝427．故选C ．考点四,直线与抛物线的综合问题——师生共研例4 (1)已知抛物线y 2＝2px (p ＞0)的焦点F 与双曲线x 212－y 24＝1的一个焦点重合，直线y ＝x －4与抛物线交于A ，B 两点，则|AB |等于( B )A ．28B ．32C ．20D ．40(2)(2021·陕西师大附中期中)已知抛物线y 2＝4x 的一条弦AB 恰好以P (1,1)为中点，则弦AB 所在直线的方程是( B )A ．y ＝x －1B ．y ＝2x －1C ．y ＝－x ＋2D ．y ＝－2x ＋3(3)(2021·湖南五市十校联考)已知抛物线C ：y 2＝2px (p ＞0)，直线y ＝x －1与C 相交所得的长为8．①求p 的值；②过原点O 的直线l 与抛物线C 交于M 点，与直线x ＝－1交于H 点，过点H 作y 轴的垂线交抛物线C 于N 点，求证：直线MN 过定点．[解析] (1)双曲线x 212－y 24＝1的焦点坐标为(±4,0)，故抛物线的焦点F 的坐标为(4,0)．因此p ＝8，故抛物线方程为y 2＝16x ，易知直线y ＝x －4过抛物线的焦点．设A 、B 两点坐标分别为(x 1，y 1)，(x 2，y 2)．由⎩⎪⎨⎪⎧y 2＝16x ，y ＝x －4，可得x 2－24x ＋16＝0，故x 1＋x 2＝24． 故|AB |＝x 1＋x 2＋p ＝24＋8＝32．故选B ． (2)设A (x 1，y 1)，B (x 2，y 2)，∴y 1＋y 2＝2，由⎩⎪⎨⎪⎧y 21＝4x 1y 22＝4x 2，知k AB ＝y 1－y 2x 1－x 2＝4y 1＋y 2＝2，∴AB 的方程为y －1＝2(x －1)，即2x －y －1＝0，故选B ．(3)①由⎩⎪⎨⎪⎧y 2＝2px y ＝x －1，消x 可得y 2－2py －2p ＝0，∴y 1＋y 2＝2p ，y 1y 2＝－2p ， ∴弦长为1＋12·(y 1＋y 2)2－4y 1y 2＝2·4p 2＋8p ＝8，解得p ＝2或p ＝－4(舍去)， ∴p ＝2，②由①可得y 2＝ 4x ，设M ⎝⎛⎭⎫14y 20，y 0， ∴直线OM 的方程y ＝4y 0x ，当x ＝－1时，∴y H ＝－4y 0，代入抛物线方程y 2＝4x ，可得x N ＝4y 20，∴N ⎝⎛⎭⎫4y2，－4y 0， ∴直线MN 的斜率k ＝y 0＋4y 0y 204－4y 20＝4y 0y 20－4，直线MN 的方程为y －y 0＝4y 0y 20－4⎝⎛⎭⎫x －14y 20， 整理可得y ＝4y 0y 20－4(x －1)，故直线MN 过点(1,0)．名师点拨(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要将两方程联立，消元，用到根与系数的关系．(2)有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点．若过抛物线的焦点(设焦点在x 轴的正半轴上)，可直接使用公式|AB |＝x 1＋x 2＋p ，若不过焦点，则必须用一般弦长公式．(3)涉及抛物线的弦长、中点、距离等相关问题时，一般利用根与系数的关系采用“设而不求”“整体代入”等解法．提醒：涉及弦的中点、斜率问题一般用“点差法”求解． 〔变式训练4〕(1)(2021·甘肃诊断)直线l 过抛物线y 2＝2px (p ＞0)的焦点，且交抛物线于A ，B 两点，交其准线于C 点，已知|AF |＝4，CB →＝3BF →，则p ＝( C )A ．2B ．43C ．83D ．4(2)(2021·安徽皖南八校模拟)已知抛物线C ：y 2＝2px (p ＞0)的焦点F 到直线x －y ＋1＝0的距离为2．①求抛物线C 的方程；②过点F 的直线l 与C 交于A ，B 两点，交y 轴于点P ．若|AB →|＝3|BP →|，求直线l 的方程． [解析] (1)过A ，B 分别作准线的垂线交准线于E ，D 两点， 设|BF |＝a ，根据抛物线的性质可知，|BD |＝a ， |AE |＝4，根据平行线段比例可知|BD ||AE |＝|CB ||AC |，即a 4＝3a 3a ＋a ＋4，解得a ＝2， 又|BD ||GF |＝|BC ||CF |，即a p ＝3a4a， 解得p ＝43a ＝83，故选C ．(2)①由抛物线C ：y 2＝2px (p ＞0)，可得焦点F ⎝⎛⎭⎫p 2，0， 因为焦点到x －y ＋1＝0的距离为2，即⎪⎪⎪⎪p 2＋12＝2，解得p ＝2，所以抛物线C 的方程y 2＝4x ．②由①知焦点F (1,0)，设直线l ：y ＝k (x －1)， A (x 1，y 1)，B (x 2，y 2)，联立方程组⎩⎪⎨⎪⎧y ＝k (x －1)y 2＝4x，整理得k 2x 2－(2k 2＋4)x ＋k 2＝0， 所以x 1＋x 2＝2＋4k 2，①x 1x 2＝1，②又由|AB →|＝3|BP →|，得AB →＝3BP →， 可得x 1＝4x 2，③由②③，可得x 1＝2，x 2＝12，代入①，可得2＋4k 2＝52，解得k ＝±22，所以直线l 的方程为22x － y －22＝0或22x ＋y －22＝0．名师讲坛·素养提升巧解抛物线的切线问题例5 (1)抛物线C 1：x 2＝2py (p ＞0)的焦点与双曲线C 2：x 23－y 2＝1的右焦点的连线交C 1于第一象限的点M ．若C 1在点M 处的切线平行于C 2的一条渐近线，则p ＝(D )A ．316B ．38C ．233D ．433(2)(2019·新课标Ⅲ，节选)已知曲线C ：y ＝x 22，D 为直线y ＝－12上的动点，过D 作C 的两条切线，切点分别为A ，B ．证明：直线AB 过定点．[解析] (1)抛物线C 1：x 2＝2py (p ＞0)的焦点坐标为⎝⎛⎭⎫0，p 2，双曲线x 23－y 2＝1的右焦点坐标为(2,0)，两点连线的方程为y ＝－p4(x －2)，联立⎩⎨⎧y ＝－p4(x －2)，y ＝12p x 2，得2x 2＋p 2x －2p 2＝0．设点M 的横坐标为m ，易知在M 点处切线的斜率存在，则在点M 处切线的斜率为y ′⎪⎪⎪⎪x ＝m＝⎝⎛⎭⎫12p x 2′x ＝m ＝m p． 又双曲线x 23－y 2＝1的渐近线方程为x 3±y ＝0，其与切线平行，所以m p ＝33，即m ＝33p ，代入2x 2＋p 2x －2p 2＝0，得p ＝433或p ＝0(舍去)．(2)设D ⎝⎛⎭⎫t ，－12，A (x 1，y 1)， 则x 21＝2y 1，由于y ′＝x ，∴切线DA 的斜率为x 1，故y 1＋12x 1－t ＝x 1，整理得：2tx 1－2y 1＋1＝0．设B (x 2，y 2)，同理可得2tx 2－2y 2＋1＝0． 故直线AB 的方程为2tx －2y ＋1＝0，即y －12＝tx ．∴直线AB 过定点⎝⎛⎭⎫0，12．名师点拨利用导数工具解决抛物线的切线问题，使问题变得巧妙而简单，若用判别式解决抛物线的切线问题，计算量大，易出错．注意：直线与抛物线只有一个公共点是直线与抛物线相切的必要不充分条件，过抛物线外一点与抛物线只有一个公共点的直线有0条或3条；过抛物线上一点和抛物线只有一个公共点的直线有2条．〔变式训练5〕(1)已知抛物线C ：y 2＝2px (p ＞0)，过点M ⎝⎛⎭⎫－p2，0作C 的切线，则切线的斜率为__±1__． (2)已知抛物线x 2＝8y ，过点P (b,4)作该抛物线的切线P A ，PB ，切点为A ，B ，若直线AB恒过定点，则该定点为( C )A ．(4,0)B ．(3,2)C ．(0，－4)D ．(4,1)[解析] (1)设斜率为k ，则切线为y ＝k ⎝⎛⎭⎫x ＋p 2代入y 2＝2px 中得k 2x 2＋p (k 2－2)x ＋k 2p 24＝0． Δ＝0，即p 2(k 2－2)2－4·k 2·k 2p 24＝0．解得k 2＝1，∴k ＝±1．(2)设A ，B 的坐标为(x 1，y 1)，(x 2，y 2)， ∵y ＝x 28，y ′＝x4，∴P A ，PB 的方程y －y 1＝x 14(x －x 1)，y －y 2＝x 24(x －x 2)，由y 1＝x 218，y 2＝x 228，可得y ＝x 14x －y 1，y ＝x 24x －y 2，∵切线P A ，PB 都过点P (b,4)， ∴4＝x 14×b －y 1,4＝x 24×b －y 2，故可知过A ，B 两点的直线方程为4＝b4x －y ，当x ＝0时，y ＝－4，∴直线AB 恒过定点(0，－4)．故选C ．。

抛物线一.知识回顾:(一.)抛物线的定义:平面内到一个定点F 和一条直线l 的距离相等的点的轨迹叫做抛物线，定点F 叫做抛物线的焦点，直线l 叫做抛物线的准线(二 ) 抛物线几何性质:(三).二.例题分析抛物线定义应用【例1】设圆C 与圆1)3(22=-+y x 外切，与直线y ＝0相切，则C 的圆心轨迹为( ) A ．抛物线 B ．双曲线 C ．椭圆 D ．圆变式1:设点F(2,0)，动点P 到y 轴的距离为d ，求满足条件|PF|－d ＝2的点P 的轨迹方程变式2:顶点在原点，对称轴为x 轴，抛物线上的点()3,M m -到焦点的距离等于5；【例2】已知AB 是过抛物线px y 22=(p>0)的焦点的弦,F 为抛物线的焦点, ),(),,(2211y x B y x A ,证明: （1）12||;AB x x p =++（2）以AB 为直径的圆与抛物线的准线相切。

抛物线的标准方程与性质【例3】求满足下列条件的抛物线的标准方程，并求对应抛物线的准线方程：⑴准线方程是x ＝－14； ⑵焦点在直线240x y --=上； ⑶过点P ()3,2-【例4】⑴已知抛物线的标准方程为0522=+x y ，则它的焦点坐标为________，准线方程为________⑵已知抛物线顶点在原点，焦点在x 轴上，又知抛物线上一点A (4，m )到准线距离为6，则m ＝_______. ⑶抛物线221x y -=的焦点坐标为________ 直线与抛物线的位置关系【例5】 ⑴已知正方形的一条边AB 在直线y ＝x ＋4上，顶点C 、D 在抛物线x y =2上，求该正方形的边长． ⑵已知抛物线方程为)0(22>=p px y ，直线m y x l =+:过抛物线的焦点F 且被抛物线截得的弦长为3，求p 的值与抛物线有关的最值问题【例6】⑴已知抛物线x y 22=的焦点是F ，点P 是抛物线上的动点，又有点A (3,2)，求PF PA +的最小值，并求出取最小值时点P 的坐标⑵已知抛物线x y 22=的焦点是F ，点P 是抛物线上的动点，又有点A (2,3)，求PF PA +的最小值，并求出取最小值时点P 的坐标⑶已知点P 是抛物线x y 22=上的一个动点，求点P 到点(0,2)的距离与P 到该抛物线准线的距离之和的最小值⑷已知1l :4x －3y ＋6＝0和2l :x ＝－1,求抛物线x y 42=上一动点P 到直线1l 和2l 的距离之和的最小值【习题】1. 抛物线y x 42=上一点A 的纵坐标为4，则点A 与抛物线焦点的距离为 ( ).A 2 .B 3 .C 4 .D 52. 抛物线2x y -=的点到直线0834=-+y x 距离的最小值是( ).A 43 .B 73 .C 85 .D 33. 设抛物线px y 22= (p >0)的焦点为F ，点A (0,2)，若线段FA 的中点B 在抛物线上，则B 到该抛物线准线的距离为________4. 已知过抛物线x y 42=的焦点F 的直线交该抛物线于A 、B 两点，AF ＝2，则BF ＝________ 5. 抛物线x y 42=的弦AB 垂直于x 轴，若AB 的长为34，则焦点到AB 的距离是______6. 已知椭圆191622=+y x 的右焦点为2F ，在y 轴正半轴上的顶点为2B ，求分别以2F ，2B 为焦点的抛物线标准方程及其准线方程7. 设抛物线mx y =2的准线与直线x ＝1的距离为3，求抛物线方程． 8.px y 22=(p ＞0)有一内接直角三角形,直角顶点在原点,一直角边的方程是y ＝2x ,斜边长是5,求此抛物线方程9. 顶点在原点，焦点在x 轴上的抛物线与直线y ＝2x ＋1交于P 、Q 两点，已知PQ ＝15,求抛物线的方程 10. 已知抛物线C 的顶点为坐标原点，焦点在x 轴上，直线y ＝x 与抛物线C 交于A ，B 两点．若P(2,2)为AB 的中点，求抛物线C 的方程 11. 已知△ABC 的顶点A ，B 的坐标分别为A(0,0)，B(6,0)，顶点C 在曲线32+=x y 上运动，求△ABC 重心的轨迹方程12. 抛物线x2＝4y 的焦点为F ，过点(0，－1)作直线交抛物线于不同两点A 、B ，以AF 、BF 为邻边作平行四边形FARB ，求顶点R 的轨迹方程⑸顶点在原点，对称轴为x 轴且截直线210x y -+=求抛物线的方程⑹过抛物线px y 22=的焦点F 作x 轴的垂线交抛物线于A ，B 两点，且|AB |＝6. 求抛物线的方程。

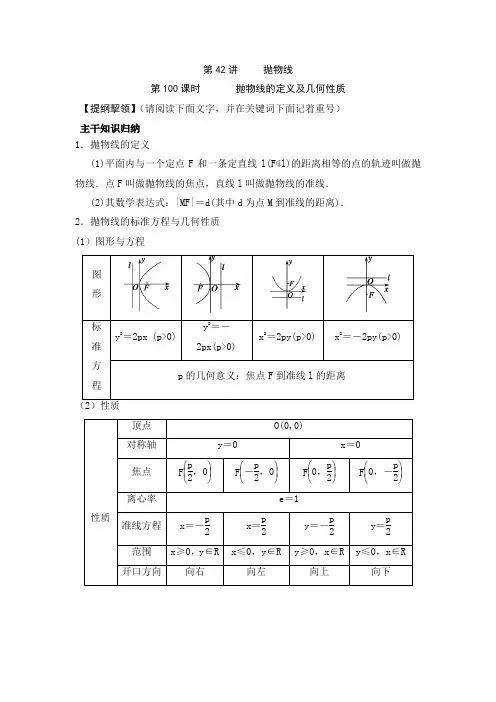
第42讲抛物线第100课时抛物线的定义及几何性质【提纲挈领】（请阅读下面文字，并在关键词下面记着重号）主干知识归纳1．抛物线的定义(1)平面内与一个定点F和一条定直线l(F∉l)的距离相等的点的轨迹叫做抛物线．点F叫做抛物线的焦点，直线l叫做抛物线的准线．(2)其数学表达式：|MF|＝d(其中d为点M到准线的距离)．2．抛物线的标准方程与几何性质(1）图形与方程2124p x x =；（212y p =-；13|)2sin p AB x x x =++=）以AB 为直径的原与准线（5）/090AC B ∠=； （6）//090A FB ∠=；（7）A 、O 、/B 三点共线；（8）B 、O 、/A 三点共线； （9）112||||AF BF P +=；（10）22sin ABOp Sα=等等。

方法规律总结1. 抛物线的定义是抛物线问题的本质，它能将两种距离(抛物线上的点到焦点的距离、抛物线上的点到准线的距离)进行等量转化．如果问题中涉及抛物线的焦点和准线，又能与距离联系起来，那么用抛物线定义就能解决问题．2.求抛物线标准方程的常用方法是待定系数法，其关键是判断焦点位置，开口方向，在方程的类型已经确定的前提下，由于标准方程只有一个参数p ，只需一个条件就可以确定抛物线的标准方程．3.在解决与抛物线的性质有关的问题时，要注意利用几何图形的形象、直观的特点来解题，特别是涉及焦点、顶点、准线的问题更是如此．【指点迷津】【类型一】抛物线的定义及其应用【例1】：已知点A (3，4)，F 是抛物线y 2＝8x 的焦点，M 是抛物线上的动点，当|AM |＋|MF |最小时，M 点坐标是( )A ．(0，0)B ．(3，26)C ．(2，4)D ．(3，－26)【解析】：由题知点A 在抛物线内．设M 到准线的距离为|MK |，则|MA |＋|MF |＝|MA |＋|MK |，当|MA |＋|MK |最小时，M 点坐标是(2，4)． 答案：C.【例2】：已知点A (2,0)，抛物线C ：x 2＝4y 的焦点为F ，射线FA 与抛物线C 相交于点M ，与其准线相交于点N ，则|FM |∶|MN |＝( )．A ．2∶ 5B ．1∶2C ．1∶ 5D ．1∶3【解析】：如图所示，由抛物线定义知|MF |＝|MH |，所以|MF |∶|MN |＝|MH |∶|MN |.由△MHN ∽△FOA ，则|MH ||HN |＝|OF ||OA |＝12， 则|MH |∶|MN |＝1∶5，即|MF |∶|MN |＝1∶ 5. 答案：C.【例3】：已知点P 是抛物线y 2＝4x 上的动点，点P 在y 轴上的射影是M ，点A 的坐标是(4，a )，则当|a |＞4时，|PA |＋|PM |的最小值是________． 【解析】：将x ＝4代入抛物线方程y 2＝4x ，得y ＝±4，|a |＞4，所以A 在抛物线的外部，由题意知F (1,0)，则抛物线上点P 到准线l ：x ＝－1的距离为|PN |，由定义知，|PA |＋|PM |＝|PA |＋|PN |－1＝|PA |＋|PF |－1.当A ，P ，F 三点共线时，|PA |＋|PF |取最小值，此时|PA |＋|PM |也最小，最小值为|AF |－1＝9＋a 2－1. 答案：9＋a 2－1.【类型二】抛物线的标准方程【例1】：如果抛物线的顶点在原点，对称轴为x 轴，焦点在直线3x －4y －12＝0上，那么抛物线的方程是( )A ．y 2＝－16xB ．y 2＝12xC ．y 2＝16xD ．y 2＝－12x【解析】：由题设知直线3x －4y －12＝0与x 轴的交点(4，0)即为抛物线的焦点，故其方程为y 2＝16x . 答案：C ．【例2】：已知圆x 2＋y 2＋mx －14＝0与抛物线y ＝14x 2的准线相切，则m ＝( )．A ．±2 2B. 3C. 2 D ．± 3【解析】：抛物线的标准方程为x 2＝4y ，所以准线为y ＝－1.圆的标准方程为⎝ ⎛⎭⎪⎫x ＋m 22＋y 2＝m 2＋14，所以圆心为⎝ ⎛⎭⎪⎫－m 2，0，半径为m 2＋12.所以圆心到直线的距离为1，即m 2＋12＝1，解得m ＝± 3.答案：D.【例3】：如图，过抛物线y 2＝2px (p >0)的焦点F 的直线交抛物线于点A ，B ，交其准线l 于点C ，若|BC |＝2|BF |，且|AF |＝3，则此抛物线的方程为( )．A ．y 2＝9xB ．y 2＝6xC ．y 2＝3xD ．y 2＝3x 【解析】：如图，分别过A ，B 作AA 1⊥l 于A 1，BB 1⊥l 于B 1， 由抛物线的定义知：|AF |＝|AA 1|，|BF |＝|BB 1|， ∵|BC |＝2|BF |，∴|BC |＝2|BB 1|，∴∠BCB 1＝30°，∴∠AF x ＝60°，连接A 1F ，则△AA 1F 为等边三角形，过F 作FF 1⊥AA 1于F 1，则F 1为AA 1的中点，设l 交x 轴于K ，则|KF |＝|A 1F 1|＝12|AA 1|＝12|AF |，即p ＝32，∴抛物线方程为y 2＝3x . 答案：C.【类型三】抛物线的几何性质【例1】：已知直线l 过抛物线C 的焦点，且与C 的对称轴垂直，l 与C 交于A 、B 两点，|AB |＝12，P 为C 的准线上一点，则△ABP 的面积为( )A ．18B ．24C ．36D ．48【解析】：设抛物线方程为y 2＝2px ，当x ＝p2时，y 2＝p 2， ∴|y |＝p .∴p ＝|AB |2＝122＝6，又点P 到AB 的距离始终为6，∴S △ABP ＝12×12×6＝36.故选C.答案：C.【例2】：已知抛物线y 2＝2px (p ＞0)的焦点F 与双曲线x 24－y 25＝1的右焦点重合，抛物线的准线与x 轴的交点为K ，点A 在抛物线上且|AK |＝2|AF |，则A 点的横坐标为( )．A ．2 2B ．3C ．2 3D ．4【解析】：抛物线的焦点为⎝ ⎛⎭⎪⎫p 2，0，准线为x ＝－p 2.双曲线的右焦点为(3,0)，所以p2＝3，即p ＝6，即y 2＝12x .过A 做准线的垂线，垂足为M ，则|AK |＝2|AF |＝2|AM |，即|KM |＝|AM |，设A (x ，y )，则y ＝x ＋3，代入y 2＝12x ，解得x ＝3. 答案：B.【例3】：过抛物线y 2＝4x 的焦点F 的直线交该抛物线于A ，B 两点．若|AF |＝3，则|BF |＝________.【解析】：法一 由1|AF |＋1|BF |＝2p .得|BF |＝32.法二 设∠BFO ＝θ，则⎩⎨⎧|AF |＝p ＋|AF |cos θ，|BF |＝p －|BF |cos θ，由|AF |＝3，p ＝2，得cos θ＝13，∴|BF |＝32. 答案：32.【同步训练】【一级目标】基础巩固组 一、选择题1．抛物线y 2＝4x 的焦点到双曲线x 2－y 23＝1的渐近线的距离是( )．A.12B.32C ．1 D.3 【解析】：抛物线y 2＝4x 的焦点F (1,0)，双曲线x 2－y 23＝1的渐近线方程是y ＝±3x ，即3x ±y ＝0，故所求距离为|3±0|32＋2＝32. 答案：B.2．已知圆x 2＋y 2－6x －7＝0与抛物线y 2＝2px (p ＞0)的准线相切，则p 的值为( )．A ．1B ．2 C.12D ．4【解析】：圆的标准方程为(x －3)2＋y 2＝16，圆心为(3,0)，半径为4.圆心到准线的距离为3－⎝ ⎛⎭⎪⎫－p 2＝4，解得p ＝2.答案：B.3．点M (5,3)到抛物线y ＝ax 2的准线的距离为6，那么抛物线的方程是( )． A ．y ＝12x 2 B ．y ＝12x 2或y ＝－36x 2C ．y ＝－36x 2 D ．y ＝112x 2或y ＝－136x 2 【解析】：分两类a >0，a <0可得y ＝112x 2，y ＝－136x 2. 答案：D.4．已知抛物线y 2＝2px (p ＞0)的准线与圆(x －3)2＋y 2＝16相切，则p 的值为( )A.12B ．1C ．2D ．4 【解析】：由题知抛物线的准线为x ＝－p2，圆心为(3，0)、半径为4，由准线与圆相切得圆心到准线的距离d ＝3＋p2＝4，解得p ＝2.答案：C.5．已知双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的两条渐近线与抛物线y 2＝2px (p >0)的准线分别交于A ，B 两点，O 为坐标原点．若双曲线的离心率为2，△AOB 的面积为3，则p ＝( )． A ．1 B.32C ．2D ．3【解析】：由已知得双曲线离心率e ＝c a＝2，得c 2＝4a 2，∴b 2＝c 2－a 2＝3a 2，即b ＝3a .又双曲线的渐近线方程为y ＝±ba x ＝±3x ，抛物线的准线方程为x ＝－p2，所以不妨令A ⎝ ⎛⎭⎪⎫－p 2，32p ，B ⎝ ⎛⎭⎪⎫－p 2，－3p 2，于是|AB |＝3p .由△AOB 的面积为3可得12·3p ·p 2＝3，所以p 2＝4，解得p ＝2或p ＝－2(舍去)．答案：C. 二、填空题6．若点P 到直线y ＝－1的距离比它到点(0,3)的距离小2，则点P 的轨迹方程是________．【解析】：由题意可知点P 到直线y ＝－3的距离等于它到点(0,3)的距离，故点P 的轨迹是以点(0,3)为焦点，以y ＝－3为准线的抛物线，且p ＝6，所以其标准方程为x 2＝12y . 答案：x 2＝12y.7．已知抛物线y 2＝4x 上一点M 与该抛物线的焦点F 的距离|MF |＝4，则点M 的横坐标x 0＝________.【解析】：抛物线y 2＝4x 的焦点为F (1,0)，准线为x ＝－1. 根据抛物线的定义，点M 到准线的距离为4，则M 的横坐标为3. 答案：3.8．抛物线x 2＝2py (p ＞0)的焦点为F ，其准线与双曲线x 23－y 23＝1相交于A ，B 两点，若△ABF 为等边三角形，则p ＝________. 【解析】：如图，在等边三角形ABF 中，DF ＝p ，BD ＝33p ， ∴B 点坐标为⎝ ⎛⎭⎪⎫33p ，－p2.又点B 在双曲线上，故13p 23－p 243＝1.解得p ＝6.答案：6. 三、解答题9．已知抛物线的顶点在原点，对称轴是x 轴，抛物线上的点M (－3，m )到焦点的距离为5，求抛物线的方程和m 的值．【解析】：法一：根据已知条件，抛物线方程可设为y 2＝－2px (p ＞0)，则焦点F ⎝ ⎛⎭⎪⎫－p 2，0.∵点M (－3，m )在抛物线上，且|MF |＝5，故⎩⎨⎧m 2＝6p ，⎝⎛⎭⎪⎫－3＋p 22＋m 2＝5，解得⎩⎨⎧p ＝4，m ＝26或⎩⎨⎧p ＝4，m ＝－2 6.∴抛物线方程为y 2＝－8x ，m ＝±2 6.法二：设抛物线方程为y 2＝－2px (p >0)，则准线方程为x ＝p2，由抛物线定义，M点到焦点的距离等于M 点到准线的距离，所以有p2－(－3)＝5，∴p ＝4.∴所求又∵点M (－3，m )在抛物线上，故m 2＝(－8)×(－3)，∴抛物线方程为y 2＝－8x ，m ＝±2 6.答案：抛物线方程为y 2＝－8x ，m ＝±2 6.10.已知倾斜角为θ的直线过抛物线y 2＝2px(p>0)的焦点F ，与抛物线交于A 、B 两点，求证：(1)|AB|＝2p sin 2θ； (2)S △AOB ＝p 22sin θ； (3)以AB 为直径的圆与抛物线的准线相切．【解析】:(1)由抛物线的定义知|AF|等于点A 到准线x ＝－p2的距离，所以|AF|＝x 1＋p 2.同理，|BF|＝x 2＋p2.所以|AB|＝|AF|＋|BF|＝x 1＋x 2＋p ①又设焦点弦的方程为y ＝k(x －p 2)(k≠0)，所以x ＝1k y ＋p2，故x 1＋x 2＝1k (y 1＋y 2)＋p.y 2－2p k y －p 2＝0，y 1＋y 2＝2p k .所以x 1＋x 2＝2pk2＋p ② 将②代入①得：|AB|＝2p k 2＋2p ＝2p(1＋1k 2)＝2p(1＋1tan 2θ)＝2psin 2θ(2)如图，S △AOB ＝S △AOF ＋S △BOF ＝12|OF|·|AF|·sin(π－θ)＋12|OF|·|BF|·sin θ＝12|OF|·sin θ(|AF|＋|BF|)＝12|OF|·|AB|·sin θ＝12·p 2·2p sin 2θ·sin θ＝p 22sin θ. (3)设线段AB 的中点为M ，分别过A 、M 、B 作准线的垂线，垂足为C 、N 、D ，则|MN|＝12(|AC|＋|BD|)＝12(|AF|＋|BF|)＝12|AB|.所以以AB 为直径的圆与准线相切． 答案:略.【二级目标】能力提升题组 一、选择题1．已知双曲线C 1：x 2a 2－y 2b 2＝1(a >0，b >0)的离心率为2.若抛物线C 2：x 2＝2py (p >0)的焦点到双曲线C 1的渐近线的距离为2，则抛物线C 2的方程为( )．A ．x 2＝833y B ．x 2＝1633y C ．x 2＝8y D ．x 2＝16y 【解析】：∵x 2a 2－y 2b 2＝1的离心率为2，∴c a ＝2，即c 2a 2＝a 2＋b 2a 2＝4，∴ba ＝ 3.x 2＝2py 的焦点坐标为⎝⎛⎭⎪⎫0，p 2，x 2a 2－y 2b 2＝1的渐近线方程为y ＝±b a x ，即y ＝±3x .由题意，得p21＋32＝2，∴p ＝8.故C 2：x 2＝16y ，选D. 答案：D.2．(2014·洛阳统考)已知P 是抛物线y 2＝4x 上一动点，则点P 到直线l ：2x －y ＋3＝0和y 轴的距离之和的最小值是( )．A. 3B. 5 C ．2 D.5－1【解析】：由题，抛物线的焦点为F (1,0)．设点P 到直线l 的距离为d ，由抛物线的定义可知，点P 到y 轴的距离为|PF |－1，所以点P 到直线l 的距离与到y 轴的距离之和为d ＋|PF |－1.易知d ＋|PF |的最小值为点F 到直线l 的距离，故d ＋|PF |的最小值为22)1(2|32|-++＝5，所以d ＋|PF |－1的最小值为5－1.答案：D. 二、填空题3．已知椭圆C ：x 24＋y 23＝1的右焦点为F ，抛物线y 2＝4x 的焦点为F ，准线为l ，P 为抛物线上一点，PA ⊥l ，A 为垂足．如果直线AF 的倾斜角为120°，那么|PF |＝________.【解析】:抛物线的焦点坐标为F (1,0)，准线方程为x ＝－1.因为直线AF 的倾斜角为120°，所以tan 120°＝y A －1－1，所以y A ＝2 3.因为PA ⊥l ，所以y P ＝y A＝23，代入y 2＝4x ，得x A ＝3，所以|PF |＝|PA |＝3－(－1)＝4. 答案：4. 三、解答题4. 如图,抛物线()2212:4,:20C x y C x py p ==->,点()00,M x y 在抛物线2C 上,过M 作1C 的切线,切点为,A B (M 为原点O 时,,A B 重合于O)01x =,切线.MA 的斜率为12-.(I)求p 的值;(II)当M 在2C 上运动时,求线段AB 中点N 的轨迹方程.(),,.A B O O 重合于时中点为③,【高考链接】1.（2010年全国Ⅱ卷理15文15）已知抛物线2:2(0)C y px p =＞的准线为l ，过(1,0)M l 相交于点A ，与C 的一个交点为B ．若AM MB =，则p = ．【解析】：过B 作BE 垂直于准线l 于E ，∵AM MB =，∴M 为中点，∴1BM AB 2=0BAE 30∠=， ∴1BE AB 2=，∴BM BE =，∴M 为抛物线的焦点，∴p =2. 答案:2.2.（2009年广东理科第19题）已知曲线2:C y x =与直线:20l x y -+=交于两点(,)A A A x y 和(,)B B B x y ，且A B x x <．记曲线C 在点A 和点B 之间那一段L 与线段AB 所围成的平面区域（含边界）为D ．设点(,)P s t 是L 上的任一点，且点P 与点A 和点B 均不重合．（１）若点Q 是线段AB 的中点，试求线段PQ 的中点M 的轨迹方程；（２）若曲线22251:24025G x ax y y a -+-++=与点D 有公共点，试求a 的最小值． 【解析】：（1）联立2x y =与2+=x y 得2,1=-=B A x x ，则AB 中点)25,21(Q ，设线段PQ 的中点M 坐标为),(y x ，则225,221ty s x +=+=，即252,212-=-=y t x s ，又点P 在曲线C 上，∴2)212(252-=-x y 化简可得8112+-=x x y ，又点P 是L 上的任一点，且不与点A 和点B 重合，则22121<-<-x ，即4541<<-x ，∴中点M 的轨迹方程为8112+-=x x y （4541<<-x ）.（2）曲线22251:24025G x ax y y a -+-++=，即圆E ：2549)2()(22=-+-y a x ，其圆心坐标为)2,(a E ，半径57=r由图可知，当20≤≤a 时，曲线22251:24025G x ax y y a -+-++=与点D 有公共点；当0<a 时，要使曲线22251:24025G x ax y y a -+-++=与点D 有公共点，只需圆心E 到直线:20l x y -+=的距离572||2|22|≤=+-=a a d ，得0527<≤-a ，则a 的最小值为527-.答案: （1） M 的轨迹方程为8112+-=x x y （4541<<-x ）. （2） a 的最小值为527-.3.（2013年福建数学（理））如图,在正方形OABC 中,O 为坐标原点,点A 的坐标为(10,0),点C 的坐标为(0,10).分别将线段OA 和AB 十等分,分点分别记为129,,....A A A 和129,,....B B B ,连结i OB ,过i A 做x 轴的垂线与i OB 交于点*(,19)i P i N i ∈≤≤.(1)求证:点*(,19)i P i N i ∈≤≤都在同一条抛物线上,并求该抛物线E 的方程; (2)过点C 做直线与抛物线E 交于不同的两点,M N ,若OCM ∆与OCN ∆的面积比为4:1,求直线的方程.【解析】：(Ⅰ)依题意,过*(,19)∈≤≤i A i N i 且与x 轴垂直的直线方程为=x i(10,)i B i ,∴直线i OB 的方程为10=iy x 设i P 坐标为(,)x y ,由10=⎧⎪⎨=⎪⎩x iiy x 得:2110=y x ,即210=x y , ∴*(,19)∈≤≤i P i N i 都在同一条抛物线上,且抛物线E 方程为210=x y(Ⅱ)依题意:直线的斜率存在,设直线的方程为10=+y kx由21010=+⎧⎨=⎩y kx x y得2101000--=x kx [来源:学*科*网] 此时2100+4000∆=>k ,直线与抛物线E 恒有两个不同的交点,M N设:1122(,)(,)M x y N x y ,则121210100+=⎧⎨⋅=-⎩x x kx x4∆∆=OCM OCN S S ∴124=x x 又120⋅<x x ,∴124=-x x 分别代入21010=+⎧⎨=⎩y kx x y,解得32=±k 直线的方程为3+102=±y x ,即32200-+=x y 或3+2200-=x y .答案: (Ⅰ) 抛物线E 方程为210=x y ;(Ⅱ) 直线的方程为 32200-+=x y 或3+2200-=x y .。

教学内容 抛物线1．抛物线的定义满足以下三个条件的点的轨迹是抛物线： (1)在平面内；(2)动点到定点F 距离与到定直线l 的距离相等； (3)定点不在定直线上．2．抛物线的标准方程和几何性质标准方程y 2＝2px (p ＞0)y 2＝－2px (p ＞0)x 2＝2py (p >0)x 2＝－2py (p >0)p 的几何意义：焦点F 到准线l 的距离图形顶点 O (0,0)对称轴 y ＝0x ＝0焦点 F (p2，0) F (－p2，0)F (0，p 2)F (0，－p2)离心率 e ＝1准线 方程 x ＝－p 2x ＝p 2 y ＝－p 2y ＝p 2 范围 x ≥0，y ∈Rx ≤0，y ∈Ry ≥0，x ∈Ry ≤0，x ∈R开口方向 向右 向左 向上 向下 焦半径(其中P (x 0，y 0)|PF |＝x 0＋p2|PF |＝－x 0＋p2|PF |＝y 0＋p2|PF |＝－y 0＋p21．抛物线的定义中易忽视“定点不在定直线上”这一条件，当定点在定直线上时，动点的轨迹是过定点且与直线垂直的直线．2．抛物线标准方程中参数p 易忽视只有p ＞0，才能证明其几何意义是焦点F 到准线l 的距离，否则无几何意义． [试一试]1．抛物线y 2＝8x 的焦点到准线的距离是________．2．动圆过点(1,0)，且与直线x ＝－1相切，则动圆的圆心的轨迹方程为________．1．转化思想在定义中应用抛物线上点到焦点距离常用定义转化为点到准线的距离． 2．与焦点弦有关的常用结论 (以下图为依据)(1)y 1y 2＝－p 2，x 1x 2＝p 24. (2)|AB |＝x 1＋x 2＋p ＝2psin 2θ(θ为AB 的倾斜角)．(3)1|AF |＋1|BF |为定值2p. (4)以AB 为直径的圆与准线相切． (5)以AF 或BF 为直径的圆与y 轴相切． [练一练]1．若抛物线x 2＝ay 过点A ⎝⎛⎭⎫1，14，则点A 到此抛物线的焦点的距离为________．2．已知过抛物线y 2＝4x 的焦点F 的直线交该抛物线于A ，B 两点，O 是坐标原点，|AF |＝2，则|BF |＝________，△OAB 的面积是________．考点一抛物线的标准方程及几何性质1.(2013·南通、扬州、泰州二模)若抛物线y2＝2px(p>0)上的点A(2，m)到焦点的距离为6，则p＝________.2．(2013·苏州模底)抛物线y2＝4x的准线方程是________．3．从抛物线x2＝4y上一点P引抛物线准线的垂线，垂足为M，且|PM|＝5，设抛物线的焦点为F，则△MPF的面积为________．[类题通法]1．涉及抛物线几何性质的问题常结合图形思考，通过图形可以直观地看出抛物线的顶点、对称轴、开口方向等几何特征，体现了数形结合思想解题的直观性．2．求抛物线方程应注意的问题(1)当坐标系已建立时，应根据条件确定抛物线方程属于四种类型中的哪一种；(2)要注意把握抛物线的顶点、对称轴、开口方向与方程之间的对应关系；(3)要注意参数p的几何意义是焦点到准线的距离，利用它的几何意义来解决问题．考点二抛物线的定义应用与抛物线定义相关的最值问题常涉及距离最短、距离和最小等等.归纳起来常见的命题角度有：(1)动弦中点到坐标轴距离最短问题；(2)距离之和最小问题；(3)焦点弦中距离之和最小问题.角度一动弦中点到坐标轴距离最短问题1．已知抛物线x2＝4y上有一条长为6的动弦AB，则AB的中点到x轴的最短距离为________．角度二距离之和最小问题2．(2014·哈尔滨四校统考)已知抛物线方程为y2＝4x，直线l的方程为x－y＋5＝0，在抛物线上有一动点P到y轴的距离为d1，到直线l的距离为d2，则d1＋d2的最小值为________．角度三焦点弦中距离之和最小问题3．已知抛物线y2＝4x，过焦点F的直线与抛物线交于A、B两点，过A、B分别作y轴垂线，垂足分别为C、D，则|AC|＋|BD|的最小值为________．[类题通法]与抛物线有关的最值问题的解题策略该类问题一般情况下都与抛物线的定义有关．实现由点到点的距离与点到直线的距离的转化．(1)将抛物线上的点到准线的距离转化为该点到焦点的距离，构造出“两点之间线段最短”，使问题得解．(2)将抛物线上的点到焦点的距离转化为到准线的距离，利用“与直线上所有点的连线中垂线段最短”原理解决．考点三直线与抛物线的位置关系[典例](2014·无锡期末)如图，过抛物线y2＝2px(p>0)的焦点F的直线l交抛物线于A，B两点，交其准线于点C.若BC＝2BF，且AF＝3，则此抛物线的方程为________．[类题通法]求解直线与抛物线位置关系问题的方法在解决直线与抛物线位置关系的问题时，其方法类似于直线与椭圆的位置关系．在解决此类问题时，除考虑代数法外，还应借助平面几何的知识，利用数形结合的思想求解．[针对训练](2014·南京摸底)已知抛物线y2＝4x的焦点为F，准线为l.过点F作倾斜角为60°的直线与抛物线在第一象限的交点为A，过点A作l的垂线，垂足为A1，则△AA1F的面积是________．[课堂练通考点]1．(2013·镇江期末)圆心在抛物线x2＝2y上，并且和抛物线的准线及y轴都相切的圆的标准方程为________．2．设抛物线y2＝6x的焦点为F，准线为l，P为抛物线上一点，P A⊥l，垂足为A，如果△APF为正三角形，那么|PF|等于________．3．过抛物线y2＝8x的焦点F作倾斜角为135°的直线交抛物线于A，B两点，则弦AB的长为________．9．(2013·天津调研)设F是抛物线C1：y2＝2px(p>0)的焦点，点A是抛物线与双曲线C2：x2a2－y2b2＝1(a>0，b>0)的一条渐近线的一个公共点，且AF⊥x轴，则双曲线的离心率为________．10．已知抛物线y2＝2px(p>0)上一点M(1，m)(m>0)到其焦点F的距离为5，该抛物线的顶点在直线MF 上的射影为点P，则点P的坐标为________．第Ⅱ组：重点选做题1．(2013·苏北四市二调)已知点A(0,2)，抛物线y2＝2px(p>0)的焦点为F，准线为l，线段F A交抛物线于点B，过B作l的垂线，垂足为M，若AM⊥MF，则p＝________.2．已知过点P(4,0)的直线与抛物线y2＝4x相交于A(x1，y1)，B(x2，y2)两点，则y21＋y22的最小值是________．3．(2014·荆州模拟)如图，直线AB经过抛物线y2＝2px的焦点F，交抛物线于点A、B，交抛物线的准线l于点C，若BC＝－2BF，且|AF|＝3，则此抛物线的方程为________．4．(2014·黄冈月考)如图，A1，A2，A3，…，A n分别是抛物线y＝x2上的点，A1B1垂直于x轴，A1C1垂直于y轴，线段B1C1交抛物线于A2，再作A2B2⊥x轴，A2C2⊥y轴，线段B2C2交抛物线于A3，这样下去，分别可以得到A4，A5，…，A n，其中A1的坐标为(1,1)，则S矩形A n B n OC n＝________.。

学案7 抛物线
考纲解读 考向预测 课前热身
考点突破
即时巩固 课后拔高
考点 四 考点 三 考点 二 考点 一
真题再现 误区警示 规律探究
考纲解读
返回
考点 一
考点突破
返回
返回
返回
返回
返回
返回
考点 二
返回
返回
返回
返回
返回
考点 三
返回
返回
返回
返回
考点 四
返回
返回
返回
真题再现
返回
返回
误区警示
返回
规律探究
返回
即时巩固
返回
返回
返回
返回
返回
课后拔高
返回
返回
返回
返回
返回
返回
返回
返回
返回
返回
返回
返回
返回
返回
返回
返回
返回
返回
返回
返回

高考数学第一轮复习：《抛物线》最新考纲1.掌握抛物线的定义、几何图形、标准方程及简单几何性质(范围、对称性、顶点、离心率).2.理解数形结合思想．3.了解抛物线的简单应用.【教材导读】1．若抛物线定义中定点F 在定直线l 上时，动点的轨迹是什么图形？提示：当定点F 在定直线l 上时，动点的轨迹是过点F 且与直线l 垂直的直线． 2．抛物线的标准方程中p 的几何意义是什么？ 提示：p 的几何意义是焦点到准线的距离．1．抛物线的定义平面内与一个定点F 和一条定直线l (l 不经过点F )距离相等的点的轨迹叫做抛物线．点F 叫做抛物线的焦点，直线l 叫做抛物线的准线．2．抛物线的标准方程及其简单几何性质标准 方程 y 2＝2px (p >0)y 2＝－2px (p >0)x 2＝2py (p >0)x 2＝－2py (p >0)图形顶点 (0,0)对称轴 x 轴y 轴焦点 F ⎝ ⎛⎭⎪⎫p 2，0 F ⎝ ⎛⎭⎪⎫－p 2，0 F ⎝ ⎛⎭⎪⎫0，p 2 F ⎝ ⎛⎭⎪⎫0，－p 2 离心率 e ＝1准线方程x ＝－p 2x ＝p 2y ＝－p2y ＝p 2【重要结论】抛物线焦点弦的几个常用结论设AB 是过抛物线y 2＝2px (p >0)焦点F 的弦，若A (x 1，y 1)，B (x 2，y 2)，则 (1)x 1x 2＝p 24，y 1y 2＝－p 2.(2)弦长|AB |＝x 1＋x 2＋p ＝2psin 2 α(α为弦AB 的倾斜角)． (3)以弦AB 为直径的圆与准线相切．(4)通径：过焦点垂直于对称轴的弦，长等于2p .1．已知抛物线y 2＝2px (p >0)的准线经过点(－1,1)，则该抛物线焦点坐标为( ) (A)(－1,0) (B)(1,0) (C)(0，－1)(D)(0,1)B 解析：由准线过已知点可求出p 的值，进而可求出抛物线的焦点坐标．抛物线y 2＝2px (p >0)的准线为x ＝－p 2且过点(－1,1)，故－p2＝－1，解得p ＝2.所以抛物线的焦点坐标为(1,0)．2．若点P 为抛物线y ＝2x 2上的动点，F 为抛物线的焦点，则|PF |的最小值为( ) (A)2 (B)12 (C)14(D)18D 解析：本题考查抛物线的定义．抛物线y ＝2x 2上的点到焦点的距离等于该点到准线的距离，所以最小距离是p 2，又2p ＝12，则p 2＝18，即|PF |的最小值为18，故选D.3．已知AB 是抛物线y 2＝2x 的一条焦点弦，|AB |＝4，则AB 中点C 的横坐标是( ) (A)2 (B)12 (C)32(D)52C 解析：设A (x 1，y 1)，B (x 2，y 2)，则|AB |＝x 1＋x 2＋p ＝4， 又p ＝1，所以x 1＋x 2＝3， 所以点C 的横坐标是x 1＋x 22＝32.4．设抛物线y 2＝2px (p >0)的焦点为F ，点A (0,2)，若线段F A 的中点B 在抛物线上，则B 到该抛物线准线的距离为________．解析：依题意知F 坐标为p2，0， 所以B 的坐标为p4，1代入抛物线方程得 p 22＝1，解得p ＝2，所以抛物线准线方程为x ＝－22，所以点B 到抛物线准线的距离为24＋22＝34 2. 答案：34 25．直线l 过抛物线x 2＝2py (p ＞0)的焦点，且与抛物线交于A ，B 两点，若线段AB 的长是6，AB 的中点到x 轴的距离是1，则此抛物线方程是________．解析：设A (x 1，y 1)，B (x 2，y 2)，则|AB |＝y 1＋y 2＋p ＝2＋p ＝6，∴p ＝4.即抛物线方程为x 2＝8y .答案：x 2＝8y考点一 抛物线的定义及其应用(1)长为2的线段AB 的两个端点在抛物线y 2＝x 上滑动，则线段AB 的中点M到y 轴距离的最小值是________．(2)已知点P 是抛物线y 2＝4x 上的动点，点P 在y 轴上的射影是M ，点A 的坐标是(4，a )，则当|a |＞4时，|P A |＋|PM |的最小值是________．(3)已知抛物线y 2＝4x ，过焦点F 的直线与抛物线交于A ，B 两点，过A ，B 分别作y 轴的垂线，垂足分别为C ，D ，则|AC |＋|BD |的最小值为________．解析：(1)如图，AB＝2，要使AB的中点M到y轴的距离最小，则|BG|＋|AE|的值最小，即|AF|＋|BF|的值最小．在△ABF中，|AF|＋|BF|≥|AB|，当A，B，F三点共线时取等号，即当线段AB过焦点F时，AB的中点M到y轴的距离最小，最小值为|AE|＋|BG|2－14＝1－14＝34.(2)将x＝4代入抛物线的方程y2＝4x，得y＝±4.又|a|＞4，所以点A在抛物线的外部．由题意知F(1,0)，设抛物线上点P到准线l：x＝－1的距离为|PN|，由定义知，|P A|＋|PM|＝|P A|＋|PN|－1＝|P A|＋|PF|－1.画出简图(图略)，易知当A，P，F三点共线时，|P A|＋|PF|取得最小值，此时|P A|＋|PM|也最小，最小值为|AF|－1＝9＋a2－1.(3)由题意知F(1,0)，|AC|＋|BD|＝|AF|＋|FB|－2＝|AB|－2.依据抛物线的定义知，当|AB为通径，即|AB|＝2p＝4时，|AB|的值最小，所以|AC|＋|BD|的最小值为2.答案：(1)34(2)9＋a2－1(3)2【反思归纳】利用抛物线的定义可解决的常见问题(1)轨迹问题：用抛物线的定义可以确定动点与定点、定直线距离有关的轨迹是否为抛物线．(2)距离问题：涉及抛物线上的点到焦点的距离和到准线的距离问题时，注意在解题中利用两者之间的相互转化．【即时训练】(1)已知抛物线方程为y2＝4x，直线l的方程为x－y＋4＝0，在抛物线上有一动点P到y轴的距离为d1，P到直线l的距离为d2，则d1＋d2的最小值是()(A)522＋2 (B)522＋1 (C)522－2(D)522－1(2)若点A 的坐标为(3,2)，F 是抛物线y 2＝2x 的焦点，点M 在抛物线上移动时，使|MF |＋|MA |取得最小值的M 的坐标为( )(A)(0,0) (B)⎝ ⎛⎭⎪⎫12，1 (C)(1，2)(D)(2,2)解析：(1)如图，点P 到准线的距离等于点P 到焦点F 的距离，从而P 到y 轴的距离等于点P 到焦点F 的距离减1，过焦点F 作直线x －y ＋4＝0的垂线，此时d 1＋d 2＝|PF |＋d 2－1最小．因为F (0,1)，则|PF |＋d 2＝|1－0＋4|1＋1＝522，则d 1＋d 2的最小值为522－1.(2)过M 点作左准线的垂线，垂足是N ，则|MF |＋|MA |＝|MN |＋|MA |，当A ，M ，N 三点共线时，|MF |＋|MA |取得最小值，此时M (2,2)．故选D.答案：(1)D (2)D考点二 抛物线的标准方程及性质(1)已知抛物线y 2＝2px (p ＞0)上一点M 到焦点F 的距离等于2p ，则直线MF 的斜率为( )(A)±3 (B)±1 (C)±34(D)±33(2)过抛物线y 2＝4x 的焦点F 的直线l 与抛物线交于A ，B 两点，若A ，B 两点的横坐标之和为103，则|AB |＝( )(A)133 (B)143 (C)5(D)163(3)过抛物线C ：x 2＝2y 的焦点F 的直线l 交抛物线C 于A 、B 两点，若抛物线C 在点B 处的切线斜率为1，则|AF |＝( )(A)1 (B)2 (C)3(D)4解析：(1)设M (x 0，y 0)，易知焦点为F ⎝ ⎛⎭⎪⎫p 2，0，由抛物线的定义得|MF |＝x 0＋p 2＝2p ，所以x 0＝32p ，故y 20＝2p ×32p ＝3p 2，解得y 0＝±3p ，故直线MF 的斜率k ＝±3p 32p －p 2＝±3，选A. (2)∵p ＝2，∴|AB |＝2＋103＝163.故选D. (3)∵x 2＝2y ，∴y ＝x 22，∴y ′＝x ，∵抛物线C 在点B 处的切线斜率为1， ∴B ⎝ ⎛⎭⎪⎫1，12 ∵抛物线x 2＝2y 的焦点F 的坐标为⎝ ⎛⎭⎪⎫0，12，∴直线l 的方程为y ＝12， ∴|AF |＝|BF |＝1.故选A. 答案：(1)A (2)D (3)A【反思归纳】 (1)抛物线几何性质的确定由抛物线的方程可以确定抛物线的开口方向、焦点位置、焦点到准线的距离；从而进一步确定抛物线的焦点坐标及准线方程．(2)求抛物线的标准方程的方法①因为抛物线方程有四种上标准形式，因此求抛物线方程时，需先定位，再定量．②因为未知数只有p，所以只需利用待定系数法确定p值即可．提醒：求标准方程要先确定形式，必要时要进行分类讨论，标准方程有时可设为y2＝mx 或x2＝my(m≠0)．【即时训练】(1)如图，过抛物线y2＝2px(p＞0)的焦点F的直线依次交抛物线及准线于点A，B，C，若|BC|＝2|BF|，且|AF|＝3，则抛物线的方程为()(A)y2＝3 2x(B)y2＝3x(C)y2＝9 2x(D)y2＝9x(2)若双曲线C：2x2－y2＝m(m＞0)与抛物线y2＝16x的准线交于A，B两点，且|AB|＝43，则m的值是________．答案：(1)B(2)20考点三直线与抛物线的位置关系考查角度1：直线与抛物线的交点问题．如图，已知抛物线C：y2＝2px(p＞0)，焦点为F，过点G(p,0)作直线l交抛物线C 于A ，M 两点，设A (x 1，y 1)，M (x 2，y 2)．(1)若y 1y 2＝－8，求抛物线C 的方程；(2)若直线AF 与x 轴不垂直，直线AF 交抛物线C 于另一点B ，直线BG 交抛物线C 于另一点N .求证：直线AB 与直线MN 斜率之比为定值．解：(1)设直线AM 的方程为x ＝my ＋p ，代入y 2＝2px 得y 2－2mpy －2p 2＝0， 则y 1y 2＝－2p 2＝－8，得p ＝2. ∴抛物线C 的方程为y 2＝4x . (2)证明：设B (x 3，y 3)，N (x 4，y 4)． 由(1)可知y 3y 4＝－2p 2，y 1y 3＝－p 2. 又直线AB 的斜率k AB ＝y 3－y 1x 3－x 1＝2p y 1＋y 3，直线MN 的斜率k MN ＝y 4－y 2x 4－x 2＝2py 2＋y 4，∴k AB k MN ＝y 2＋y 4y 1＋y 3＝－2p 2y 1＋－2p 2y 3y 1＋y 3＝－2p 2y 1y 3(y 1＋y 3)y 1＋y 3＝2.故直线AB 与直线MN 斜率之比为定值． 【反思归纳】 直线与抛物线位置关系的判断直线y ＝kx ＋m (m ≠0)或x ＝my ＋n 与抛物线y 2＝2px (p >0)联立方程组，消去y ，得到k 2x 2＋2(mk －p )x ＋m 2＝0的形式．当k ＝0时，直线和抛物线相交，且与抛物线的对称轴平行，此时与抛物线只有一个交点；当k ≠0时，设其判别式为Δ，(1)相交：Δ>0⇔直线与抛物线有两个交点； (2)相切：Δ＝0⇔直线与抛物线有一个交点； (3)相离：Δ<0⇔直线与抛物线没有交点．提醒：过抛物线外一点总有三条直线和抛物线有且只有一个公共点；两条切线和一条平行于对称轴的直线．考查角度2：直线与抛物线的相交弦问题设抛物线C ：y 2＝2px (p ＞0)的焦点为F ，准线为l .已知点A 在抛物线C 上，点B 在l 上，△ABF 是边长为4的等边三角形．(1)求p 的值；(2)在x 轴上是否存在一点N ，当过点N 的直线与抛物线C 交于Q 、R 两点时，1|NQ |2＋1|NR |2为定值？若存在，求出点N 的坐标，若不存在，请说明理由．解析：(1)由题知，|AF |＝|AB |，则AB ⊥l .设准线与x 轴交于点D ，则AB ∥DF .又△ABF 是边长为4的等边三角形，∠ABF ＝60°，所以∠BFD ＝60°，|DF |＝|BF |·cos ∠BFD ＝4×12＝2，即p＝2.(2)设点N (t,0)，由题意知直线的斜率不为零， 设直线的方程为x ＝my ＋t ，点Q (x 1，y 1)，R (x 2，y 2)，由⎩⎪⎨⎪⎧x ＝my ＋t y 2＝4x 得，y 2－4my －4t ＝0，则Δ＝16m 2＋16t ＞0，y 1＋y 2＝4m ，y 1·y 2＝－4t .又|NQ |2＝(x 1－t )2＋y 21＝(my 1＋t －t )2＋y 21＝(1＋m 2)y 21，同理可得|NR |2＝(1＋m 2)y 22，则有1|NQ |2＋1|NR |2＝1(1＋m 2)y 21＋1(1＋m 2)y 22＝y 21＋y 22(1＋m 2)y 21y 22＝(y 1＋y 2)2－2y 1y 2(1＋m 2)y 21y 22＝16m 2＋8t 16(1＋m 2)t 2＝2m 2＋t (2m 2＋2)t2. 若1|NQ |2＋1|NR |2为定值，则t ＝2，此时点N (2,0)为定点． 又当t ＝2，m ∈R 时，Δ＞0，所以，存在点N (2,0)，当过点N 的直线与抛物线C 交于Q 、R 两点时，1|NQ |2＋1|NR |2为定值14.【反思归纳】 直线与抛物线相交问题处理规律(1)凡涉及抛物线的弦长、弦的中点、弦的斜率问题时都要注意利用根与系数的关系，避免求交点坐标的复杂运算．解决焦点弦问题时，抛物线的定义有广泛的应用，而且还应注意焦点弦的几何性质．(2)对于直线与抛物线相交、相切、中点弦、焦点弦问题，以及定值、存在性问题的处理，最好是作出草图，由图象结合几何性质做出解答．并注意“设而不求”“整体代入”“点差法”的灵活应用.抛物线的综合问题已知点M (－1,1)和抛物线C ：y 2＝4x ，过C 的焦点且斜率为k 的直线与C 交于A ，B 两点．若∠AMB ＝90°，则k ＝________.审题点拨关键点 所获信息 抛物线y 2＝4x 可求焦点坐标 ∠AMB ＝90°k MA ·k MB ＝－1解题突破：把∠AMB ＝90°转化为斜率之积为－1.解析：由题意知，抛物线的焦点坐标为F (1,0)，设直线方程为y ＝k (x －1)，直线方程与y 2＝4x 联立，消去y ，得k 2x 2－(2k 2＋4)x ＋k 2＝0.设A (x 1，y 1)，B (x 2，y 2)，则x 1x 2＝1，x 1＋x 2＝2k 2＋4k 2. 由M (－1,1)，得AM→＝(－1－x 1,1－y 1)，BM →＝(－1－x 2,1－y 2)．由∠AMB ＝90°，得AM →·BM →＝0，∴ (x 1＋1)(x 2＋1)＋(y 1－1)(y 2－1)＝0， ∴ x 1x 2＋(x 1＋x 2)＋1＋y 1y 2－(y 1＋y 2)＋1＝0. 又y 1y 2＝k (x 1－1)·k (x 2－1)＝k 2[x 1x 2－(x 1＋x 2)＋1]， y 1＋y 2＝k (x 1＋x 2－2)，∴ 1＋2k 2＋4k 2＋1＋k 2⎝ ⎛⎭⎪⎫1－2k 2＋4k 2＋1－k ⎝ ⎛⎭⎪⎫2k 2＋4k 2－2＋1＝0，整理得4k 2－4k ＋1＝0，解得k ＝2.答案：2命题意图：本题重点考查直线与抛物线的应用，考查考生的运算能力．课时作业基础对点练(时间：30分钟)1．若抛物线y 2＝4x 上一点P 到其焦点F 的距离为2，O 为坐标原点，则△OFP 的面积为( )(A)12 (B)1 (C)32(D)2B 解析：设P (x p ，y p )，由题可得抛物线焦点为F (1,0)，准线方程为x ＝－1，又点P 到焦点F 的距离为2，∴由定义知点P 到准线的距离为2，∴x P ＋1＝2，∴x P ＝1，代入抛物线方程得|y P |＝2，∴△OFP 的面积为S ＝12·|OF |·|y P |＝12×1×2＝1.故选B.2．若抛物线y ＝ax 2的焦点坐标是(0,1)，则a ＝( ) (A)1 (B)14 (C)2(D)12B 解析：因为抛物线方程为x 2＝1a y ，所以其焦点坐标为⎝ ⎛⎭⎪⎫0，14a ，则有14a ＝1，a ＝14，故选B.3．已知P 为抛物线y 2＝－6x 上一个动点，Q 为圆x 2＋(y －6)2＝14上一个动点，那么点P 到点Q 的距离与点P 到y 轴距离之和的最小值是( )(A)317－72(B)317－42 (C)317－12(D)317＋12B 解析：结合抛物线的定义知，P 到y 轴的距离为P 到焦点的距离减去32，则所求最小值为抛物线的焦点到圆心的距离减去半径及32，即62＋⎝ ⎛⎭⎪⎫322－12－32＝317－42，故选B.4．若点A，B在抛物线y2＝2px(p＞0)上，O是坐标原点，若正三角形OAB的面积为43，则该抛物线方程是()(A)y2＝233x(B)y2＝3x(C)y2＝23x(D)y2＝3 3xA解析：根据对称性，AB⊥x轴，由于正三角形的面积是43，故34AB2＝43，故AB＝4，正三角形的高为23，故可以设点A的坐标为(23，2)，代入抛物线方程得4＝43p，解得p＝33，故所求的抛物线方程为y2＝233x.故选A.5．已知直线l1：4x－3y＋7＝0和直线l2：x＝－2，抛物线y2＝8x上一动点P到直线l1和l2的距离之和的最小值是()(A) 5 (B)2 5(C)3 (D)3 5C解析：如图所示，过点P作PH1⊥l1，PH2⊥l2，连接PF，H1F，过F作FM⊥l1，交l1于M，由抛物线方程为y2＝8x，得l2为其准线，焦点为F(2,0)，由抛物线的定义可知|PH1|＋|PH2|＝|PH1|＋|PF|≥|FH1|≥|FM|＝|4×2－0＋7|42＋32＝3，故选C.6．已知抛物线C的顶点是原点O，焦点F在x轴的正半轴上，经过F的直线与抛物线C交于A ，B 两点，如果OA →·OB→＝－12，那么抛物线C 的方程为( )(A)x 2＝8y (B)x 2＝4y (C)y 2＝8x(D)y 2＝4xC 解析：由题意，设抛物线方程为y 2＝2px (p >0)， 直线方程为x ＝my ＋p2，联立⎩⎨⎧y 2＝2px ，x ＝my ＋p2，消去x 得y 2－2pmy －p 2＝0， 设A (x 1，y 1)，B (x 2，y 2)， 则y 1＋y 2＝2pm ，y 1y 2＝－p 2，得OA →·OB →＝x 1x 2＋y 1y 2＝my 1＋p 2my 2＋p 2＋y 1y 2＝m 2y 1y 2＋pm 2(y 1＋y 2)＋p 24＋y 1y 2＝－34p 2＝－12⇒p ＝4，即抛物线C 的方程为y 2＝8x .7．过抛物线y ＝14x 2的焦点F 作一条倾斜角为30°的直线交抛物线于A ，B 两点，则|AB |＝________.解析：依题意，设点A (x 1，y 1)，B (x 2，y 2)，题中的抛物线x 2＝4y 的焦点坐标是F (0,1)，直线AB 的方程为y ＝33x ＋1，即x ＝3(y －1)．由⎩⎪⎨⎪⎧x 2＝4y ，x ＝3(y －1)，消去x 得3(y －1)2＝4y ，即3y 2－10y ＋3＝0，y 1＋y 2＝103，|AB |＝|AF |＋|BF |＝(y 1＋1)＋(y 2＋1)＝y 1＋y 2＋2＝163.答案：1638．抛物线y 2＝2px (p ＞0)的焦点为F ，AB 为抛物线上的两点，以AB 为直径的圆过点F ，过AB 的中点M 作抛物线的准线的垂线MN ，垂足为N ，则|MN ||AB |的最大值为__________．解析：由抛物线定义得|MN ||AB |＝|AF |＋|BF |2|AF |2＋|BF |2≤|AF |2＋|BF |22|AF |2＋|BF |2＝22，即|MN ||AB |的最大值为22.答案： 229．过抛物线y 2＝4x 的焦点F 的直线交抛物线于A ，B 两点，若|AF |＝5，则|BF |＝________. 解析：由题意，设A (x 1，y 1)，B (x 2，y 2)， 则|AF |＝x 1＋1＝5⇒x 1＝4，y 21＝4x 1＝16， 根据对称性，不妨取y 1＝4， 所以直线AB ：y ＝43x －43，代入抛物线方程可得，4x 2－17x ＋4＝0， 所以x 2＝14， 所以|BF |＝x 2＋1＝54. 答案：5410．在平面直角坐标系中，动点M (x ，y )(x ≥0)到点F (1,0)的距离与到y 轴的距离之差为1.(1)求点M 的轨迹C 的方程；(2)若Q (－4,2)，过点N (4,0)作任意一条直线交曲线C 于A ，B 两点，试证明k QA ＋k QB 是一个定值．解析：(1)M 到定点F (1,0)的距离与到定直线x ＝－1的距离相等， ∴M 的轨迹C 是一个开口向右的抛物线，且p ＝2， ∴M 的轨迹方程为y 2＝4x .(2)设过N (4,0)的直线的方程为x ＝my ＋4，联立方程组⎩⎪⎨⎪⎧y 2＝4x ，x ＝my ＋4整理得y 2－4my －16＝0，设直线l 与抛物线的交点为A (x 1，y 1)，B (x 2，y 2)， 则有y 1＋y 2＝4m ，y 1y 2＝－16， 又k QA ＋k QB ＝y 1－2x 1＋4＋y 2－2x 2＋4＝y 1－2my 1＋8＋y 2－2my 2＋8＝－8m 2－3216m 2＋64＝－12， 因此k QA ＋k QB 是一个定值为－12.能力提升练(时间：15分钟)11．已知直线l 1：x ＝2，l 2：3x ＋5y －30＝0，点P 为抛物线y 2＝－8x 上的任一点，则P 到直线l 1，l 2的距离之和的最小值为( )(A)2 (B)234 (C)181734(D)161534C 解析：抛物线y 2＝－8x 的焦点为F (－2,0)，准线为l 1：x ＝2. ∴P 到l 1的距离等于|PF |，∴P 到直线l 1，l 2的距离之和的最小值为F (－2,0)到直线l 2的距离d ＝|－6＋0－30|9＋25＝181734.故选C.12．已知点A (0,2)，抛物线C ：y 2＝2px (p ＞0)的焦点为F ，射线F A 与抛物线C 相交于点M ，与其准线相交于点N ，若|FM ||MN |＝55，则p 的值等于( )(A)18 (B)14 (C)2(D)4C 解析：设M (x M ，y M )，N ⎝ ⎛⎭⎪⎫－p 2，y N ，由|FM ||MN |＝55，知|FM ||FN |＝15＋1，所以y N ＝(5＋1)y M ；由k F A ＝k FN 知，y N －p ＝2－p 2，所以y N ＝4，所以y M ＝45＋1；又|FM ||FN |＝15＋1，所以p 2－x M ＝15＋1⎝ ⎛⎭⎪⎫p 2＋p 2＝p 5＋1，所以x M ＝()5－1p 2(5＋1)，将(x M ，y M )代入y 2＝2px ，得⎝ ⎛⎭⎪⎫45＋12＝2p ×(5－1)p 2(5＋1)，解得p ＝2.故选C.13．已知抛物线C ：x 2＝2py (p ＞0)的焦点为F ，O 为坐标原点，点M ⎝ ⎛⎭⎪⎫－4，p 2，N ⎝ ⎛⎭⎪⎫1，p 2，射线MO ，NO 分别交抛物线C 于异于点O 的点A ，B ，若A ，B ，F 三点共线，则p 的值为________．解析：直线OM 的方程为y ＝－p8x ，将其代入x 2＝2py ， 解方程可得⎩⎪⎨⎪⎧x ＝－p 24y ＝p 332，故A ⎝ ⎛⎭⎪⎫－p 24，p 332.直线ON 的方程为y ＝p2x ，将其代入x 2＝2py ，解方程可得⎩⎨⎧x ＝p 2y ＝p 32，故B ⎝ ⎛⎭⎪⎫p 2，p 32.又F ⎝ ⎛⎭⎪⎫0，p 2，所以k AB ＝3p 8，k BF ＝p 2－12p ，因为A ，B ，F 三点共线，所以k AB ＝k BF ，即3p 8＝p 2－12p ，解得p ＝2.答案：214．顶点在原点，经过圆C ：x 2＋y 2－2x ＋22y ＝0的圆心且准线与x 轴垂直的抛物线方程为________．解析：将圆C 的一般方程化为标准方程为(x －1)2＋(y ＋2)2＝3，圆心为(1，－2)．由题意，知抛物线的顶点在原点，焦点在x 轴上，且经过点(1，－2)．设抛物线的标准方程为y 2＝2px ，因为点(1，－2)在抛物线上，所以(－2)2＝2p ，解得p ＝1，所以所求抛物线的方程为y 2＝2x .答案：y 2＝2x15．已知AB 是抛物线x 2＝4y 的一条焦点弦，若该弦的中点纵坐标是3，则弦AB 所在的直线方程是________．解析：设A (x 1，y 1)，B (x 2，y 2)， 直线AB 的方程为x ＝m (y －1)，由抛物线的定义及题设可得，y 1＋y 2＝6， 直线与抛物线方程联立消去x 可得 m 2y 2－(2m 2＋4)y ＋m 2＝0， 则y 1＋y 2＝2m 2＋4m 2，即6＝2m 2＋4m 2， 可得m ＝1或m ＝－1.故直线方程为x －y ＋1＝0或x ＋y －1＝0. 答案：x －y ＋1＝0或x ＋y －1＝016．已知抛物线C ：y ＝mx 2(m ＞0)，焦点为F ，直线2x －y ＋2＝0交抛物线C 于A ，B 两点，P 是线段AB 的中点，过P 作x 轴的垂线交抛物线C 于点Q ，①求抛物线C 的焦点坐标．②若抛物线C 上有一点R (x R,2)到焦点F 的距离为3，求此时m 的值．③是否存在实数m ，使△ABQ 是以Q 为直角顶点的直角三角形？若存在，求出m 的值；若不存在，请说明理由．解析：①因为抛物线C ：x 2＝1m y ，所以它的焦点F (0，14m )． ②因为|RF |＝y R ＋14m ，所以2＋14m ＝3，得m ＝14.③存在，联立方程⎩⎪⎨⎪⎧y ＝mx 2，2x －y ＋2＝0，消去y 得mx 2－2x －2＝0，依题意，有Δ＝(－2)2－4×m ×(－2)＞0恒成立．解得m ＞－12.设A (x 1，mx 21)，B (x 2，mx 22)，则⎩⎪⎨⎪⎧x 1＋x 2＝2m，x 1·x 2＝－2m .(*)因为P 是线段AB 的中点，所以P ⎝ ⎛⎭⎪⎫x 1＋x 22，mx 21＋mx 222， 即P ⎝ ⎛⎭⎪⎫1m ，y P ，所以Q ⎝ ⎛⎭⎪⎫1m ，1m .得QA →＝⎝ ⎛⎭⎪⎫x 1－1m ，mx 21－1m ， QB →＝⎝⎛⎭⎪⎫x 2－1m ，mx 22－1m ， 若存在实数m ，使△ABQ 是以Q 为直角顶点的直角三角形， 则QA →·QB→＝0，即⎝ ⎛⎭⎪⎫x 1－1m ·⎝ ⎛⎭⎪⎫x 2－1m ＋⎝ ⎛⎭⎪⎫mx 21－1m ⎝ ⎛⎭⎪⎫mx 22－1m ＝0， 结合(*)化简得－4m 2－6m ＋4＝0，即2m 2－3m －2＝0， 所以m ＝2或m ＝－12.而2∈(－12，＋∞)，－12∉(－12，＋∞)．。

【答案】 ;
．（镇江市2013届高三上学期期末考试数学试题）圆心在抛物线 上,并且和抛物线的准线及 轴都相切的圆的标准方程为______.
【答案】 ;
．（江苏省泰州、南通、扬州、宿迁、淮安五市2013届高三第三次调研测试数学试卷）在平面直角坐标系 中,抛物线 上纵坐标为1的一点到焦点的距离为3,则焦点到准线的距离为______.
(1)若切线 的斜率分别为 ,求证: 为定值;
(2)求证:直线 过定点.
【答案】(1)设过 作抛物线 的切线的斜率为 ,则切线的方程为 ,
与方程 联立,消去 ,得 .
因为直线与抛物线相切,所以 ,
即 .由题意 知,此方程两根为 ,
所以 (定值)
(2)设 ,由 ,得 .
所以在 点处的切线斜率为: ,因此,切线方程为: .
化简,得
所以,动点M的轨迹C1是顶点在原点,开口向上的抛物线
法二:设M(x,y).
由 ,得 .
所以, .
由 ,得 ,即 .化简得
所以,动点M的轨迹C1是顶点在原点,开口向上的抛物线
(2)证明:由题意,得 ,⊙C2的圆心即为抛物线C1的焦点F.
设 , ,则
同理 .
设直线的方程为 .
由 得 ,即 .
所以,
【答案】
．（江苏省连云港市2013届高三上学期摸底考试（数学）（选修历史））抛物线 =4y的准线方程为___________________.
【答案】
解答题
．（苏北三市（徐州、淮安、宿迁）2013届高三第二次调研考试数学试卷）如图,已知抛物线 的焦点为 过 的直线 与抛物线 交于 两点, 为抛物线的准线与 轴的交点.
.
【答案】解:设直线方程: ,
将 代入 ,得 ,

第五十四课时 抛物线课前预习案1.掌握抛物线的定义、几何图形、标准方程及简单性质；会求抛物线的标准方程，能运用抛物线的定义、标准方程处理一些简单的实际问题。

2.熟练掌握抛物线的范围、对称性、顶点等简单几何性质，并能运用性质解决相关问题.3.能解决直线与抛物线的相交问题.1.平面内与一个定点F 和一条定直线l 的距离 的点的轨迹叫做抛物线，点F 叫做抛物线的 ，直线l 叫做抛物线的 ，定点F 定直线l 上。

3.根据抛物线的定义，可知22(0)y px p =>上一点11(,)M x y 到焦点 的距离为 。

4. 抛物线22(0)y px p =>的焦点弦（过焦点的弦）为AB ，若1122(,),(,)A x y B x y ，则有如下结论：（1）｜AB ｜＝ ；（2）12y y ＝ ；12x x ＝ 。

5. 在抛物线22(0)y px p =>中，通过焦点而垂直于x 轴的直线与抛物线两交点的坐标分别为 ，连结这两点的线段叫做 ，它的长为 。

1. 根据下列条件，写出抛物线的标准方程： （1）焦点是F （0，－3）；（2）准线方程 是x =14； （3）焦点到准线的距离是2。

2. 过点A （4，－2）的抛物线的标准方程为（ ） A ．2y x =或28x y =- B ．2y x =或28y x =C ．28y x =-D ． 28x y =-3. 抛物线214x y a=的焦点坐标为（ ） A ．1(,0)a - B ．(,0)a - C ．1(,0)aD ． (,0)a4. 抛物线214y x =上点P 的纵坐标是4，则其焦点F 到点P 的距离为（ ）A ．3B ．4C ．5D ． 65.点M 与点F （4，0）的距离比它到直线l ：x ＋5＝0的距离小1，求点M 的轨迹方程．课堂探究案考点1求抛物线的标准方程【典例1】 根据下列条件求抛物线的标准方程（1）抛物线的焦点是双曲线22169144x y -=的左顶点； （2）过点P （2，－4）；（3）抛物线的焦点在x 轴上，直线3y =-与抛物线交于点A ，||5AF =.【变式1】【2012陕西】如图是抛物线形拱桥，当水面在l 时，拱顶离水面2米，水面宽4米，水位下降1米后，水面宽 米.考点2 抛物线定义的应用【典例2】已知抛物线22y x =的焦点是F ，点P 是抛物线上的动点，点A （3，2），求 ｜PA ｜+｜PF ｜的最小值，并求出取最小值时点P 的坐标．【变式2】（1） 在22y x = 上有一点P ，它到A （2，10）的距离与它到焦点F 的距离之和最小，则P 的坐标为（ ）A ．（－2，8）B ．（2，8）C ．(2,8)--D ．（ 2，－8）（2）已知抛物线24y x =，点P 是抛物线上的动点，又有点A （6，3），｜PA ｜+｜PF ｜的最小值是__________.考点3 抛物线几何性质的应用【典例3】已知抛物线关于x 轴对称，它的顶点在坐标原点O ，并且经过点0(2,)M y .若点M 到该抛物线焦点的距离为3，则||OM =（ ）A 、、、4 D 、【变式3】已知A 、B 是抛物线22(0)y px p =>上两点，O 为坐标原点，若|OA |=|OB |，且AOB ∆的垂心恰是此抛物线的焦点，则直线AB 的方程是（ ） A.x =3pB.x =pC.x =52p D.x =32p1.已知点P 是抛物线22y x =上的一个动点，则点P 到点（0，2）的距离与P 到该抛物线准线的距离之和的最小值为（ ）A B ．3 C D ．922. 过抛物线焦点F 的直线与抛物线相交于A ，B 两点，若A ，B 在抛物线准线上的射影分别是A 1，B 1，则11A FB ∠为（ ）A ．45°B ．60°C ．90°D ．120°3.动点P 到点(2,0)F 的距离与它到直线20x +=的距离相等，则P 的轨迹方程为 ．课后拓展案组全员必做题1．（2013年四川（理））抛物线24y x =的焦点到双曲线2213yx -=的渐近线的距离是（ ）A ．12 B ．2C ．1D 2．（2011辽宁理3）已知F 是抛物线2y x =的焦点，A ，B 是该抛物线上的两点，3AF BF +=，则线段AB 的中点到y 轴的距离为( ). A ．34 B ．1 C ．54 D ．743．已知直线1:4360l x y -+=和直线2:1l x =-，抛物线24y x =上一动点P 到直线1l 和直线2l 的距离之和的最小值是( ) A.2 B.3 C.115 D.37164．（2013年课标Ⅰ（文8））O 为坐标原点,F 为抛物线2:C y =的焦点,P 为C 上一点,若||PF =,则POF ∆的面积为（ ）A ．2B ．C ．D ．4组提高选做题1．（2013山东文）抛物线)0(21:21>=p x py C 的焦点与双曲线222:13x C y -=的右焦点的连线交1C 于第一象限的点M,若1C 在点M 处的切线平行于2C 的一条渐近线,则p =（ ）A ．163B ．83 C ．332 D ．334 2．（2013年普通高等学校招生统一考试新课标Ⅱ卷数学（理）设抛物线2:2(0)C y px p =>的焦点为F ,点M 在C 上,5MF =,若以MF 为直径的圆过点)2,0(,则C 的方程为（ ） A ．24y x =或28y x = B ．22y x =或28y x = C ．24y x =或216y x = D ．22y x =或216y x =参考答案1.（1）212x y =-；（2）2y x =-；（3）24x y =，24x y =-，24y x =，24y x =-.2.A3.D4.C5. 216y x =【典例1】（1）212y x =-；（2）28y x =或2x y =-；（3）x y 22±=或x y 182±=【变式1】【典例2】最小值为72；(2,2)P . 【变式2】（1）B ；（2）7. 【典例3】B【变式3】C1.A2.C3. 28y x组全员必做题1.B2.C3.A4.C组提高选做题1.D2.C。

解：设 A(x1，y1)，B(x2，y2)，由yy2＝＝k8xx，＋2， 得 k2x2＋(4k2－8)x＋4k2＝0，所以 x1＋x2＝k82－4， x1x2＝4. 又由抛物线的定义可知|FA|＝x1＋2，|FB|＝x2＋2， 所以 x1＋2＝2(x2＋2)，即 x1＝2(x2＋1)，代入 x1x2＝4 得 2(x2＋1)x2＝4，解得 x2＝1(x2＝－2 舍去)， 将 x2＝1，x1＝4 代入 x1＋x1＝k82－4 得 k2＝89，由已知 k>0， 所以 k＝232.
第30页/共41页
3．在解决以圆锥曲线为背景的创新交汇问题时，应 注意以下两点
(1)注意解实际应用问题的四个解题步骤，同时对有 关圆锥曲线的基本知识必须要熟练掌握，以便能及时提 取运用．
(2)注意观察实际生活中一些形状与圆锥曲线的形状 接近的事物，如截面为抛物线形的拱桥、探照灯，截面 为双曲线形的烟筒，斜截圆柱得椭圆形状的截面等．
第25页/共41页
4 个结论——直线与抛物线相交的四个结论
已知抛物线y2＝2px(p>0)，过其焦点的直线交抛物线 于A，B两点，设A(x1，y1)，B(x2，y2)，则有以下结论：
(1)|AB|＝x1＋x2＋p 或|AB|＝si2np2α(α 为 AB 所在直线的 倾斜角)；
(2)x1x2＝p42； (3)y1y2＝－p2； (4)过抛物线焦点且与对称轴垂直的弦称为抛物线的 通径，抛物线的通径长为2p.
第16页/共41页
抛物线的标准方程与性质 [例2] (1)抛物线y2＝24ax(a>0)上有一点M，它的横 坐标是3，它到焦点的距离是5，则抛物线的方程为____. (2)设抛物线y2＝2px(p>0)的焦点为F，点A(0,2)．若 线段FA的中点B在抛物线上，则B到该抛物线准线的距离 为________．

江苏省响水中学2014届高考数学一轮复习 第43-44课时 抛物线学案文新人教A 版一、复习目标：1、了解并重视抛物线定义在解题中的应用，掌握抛物线标准方程的四种形式， 能用待定系数法求抛物线标准方程。

2、掌握抛物线的标准方程和几何性质，会用抛物线的标准方程和几何性质解决简单的实际问题。

二、知识梳理：1、定义：2、标准方程：3、几何性质：4、焦点弦长：过抛物线22y px =(0)p >焦点F 的弦AB ，若1122(,),(,)A x y B x y ，则||AF = ，||AB = ，12x x = ，12y y = ．5、抛物线22x py =(0)p >的焦点为F ，AB 是过焦点F 且倾斜角为α的弦，若1122(,),(,)A x y B x y ，则12x x = ；12y y = ；||AB = ．三、基础训练：1、（1）抛物线24y x =的焦点坐标为______________（2）设抛物线的顶点在原点，准线方程为2x =-，则抛物线的方程是2、已知直线l 过抛物线C 的焦点,且与C 的对称轴垂直,l 与C 交于A,B 两点,|AB|=12, P 为C 的准线上一点,则ABP ∆的面积为________.3、经过点(4,2)P -的抛物线的标准方程为_________________4、若AB 为经过抛物线24y x =焦点的弦，且4AB =，O 为坐标原点， 则AOB ∆的面积等于_____________5、 已知以F 为焦点的抛物线y 2＝4x 上的两点A 、B 满足AF →＝3FB →，则弦AB 的中点到准线的距离为__________．6、对于顶点在原点的抛物线，给出下列条件：①焦点在y 轴上；②焦点在x 轴上；③抛物线上横坐标为1的点到焦点的距离等于6；④抛物线的通径的长为5；⑤由原点向过焦点的某条直线作垂线，垂足坐标为（2，1）.能使这抛物线方程为y 2=10x 的条件是____________.（要求填写合适条件的序号）7、将两个顶点在抛物线22(0)y px p =>上，另一个顶点是此抛物线焦点的正三角形个数记为n ，则_______8、已知直线1l ：4360x y -+=和直线2l ：1x =-，抛物线24y x =上一动点P 到直线1l 和直线2l 的距离之和的最小值为 。

学案53 抛物线导学目标： 1.掌握抛物线的定义、几何图形和标准方程，知道它们的简单几何性质.2.理解数形结合的思想．自主梳理1．抛物线的概念平面内与一个定点F 和一条定直线l (F ∉l )距离______的点的轨迹叫做抛物线．点F 叫做抛物线的__________，直线l 叫做抛物线的________．2自我检测 1．(2010·四川)抛物线y 2＝8x 的焦点到准线的距离是( ) A ．1 B ．2 C ．4 D ．82．若抛物线y 2＝2px 的焦点与椭圆x 26＋y22＝1的右焦点重合，则p 的值为( )A ．－2B ．2C ．－4D ．4 3．(2011·陕西)设抛物线的顶点在原点，准线方程为x ＝－2，则抛物线的方程是( )A ．y 2＝－8x B ．y 2＝8x C ．y 2＝－4x D ．y 2＝4x4．已知抛物线y 2＝2px (p >0)的焦点为F ，点P 1(x 1，y 1)，P 2(x 2，y 2)，P 3(x 3，y 3)在抛物线上，且2x 2＝x 1＋x 3，则有( )A ．|FP 1|＋|FP 2|＝|FP 3|B ．|FP 1|2＋|FP 2|2＝|FP 3|2C ．2|FP 2|＝|FP 1|＋|FP 3|D ．|FP 2|2＝|FP 1|·|FP 3| 5．(2011·佛山模拟)已知抛物线方程为y 2＝2px (p >0)，过该抛物线焦点F 且不与x 轴垂直的直线AB 交抛物线于A 、B 两点，过点A 、点B 分别作AM 、BN 垂直于抛物线的准线，分别交准线于M 、N 两点，那么∠MFN 必是( )A ．锐角B ．直角C ．钝角D ．以上皆有可能探究点一 抛物线的定义及应用例1 已知抛物线y 2＝2x 的焦点是F ，点P 是抛物线上的动点，又有点A (3,2)，求|P A |＋|PF |的最小值，并求出取最小值时P 点的坐标．变式迁移1 已知点P 在抛物线y 2＝4x 上，那么点P 到点Q (2，－1)的距离与点P 到抛物线焦点距离之和取得最小值时，点P 的坐标为( )A.⎝⎛⎭⎫14，－1B.⎝⎛⎭⎫14，1 C ．(1,2) D ．(1，－2) 探究点二 求抛物线的标准方程 例2 (2011·芜湖调研)已知抛物线的顶点在原点，焦点在y 轴上，抛物线上一点M (m ，－3)到焦点的距离为5，求m 的值、抛物线方程和准线方程．变式迁移2 根据下列条件求抛物线的标准方程：(1)抛物线的焦点F 是双曲线16x 2－9y 2＝144的左顶点； (2)过点P (2，－4)．探究点三 抛物线的几何性质例3 过抛物线y 2＝2px 的焦点F 的直线和抛物线相交于A ，B 两点，如图所示．(1)若A ，B 的纵坐标分别为y 1，y 2，求证：y 1y 2＝－p 2；(2)若直线AO 与抛物线的准线相交于点C ，求证：BC ∥x 轴．变式迁移3 已知AB 是抛物线y 2＝2px (p >0)的焦点弦，F 为抛物线的焦点，A (x 1，y 1)，B (x 2，y 2)．求证：(1)x 1x 2＝p 24；(2)1|AF |＋1|BF |为定值．分类讨论思想的应用例 (12分)过抛物线y 2＝2px (p >0)焦点F 的直线交抛物线于A 、B 两点，过B 点作其准线的垂线，垂足为D ，设O 为坐标原点，问：是否存在实数λ，使AO →＝λOD →？多角度审题 这是一道探索存在性问题，应先假设存在，设出A 、B 两点坐标，从而得到D 点坐标，再设出直线AB 的方程，利用方程组和向量条件求出λ.【答题模板】解 假设存在实数λ，使AO →＝λOD →. 抛物线方程为y 2＝2px (p >0)，则F ⎝⎛⎭⎫p 2，0，准线l ：x ＝－p 2， (1)当直线AB 的斜率不存在，即AB ⊥x 轴时，交点A 、B 坐标不妨设为：A ⎝⎛⎭⎫p 2，p ，B ⎝⎛⎭⎫p2，－p . ∵BD ⊥l ，∴D ⎝⎛⎭⎫－p2，－p ， ∴AO →＝⎝⎛⎭⎫－p 2，－p ，OD →＝⎝⎛⎭⎫－p 2，－p ，∴存在λ＝1使AO →＝λOD →.[4分] (2)当直线AB 的斜率存在时，设直线AB 的方程为y ＝k ⎝⎛⎭⎫x －p2 (k ≠0)，设A (x 1，y 1)，B (x 2，y 2)，则D ⎝⎛⎭⎫－p 2，y 2，x 1＝y 212p ，x 2＝y 222p， 由⎩⎪⎨⎪⎧y ＝k ⎝⎛⎭⎫x －p 2y 2＝2px得ky 2－2py －kp 2＝0，∴y 1y 2＝－p 2，∴y 2＝－p 2y 1，[8分]AO →＝(－x 1，－y 1)＝⎝⎛⎭⎫－y 212p ，－y 1，OD →＝⎝⎛⎭⎫－p 2，y 2＝⎝⎛⎭⎫－p 2，－p 2y 1，假设存在实数λ，使AO →＝λOD →，则⎩⎨⎧－y 212p ＝－p 2λ－y 1＝－p 2y1λ，解得λ＝y 21p 2，∴存在实数λ＝y 21p2，使AO →＝λOD →.综上所述，存在实数λ，使AO →＝λOD →.[12分] 【突破思维障碍】由抛物线方程得其焦点坐标和准线方程，按斜率存在和不存在讨论，由直线方程和抛物线方程组成方程组，研究A 、D 两点坐标关系，求出AO →和OD →的坐标，判断λ是否存在．【易错点剖析】解答本题易漏掉讨论直线AB 的斜率不存在的情况，出现错误的原因是对直线的点斜式方程认识不足．4(满分：75分)一、选择题(每小题5分，共25分) 1．(2011·大纲全国)已知抛物线C ：y 2＝4x 的焦点为F ，直线y ＝2x －4与C 交于A ，B 两点，则cos ∠AFB 等于( )A.45B.35C ．－35D ．－452．(2011·湖北)将两个顶点在抛物线y 2＝2px (p >0)上，另一个顶点是此抛物线焦点的正三角形个数记为n ，则( )A ．n ＝0B ．n ＝1C ．n ＝2D ．n ≥33．已知抛物线y 2＝2px ，以过焦点的弦为直径的圆与抛物线准线的位置关系是( ) A ．相离 B ．相交 C ．相切 D ．不确定 4．(2011·泉州月考)已知点A (－2,1)，y 2＝－4x 的焦点是F ，P 是y 2＝－4x 上的点，为使|P A |＋|PF |取得最小值，则P 点的坐标是( )A.⎝⎛⎭⎫－14，1 B ．(－2,22) C.⎝⎛⎭⎫－14，－1 D ． (－2，－22) 5．设O 为坐标原点，F 为抛物线y 2＝4x 的焦点，A 为抛物线上一点，若OA →·AF →＝－4，则点A 的坐标为( )A ．(2，±2)B ．(1，±2)C ．(1,2)D ．(2，2) 二、填空题(每小题4分，共12分) 6．(2011·重庆)设圆C 位于抛物线y 2＝2x 与直线x ＝3所围成的封闭区域(包含边界)内，则圆C 的半径能取到的最大值为________．7．(2011·济宁期末)已知A 、B 是抛物线x 2＝4y 上的两点，线段AB 的中点为M (2,2)，则|AB |＝________.8．(2010·浙江)设抛物线y 2＝2px (p >0)的焦点为F ，点A (0，2)．若线段F A 的中点B 在抛物线上，则B 到该抛物线准线的距离为________．三、解答题(共38分) 9．(12分)已知顶点在原点，焦点在x 轴上的抛物线截直线y ＝2x ＋1所得的弦长为15，求抛物线方程．10．(12分)(2011·韶关模拟)已知抛物线C ：x 2＝8y .AB 是抛物线C 的动弦，且AB 过F (0,2)，分别以A 、B 为切点作轨迹C 的切线，设两切线交点为Q ，证明：AQ ⊥BQ .11．(14分)(2011·济南模拟)已知定点F (0,1)和直线l 1：y ＝－1，过定点F 与直线l 1相切的动圆圆心为点C .(1)求动点C 的轨迹方程；(2)过点F 的直线l 2交轨迹C 于两点P 、Q ，交直线l 1于点R ，求RP →·RQ →的最小值．学案53 抛物线自主梳理1．相等 焦点 准线 自我检测 1．C2．B [因为抛物线的准线方程为x ＝－2，所以p2＝2，所以p ＝4，所以抛物线的方程是y 2＝8x .所以选B.]3．B 4.C 5.B 课堂活动区例1 解题导引 重视定义在解题中的应用，灵活地进行抛物线上的点到焦点的距离与到准线距离的等价转化，是解决抛物线焦点弦有关问题的重要途径．解将x ＝3代入抛物线方程 y 2＝2x ，得y ＝±6.∵6>2，∴A 在抛物线内部． 设抛物线上点P 到准线l ：x ＝－12的距离为d ，由定义知|P A |＋|PF |＝|P A |＋d ，当P A ⊥l 时，|P A |＋d 最小，最小值为72，即|P A |＋|PF |的最小值为72，此时P 点纵坐标为2，代入y 2＝2x ，得x ＝2， ∴点P 坐标为(2,2)． 变式迁移1 A [点P 到抛物线焦点的距离等于点P 到抛物线准线的距离，如图，|PF |＋|PQ |＝|PS |＋|PQ |，故最小值在S ，P ，Q 三点共线时取得，此时P ，Q 的纵坐标都是－1，点P 的坐标为⎝⎛⎭⎫14，－1.] 例2 解题导引 (1)求抛物线方程时，若由已知条件可知所求曲线是抛物线，一般用待定系数法．若由已知条件可知所求曲线的动点的轨迹，一般用轨迹法；(2)待定系数法求抛物线方程时既要定位(即确定抛物线开口方向)，又要定量(即确定参数p 的值)．解题关键是定位，最好结合图形确定方程适合哪种形式，避免漏解；(3)解决抛物线相关问题时，要善于用定义解题，即把|PF |转化为点P 到准线的距离，这种“化斜为直”的转化方法非常有效，要注意领会和运用．解 方法一 设抛物线方程为 x 2＝－2py (p >0)，则焦点为F ⎝⎛⎭⎫0，－p 2，准线方程为y ＝p 2. ∵M (m ，－3)在抛物线上，且|MF |＝5，∴⎩⎪⎨⎪⎧m 2＝6p ， m 2＋⎝⎛⎭⎫－3＋p 22＝5， 解得⎩⎨⎧p ＝4，m ＝±2 6. ∴抛物线方程为x 2＝－8y ，m ＝±26， 准线方程为y ＝2. 方法二 如图所示，设抛物线方程为x 2＝－2py (p >0)，则焦点F ⎝⎛⎭⎫0，－p 2， 准线l ：y ＝p2，作MN ⊥l ，垂足为N .则|MN |＝|MF |＝5，而|MN |＝3＋p2，∴3＋p2＝5，∴p ＝4.∴抛物线方程为x 2＝－8y ，准线方程为y ＝2.由m 2＝(－8)×(－3)，得m ＝±2 6.变式迁移2 解 (1)双曲线方程化为x 29－y216＝1，左顶点为(－3,0)，由题意设抛物线方程为y 2＝－2px (p >0)且－p2＝－3，∴p ＝6.∴方程为y 2＝－12x .(2)由于P (2，－4)在第四象限且对称轴为坐标轴，可设方程为y 2＝mx (m >0)或x 2＝ny (n <0)，代入P 点坐标求得m ＝8，n ＝－1，∴所求抛物线方程为y 2＝8x 或x 2＝－y .例3 解题导引 解决焦点弦问题时，抛物线的定义有着广泛的应用，而且还应注意焦点弦的几何性质．焦点弦有以下重要性质(AB 为焦点弦，以y 2＝2px (p >0)为例)：①y 1y 2＝－p 2，x 1x 2＝p 24；②|AB |＝x 1＋x 2＋p .证明 (1)方法一 由抛物线的方程可得焦点坐标为F ⎝⎛⎭⎫p 2，0.设过焦点F 的直线交抛物线于A ，B 两点的坐标分别为(x 1，y 1)、(x 2，y 2)．①当斜率存在时，过焦点的直线方程可设为y ＝k ⎝⎛⎭⎫x －p 2，由⎩⎪⎨⎪⎧y ＝k ⎝⎛⎭⎫x －p 2，y 2＝2px ，消去x ，得ky 2－2py －kp 2＝0.(*)当k ＝0时，方程(*)只有一解，∴k ≠0， 由韦达定理，得y 1y 2＝－p 2；②当斜率不存在时，得两交点坐标为 ⎝⎛⎭⎫p 2，p ，⎝⎛⎭⎫p 2，－p ，∴y 1y 2＝－p 2. 综合两种情况，总有y 1y 2＝－p 2.方法二 由抛物线方程可得焦点F ⎝⎛⎭⎫p 2，0，设直线AB 的方程为x ＝ky ＋p2，并设A (x 1，y 1)，B (x 2，y 2)，则A 、B 坐标满足⎩⎪⎨⎪⎧x ＝ky ＋p 2，y 2＝2px ，消去x ，可得y 2＝2p ⎝⎛⎭⎫ky ＋p 2， 整理，得y 2－2pky －p 2＝0，∴y 1y 2＝－p 2. (2)直线AC 的方程为y ＝y 1x 1x ，∴点C 坐标为⎝⎛⎭⎫－p 2，－py 12x 1，y C ＝－py 12x 1＝－p 2y 12px 1.∵点A (x 1，y 1)在抛物线上，∴y 21＝2px 1.又由(1)知，y 1y 2＝－p 2，∴y C ＝y 1y 2·y 1y 21＝y 2，∴BC ∥x 轴．变式迁移3 证明 (1)∵y 2＝2px (p >0)的焦点F ⎝⎛⎭⎫p 2，0，设直线方程为y ＝k ⎝⎛⎭⎫x －p 2 (k ≠0)，由⎩⎪⎨⎪⎧y ＝k ⎝⎛⎭⎫x －p 2y 2＝2px，消去x ，得ky 2－2py －kp 2＝0. ∴y 1y 2＝－p 2，x 1x 2＝(y 1y 2)24p 2＝p 24，当k 不存在时，直线方程为x ＝p 2，这时x 1x 2＝p 24.因此，x 1x 2＝p24恒成立．(2)1|AF |＋1|BF |＝1x 1＋p 2＋1x 2＋p2＝x 1＋x 2＋px 1x 2＋p 2(x 1＋x 2)＋p 24.又∵x 1x 2＝p 24，代入上式得1|AF |＋1|BF |＝2p ＝常数，所以1|AF |＋1|BF |为定值．课后练习区1．D [方法一 由⎩⎪⎨⎪⎧ y ＝2x －4，y 2＝4x ，得⎩⎪⎨⎪⎧ x ＝1，y ＝－2或⎩⎪⎨⎪⎧x ＝4，y ＝4. 令B (1，－2)，A (4,4)，又F (1,0)，∴由两点间距离公式得|BF |＝2，|AF |＝5，|AB |＝3 5.∴cos ∠AFB ＝|BF |2＋|AF |2－|AB |22|BF |·|AF |＝4＋25－452×2×5＝－45.方法二 由方法一得A (4,4)，B (1，－2)，F (1,0)， ∴F A →＝(3,4)，FB →＝(0，－2)， ∴|F A →|＝32＋42＝5，|FB →|＝2.∴cos ∠AFB ＝F A →·FB →|F A →|·|FB →|＝3×0＋4×(－2)5×2＝－45.]2．C [如图所示，A ，B 两点关于x 轴对称，F 点坐标为(p2，0)，设A (m ，2pm )(m >0)，则由抛物线定义，|AF |＝|AA 1|，即m ＋p2＝|AF |.又|AF |＝|AB |＝22pm ，∴m ＋p 2＝22pm ，整理，得m 2－7pm ＋p 24＝0，①∴Δ＝(－7p )2－4×p24＝48p 2>0，∴方程①有两相异实根，记为m 1，m 2，且m 1＋m 2＝7p >0，m 1·m 2＝p 24>0，∴m 1>0，m 2>0，∴n ＝2.] 3．C4．A [过P 作PK ⊥l (l 为抛物线的准线)于K ，则|PF |＝|PK |， ∴|P A |＋|PF |＝|P A |＋|PK |.∴当P 点的纵坐标与A 点的纵坐标相同时，|P A |＋|PK |最小，此时P 点的纵坐标为1，把y ＝1代入y 2＝－4x ，得x ＝－14，即当P 点的坐标为⎝⎛⎭⎫－14，1时，|P A |＋|PF |最小．] 5．B 6.6－1解析 如图所示，若圆C 的半径取到最大值，需圆与抛物线及直线x ＝3同时相切，设圆心的坐标为(a,0)(a <3)，则圆的方程为(x －a )2＋y 2＝(3－a )2，与抛物线方程y 2＝2x 联立得x 2＋(2－2a )x ＋6a －9＝0，由判别式Δ＝(2－2a )2－4(6a －9)＝0，得a ＝4－6，故此时半径为3－(4－6)＝6－1.7．4 2解析 由题意可设AB 的方程为y ＝kx ＋m ，与抛物线方程联立得x 2－4kx －4m ＝0，线段AB 中点坐标为(2,2)，x 1＋x 2＝4k ＝4，得k ＝1.又∵y 1＋y 2＝k (x 1＋x 2)＋2m ＝4，∴m ＝0.从而直线AB ：y ＝x ，|AB |＝2|OM |＝4 2. 8.324解析 抛物线的焦点F 的坐标为⎝⎛⎭⎫p 2，0，线段F A 的中点B 的坐标为⎝⎛⎭⎫p4，1，代入抛物线方程得1＝2p ×p 4，解得p ＝2，故点B 的坐标为⎝⎛⎭⎫24，1，故点B 到该抛物线准线的距离为24＋22＝324. 9．解 设直线和抛物线交于点A (x 1，y 1)，B (x 2，y 2)，(1)当抛物线开口向右时，设抛物线方程为y 2＝2px (p >0)，则⎩⎪⎨⎪⎧y 2＝2px y ＝2x ＋1，消去y 得，4x 2－(2p －4)x ＋1＝0，∴x 1＋x 2＝p －22，x 1x 2＝14，(4分)∴|AB |＝1＋k 2|x 1－x 2| ＝5·(x 1＋x 2)2－4x 1x 2＝5·⎝⎛⎭⎫p －222－4×14＝15，(7分)则 p 24－p ＝3，p 2－4p －12＝0，解得p ＝6(p ＝－2舍去)，抛物线方程为y 2＝12x .(9分)(2)当抛物线开口向左时，设抛物线方程为y 2＝－2px (p >0)，仿(1)不难求出p ＝2， 此时抛物线方程为y 2＝－4x .(11分) 综上可得，所求的抛物线方程为y 2＝－4x 或y 2＝12x .(12分) 10．证明 因为直线AB 与x 轴不垂直，设直线AB 的方程为y ＝kx ＋2，A (x 1，y 1)，B (x 2，y 2)．由⎩⎪⎨⎪⎧y ＝kx ＋2，y ＝18x 2，可得x 2－8kx －16＝0，x 1＋x 2＝8k ，x 1x 2＝－16.(4分)抛物线方程为y ＝18x 2，求导得y ′＝14x .(7分)所以过抛物线上A 、B 两点的切线斜率分别是k 1＝14x 1，k 2＝14x 2，k 1k 2＝14x 1·14x 2 ＝116x 1·x 2＝－1.(10分) 所以AQ ⊥BQ .(12分)11．解 (1)由题设点C 到点F 的距离等于它到l 1的距离，所以点C 的轨迹是以F 为焦点，l 1为准线的抛物线，∴所求轨迹的方程为x 2＝4y .(5分)(2)由题意直线l 2的方程为y ＝kx ＋1，与抛物线方程联立消去y 得x 2－4kx －4＝0. 记P (x 1，y 1)，Q (x 2，y 2)，则x 1＋x 2＝4k ，x 1x 2＝－4.(8分)因为直线PQ 的斜率k ≠0，易得点R 的坐标为⎝⎛⎭⎫－2k ，－1.(9分) RP →·RQ →＝⎝⎛⎭⎫x 1＋2k ，y 1＋1·⎝⎛⎭⎫x 2＋2k ，y 2＋1 ＝⎝⎛⎭⎫x 1＋2k ⎝⎛⎭⎫x 2＋2k ＋(kx 1＋2)(kx 2＋2) ＝(1＋k 2)x 1x 2＋⎝⎛⎭⎫2k ＋2k (x 1＋x 2)＋4k2＋4 ＝－4(1＋k 2)＋4k ⎝⎛⎭⎫2k ＋2k ＋4k2＋4 ＝4⎝⎛⎭⎫k 2＋1k 2＋8，(11分) ∵k 2＋1k2≥2，当且仅当k 2＝1时取到等号． RP →·RQ →≥4×2＋8＝16，即RP →·RQ →的最小值为16. (14分)。

9.7抛物线考情分析抛物线的定义、标准方程、几何性质，以及直线与抛物线的位置关系等是高考热点，题型既有选择填空题，又有解答题；客观题突出“小而巧”主要考查抛物线的定义、标准方程，主观题除考查定义、性质外，还考查直线与抛物线的位置关系，考查基本运算能力及逻辑推理能力。

基础知识1、抛物线的定义：平面内一个定点F 与一条定直线l （F l ∉）的距离相等的轨迹叫做抛物线，点F 叫做抛物线的焦点，直线l 叫做抛物线的准线。

2、抛物线的标准方程与几何意义：标准方程22y px=（0p >）22y px =-22x py =（0p >）22x py =-（0p >）图形范围 x ≥0，y R ∈ x ≤0，y R ∈ y ≥0，x R ∈y ≤0，x R ∈焦点 ,02p ⎛⎫ ⎪⎝⎭,02p ⎛⎫- ⎪⎝⎭0,2p ⎛⎫ ⎪⎝⎭0,2p ⎛⎫- ⎪⎝⎭准线 2px =-2p x =2p y =-2p y =焦半径 02p PF x =+ 02p PF x =-+ 02p PF y =+ 02p PF y =-+对称轴 x 轴y 轴顶点 ()0,0离心率1e =3、焦点弦的性质： 焦点弦： 过px y22=()0>p 的焦点的弦ＡＢ。

Ａ（1x ，1y ）Ｂ（2x ，2y ）FFO FF（1）12AB x x p =++（2）221p y y -=，4221p x x =，（3）以AB 为直径的圆与准线相切（4）抛物线的通径：通过焦点并且垂直于对称轴的直线与抛物线两交点之间的线段叫做抛物线的通径.通径的长为2p ,通径是过焦点最短的弦. 4、直线与抛物线的位置关系：（1）将直线方程与抛物线方程联立消去y （或消去x ）得：20ax bx c ++=或20ay by c ++=（1）0a =或⇔>∆0相交；（2）⇔=∆0相切；（3）⇔<∆0相离直线与抛物线只有一个公共点：相交或相切。

由题悟法 涉及抛物线上的点到焦点 (准线 )的距离问题，可优先考虑利用抛物线的定义转化为点到 准线 (焦点 )的距离问题求解．
以题试法 1． (2012 安·徽高考 )过抛物线 y2＝ 4x 的焦点 F 的直线交该抛物线于 ＝3，则 |BF|＝ ________.
A，B 两点．若 |AF |
解析： 由题意知，抛物线的焦点 F 的坐标为 (1,0) ，又∵ |AF |＝ 3，
义知
|PF
|＝
xP
＋p＝ 2
6.
答案： 6
p 1.抛物线方程中，字母 p 的几何意义是抛物线的焦点 F 到准线的距离， 2等于焦点到抛
物线顶点的距离，记牢对解题非常有帮助．
2．用抛物线定义解决问题，体现了等价转换思想的应用． 3．由 y2＝ mx( m≠ 0)或 x2＝ my(m≠ 0)求焦点坐标时，只需将 定焦点位置即可．
＝( y1＋ 1)＋ (y2＋ 1)＝ (y1＋ y2)＋ 2＝ 16. 4．(2012 郑·州模拟 )已知斜率为 2 的直线 l 过抛物线 y2＝ ax(a＞ 0)的焦点 F ，且与 y 轴相
交于点 A，若△ OAF( O 为坐标原点 )的面积为 4，则抛物线方程为 ________．
解析： 依题意得， |OF |＝ a4，又直线 l 的斜率为 2，可知 |AO|＝ 2|OF|＝ a2，△ AOF 的面积
由抛物线定义知， 点 A 到准线 x＝－ 1 的距离为 3，∴点 A 的横坐标为
2. 将 x＝ 2 代入 y2＝ 4x 得 y2＝8，由图知， y＝ 2 2，
∴ A(2,2 2)，∴直线 AF 的方程为 y＝ 2 2(x－ 1)．
y＝2 2 x－1 ， 又 y2＝ 4x，
解得

2014届高考数学(重庆专用理科)一轮复习教学案9.7抛物线
9.7抛物线
考大纲求
1．掌握抛物线的定义、几何图形和标准方程，知道其简单的几何性质(范围、对称性、极点、离心率 )．
2．理解数形联合的思想．
3．认识抛物线的简单应用，认识抛物线的实质背景，认识抛物线在刻画现实世界和解
决实质问题中的作用．
1．抛物线的定义
平面内与一个定点 F 和一条定直线l( F?l )的距离 ____ 的点的轨迹叫做抛物线．点F叫做抛物线的 ____，直线 l 叫做抛物线的 ____ ．
2．抛物线的标准方程与几何性质
标准y2＝2px y2＝－ 2px x2＝ 2py x2＝－ 2py (p＞ 0)(p＞ 0)(p＞ 0)( p＞0)
方程
p 的几何意义：焦点 F 到准线 l 的距离。

江苏省盐城市时杨中学2014届高考数学一轮复习 抛物线导学案 【学习目标】1、 了解抛物线的标准方程，会求抛物线的标准方程；2、 了解抛物线的简单几何性质。

【问题情境】一、知识回顾：二、预习练习：1、抛物线21x my =的焦点坐标为 。

2、过抛物线x y 42=的焦点作直线交抛物线于),(11y x A ,),(22y x B 两点，若621=+x x ，则=||AB 。

3、已知抛物线x y 42=的焦点为F ，抛物线上有一点M 。

(1)定点)2,4(-P ，若要使得MP MF +最小，则M 点坐标为 。

(2) 定点)5,4(Q ,动点M 的横坐标为0x ,则MQ x +0的最小值为 。

4、 过抛物线2ax y =焦点F 的一条动弦PQ ，若m PF =||,n QF =||,则nm 11+等于_______________。

【我的疑问】备 注第1页共4页例1已知抛物线顶点在原点，焦点在坐标轴上，又知此抛物线上一点)3,(-m A 到焦第2页共4页【课堂检测】1、直线l 过抛物线ax y =2的焦点且与x 轴垂直,若l 被抛物线截得的线段长为4,则正数=a 。

2、过点(0, 2)与抛物线x y 82=只有一个公共点的直线有 条。

3、一动点到y 轴距离比到点(2, 0)的距离小2,则此动点的轨迹方程为 。

4、以椭圆1162522=+y x 的中心为顶点,以椭圆的左准线为准线的抛物线与椭圆右准线交B A 、于两点,则=AB 。

5、以抛物线)0(22>=p px y 过焦点的一条弦AB 为直径的圆与准线相切于点)3,2(--C 。

（1）求这个圆的方程； （2）求AOB ∆的面积。

【回标反馈】备 注第3页共4页【巩固练习】1、已知抛物线方程为28y x =，则它的焦点坐标是 ，准线方程是 ，若该抛物线上一点到y 轴的距离等于5，则它到抛物线的焦点的距离等于 ，抛物线上的点M 到焦点的距离是4，则点M 的坐标是 。

【训练1】 (2012· 启东模拟)已知点P是抛物线y2＝2x上的一个 动点，则点P到点(0,2)的距离与点P到该抛物线准线的距 离之和的最小值为________．
解析 由抛物线的定义知，点 P 到该抛物线准线的距离等于
点 P 到其焦点的距离， 因此点 P 到点(0,2)的距离与点 P 到该 抛物线准线的距离之和即为点 P 到点(0,2)的距离与点 P 到焦 点的距离之和，显然，当 P、F、(0,2)三点共线时，距离之和 取得最小值，最小值等于
一个复习指导 本节内容是每年高考的必考内容，主要考查抛物线的定义、 标准方程与几何性质或求轨迹问题、直线与抛物线的综合
问题．填空题主要考查抛物线的性质，解答题则重点考查
解析几何的思想方法以及数形结合的思想，函数与方程的 思想，分类讨论的思想等题型．
考点自测
1．已知抛物线的焦点坐标是(0，－3)，则抛物线的标准 方程是________．
(2)由条件得抛物线 C 的方程为 x2＝8y， 则 F(0,2)，x2＝8y2，准线 l 方程为 y＝－2. 0 0 由题意，得 4<FM＝y0＋2，所以 y0>2. 故 y0 的取值范围是(2，＋∞)．
考向三
【例 3】
抛物线的综合应用
(2012· 盐城调研)如图， 已知抛物线 C：
y2＝2px(p>0)的准线为 l，焦点为 F.⊙M 的圆 心在 x 轴的正半轴上，且与 y 轴相切．过原 π 点 O 作倾斜角为 的直线 n，交 l 于点 A，交 3 ⊙M 于另一点 B，且 AO＝OB＝2. (1)求⊙M 和抛物线 C 的方程；
→ → (2)若 P 为抛物线 C 上的动点，求PM· 的最小值； PF (3)过 l 上的动点 Q 向⊙M 作切线，切点为 S，T，求证：直 线 ST 恒过一个定点，并求该定点的坐标．

8.7抛_物_线1．抛物线的定义满足以下三个条件的点的轨迹是抛物线： (1)在平面内；(2)动点到定点F 距离与到定直线l 的距离相等； (3)定点不在定直线上．2．抛物线的标准方程和几何性质 标准方程y 2＝2px (p ＞0)y 2＝－2px (p ＞0)x 2＝2py (p >0)x 2＝－2py (p >0)p 的几何意义：焦点F 到准线l 的距离图形顶点 O (0,0)对称轴 y ＝0x ＝0焦点 F (p2，0) F (－p2，0)F (0，p 2)F (0，－p2)离心率 e ＝1准线 方程 x ＝－p 2x ＝p 2 y ＝－p 2y ＝p 2 范围 x ≥0，y ∈R x ≤0，y ∈R y ≥0，x ∈R y ≤0，x ∈R 开口方向 向右 向左 向上 向下 焦半径(其中P (x 0，y 0)|PF |＝x 0＋p2|PF |＝－x 0＋p2|PF |＝y 0＋p2|PF |＝－y 0＋p21．抛物线的定义中易忽视“定点不在定直线上”这一条件，当定点在定直线上时，动点的轨迹是过定点且与直线垂直的直线．2．抛物线标准方程中参数p 易忽视只有p ＞0，才能证明其几何意义是焦点F 到准线l 的距离，否则无几何意义．『试一试』1．抛物线y 2＝8x 的焦点到准线的距离是________．『解析』抛物线y 2＝8x 的焦点为(2,0)，准线方程为x ＝－2，所以焦点到准线的距离为4.『答案』42．动圆过点(1,0)，且与直线x ＝－1相切，则动圆的圆心的轨迹方程为________． 『解析』设动圆的圆心坐标为(x ，y )，则圆心到点(1,0)的距离与到直线x ＝－1的距离相等，根据抛物线的定义易知动圆的圆心的轨迹方程为y 2＝4x .『答案』y 2＝4x1．转化思想在定义中应用抛物线上点到焦点距离常用定义转化为点到准线的距离． 2．与焦点弦有关的常用结论 (以下图为依据)(1)y 1y 2＝－p 2，x 1x 2＝p 24. (2)|AB |＝x 1＋x 2＋p ＝2psin 2θ(θ为AB 的倾斜角)．(3)1|AF |＋1|BF |为定值2p. (4)以AB 为直径的圆与准线相切． (5)以AF 或BF 为直径的圆与y 轴相切． 『练一练』1．若抛物线x 2＝ay 过点A ⎝⎛⎭⎫1，14，则点A 到此抛物线的焦点的距离为________． 『解析』由题意可知，点A 在抛物线x 2＝ay 上，所以1＝14a ，解得a ＝4，得x 2＝4y .由抛物线的定义可知点A 到焦点的距离等于点A 到准线的距离，所以点A 到抛物线的焦点的距离为y A ＋44＝14＋1＝54.『答案』542．已知过抛物线y 2＝4x 的焦点F 的直线交该抛物线于A ，B 两点，O 是坐标原点，|AF |＝2，则|BF |＝________，△OAB 的面积是________．『解析』设A (x 0，y 0)，由抛物线定义知x 0＋1＝2， ∴x 0＝1，则直线AB ⊥x 轴， ∴|BF |＝|AF |＝2，|AB |＝4.故△OAB 的面积S ＝12|AB ||OF |＝12×4×1＝2.『答案』2 2考点一抛物线的标准方程及几何性质1.(2013·南通、扬州、泰州二模)若抛物线y 2＝2px (p >0)上的点A (2，m )到焦点的距离为6，则p ＝________.『解析』法一：由题知，2＋p2＝6，解得p ＝8.法二：由题意得⎩⎨⎧m 2＝4p ，⎝⎛⎭⎫p 2－22＋m 2＝36，解得p ＝8. 『答案』82．(2013·苏州模底)抛物线y 2＝4x 的准线方程是________．『解析』给出的是开口向右的抛物线的标准方程，其准线方程为x ＝－1. 『答案』x ＝－13．从抛物线x 2＝4y 上一点P 引抛物线准线的垂线，垂足为M ，且|PM |＝5，设抛物线的焦点为F ，则△MPF 的面积为________．『解析』由题意知，抛物线的准线方程为y ＝－1，|PM |＝|PF |＝5， ∴P 点的纵坐标为4， ∴S △MPF ＝12×5×4＝10.『答案』10『备课札记』 『类题通法』1．涉及抛物线几何性质的问题常结合图形思考，通过图形可以直观地看出抛物线的顶点、对称轴、开口方向等几何特征，体现了数形结合思想解题的直观性．2．求抛物线方程应注意的问题(1)当坐标系已建立时，应根据条件确定抛物线方程属于四种类型中的哪一种； (2)要注意把握抛物线的顶点、对称轴、开口方向与方程之间的对应关系；(3)要注意参数p的几何意义是焦点到准线的距离，利用它的几何意义来解决问题．考点二抛物线的定义应用与抛物线定义相关的最值问题常涉及距离最短、距离和最小等等.归纳起来常见的命题角度有：1动弦中点到坐标轴距离最短问题；2距离之和最小问题；3焦点弦中距离之和最小问题.角度一动弦中点到坐标轴距离最短问题1．已知抛物线x2＝4y上有一条长为6的动弦AB，则AB的中点到x轴的最短距离为________．『解析』由题意知，抛物线的准线l：y＝－1，过点A作AA1⊥l交l于点A1，过点B 作BB1⊥l交l于点B1，设弦AB的中点为M，过点M作MM1⊥l交l于点M1，则|MM1|＝|AA1|＋|BB1|2.因为|AB|≤|AF|＋|BF|(F为抛物线的焦点)，即|AF|＋|BF|≥6，所以|AA1|＋|BB1|≥6，2|MM1|≥6，|MM1|≥3，故点M到x轴的距离d≥2.『答案』2角度二距离之和最小问题2．(2014·哈尔滨四校统考)已知抛物线方程为y2＝4x，直线l的方程为x－y＋5＝0，在抛物线上有一动点P到y轴的距离为d1，到直线l的距离为d2，则d1＋d2的最小值为________．『解析』由题意知，抛物线的焦点为F(1,0)．点P到y轴的距离d1＝|PF|－1，所以d1＋d2＝d2＋|PF|－1.易知d2＋|PF|的最小值为点F到直线l的距离，故d2＋|PF|的最小值为|1＋5|＝32，所以d1＋d2的最小值为32－1.12＋－12『答案』32－1角度三焦点弦中距离之和最小问题3．已知抛物线y2＝4x，过焦点F的直线与抛物线交于A、B两点，过A、B分别作y 轴垂线，垂足分别为C、D，则|AC|＋|BD|的最小值为________．『解析』由题意知F(1,0)，|AC|＋|BD|＝|AF|＋|FB|－2＝|AB|－2，即|AC|＋|BD|取得最小值时当且仅当|AB|取得最小值．依抛物线定义知当|AB|为通径，即|AB|＝2p＝4时，为最小值，所以|AC|＋|BD|的最小值为2.『答案』2『备课札记』『类题通法』与抛物线有关的最值问题的解题策略该类问题一般情况下都与抛物线的定义有关．实现由点到点的距离与点到直线的距离的转化．(1)将抛物线上的点到准线的距离转化为该点到焦点的距离，构造出“两点之间线段最短”，使问题得解．(2)将抛物线上的点到焦点的距离转化为到准线的距离，利用“与直线上所有点的连线中垂线段最短”原理解决．考点三直线与抛物线的位置关系『典例』 (2014·无锡期末)如图，过抛物线y 2＝2px (p >0)的焦点F 的直线l 交抛物线于A ，B 两点，交其准线于点C .若BC ＝2BF ，且AF ＝3，则此抛物线的方程为________．『解析』 过点B 作BH 垂直准线于点H .由抛物线定义得BF ＝BH .因为BC ＝2BF ，所以BC ＝2BH ，则cos ∠CBH ＝BH BC ＝12，则∠CBH ＝60°，所以直线AB 的倾斜角θ＝∠CBH ＝60°，过点A 作AA ′垂直准线于点A ′，则AF ＝p ＋AF cos 60°，即3＝p ＋3×12，所以p ＝32，抛物线的方程为y 2＝3x .『答案』 y 2＝3x『备课札记』 『类题通法』求解直线与抛物线位置关系问题的方法在解决直线与抛物线位置关系的问题时，其方法类似于直线与椭圆的位置关系．在解决此类问题时，除考虑代数法外，还应借助平面几何的知识，利用数形结合的思想求解．『针对训练』(2014·南京摸底)已知抛物线y 2＝4x 的焦点为F ，准线为l .过点F 作倾斜角为60°的直线与抛物线在第一象限的交点为A ，过点A 作l 的垂线，垂足为A 1，则△AA 1F 的面积是________．『解析』法一：由题知，F (1,0)，所以l AF ：y ＝3(x －1)．将它与y 2＝4x 联立解得⎩⎨⎧x ＝3，y ＝23或⎩⎨⎧x ＝13，y ＝－233，则A (3,23)，AA 1＝AF ＝4，故S △AA 1F ＝12×4×23＝4 3.法二：设A (m,2m )，则AF ＝AA 1＝1＋m ，又m ＝1＋AF ·cos 60°＝1＋12(1＋m )，解得m＝3，所以AA 1＝4，所以S △AA 1F ＝12×4×23＝4 3.『答案』43『课堂练通考点』1．(2013·镇江期末)圆心在抛物线x 2＝2y 上，并且和抛物线的准线及y 轴都相切的圆的标准方程为________．『解析』设圆心P (2a,2a 2)，根据题设条件知抛物线的准线为y ＝－12，所以2a 2＋12＝2|a |，所以a ＝±12，所以满足条件的圆的标准方程为(x ±1)2＋⎝⎛⎭⎫y －122＝1. 『答案』(x ±1)2＋⎝⎛⎭⎫y －122＝1 2．设抛物线y 2＝6x 的焦点为F ，准线为l ，P 为抛物线上一点，P A ⊥l ，垂足为A ，如果△APF 为正三角形，那么|PF |等于________．『解析』设点P 的坐标为(x p ，y p )，则|PF |＝x p ＋32.过点P 作x 轴的垂线交x 轴于点M ，则∠PFM ＝∠APF ＝60°，所以|PF |＝2|MF |，即x p ＋32＝2⎝⎛⎭⎫x p －32，解得x p ＝92，所以|PF |＝6. 『答案』63．过抛物线y 2＝8x 的焦点F 作倾斜角为135°的直线交抛物线于A ，B 两点，则弦AB 的长为________．『解析』抛物线y 2＝8x 的焦点F 的坐标为(2,0)，直线AB 的倾斜角为135°，故直线AB 的方程为y ＝－x ＋2，代入抛物线方程y 2＝8x ，得x 2－12x ＋4＝0.设A (x 1，y 1)，B (x 2，y 2)，则弦AB 的长|AB |＝x 1＋x 2＋4＝12＋4＝16.『答案』164．设抛物线x 2＝12y 的焦点为F ，经过点P (2,1)的直线l 与抛物线相交于A ，B 两点，又知点P 恰为AB 的中点，则|AF |＋|BF |＝________.『解析』分别过点A ，B ，P 作准线的垂线，垂足分别为M ，N ，Q ，根据抛物线上的点到焦点的距离等于该点到准线的距离，得|AF |＋|BF |＝|AM |＋|BN |＝2|PQ |＝8.『答案』85．(2013·扬州三调)抛物线y 2＝4mx (m >0)的焦点到双曲线x 216－y 29＝1的一条渐近线的距离为3，则此抛物线的方程为________．『解析』因为双曲线渐近线为x 4±y 3＝0，抛物线的焦点为(m,0)，所以由|3m |5＝3得m ＝5，所以抛物线的方程为y 2＝20x .『答案』y 2＝20x。