第二章 拉伸、压缩与剪切

第
二
章
拉伸压缩与剪切
1
பைடு நூலகம்
§2-1

轴向拉伸与压缩的概念和实例
轴向拉伸——轴力作用下，杆件伸长 （简称拉伸） 轴向压缩——轴力作用下，杆件缩短 （简称压缩）

2
拉、压的特点：

1.两端受力——沿轴线，大小相等，方向相反 2. 变形—— 沿轴线
3

§2-2 轴向拉伸或压缩时横截面上的内力和应力
1 、横截面上的内力
A3
2
l1 l2 y AA3 A3 A4 sin 30 tan 30 2 1.039 3.039mm
A
A A4
AA x2 y2 0.6 2 3.039 2 3.1mm
40
目录
例 2—5 截面积为 76.36mm² 的钢索绕过无摩擦的定滑轮 F=20kN，求刚索的应力和 C点的垂直位移。 （刚索的 E =177GPa，设横梁ABCD为刚梁）
16
§2-4

材料在拉伸时的力学性能
材料的力学性能是指材料在外力的作用下表现出的变 形和破坏等方面的特性。

现在要研究材料的整个力学性能（应力 —— 应变）：
从受力很小
破坏
理论上——用简单描述复杂
工程上——为（材料组成的）构件当好医生
17
一、 低碳钢拉伸时的力学性能 （含碳量<0.3%的碳素钢）
力均匀分布于横截面上，σ等于常量。于是有：
N d A d A A
A A
得应力：

N A
F
FN
σ
10
例题2-2
A 1
45°
C
2

第2章拉伸压缩与剪切教学目的：了解材料的力学性质；掌握轴向拉伸、压缩、剪切和挤压的概念；掌握轴向拉压时构件的内力、应力、变形的计算；熟练掌握剪切应力及挤压应力的计算方法并进行强度校核；掌握拉压杆的超静定问题。

教学重点：建立弹性杆件横截面上内力、内力分量的概念；运用截面法画轴力图；掌握低碳钢的力学性质；掌握轴向拉伸和压缩时横截面上正应力计算公式及其适用条件；掌握拉压杆的强度计算；熟练掌握剪切和挤压的实用计算。

教学难点：低碳钢类塑性材料在拉伸过程中反映出的性质；许用应力的确定和使用安全系数的原因；强度计算问题；剪切面和挤压面的确定；剪切和挤压的实用计算；拉压杆超的静定计算。

教具：多媒体。

教学方法：采用启发式教学，通过提问，引导学生思考，让学生回答问题。

举例掌握轴向拉伸、压缩和剪切变形概念，通过例题、作业，加强辅导熟练运用截面法，掌握轴力图的画法；建立变形、弹性变形、应变、胡克定律和抗拉压刚度的概念；教学内容：轴向拉伸和压缩的概念；强度计算；材料的力学性能及应力应变图；许用应力与安全系数；超静定的计算；剪切概念；剪切实用计算；挤压实用计算。

教学学时：8学时。

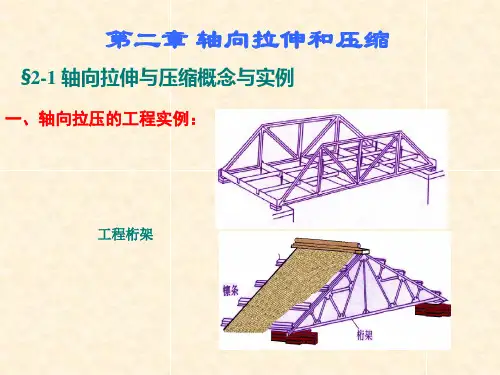
教学提纲：2.1 轴向拉伸与压缩的概念和实例1．实例（1）液压传动中的活塞杆（2）内燃机的连杆（3）起吊重物用的钢索（4）千斤顶的螺杆（5）桁架的杆件2．概念及简图这些杆件虽然外形各异，受力方式不同，但是它们有共同的特点：（1）受力特点：作用在杆件上的外力合力的作用线与杆件轴线重合，杆件变形是沿轴线方向的伸长或缩短。

（如果两个F 力是一对离开端截面的力，则将使杆发生纵向伸长，这样的力称为轴向拉力； 如果是一对指向端截面的力，则将使杆发生纵向缩短，称为轴向压力）。

（2）变形特点：主要变形是纵向伸长或缩短。

（3）拉（压）杆的受力简图：（4）说明：本章所讲的变形是指受压杆没有被压弯的情况下，不涉及稳定性问题。

2.2 轴向拉伸或压缩时横截面上的内力和应力1．截面法求内力(1)假想沿m-m 横截面将杆切开(2)留下左半段或右半段(3)将弃去部分对留下部分的作用用内力代替(4)对留下部分写平衡方程，求出内力（即轴力）的值。

拉伸和压缩是杆件基本受力与变形形式 中最简单的一种，所涉及的一些基本原理与方 法比较简单，但在材料力学中却有一定的普遍 意义。
承受轴向载荷的拉（压）杆在工程中的应用 非常广泛。
一些机器和结构中所用的各 种紧固螺栓，在紧固时，要对螺 栓施加预紧力，螺栓承受轴向拉 力，将发生伸长变形。
承受轴向载荷的拉（压）杆在工程中的应用 非常广泛。
FN F A A
0 , max p sin cos sin sin 2 45 , max 2
2
A A F F F cos F F F p cos cos A A A p 2 k
一 试 件 和 实 验 条 件
常 温 、 静 载
材料压缩时的力学性能
二 塑 性 材 料 （ 低 碳 钢 ） 的 压 缩
p —
S —
比例极限
e —
弹性极限
屈服极限 E --- 弹性摸量
拉伸与压缩在屈服 阶段以前完全相同。
材料压缩时的力学性能
三 脆 性 材 料 （ 铸 铁 ） 的 压 缩 脆性材料的抗拉与抗压性质不完全 相同 压缩时的强度极限远大于拉伸时的 强度极限 bc bt
观察变形：
横向线ab、cd仍为直线，且仍垂直于杆轴 线，只是分别平行移至a’b’、c’d’。
F
a b
a
b
c
d
c d
F
平面假设—变形前原为平面的横截面， 变形后仍保持为平面且仍垂直于轴线。
直杆轴向拉伸或压缩时横截面上的内力和应力
从平面假设可以判断： （1）所有纵向纤维伸长相等
（2）因材料均匀，故各纤维受力相等 （3）内力均匀分布，各点正应力相等，为常量

22
屈服极限的确定方法
σ
b
0.2
o
0.2%
在ε轴上取0.2％的点, 对此点作平行于σ－ε曲线 的直线段的直线（斜率亦为 E）,与σ－ε曲线相交点对 应的应力即为σ0.2 .
ε
σb是衡量脆性材料强度的唯一指标。
材料力学 土木工程系 陈爱萍
23
§2.5 材料压缩时的力学性能
国家标准规定《金属压缩试验方法》（GB7314—87)
材料力学 土木工程系 陈爱萍
28
§2.7 失效、 安全因数和强度计算
一、极限应力、安全系数、许用应力
材料破坏时的应力称为极限应力。 由于各种原理使结构丧失其正常工作能力的现象，称为失效

jx


s b
塑性材料 脆性材料
构件工作时允许达到的最大应力值称许用应力
jx
n
材料力学 土木工程系 陈爱萍
(3) 必须是等截面直杆，否则横截面上应力将不是均匀 分布，当截面变化较缓慢时，可近似用该公式计算。
材料力学 土木工程系 陈爱萍
12
§2.3 直杆拉伸或压缩时斜截面上的应力
F
FF


p cos
FN A
cos cos2


p
sin
cos sin
1 sin 2
材料力学 土木工程系 陈爱萍
37
求解超静定问题的基本步骤：
（1）平衡方程； （2）几何方程——变形协调方程； （3）物理方程——弹性定律； （4）补充方程：由几何方程和物理方程得； （5）解由平衡方程和补充方程组成的方程组。
材料力学 土木工程系 陈爱萍
38

实验装置与测量装置
试验装置对材料的测试很重要，因为它确保了精度和准确性。测量装置应该能够准确测量试 样的形变和载荷。
数据分析方法
在进行测试之后，数据和结果的分析非常重要。需要注意的是本构关系和试验结果分析是经 验丰富的材料学家可以提出的有价值的见解。
结论与展望
结论
本课程介绍了有关材料力学中拉伸、压缩和 剪切实验的基本原理和关键技术。我们可以 将学到的知识应用到工程实践和材料创新上。
2ቤተ መጻሕፍቲ ባይዱ本构关系
本构关系是指应力和应变之间的关系。材料力学中存在两种流变学问题，弹性问题和塑 性问题。两者的本构关系分别为线性弹性本构关系和极限强度本构关系。
3 欧拉梁方程
欧拉梁方程使用到了杆的几何性质，指出一个杆稳定的条件。当所受外力P不大于欧拉推 力F时，杆件就是稳定的。
压缩测试
杆件的短缩假设
短缩假设是细长杆压缩稳定 性问题的基础。它假设杆件 压缩后仍保持直线，不会产 生剪切变形和弯曲；所有点 的变形相同，仍使用单一变 量表示。
材料力学第二章-拉伸、 压缩与剪切课件
欢迎来学习关于材料拉伸、压缩和剪切的课程！在这个课程中，你将学习杆 件的细长假设、短缩假设、本构关系和欧拉梁方程。我们还会介绍应力与应 变关系、应力平面和变形观察以及破坏理论。
拉伸测试
1 杆件的细长假设
细长假设的出现是为了简化问题。它假设杆件在拉伸过程中保持直线，不产生弯曲；所 有点的变形相同，因此可以用单一变量来表示。
2
应力平面与变形观察
理解应力与应变之间的关系是剪切测试的关键。我们需要通过变形的观察来确定 应力平面。
3
破坏理论
剪切测试最终会导致杆件的破坏。多数材料的 yield strength 是其快速破坏前所能 承受的最大应力，这个应力被称作杆件的最大应力。

Fp
（1）接触面为平面
Fp
Ap—实际接触面面积
挤压力 Fp= F
（2）接触面为圆柱面
Ap—直径投影面面积
2.8 剪切和挤压的实用计算
d
δ Ap d
(a)
(b)
(cd)
挤压强度条件：
p
Fp Ap
p
p 许用挤压应力，常由实验方法确定
塑性材料： p 1.5 2.5 脆性材料： p 0.9 1.5
2.4 轴向拉伸或压缩时的变形
对于变截面杆件（如阶梯
杆），或轴力变化。则：
l
li
FNili Ei Ai
2.5 材料在拉伸和压缩时的力学性能
力学性能：在外力作用下材料在变形和破坏方 面所表现出的力学特性。 2.5.1 材料在拉伸时的力学性能
一
试
件
和
常
实 验 条 件
温 、 静 载
2.5 材料在拉伸和压缩时的力学性能
一、纵向变形
l l1 l
l
l
F
{ FN F AA E E l l
l FNl Fl EA EA
l F,l l 1
EA
l
l1
二、横向变形
F b1 b
b b1 b
b
b
泊松比
横向应变
EA为抗拉刚度
钢材的E约为200GPa，μ约为0.25—0.33
2.4 轴向拉伸或压缩时的变形
即螺栓的轴力为
FN
F 6
π D2 p 24
根据强度条件
max
FN A
得
A
FN
即
d 2
4
D2 p
24
螺栓的直径为 d

拉伸—拉力，其轴力为正值。方向背离所在截面。 压缩—压力，其轴力为负值。方向指向所在截面。
F
N （＋） N
F
F
N （－） N
F
轴力一般按正方向假设。
3、轴力图： 轴力沿轴线变化的图形
F
F
N
4、轴力图的意义
+ x
① 直观反映轴力与截面位置变化关系；
② 确定出最大轴力的数值及其所在位置，即确定危险截面位置，为 强度计算提供依据。
1、低碳钢轴向拉伸时的力学性质 (四个阶段)
⑴、弹性阶段:OA
OA’为直线段； E
AA’为微弯曲线段。
p —比例极限； e —弹性极限。
一般这两个极限相差不大， 在工程上难以区分，统称为弹 性极限
低碳钢拉伸时的四个阶段
⑴、弹性阶段:OA, ⑵、屈服阶段:B’C。
s —屈服极限
屈服段内最低的应力值。
例 图示杆的A、B、C、D点分别作用着大小为FA = 5 F、 FB = 8 F、 FC = 4 F FD= F 的力，方向如图，试求各段内力并画出杆的轴力图。
OA
BC
D
FA
FB
FC
FD
N1
A
BC
D
FA
FB
FC
FD
解： 求OA段内力N1：设截面如图
X 0 FD FC FB FA N1 0
N4= F
FD
N1 2F , N2= –3F， N3= 5F， N4= F
N1 2F , N2= –3F， N3= 5F， N4= F
轴力图如下图示
OA
BC
D
FA
FB
FC
FD
N 2F
5F

o 0.2%
2）.脆性材料的力学性质
对于脆性材料（铸铁），拉伸时的应力应 变曲线为微弯的曲线，没有屈服和缩颈现象， 试件突然拉断。断后伸长率约为0.45%。为 典型的脆性材料。
bt
o
σbt—拉伸强度极限（约为140MPa）。它是
衡量脆性材料（铸铁）拉伸的唯一强度指标。
三、材料在压缩时的力学性能
3
3F
2
1
2F
F=10kN
3
2
1
解：3.计算3-3截面的内力
3 3F FN3
2F
F=10kN
3
Fx 0
F 2F 3F FN3 0 FN3 2F 20kN
例2.2 计算图示杆件指定截面上的轴力，并画出杆件的轴力图。
3
3F
2
1
2F
F=10kN
3
2
1
解：4.轴力图
FN/kN
FN1 F 10kN FN 2 F 10kN FN3 2F 20kN
§2.3 材料拉伸和压缩时的力学性能
常温、静载试验
一、试件（试样）
d 10mm, lo 100mm
二、材料在拉伸时的力学性能
1.低碳钢材料
低碳钢的拉伸应力-应变曲线
d
b
e P
c
a
s
d g
o
明显的四个阶段
1、弹性阶段ob
e
b
f
f h
E
2、屈服阶段bc（失去抵 抗变形的能力）
s — 屈服极限
3、强化阶段ce（恢复抵抗 变形的能力）
b — 强度极限
4、局部变形阶段ef
P — 比例极限 e — 弹性极限
E tan

FN
2P +
3P
x
PAG 21
Northeastern University
§2-2
轴向拉伸和压缩时的内力
例2-2 图示等直杆长为L,受分布载荷q = kx的作用(以A端为原 点),试画出杆的轴力图。 解:以距A端为x的一段为研究对象 q(x)
A L q(x) qL FN x 0 B q(x) x
轴力：轴向拉压时的内力 垂直于横截面、过截面形心
正负规定：
（1）若轴力的指向背离截面，则规定为正的，称为拉力
（2）若轴力的指向指向截面，则规定为负的，称为压力 FN F FN F 轴力为正 轴力为负 以拉为正，以压为负
PAG 15
Northeastern University
§2-2
F F
A C
B
C
F
A
FN
1、截开 在要求内力处,用一假想截面沿杆横截面截开, 以其中受力较为简单的一部分作为研究对象,弃去另 一部分；
PAG 12
Northeastern University
§2-2
轴向拉伸和压缩时的内力
三、求内力的截面法
设图示等直杆在两端轴向拉力 F 的作用下处于平衡， 求杆 AB上截面C处的内力
PAG 28
Northeastern University
§2-3
轴向拉伸和压缩时的应力
3、拉伸应力
F F F

FN
FN 由静力学可得合力 FN dFN d A A A A
PAG 29
Northeastern University
§2-3
轴向拉伸和压缩时的应力
FNa2 F (拉力)

⊕
Ⅰ － ○ 20 kN
⊕
F
x
0
FN1
Ⅰ 80kN Ⅱ
FN2 60 80 0
FN2 20kN
FN2 第三段:
Ⅲ
30kN
60kN
F
x
0
Ⅱ
FN3 30 0
FN3 30kN
FN3
Ⅲ
例2
3kN
画图示杆的轴力图
2kN 2kN 10 kN 4kN 8kN
A
3kN
B
C
D
脆性材料 u （ bc） bt

u
n

n —安全因数 —许用应力

塑性材料的许用应力
脆性材料的许用应力
s
ns
bt
nb
p 0.2 n s bc n b
§2-6
§2-7 失效、安全因数和强度计算
解： A 轴力图
A1 B
○ －
A2 60kN 20 kN C D 20 kN ⊕
AB
BC
CD
FN AB 40 103 20MPa A1 2000 FN BC 40 103 40MPa A2 1000 FN CD 20 103 20MPa A2 1000
3、轴力正负号：拉为正、 F 压为负
0 FN F 0 FN F
F
§2-2
x
4、轴力图：轴力沿杆件轴 线的变化
目录
例1
60kN
画图示杆的轴力图
Ⅰ
80kN
Ⅱ
Ⅲ 50kN
30kN
第一段:

x1 0,
FN2 F ;
x1 2l , FN2 F
23
FN1=F
由以上结果画出轴力图 F
A
B
FN3=F
F q l
F
C D
l
F
2l
l
F
+ +
F
F
FN 图
24
1. 求分布荷载作用的BC段的轴力时，作截面之前 不允许用合力2lq＝2F代替分布荷载。
q F l
F
A l
B
F 2l
C
37
二、 斜截面上的应力
变形假设：两平行的斜截面在杆受拉(压)而变形后仍相互平行。 两平行的斜截面之间的所有纵向线段伸长变形相同。 以 p表示斜截面 k-k上的 应力，于是有
k
因： 得：
A A cos
F p A
F

k
F
k
F F
F
F F p cos s cos A A
43
温度、速率的影响
44
2.试验设备
微机控制电子万能试验机
引伸计
45
二、拉伸试验
1. 低碳钢拉伸时的力学性质
低碳钢是指含碳量在0.3%以下的碳素钢。 （1）拉伸试样 先在试样中间等直部分上 划两条横线，这一试验段长度 称为标距 l d
l
标距
圆截面试样：l = 10d 或 l = 5d 矩形截面试样： 11.3 A 或 l 5.65 A。 l
7
F
§2–2
一、内力
内力计算
m F m 设一等直杆在两端轴向拉力 F 的作用下处于平衡,求杆件横 截面 m-m 上的内力.
8

1.了解轴向拉伸、压缩的受力和变形特点 2.掌握轴力的计算和轴力图的画法 3.掌握拉压杆横截面上正应力的计算方法 4.了解低碳钢和铸铁材料的机械性能
5.能熟练运行强度条件进行计算 6.掌握纵向、横向的变形计算 7.初步掌握拉、压超静定问题的解法 8.理解温度应力和装配应力产生的原因；
9.了解应力集中的概念、发生部位及其危害
强度极限最高； (2)刚度看各种材料的图线中，哪个
材料的斜率最大； (3)塑性看拉断后哪个材料的延伸率大。
-
26
跟踪训练
三种材料的应力-应变曲线分别为如图a,b,c所示， 其中材料强度最高的是： a 弹性模量最大的是： b 塑性最好的是： c
-
27
五、铸铁拉伸时的力学性能
对于脆性材料（铸铁），拉伸时的应力应 变曲线为微弯的曲线，没有屈服和径缩现象， 试件突然断裂。断后伸长率约为0.5%。为典 型的脆性材料。
移
-
49
2）变形分析，求各段的变形
lD BN E Dl1 D BA B 2 1 4 11 0 13 2 0 0 1.5 4 0 0.0 5 13 0 m 缩 ( 短 lC DN E Cl2 C D A D 2 1 4 11 0 13 4 0 0 1 .5 4 0 0.02 15 3 0 m 缩 ( 短 lAC N E AlC 2 AA C 2 6 1 1 1 0 1 34 0 0 1 .54 00.03 1 7 3 0 5 m 伸 ( 长
等直杆受力如图所示，其轴力图应是( )
-
12
二、拉伸或压缩横截面上的应力
杆件的强度不仅与轴力有关，还与横截面面 积有关。必须用应力来比较和判断杆件的强度。
P
N
dA
N AdA
-

第二章拉伸、压缩与剪切小结一、轴向拉压杆的内力轴力轴向拉压时，杆件横截面上内力的合力，用FN 表示。

轴力正负号的规定杆件受拉而伸长的轴力为正，受压而缩短的轴力为负。

或者表述为FN 的方向与截面外法线方向一致的为正，反之为负。

轴力的求法截面法，一般将所求截面的内力假设为正的数值，这一方法称为“设正法”。

如结果为正，则说明假设正确，是拉力；如是负值，则说明假设错误，是压力。

轴力图注意：1.轴力图与杆件应注意一一对应关系，习惯上在其值变化的角点标出数值；2.作图或校核时注意应用突变关系，即在外力作用面，轴力图突变，突变值（绝对值）的大小等于作用在该面的外力的大小；3.同一图应采用同一比例；二、应力1）横截面上的应力平面假设：变形前为平面的横截面，变形后仍保持为平面且仍垂直于轴线。

由材料的假设可知，轴向拉压杆横截面上各点的应力相等，垂直于截面，用表示，即：使用条件:①外力的合力作用线必须与杆件轴线重合②当杆件的横截面沿轴线方向变化缓慢，而且外力作用线与杆件轴线重合时，也可近似地应用该公式。

③不适用于集中力作用点附近的区域圣维南原理:作用于弹性体上某一局部区域内的外力系，可以用与它静力等效的力系来代替。

σNF Aσ=2)斜截面上的应力轴向拉压时斜截面上的应力随其方位而变化总应力：正应力：切应力：三、材料的力学性能1）低碳钢拉伸4个阶段：弹性阶段、屈服（流动）阶段、强化阶段、局部变形（颈缩）阶段。

4个极限应力：比例极限，弹性极限，屈服极限，强度极限两个塑性指标：延伸率和断面收缩率一个弹性模量ασααcos cos ==AF p ασασαα2cos cos ==p ασαταα2sin 2sin ==p %1001⨯-=ll l δ%1001⨯-=A A A ψE σε=2）其它材料的拉伸3）材料压缩时的力学性能塑性材料压缩时的力学性质与拉伸时的基本无异。

脆性材料拉、压力学性能有较大差别，抗压能力明显高于抗拉能力。

4F 4 20103 N 145.5 MPa (D2 d 2 ) (0.022 0.0152 ) m2
因为 156 MPa 所以满足强度校核。
湖南大学力 学系:肖万伸
例：结构中 BC 和 AC 都是圆截面直杆，直径均为d=20mm. BC为 Q235钢杆，其许用应力[]1=160MPa; AC为木杆，其许用应力 []2=7MPa。求：该结构的许可载荷。
l1：杆件变形后长度； l：伸长量；
b：杆件原宽；
b ：形后杆件宽度。 1
湖南大学力 学系:肖万伸
拉压杆件在轴向变形的同时，横向也会发生变化。
试验结果表明，当拉压杆件的应力不超过材料比例极 限时，与的比值的绝对值为一常数，即
结论：每条纵向纤维的力学性能相同，其受力也应 相同，因此横截面上的正应力是均匀分布的 .
3.等截面拉(压)杆横截面上正应力的计算公式
式中， FN 为轴力，A 为杆的横截面面积,
湖南大学力 学系:肖万伸
的符号与轴力FN 的符号相同。
当轴力为正号时（拉伸），正应力也为正号，称为拉应 力 ;当轴力为负号时（压缩），正应力也为负号，称为压 应力 。 该公式的适应范围：
F qA
q
杆端作用集中力，横截面应力均匀分布吗？ 圣维南原理：如将作用于构
q
件上某一小区域内的外力系
q
（外力大小不超过一定值）
q
用一静力等效力系来代替，
则这种代替对构件内应力与
F
max 应变的影响只限于离原受力
小区域很近的范围内。对于
F
杆件，此范围相当于横向尺
F
F 寸的1～1.5倍。
湖南大学力 学系:肖万伸
湖南大学力 学系:肖万伸
切应变
构件产生变形时，不仅线段的长度会发生改变，正

2
2
FN1 1
F, 3
FN2 1
F 3
FN1 1 23 F,
FN2

2 1
3
F
第二章 拉伸、压缩与剪切
按AC
FN1

A1


1

200160

32kN

F

1

1

2
3

FN1


1

2
3

32

61.8kN
按BC
FN2

A2

2

300100

30kN
# 应力－应变图
e
F
e
d
d c
f
c
f
b a
ab
O F-Dl曲线
Dl O
– 曲线
Dl l
第二章 拉伸、压缩与剪切
变形的四个阶段
① 弹性阶段 oa ab
滑移线

② 屈服阶段
c
屈服现象：应力不增加， b
应变不断增加的现象
a
e f
③ 强化阶段 ce
④ 局部变形阶段 ef
O
弹性 屈服 强化
F l l1
b1 b
# 横向应变 Db
b
# 试验结果表明，当 < p 时，


称为泊松比，是一个材料常数，无量纲
或写成 （负号表示横向与轴向变形的方向相反）
第二章 拉伸、压缩与剪切
E 最重要的两个材料弹性常数
几种常用材料的 E 和 的值
材料名称

全应力（总应力）： 是矢量
F
M A
p = lim
ΔA0
ΔF dF = ΔA dA
临沂大学 汽车学院
材料力学
全应力分解为：
第二章 拉伸、压缩与剪切
垂直于截面的应力称为“正应力”:
ΔFN dFN = lim = dA ΔA0 ΔA
p

M

位于截面内的应力称为“剪应力、切应力”:
ΔFS dFS = lim = dA ΔA0 ΔA
x
x
C
FN 1 sin 45 - F = 0

2
FN 1 = 28.3kN FN 2 = -20kN
临沂大学 汽车学院
材料力学
A 1
45°
第二章 拉伸、压缩与剪切
2、计算各杆件的应力。
B
C
2
FN 1 28.3 103 1 = = = 90MPa A1 20 2 4
FN 1
y
F
FN 2 45° B
F
I
FN
FN’
II
F
x
SF =0：-F +F=0； F =F SFXX=0：FN-F=0； FN=F N’ N’
临沂大学 汽车学院
•3、轴力：截面上的 内力 •由于外力的作用线 与杆件的轴线重合， 内力的作用线也与杆 件的轴线重合。所以 称为轴力。
材料力学
第二章 拉伸、压缩与剪切
•答案：C
临沂大学 汽车学院
2-2截面： 1）取（d）图
F1 - F2 - FN 2 = 0 FN 2 = 1.32kN (压)
2）取（e）图
FN 2 - F3 = 0
临沂大学 汽车学院

义与分类
总结词
了解拉伸的定义和分类是理解材料力 学的基础。
详细描述
拉伸是指材料受到轴向拉伸或压缩的 外力作用，使材料产生伸长或缩短的 变形。根据外力性质，拉伸可分为弹 性拉伸、塑性拉伸和粘性拉伸等。
拉伸的应力和应变
总结词
应力和应变是描述材料在拉伸过程中受力与变形的关键参数。
在压缩过程中，当材料的 应力超过其抗压强度时， 材料会发生弯曲或断裂。
剪切失效
在剪切过程中，当材料的 剪切应力超过其抗剪强度 时，材料会发生相对滑移 。
材料在拉伸、压缩与剪切中的强度指标
抗拉强度
抗剪强度
材料在拉伸过程中所能承受的最大应 力。
材料在剪切过程中所能承受的最大剪 切应力。
抗压强度
材料在压缩过程中所能承受的最大应 力。
压缩的强度条件
强度条件
在压缩过程中，物体抵抗破坏的能力称为强度条件。
强度条件公式
根据材料力学理论，强度条件公式为σ≤[σ]，其中σ为材料的许用应力，[σ]为材 料的极限应力。
2023
PART 04
剪切力学
REPORTING
剪切定义与分类
剪切定义
剪切是材料在剪切力作用下沿剪切面发生相对滑动的现象。
详细描述
应力是指在单位面积上所受的外力，是衡量材料受力状态的物理量。应变则表示材料长度或体积的变化程度，用 于描述材料的变形程度。在拉伸过程中，应力和应变之间存在一定的关系，这种关系称为应力-应变曲线。
拉伸的强度条件
总结词
强度条件是评估材料在拉伸过程中所能承受的最大应力的关 键指标。
详细描述
强度条件通常通过实验测定，并根据材料的性质和用途进行 分类。常见的强度条件包括抗拉强度、屈服强度和疲劳强度 等。这些强度条件对于材料的选择和使用具有重要的指导意 义。