下载文档原格式
3第二章有限差分方法基础解读有限差分方法是数值计算中常用的一种方法，用于求解偏微分方程的数值解。
它的基本思想是将连续的空间或时间域离散化为有限的点，然后用差分近似代替导数，将偏微分方程转化为差分方程，从而得到问题的数值解。
有限差分方法的基础概念有三个：差分节点、差分近似和差分方程。
差分节点是指将连续的自变量区域划分为离散的点，这些点被称为节点。
差分近似是指用函数在差分节点上的函数值来近似代替它们的导数值。
差分方程是指在差分节点上建立的方程，用来表示问题的数值解。
在有限差分方法中，常用的几种差分格式有：向前差分、向后差分和中心差分。
其中，向前差分是将函数在节点$x_i$处的导数近似为$f'(x_i)≈\frac{f(x_i+h)-f(x_i)}{h}$，向后差分是将函数在节点$x_i$处的导数近似为$f'(x_i)≈\frac{f(x_i)-f(x_i-h)}{h}$，中心差分是将函数在节点$x_i$处的导数近似为$f'(x_i)≈\frac{f(x_i+h)-f(x_i-h)}{2h}$。
这些差分格式的选择要根据问题的具体情况和求解的精度要求来确定。
有限差分方法中，差分方程的建立是非常重要的一步。
一般来说，差分方程的建立需要利用边界条件和初始条件。
对于初始条件，通常是指给定问题在初始时刻或初始位置上的条件；而边界条件是指给定问题在边界上的条件。
缺乏良好的边界条件和初始条件会导致差分方程无法建立或无法得到合理的数值解。
因此，在使用有限差分方法求解偏微分方程时，需要仔细考虑问题的边界条件和初始条件，并将其合理地纳入差分方程中。
有限差分方法还包括时间步长和空间步长的选择。
时间步长是指时间域上的离散间隔，空间步长是指空间域上的离散间隔。
时间步长和空间步长的选取要兼顾问题的稳定性和精度要求。
一般来说，时间步长和空间步长越小，计算的精度越高，但计算量也会增加。
因此，在具体应用中，需要根据问题的特点和计算资源的限制来选择合适的步长。
亥姆霍兹方程有限差分法
亥姆霍兹方程是一个描述电磁波的椭圆偏微分方程，以德国物理学家亥姆霍兹的名字命名。
有限差分法是求解亥姆霍兹方程的一种常用数值方法。
有限差分法的基本思想是将求解区域离散为网格，然后使用中心差分格式来逼近微分算子。
这种方法的优势在于其简单性和易于实现，通过适当选择网格分辨率，可以获得足够的精度。
同时，研究者们也在不断探索如何构造高精度、收敛快且针对大波数问题有效的有限差分格式。
然而，有限差分法在求解高波数问题时可能会遇到一些困难，因为Helmholtz方程的解在高波数时会出现严重的震荡，导致数值解的精度随着波数的增加而逐渐变差，即所谓的“污染效应”。
为了解决这个问题，研究者们提出了各种优化差分系数的方法来提高数值精度。
总的来说，有限差分法是一种有效且实用的求解亥姆霍兹方程的方法，但在实际应用中需要根据具体问题的特点和要求进行选择和调整。
1. 引言有限差分法（Finite Difference Method，FDM）是一种求解微分方程数值解的近似方法，其主要原理是对微分方程中的微分项进行直接差分近似，从而将微分方程转化为代数方程组求解。
有限差分法的原理简单，粗暴有效，最早由远古数学大神欧拉（L. Euler 1707-1783）提出，他在1768年给出了一维问题的差分格式。
1908年，龙格（C. Runge 1856-1927）将差分法扩展到了二维问题【对，就是龙格-库塔法中的那个龙格】。
但是在那个年代，将微分方程的求解转化为大量代数方程组的求解无疑是将一个难题转化为另一个难题，因此并未得到大量的应用。
随着计算机技术的发展，快速准确地求解庞大的代数方程组成为可能，因此逐渐得到大量的应用。
发展至今，有限差分法已成为一个重要的数值求解方法，在工程领域有着广泛的应用背景。
本文将从有限差分法的原理、基本差分公式、误差估计等方面进行概述，给出其基本的应用方法，对于一些深入的问题不做讨论。
2. 有限差分方法概述首先，有限差分法是一种求解微分方程的数值方法，其面对的对象是微分方程，包括常微分方程和偏微分方程。
此外，有限差分法需要对微分进行近似，这里的近似采取的是离散近似，使用某一点周围点的函数值近似表示该点的微分。
下面将对该方法进行概述。
2.1. 有限差分法的基本原理这里我们使用一个简单的例子来简述有限差分法的基本原理，考虑如下常微分方程\begin{cases} u'(x)+c(x)u(x)=f(x), \quad x \in [a, b]; \\u(x=a) = d \end{cases} \tag{1}微分方程与代数方程最大的不同就是其包含微分项，这也是求解微分方程最难处理的地方。
有限差分法的基本原理即使用近似方法处理微分方程中的微分项。
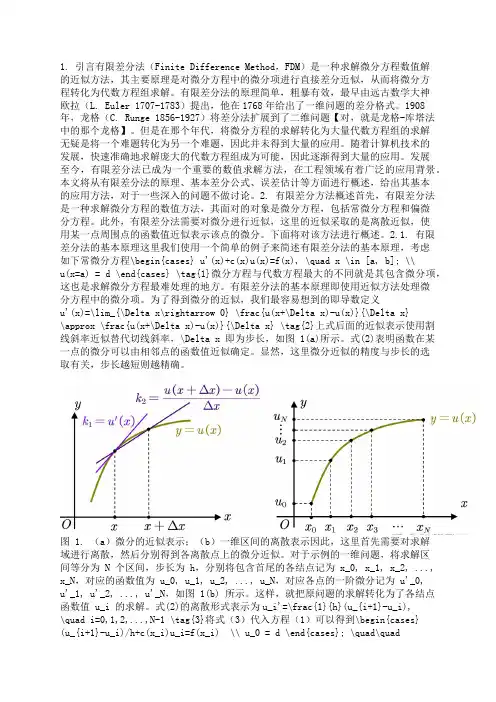
为了得到微分的近似，我们最容易想到的即导数定义u'(x)=\lim_{\Delta x\rightarrow 0} \frac{u(x+\Delta x)-u(x)}{\Delta x}\approx \frac{u(x+\Delta x)-u(x)}{\Delta x} \tag{2}上式后面的近似表示使用割线斜率近似替代切线斜率，\Delta x 即为步长，如图 1(a)所示。
有限差分法（ Finite Difference Method，简称FDM）是数值方法中最经典的方法，也是计算机数值模拟最早采用的方法，至今仍被广泛运用。
该方法将求解域划分为差分网格，用有限个网格节点代替连续的求解域。
有限差分法以Taylor级数展开等方法，把控制方程中的导数用网格节点上的函数值的差商代替进行离散，从而建立以网格节点上的值为未知数的代数方程组。
该方法是一种直接将微分问题变为代数问题的近似数值解法，数学概念直观，表达简单，是发展较早且比较成熟的数值方法。
对于有限差分格式，从格式的精度来划分，有一阶格式、二阶格式和高阶格式。
从差分的空间形式来考虑，可分为中心格式和逆风格式。
考虑时间因子的影响，差分格式还可以分为显格式、隐格式、显隐交替格式等。
目前常见的差分格式，主要是上述几种形式的组合，不同的组合构成不同的差分格式。
差分方法主要适用于有结构网格，网格的步长一般根据实际地形的情况和柯朗稳定条件来决定。
构造差分的方法有多种形式，目前主要采用的是泰勒级数展开方法。
其基本的差分表达式主要有三种形式：一阶向前差分、一阶向后差分、一阶中心差分和二阶中心差分等，其中前两种格式为一阶计算精度，后两种格式为二阶计算精度。
通过对时间和空间这几种不同差分格式的组合，可以组合成不同的差分计算格式。
下面我们从有限差分方法的基本思想、技术要点、应用步骤三个方面来深入了解一下有限差分方法。
1.基本思想有限差分算法的基本思想是把连续的定解区域用有限个离散点构成的网格来代替，这些离散点称作网格的节点；把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似；把原方程和定解条件中的微商用差商来近似，积分用积分和来近似，于是原微分方程和定解条件就近似地代之以代数方程组，即有限差分方程组，解此方程组就可以得到原问题在离散点上的近似解。
然后再利用插值方法便可以从离散解得到定解问题在整个区域上的近似解。
在采用数值计算方法求解偏微分方程时，再将每一处导数由有限差分近似公式替代，从而把求解偏微分方程的问题转换成求解代数方程的问题，即所谓的有限差分法。
2.技术要点如何根据问题的特点将定解区域作网格剖分；如何把原微分方程离散化为差分方程组以及如何解此代数方程组。
此外为了保证计算过程的可行性和计算结果的正确性，还需从理论上分析差分方程组的性态，包括解的唯一性、存在性和差分格式的相容性、收敛性和稳定性。
对于一个微分方程建立的各种差分格式，为了有实用意义，一个基本要求是它们能够任意逼近微分方程，这就是相容性要求。
另外，一个差分格式是否有用，最终要看差分方程的精确解能否任意逼近微分方程的解，这就是收敛性的概念。
此外，还有一个重要的概念必须考虑，即差分格式的稳定性。
因为差分格式的计算过程是逐层推进的，在计算第n+1 层的近似值时要用到第 n 层的近似值，直到与初始值有关。
前面各层若有舍入误差，必然影响到后面各层的值，如果误差的影响越来越大，以致差分格式的精确解的面貌完全被掩盖，这种格式是不稳定的，相反如果误差的传播是可以控制的，就认为格式是稳定的。
只有在这种情形，差分格式在实际计算中的近似解才可能任意逼近差分方程的精确解。
关于差分格式的构造一般有以下 3 种方法。
最常用的方法是数值微分法，比如用差商代替微商等。
另一方法叫积分插值法，因为在实际问题中得出的微分方程常常反映物理上的某种守恒原理，一般可以通过积分形式来表示。
此外还可以用待定系数法构造一些精度较高的差分格式。
3.基本步骤有限差分法求解偏微分方程的步骤如下：① 区域离散化，即把所给偏微分方程的求解区域细分成由有限个格点组成的网格；② 近似替代，即采用有限差分公式替代每一个格点的导数；③ 逼近求解。
换而言之，这一过程可以看作是用一个插值多项式及其微分来代替偏微分方程的解的过程。
换而言之，这一过程可以看作是用一个插值多项式及其微分来代替偏微分方程的解的过程。
在第一步中，我们通过所谓的网络分割法，将函数定义域分成大量相邻而不重合的子区域。
通常采用的是规则的分割方式。
这样可以便于计算机自动实现和减少计算的复杂性。
网络线划分的交点称为节点。
若与某个节点 P 相邻的节点都是定义在场域内的节点，则 P 点称为正则节点；反之，若节点 P 有处在定义域外的相邻节点，则 P 点称为非正则节点。
在第三步中，数值求解的关键就是要应用适当的计算方法，求得特定问题在所有这些节点上的离散近似值。
差分方程，又叫做差分格式，从格式的精度来划分，有一阶格式、二阶格式和高阶格式；从差分的空间形式来考虑，可分为中心格式和逆风格式；考虑时间因子的影响，差分格式还可以分为显格式、隐格式、显隐交替格式等。
目前常见的差分格式，主要是上述几种形式的组合，不同的组合构成不同的差分格式。
向前差分 (forword difference）：i 1ix x i 1 x i向后差分 (backword difference)：i i 1x x i x i 1中心差分 (cential difference)：i 1i 1x x i 1 x i 1下面以一个例子解释其他差分格式：设求解区域内一个节点A，坐标x j, t n。
根据微商定义和中值定理，把偏微分方程写成差分格式。
对流方程：ua u0(2-1)t x或u t a u x0 可以将其化为三种不同的差分方程：1）时间前差、空间中心差u n j 1 u n j u n j 1 u n j 1a2 0t x或u n j1 r u nj 1 u n j 1 t 1u n j， r a2x2）时间前差、空间前差unj1u nja u nj 1u njtx或u n j 1u n j r u nj 1 u n j3）时间前差、空间后差u n j 1 u n ja u n j u n j 1 0tx或u n j 1u n j r unjunj 1差分方程的时间微商采用前差， 称为显式差分格式； 时间微商采用后差，称为隐式差分格式。
显式差分方程可以直接求解，隐式差分方程需要迭代求解。
除此之外，它还可以构造其他形式的差分格式。
不同的差分格式具有不同的计算精度。
用差分方程代替偏微分方程时必然有误差， 称为截断误差，用 R n j 表示。
差分方程的截断误差等于各项差商逼近微商时所产生误差的总和。
用差分方程的定解条件来代替偏微分方程的定解条件也会产生误差，称为定解条件的截断误差，用 r j n 来表示。
差分方程的截断误差可以用 Taylor 展开法得到。
如上述例子中时间前差、空间中心差分格式，通过 Taylor 展开可得：unj1u n j u n j 1 u n j 1utax t2 n2unu 1tt 2aj2jxn1 3 ux 2 j3！ x 3u a utxn O t, x 2j它的截断误差为： R n j O t , x 2 ，即时间上是一节精度，空间上是二阶精度。
构造差分的方法有多种形式， 直接差分逼近法、 Taylor 级数展开法、控制体积元法和积分方法等。
目前主要采用的是泰勒级数展开方法。
其基本的差分表达式主要有三种形式：一阶向前差分、一阶向后差分、 一阶中心差分和二阶中心差分等， 其中前两种格式为一阶计算精度， 后两种格式为二阶计算精度。
通过对时间和空间这几种不同差分格式的组合，可以组合成不同的差分计算格式。
首先讨论 Taylor 级数展开法：给定任意连续方程u x，对于u xx ，令步长 x h ，可写出 Taylor 级数展开式：u x h u x hu h 22uh 33uh n nuh nnux2! x 23! x 3n!x nn 0n!x n给出有限差分表达式是反过来： 对有限的 x h 给出 u的近似表达式：x记 u j 1 u x x ，由 Taylor 级数表达式可得u表达式xu u x h u x h2 uh 2 3ux h 2! x 2 3! x 3对于上述提到的对流方程 2-1 ，Taylor 展开法是将 u n j 1 在 u n j 点上进行展开，再利用方程把u、22u、3u3变换为 u 、2u 2、tttx x3u 3 ，并把u 、 2u 2、3u 3 用差商表示，就可以得到各种不同 xxxx的差分方程。
对式 2-1 首先将 u n j 1在 u n j 点上进行 Taylor 展开，可得：unj1u jnutn1 2u ntt 2 O t3j2 t 2j（2-2）利用原方程关系：u a u，2u a2 2utxt 2x 2将上式代入式 2-2，得到：n 1n 1n n 12nn nu ju j r u j 1uj 1ruj 12u juj 12 2其中， r at，这就是著名的 Lax-Wendroff 差分方程。
x直接差分逼近法由微商定义：ulim u n j 1u n jttt 0u lim u n j 1 u n jxxx 0和中值定理得到：n 1nn2 ntu ju ju 1 t utt j 2 t 2 j u j n 1 u n ju n1 2u nxxx2x2jjxnnn2n4nu j 12u j u j 1 u 1 x 2 ux 2x 2j12x 4 j x其中， 为 0 1之间的常数。
把这些表达式代入到对流方程式 2-1 中，取一阶近似，并略去 R j n的小量得到相应的差分方程。
如上式可得： unj1u j nu n j 1 u n juan tn t2uuana x 2untxtj2 t2jxj2x 2jx略去等式右边 R n j 项后，得到差分方程：时间前差、空间前差：u n j 1 u n j r u n j 1u n j其中， r at。
采用相同的差分逼近法，也可以得到其它差分方程。
x例如：时间前差、空间后差：时间前差、空间中心差：积分方法u n j 1 u n j r u n j u n j 1u n j 1 u n j1r u n j 1 u n j 12计分方法是把偏微分方程在一定的控制体内进行积分，得到相应的差分方程。
以对流方程 2-1 为例，在矩形网格的控制体单元d内，对时间和空间取前差，并从 t n到 t n t ，从 x j到 x j x 进行积分：u t au x dxdt 0通过积分运算：x j x t n t t n t x j xx j t n u t dtdx a t n x j u x dxdt 0 则得到 ;x j xu n t ntu n 1 dx a n u j 1 u j dt 0x j t把上式用数值积分近似表示，整理后可得：u n j1u n j r u n j 1u n j其中， r a t 。
x差分方程的有效性分析一个偏微分方程可以得到不同的差分方程。
