当前位置：文档之家 › 隐性有限差分方法显性有限差分方法

隐性有限差分方法显性有限差分方法

  • 格式：ppt
  • 大小：1.57 MB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

显性差分法

显性差分法

一、欧式看涨期权的显性差分clearS0 = 50;K = 50;r = 0.1;T = 12;sigma = 0.2;Smax = 100;dS=1;dt=0.001;%建立网格，并且在必要时调整增量M=round(Smax/dS);dS=Smax/M;N=round(T/dt);dt=T/N;matval=zeros(M+1,N+1);vetS=linspace(0,Smax,M+1);veti=0:M;vetj=0:N;%建立边界条件matval(:,N+1)=max(vetS-K,0); % 在时间到期时的期权价格matval(1,:)=0; %在S=0时的期权价格matval(M+1,:)=dS*M-K*exp(-r*dt*(N-vetj)); %在S=Smax时的期权价格%建立三对角矩阵a=0.5*dt*(sigma^2*veti-r).*veti;b=1-dt*(sigma^2*veti.^2+r);c=0.5*dt*(sigma^2*veti+r).*veti;%求解方程for j=N:-1:1for i=2:Mmatval(i,j)=a(i)*matval(i-1,j+1)+b(i)*matval(i,j+1)+c(i)*matval(i+1,j+1);endend %返回价格，有可能在网格外线性插值生成price=interp1(vetS,matval(:,1),S0)二、欧式看跌期权的显性差分clearS0 = 50;K = 50;r = 0.01;T = 12;sigma = 0.2;Smax = 100;dS=2;dt=0.01;%建立网格，并且在必要时调整增量M=round(Smax/dS);dS=Smax/M;N=round(T/dt);dt=T/N;matval=zeros(M+1,N+1);vetS=linspace(0,Smax,M+1);veti=0:M;vetj=0:N;%建立边界条件matval(:,N+1)=max(K-vetS,0);matval(1,:)=K*exp(-r*dt*(N-vetj));matval(M+1,:)=0;%建立三对角矩阵a=0.5*dt*(sigma^2*veti-r).*veti;b=1-dt*(sigma^2*veti.^2+r);c=0.5*dt*(sigma^2*veti+r).*veti;%求解方程for j=N:-1:1for i=2:Mmatval(i,j)=a(i)*matval(i-1,j+1)+b(i)*matval(i,j+1)+c(i)*matval(i+1,j+1);endend %返回价格，有可能在网格外线性插值生成price=interp1(vetS,matval(:,1),S0)。

3第二章-有限差分方法基础

3第二章-有限差分方法基础

2.1.1 基本方程和定解问题
u t
2u x2
( 0)
求解域： (x, t) [0,1][0, ]
(2.1.1)
初始条件： u(x, 0) f (x)
边界条件： u(0, t) a(t), u(1, t) b(t)
(2.1.2)
方程(2.1.1)和初边条件(2.1.2)构成了一个适定的定解问题。
根据数学分析中的知识，我们知道
2u (x,t) lim u(x x,t) 2u(x,t) u(x x,t)
x2
x0
x2
所以，二阶导数可以近似为
2u
x
2
n
k
un k 1
2ukn x2
ukn
un k 1
2ukn
un k 1
称为二阶中心差分。
容易证明：
un k 1
2ukn
un k 1
t
)
ut
(
x,
t
)
lim
t 0
u(
x,
t
t
)u 2t
(
x,
t
t
)
其中，lim 后面的项称为差商(difference quotient)。 t 0
当t足够小时，可以用差商来近似导数。
即：
u(x,t t) u(x,t)
ut (x,t)
t
u(x,t) u(x,t t)
ut (x,t)
t
u(x,t t) u(x,t t)
The Elements of Computational Fluid Dynamics
第二章 有限差分方法基础
§2.1 有限差分方法概述 §2.2 导数的数值逼近方法 §2.3 差分格式的性质 §2.4 发展方程的稳定性分析

期权定价的数值方法

期权定价的数值方法

期权定价的数值方法小结1.当不存在解析解时，可以用不同的数值方法为期权定价，其中主要包括二叉树图方法、蒙特卡罗模拟和有限差分方法。

2.二叉树图方法用离散的随机游走模型模拟资产价格的连续运动在风险中性世界中可能遵循的路径，每个小的时间间隔中的上升下降概率和幅度均满足风险中性原理。

从二叉树图的末端开始倒推可以计算出期权价格。

3.蒙特卡罗方法的实质是模拟标的资产价格在风险中性世界中的随机运动，预测期权的平均回报，并由此得到期权价格的一个概率解。

4.有限差分方法将标的变量满足的偏微分方程转化成差分方程来求解，具体的方法包括隐性有限差分法、显性有限差分法、“跳格子方法”和Crank-Nicolson方法等。

5.树图方法和有限差分方法在概念上是相当类似的，它们都可以看成用离散化过程解出偏微分方程的数值方法，都适用于具有提前执行特征的期权，不太适合路径依赖型的期权。

其中二叉树模型由于其简单直观和容易实现，是金融界中应用得最广泛的数值定价方法之一；有限差分方法则日益受到人们的重视。

6.蒙特卡罗方法的优点在于应用起来相当直接，能处理许多盈亏状态很复杂的情况，尤其是路径依赖期权和标的变量超过三个的期权，但是不擅长于处理美式期权，而且往往所需计算时间较长。

二叉树定价方法的基本思想：假设资产价格的运动是由大量的小幅度二值运动构成，用离散的随机游走模型模拟资产价格连续运行可能遵循的路径。

模型中隐含导出的概率是风险中性世界中的概率p，从而为期权定价。

蒙特卡洛模拟的基本思想：由于大部分期权的价值都可以归结为期权到期回报的期望值的贴现，因此尽可能地模拟风险中性世界中标的资产价格的多种运动路径，计算每种结果路径下的期权回报均值，之后贴现就可以得到期权价值。

蒙特卡洛模拟的优点：在大多数情况下，人们可以很直接地应用蒙特卡洛模拟，而无需对期权定价模型有深刻的认识；蒙特卡洛模拟的适用情形相当广泛。

蒙特卡洛模拟的缺点：只能为欧式期权定价，难以处理提前执行期权的的定价情形；为了达到一定的精准度，需要大量的模拟运算。

CAN 总线规范

CAN 总线规范

CAN 总线规范CAN总线属于现场总线的范畴，它是一种有效支持分布式控制或实时控制的串行通信网络，位速率可高达1MBPS。

可以应用在汽车控制系统，自动化电子领域中的各种部件（传感器，灯光，执行机构等）与主机连接组成CAN 网络。

本章介绍通过CAN总线与液晶显示器的连接。

CAN 具有下列主要特性：1 多主站依据优先权进行总线访问。

总线开放时，任何单元均可开始发送报文，具有最高优先权的报文的单元赢得总线访问权。

利用这个特点可以用液晶显示器作为多主机的公用监视器，不用每台主机配一个监视器，从而节约系统成本。

2 无破坏性的基于优先权的仲裁。

网络上的每个主机可以同时发送，哪个主机的数据可以发送出去取决于主机所发送报文的标识符决定的优先权的大小，没有发送出去的帧可自动重发。

以后将介绍数据怎样仲裁。

3 借助接收滤波的多地址帧传送收到报文的标识符与本机的接收码寄存器与屏蔽寄存器相比较，符合的报文本机才予以接收。

4．远程数据请求。

网络上的每个接点可以发送一个远程帧给另一个接点，请求该接点的数据帧，该数据帧与对应的远程帧以相同的标识符ID命名。

5．配置灵活性通过八个寄存器进行接点配置，每个接点可以接收，也可以发送。

6．全系统数据相容性7．错误检测和出错信令有五种错误类型，每个接点都设置有一个发送出错计数器和一个接收出错计数器。

发送接点和接收接点在检测到错误时，出错计数器根据一定规则进行加减，并根据错误计数器数值发送错误标志（活动错误标志和认可错误标志），当错误计数器数值大于255时，该接点变为“脱离总线”状态，输出输入引脚浮空，既不发送，也不接收。

CAN 中的总线数值为两种互补逻辑数值：“显形”和“隐性”，用差分电压表示。

“显形”表示逻辑“0”，显性状态用大于最小阈值的差分电压表示。

“隐性”表示逻辑“1”，这时输出的差分电压Vdiff 近似为0，Vcanh ，Vcanl固定于平均电压电平，显性位与隐性位同时发送时，最后总线数值为显性。

隐性有限差分方法显性有限差分方法

隐性有限差分方法显性有限差分方法
19
随机路径： 在风险中性世界中， 为了模拟路径 dS r q Sdt Sdz ，我们把期权的有效期 分为N个长度为时间段，则上式的近似方程为
2 ln S t t ln S t r q t t 2
或
r q t 2 ue
2
，
r q t t 2 d e 该方法优点在于无论 和 t 如何变化，概率总是不
2
d
t
2
2
变的
13
三叉树图
每一个时间间隔 t 内证券价格有三种运动的可能： 1、从开始的 S 上升到原先的 u 倍，即到达 Su ； 2、保持不变，仍为 S ； 3、下降到原先的 d 倍，即 Sd
Su2 Su S S Sd Su S Sd
Su3 Su2 Su S Sd Sd2 Sd3
Sd2
14
一些相关参数：
ue
1 d u
3t
t pd 12 2
2 1 r q 2 6
t pu 12 2
2 1 r q 2 6
际上是在用大量离散
的小幅度二值运动来 模拟连续的资产价格
相同期 限下步 长越小
精确度 越高
运动
3
无套利定价法： 构造投资组合包括 份股票多头和1份看涨期权空头 fd 当 Su u Sd 时 ,股票价格的变动对组合无影响则组合为无风险组合
此时
fu f d Su Sd
A
则期权A 的更优估计值为：
f A fˆA f B fˆB
16
适应性网状模型
在使用三叉树图为美式期权定价时，当资产价格接近执行价
格时和接近到期时，用高密度的树图来取代原先低密度的树图。 即在树图中那些提前执行可能性较大的部分，将一个时间步 长

热传导方程有限差分法的MATLAB实现

热传导方程有限差分法的MATLAB实现

万方数据万方数据万方数据万方数据热传导方程有限差分法的MATLAB实现作者：史策作者单位：西安建筑科技大学,理学院,陕西,西安,710055刊名：咸阳师范学院学报英文刊名：JOURNAL OF XIANYANG NORMAL UNIVERSITY年，卷(期)：2009，24(4)被引用次数：0次1.曹钢,王桂珍,任晓荣.一维热传导方程的基本解[J].山东轻工业学院学报,2005,19(4):76-80.2.万正苏,方春华,张再云.关于热传导方程有限差分区域分解并行算法精度的注记[J].湖南理工学院学报(自然科学版),2007,20(3):12-14.3.StephenJ.Chapman.MATLAB编程[M].邢树军,郑碧波,译.北京:科学出版社,2008.4.田兵.用MATLAB解偏微分方程[J].阴山学刊,2006,20(4):12-13.5.王飞,裴永祥.有限差分方法的MATLAB编程[J].新疆师范大学学报(自然科学版),2003,22(4):21-27.6.王宝红.热传导方程的可视化探讨[J].忻州师范学院学报,2008,24(2):31-36.7.李先枝.热传导方程差分解法的最佳网格[J].河南大学学报(自然科学版),2004,34(3):16-18.8.赵德奎,刘勇.MATLAB在有限差分数值计算中的应用[J].四川理工学院学报,2005,18(4):61-64.9.谢焕田,吴艳.拉普拉斯有限差分法的MATLAB实现[J].四川理工学院学报,2008,21(3):1-2.10.南京大学数学系计算数学专业.偏微分方程数值解法[M].北京:科学出版社,1979.1.学位论文申卫东热传导方程有限差分区域分解算法研究2003区域分解算法是在并行机上求解偏微分方程数值解的一种较自然的方法.该方法先将偏微分方程求解区域划分为若干个子区域,然后在各个子区域并行求解.全文共五章.第一章为引言,简要介绍了热传导方程并行算法的概况及该文所讨论的基本内容.在第二章,我们在内边界点为等距分划的多子区域条件下,得到Dawson等人关于求解热传导方程区域分解算法差分解的误差估计.在第三章,我们以Saul'yev非对称格式作内边界处理,发展了新的区域分解算法,得到了差分解的先验误差估计,并与Dawson等人的算法作了比较.给出了关于算法计算精度的数值结果.在第四章,我们发展了一些新技术,在子区域的边界处采用小时间步长古典显式格式求解,构造了新的区域分解算法,得到了差分解的先验误差估计.给出了关于算法计算精度的数值结果.在第五章,我们在二维热传导方程求解上扩充了Dawson等人的区域分解算法.给出了关于算法计算精度的数值结果.第六章为该研究工作的主要结论.2.期刊论文张守慧.王文洽.ZHANG Shou-hui.WANG Wen-qia热传导方程有限差分逼近的数学Stencil及其新型迭代格式-山东大学学报（理学版）2006,41(6)将Stencil应用于偏微分方程有限元差分逼近过程,以两类差分格式为基础建立了求解热传导方程的两种新型迭代算法.此两种算法与经典的Jacobi方法同样具有并行的性质,但比Jacobi方法收敛快.给出的算例说明方法的适用性.3.期刊论文吕桂霞.马富明.Lü Guixia.Ma Fuming二维热传导方程有限差分区域分解算法-数值计算与计算机应用2006,27(2)本文讨论了一类数值求解二维热传导方程的并行差分格式.在这个算法中,通过引进内界点将求解区域分裂成若干子区域.在子区域间内界点上采用非对称格式计算,一旦这些点的值被计算出来,各子区域间的计算可完全并行.本文得到了稳定性条件和最大模误差估计.它表明我们的格式有令人满意的稳定性,并且有着较高的收敛阶.4.学位论文田源地下煤火三维数理模型正演数值模拟2006本文首先给出了几个地下煤火随空间、温度变化的动态和稳态热数学物理模型及其简化模型。

第四章离散化的基本方法


u ( x )i, j

ui1, j ui1, j 2x
O(x)2
(6)
二阶“中心差分”
总结：
ui1, j ui, j

x
O(x)
一阶“向前差分”
u ( x )i, j


ui
,
j

ui1, j x
O(x)
一阶“向后差分”
ui1, j ui1, j
x
x2 2
最初的估计 斜率的影响 曲率的影响
举例说明
8
Nanjing University of Technology
有限差分基础
考虑函数 f (x) sin 2 x
在x＝0.2处，f(x)＝0.9511。如图中1点。
取Δx＝0.02，f(x+Δx)=f(0.22)=0.9823 图中点2
)i
,
j
(x)

(
2u x2
)i
,
j
(x)2 2

(
3u x3
)i
,
j
(x)3 6

(4)
解得：
(
u x
)i
,
j

ui, j
ui1, j x
O(x) (5)
一阶“向后差分”
11
Nanjing University of Technology
有限差分基础
对于CFD而言，一阶精度是不够的。为构造2阶精度。直接 用（2）式减去（4）式得到：
ui2, j
O(x)4
越高精度在计算过程中是不是就越好呢？
缺点：需要更多的网格信息，所以计算每一步时间步 或者空间步需要更多时间。

解读CANDT测试项“总线输入电压限值测试”

解读CANDT测试项“总线输入电压限值测试”摘要：为了保证CAN总线物理层的一致性，CANDT系统参考ISO11898-2标准及主流车企标准对CAN节点相关的参数进行测量，本文主要对CANDT的测试项—总线输入电压限值测试进行解读。

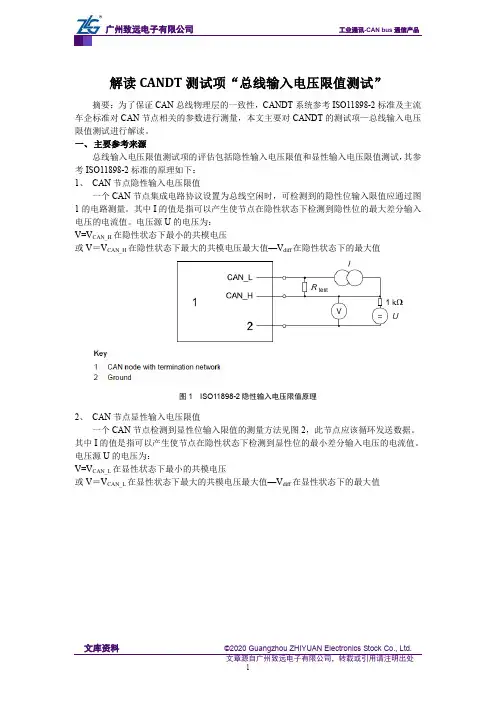
一、主要参考来源总线输入电压限值测试项的评估包括隐性输入电压限值和显性输入电压限值测试，其参考ISO11898-2标准的原理如下：1、CAN节点隐性输入电压限值一个CAN节点集成电路协议设置为总线空闲时，可检测到的隐性位输入限值应通过图1的电路测量。

其中I的值是指可以产生使节点在隐性状态下检测到隐性位的最大差分输入电压的电流值。

电压源U的电压为：V=V CAN_H在隐性状态下最小的共模电压或V＝V CAN_H在隐性状态下最大的共模电压最大值—V diff在隐性状态下的最大值图1 ISO11898-2隐性输入电压限值原理2、CAN节点显性输入电压限值一个CAN节点检测到显性位输入限值的测量方法见图2，此节点应该循环发送数据。

其中I的值是指可以产生使节点在隐性状态下检测到显性位的最小差分输入电压的电流值。

电压源U的电压为：V=V CAN_L在显性状态下最小的共模电压或V＝V CAN_L在显性状态下最大的共模电压最大值—V diff在显性状态下的最大值图2 ISO11898-2显性输入电压限值原理二、CANDT测试原理CAN总线输入电压限值即DUT接收报文过程中能正常识别的差分电压范围，按照ISO11898-2的定义，隐性电平上限值为0.5V，当总线出现等于0.5V的差分电平时，DUT 应能正确识别为隐性状态而正常发送报文；显性电平的下限值为0.9V，当总线出现等于0.9V 的差分电平时，DUT应能正确识别为显性电平状态而停止发送报文。

即使总线存在一定范围内的共模干扰，也能正确进行以上识别。

CANDT测试原理框图如图3、图4所示，其中框图中的U1是DUT供电电压、U2是共模电压、U3是差分电平。

VTI介质隐式有限差分平面波偏移


在减 少计 算量 ， 高 波 动 方 程偏 移 效 率 上 的 潜 力 。 提 Ｂｒｈｕ¨提 出面炮 偏 移 技术 ； ｅｋｏｔ 张叔 伦 等 实 现 了
傅立 叶有 限差 分 平 面 波 偏 移 ； ｈ ｎ Ｚ ａｇ等 实 现 ３ Ｄ
关 系要 复杂 些 ， 因为其 传播 速 度依赖 于相 位角 。所 以 ， Ｖ Ｉ 质 波 场 外 推 经 常 使 用 相 移 加 内插 ¨ 在 Ｔ介
向 同性 介质 下 ， 有考 虑 各 向异 性介 质情 况 。而 各 没
向异 性 在石 油勘探 中普 遍 存在 ， 如果 地 下介质 存 在
求解 差 分 系数 。作者 在本 文延 用 Ｓａ 开弱 各 向 ｈｎ避
异性 假 设及 优化 的思 想 ， 同的是 作者直 接建 立非 不
基 金 项 目：国 家“ ７ ” 目（ ０ ７ Ｂ ０ ６ ３ ； ９３ 项 ２ ０ Ｃ ２ ９ ０ ） 国家 ８ ３项 目（ ０ ７ Ａ ６ ８ １ ６ ２０Ａ ０００ ）
或 显性 卷 积 方 法 ¨ ， 因为 复 杂 的频 散 关 系 并 不 增 加这 些方 法 的复 杂性 。但 是对 于相 移加 内插 法 ， 需 要大 量 的参 考 波 场 。显 性 卷 积 方法 在 各 向 同性 下 都很 难保 证稳 定性 ， 而且需 要很 长 的卷积 滤波算
延 迟 放炮 偏 移 ；ｔ ａ等 对 共 检 波点 道 集 和 共 炮 Ｓｏ ｆ
ｅｃ ：ＩＤ） 法 。Ｒｓ ｗ等 ¨ ｎｅ Ｆ 算 ｉｏ ｔ 基 于弱 各 向 异性 假 设 和 Ｔｙ ｒ 析 将 其 拓 展 到 Ｖ Ｉ 质 。为 了改 ａｌ 分 ｏ Ｔ介 善精度 ，ｉ Ｈ 有 限差 分后加 人 了相 位 改正 算 Ｌｕ等 在
子 。Ｓ ａ ¨ 提 出 了优 化 的方 法 ， 非 线 性 问 题 ｈｎ 将 降解 为线性 优化 问题 ， 利用 线性 优 化解 出的 系数 再

金融工程-完整版

考试形式-12个题目选10个答~只改10个~多答无效~这个复习文档是武媚整理的...强烈感谢哦~我只负责录入-_-||| ...-------------------------------------------------------------------------------------------------------------------- 1.金融工程的定义是什么？金融工程是做什么的？金融工程：包括设计、开发和实施具有创新意义的金融工具和金融手段，并且对金融问题提出创造性的解决方案。

工程化地解决金融问题：定量化、可重复、标准化。

经济环境的变化：金融创新的推动，信息技术的发展史金融工程发展的外部条件，市场参与者追求市场效率是金融工程产生的内在动因。

风险管理在金融工程中居于核心地位。

现在金融理论的发展是金融工程产生的思想基础，金融工程活动反过来又为金融理论的进一步创新提供了实践的舞台。

2.金融工程的分析方法？核心？无套利工具分析？投资组合？未来收益相等现在价值相等，一价定理，复制。

模拟-》积木分析。

（1）金融工程的核心思想：无套利定价法。

套利是在某项金融资产的交易过程中，交易者可以在不需要期初投资支出的条件下获取无风险报酬。

无套利定价方法：一价律，若两种资产（组合）的期末价值相同，则期初的价值也相同。

无套利定价法的基本思路为：构建两种投资组合，让其终值相等，则其现值一定相等；否则就可以进行套利，即卖出现值较高的投资组合，买入现值较低的投资组合，并持有到期末，套利者就可赚取无风险收益。

众多套利者这样做的结果，将使较高现值的投资组合价格下降，而较低现值的投资组合价格上升，直至套利机会消失，此时两种组合的现值相等。

这样，我们就可根据两种组合现值相等的关系求出远期价格。

无套利定价的机制的主要特征：1）要求套利活动在无风险的状态下进行2）无套利定价的关键技术就是所谓的“复制”技术，即用一组证券来复制另外一组证券3）无风险的套利活动从即时现金流看是零风险投资组合。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

因为是无风险组合，可用无风险利率贴现，得
S f Su fu ert
将
fu f d Su Sd
代入上式就可得到：
f e r t pf u 1 p f d
其中
e rt d p ud
4
在风险中性世界里： （1）所有可交易证券的期望收益都是无风险利率； （2）未来现金流可以用其期望值按无风险利率贴现。在风险中性的条件下, 参数值满足条件：
Rubinstein所用的条件） 由以上三式可得，当
t 很小时：
p
e rt d ud
u e
t
d e tFra bibliotek从而 f e r t pf u 1 p f d 以上可知，无套利定价法和风险中性定价法具有内在一致性。
5
倒推定价法
得到每个结点的资产价格之后，就可以在二叉树模型中采用倒推定价 法，从树型结构图的末端T时刻开始往回倒推，为期权定价。 如果是欧式期权，可通过将 T 时刻的期权价值的预期值在 t 时间 长度内以无风险利率 r 贴现求出每一结点上的期权价值；
7
当标的资产支付连续收益率为
q 的红利时，在风险中性条件下，证券价格的增长率应该为，
r q 因此：
e ( r q) t pu (1 p)d
e ( r q ) t d p ud
对于股价指数期权来说， q 为股票组合的红利收益 率；对于外汇期来说， q 为国外无风险利率，因此 以上式子可用于股价指数和外汇的美式期权定价。
际上是在用大量离散
的小幅度二值运动来 模拟连续的资产价格
相同期 限下步 长越小
精确度 越高
运动
3
无套利定价法： 构造投资组合包括 份股票多头和1份看涨期权空头 fd 当 Su u Sd 时 ,股票价格的变动对组合无影响则组合为无风险组合
此时
fu f d Su Sd
,N 可得：f N，j max( X Su j d N j ,0)，其中 j 0,1, rt 若期权不被提前执行， t 后，则：fij e [ pfi1, j 1 (1 p) fi1, j ] 所以 fij (0 i N ,0 j i) 实际上表示在时间 it 时第j个结点处的 美式看跌期权的价值 若有提前执行的可能性，则 fij max{X Su j d i j , ert [ pfi1, j 1 (1 p) fi1, j ]} 这样推至 f 00 即为当前期权的价格。
假设在期权有效期内只有一次红利，除息日在0到τ之间，则在iΔt时刻不确定部分的价值为： 当 it 时 S * (it ) S (it ) 当 it 时（表示红利） S * (it ) S (it ) De r ( it ) 综上可得在 i t 时刻： 当 i t 时，这个树上每个结点对应的证券价格为： S0*u j d i j Der ( it ) 当 it 时，这个树上每个结点对应的证券价格为：
如果是美式期权，就要在树型结构的每一个结点上，比较在本时刻提 前执行期权和继续再持有 t 时间，到下一个时刻再执行期权，选择其中 较大者作为本结点的期权价值。（见书本案例 12.1）
6
二叉树一般定价过程 假设把该期权有效期划分成N个长度为 t 的小区间，同时用 Su j d i j 表示结点 (i, j ) 处的证券价格
j 0,1,
u e
t
d e
t
8
可通过调整在各个结点上的证券价格，算出期权价格；
如果时刻 i t 在除权日之前，则结点处证券价格仍为： Su j d i j , j 0,1, , i 如果时刻i t 在除权日之后，则结点处证券价格相应调整为：
S (1 )u j d i j j 0,1,
在第十一章中，我们得到了期权价值所满足的偏微分 方程，并解出了特定条件下的期权解析定价公式。但在很多情 形中，我们无法得到期权价值的解析解，这时人们经常采用数 值方法（Numerical Procedures）为期权定价，主要包括二叉 树方法（Binomial Trees）、蒙特卡罗模拟（Monte Carlo Simulation）和有限差分方法（Finite Difference Methods）。在这一章里，我们将介绍如何借助上述三种数值 方法来为期权定价。为了便于表达，本章中统一假设当前时刻 为零时刻。
,i
时刻结点的相应的证券价
若在期权有效期内有多个已知红利率，则 i t 格为： S (1 )u j d i j
i
（
i
为0时刻到 i t 时刻之间所有除权日的总红利支付率）
9
如何解决节 点不重合的问 题
Su S S-D Sd Sd2-D 除权日 Su2-D
10
在已知红利额的情况下,为了使得二叉树的节点重合减少计算量,我 们可以将证券价格分为两个部分：一部分是不确定的；另一部分是期权 有效期内所有未来红利的现值。
Sert pSu (1 p)Sd e rt pu (1 p)d
假设证券价格遵循几何布朗运动，则：
S 2 2 t pS 2 u 2 (1 p)S 2 d 2 S 2 [ pu (1 p)d ] 2
2 t pu 2 (1 p)d 2 pu (1 p)d 2 1 再设定： u （第三个条件的设定则可以有所不同， 这是Cox、Ross和 d
1
把期权的有效期分为很多很小的时间间 隔 t ，并假设在每一个时间间隔 t 内证 券价格只有两种运动的可能：
Su p S 1-p Sd
1、从开始的 S 上升到原先的
u 倍，即到达 Su
；
2、下降到原先的 d 倍，即 Sd 相应地，期权价值也会有所不同，分 别为 fu 和 fd 。
2
二叉树模型的思想实