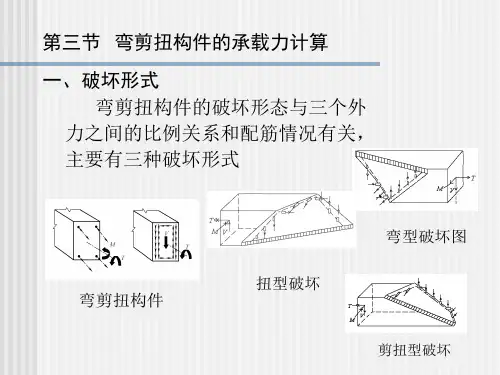
钢筋混凝土弯剪扭构件承载力计算

混凝土结构扭曲截面承载力计算1、在弯矩、剪力和扭矩共同作用下，h w/b不大于6的矩形、T形、I形截面和h w /t w不大于6的箱形截面构件（图6.4.1），其截面应符合下列条件：当h w/b（或h w/t w）不大于4时当h w/b（或h w/t w）大于4但小于6时，按线性内插法确定。

式中：T——扭矩设计值；b——矩形截面的宽度，T形或I形截面取腹板宽度，箱形截面取两侧壁总厚度2t w；W t——受扭构件的截面受扭塑性抵抗矩，按本规范第6.4.3条的规定计算；h w——截面的腹板高度：对矩形截面，取有效高度h0；对T形截面，取有效高度减去翼缘高度；对I形和箱形截面，取腹板净高；t w——箱形截面壁厚，其值不应小于b h/7，此处，b h为箱形截面的宽度。

注：当h w/b大于6或h w/t w大于6时，受扭构件的截面尺寸要求及扭曲截面承载力计算应符合专门规定。

2、在弯矩、剪力和扭矩共同作用下的构件，当符合下列要求时，可不进行构件受剪扭承载力计算，但应按本规范第9.2.5条、第9.2.9条和第9.2.10条的规定配置构造纵向钢筋和箍筋。

3、受扭构件的截面受扭塑性抵抗矩可按下列规定计算：1 矩形截面2 T形和I形截面3 箱形截面4、矩形截面纯扭构件的受扭承载力应符合下列规定：式中：ζ——受扭的纵向普通钢筋与箍筋的配筋强度比值，ζ值不应小于0.6，当ζ大于1.7时，取1.7；A stl——受扭计算中取对称布置的全部纵向普通钢筋截面面积；A st1——受扭计算中沿截面周边配置的箍筋单肢截面面积；f yv——受扭箍筋的抗拉强度设计值，按本规范第4.2.3条采用；A cor——截面核心部分的面积，取为b cor h cor，此处，b cor、h cor分别为箍筋内表面范围内截面核心部分的短边、长边尺寸；u cor——截面核心部分的周长，取2（b cor＋h cor）。

注：当ζ小于1.7或e p0大于h/6时，不应考虑预加力影响项，而应按钢筋混凝土纯扭构件计算。

第三章钢筋混凝土受弯构件正截面承载力计算第三章钢筋混凝土受弯构件正截面承载力计算第三章钢筋混凝土受弯构件正截面承载力计算第一节钢筋砼受弯构件的构造一、钢筋砼板的构造二、钢筋砼梁的构造一、钢筋砼板(reinforced concreteslabs)的构造1、钢筋砼板的分类：整体现浇板、预制装配式板。

2、截面形式小跨径一般为实心矩形截面。

跨径较大时常做成空心板。

如图所示。

3、板的厚度：根据跨径(span)内最大弯矩和构造要求确定，其最小厚度应有所限制：行车道板一般不小于100mm；人行道板不宜小于60mm(预制板)和80mm(现浇筑整体板)。

4、板的钢筋由主钢筋(即受力钢筋)和分布钢筋组成如图。

钢筋混凝土板桥构造图（1）主筋布置：布置在板的受拉区。

直径：行车道板：不小于10mm；人行道板：不小于8mm。

间距：间距不应大于200mm。

主钢筋间横向净距和层与层之间的竖向净距，当钢筋为三层及以下时，不应小于30mm，并不小于钢筋直径；当钢筋为三层以上时，不应小于40mm，并不小于钢筋直径的1.25倍。

净保护层：保护层厚度应符合下表规定。

序号构件类别环境条件ⅠⅡⅢ、Ⅳ1 基础、桩基承台⑴基坑底面有垫层或侧面有模板（受力钢筋）⑵基坑底面无垫层或侧面无模板465756852 墩台身、挡土结构、涵洞、梁、板、拱圈、拱上建筑（受力主筋）34453 人行道构件、栏杆（受力主筋）22534 箍筋22535 缘石、中央分隔带、护栏等行车道构件34456 收缩、温度、分布、防裂等表层钢筋15225梁构件，在不同环境条件下，保护层厚度值注：请点击<按扭Ⅰ,Ⅱ,Ⅲ&Ⅳ>，以查看不同保护层厚度值（2）分布钢筋(distribution steel bars)：垂直于板内主钢筋方向上布置的构造钢筋称为分布钢筋作用：A、将板面上荷载更均匀地传递给主钢筋B、固定主钢筋的位置C、抵抗温度应力和混凝土收缩应力(shrinkage stress)布置：A、在所有主钢筋的弯折处，均应设置分布钢筋B、与主筋垂直C、设在主筋的内侧数量：截面面积不小于板截面面积的0.1%。

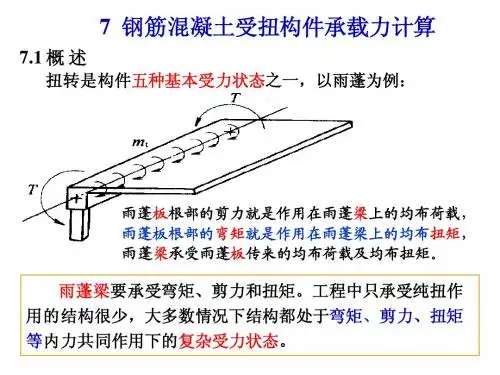
钢筋混凝土受扭构件承载力设计计算摘要：结合桥梁设计工作实践经验论述了受扭构件承载力的计算方法和计算公式，结合具体实例，提出了钢筋混凝土受扭构件设计及承载力的计算方法及适用范围，以供设计者参考借鉴。

关键词：桥梁工程桥梁构件混凝土受扭构件承载力设计内力计算桥梁工程中扭转构件其受力的基本形式之一，钢筋混凝土结构中常见的构件形式，例如现浇框架边梁或折梁等结构构件都是受扭构件。

受扭构件根据截面上存在的内力情况可分为纯扭、剪扭、弯扭、弯剪扭等多种受力情况。

在实际工程中，纯扭、剪扭、弯扭的受力情况较少，弯剪扭的受力情况则较普遍。

因此，在桥梁结构设计工作中构件的内力计算至关重要。

1 钢筋混凝土矩形截面纯扭构件的设计与计算（1）开裂扭矩的计算：纯扭构件的扭曲截面承载力计算中，首先需要计算构件的开裂扭矩。

如果扭矩大于构件的开裂扭矩，则还要按计算配置受扭纵筋和箍筋，以满足构件的承载力要求。

否则，应按构造要求配置受扭钢筋。

在《公路钢筋混凝土及应力混凝土桥涵设计规范》(JTG D62-2004)中规定，钢筋混凝土矩形截面纯扭构件的开裂扭矩可用公式计算：2 钢筋混凝土弯、剪、扭构件的配筋设计与计算在《公路钢筋混凝土及应力混凝土桥涵设计规范》(JTG D62-2004)中规定，弯、剪、扭构件的配筋计算，也采取叠加计算的截面设计简化方法。

（1）受剪扭的构件承载力计算：现行设计规范中规定，钢筋混凝土剪扭构件的承载能力，一般按受扭和受剪构件分别计算承载能力，然后再它们叠加起来。

但是，剪、扭共同作用的构件，剪力和扭矩对混凝土和箍筋的承载能力均有一定影响。

如果采取简单地叠加，对箍筋和混凝土尤其是混凝土是偏于不安全的。

构件在剪扭的共同作用下，其截面的某一受压区内承受剪切和扭转应力的双重作用，这不仅会降低构件内混凝土的抗剪和抗扭能力，而且分别小于单独受剪和受扭时相应的承载能力。

由于受扭钢筋混凝土构件的受力情况比较复杂，所以对箍筋所承担的承载能力采取简单叠加，混凝土的抗扭和抗剪承载能力考虑其相互影响，在混凝土的抗扭承载能力计算式中，应引入剪扭构件混凝土承载能力的降低系数。

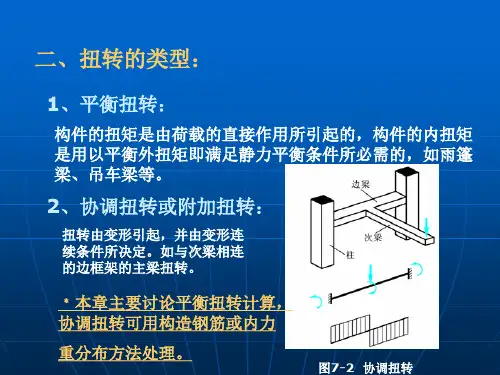
在轴力、弯矩、剪力和扭矩共同作用下,钢筋混凝土矩形截面框架柱的受剪承载力计算1. 引言1.1 概述本文主要研究在轴力、弯矩、剪力和扭矩共同作用下，钢筋混凝土矩形截面框架柱的受剪承载力计算。

钢筋混凝土结构中的柱是承受垂直荷载和水平荷载的重要组成部分，其稳定性和强度对于保证整个结构的安全性至关重要。

在实际工程中，柱往往同时承受着多种力的作用，包括轴向荷载、弯矩、剪力和扭矩等。

这些力的不同组合将显著影响柱的受剪承载能力。

因此，深入了解并准确计算柱在这些作用下的受剪承载能力对于工程设计和评估具有重要意义。

1.2 文章结构本文共分为五个部分进行探讨。

首先，引言部分提供了关于本文内容的概览，并介绍了文章的目标与意义。

接下来，在第二部分中，我们将详细讨论轴力和弯矩对柱受剪承载能力的影响，并介绍受剪承载力的计算方法。

第三部分将重点探讨剪力对柱的影响，包括引起和传递机制，并介绍了针对剪力下柱承载能力计算的方法。

紧接着，第四部分将深入研究扭矩对柱的影响，并详细介绍了扭矩-剪力交互作用下的受剪承载能力计算方法。

最后，我们将在第五部分总结主要结果并提出对未来工作的建议。

1.3 目的本文旨在通过系统地研究轴力、弯矩、剪力和扭矩共同作用下钢筋混凝土矩形截面框架柱受剪承载能力的计算方法，进一步提高人们对于柱结构性能的理解。

这对于设计师在进行柱结构设计时提供了更准确和可靠的依据，并有助于将柱设备应用于各种工程项目中。

此外，在本文中还将探讨可能存在的问题和不足之处，并提出未来研究方向上可以进一步改进与拓展这个领域的建议。

2. 轴力和弯矩对柱的影响2.1 轴力的作用轴力是指柱子上的拉力或压力，它是由外部荷载在垂直于柱子轴线方向施加引起的。

当柱子受到轴向拉力时，称为正轴向拉力；当柱子受到轴向压力时，称为正轴向压力。

轴力会对矩形截面框架柱的承载能力产生显著影响。

2.2 弯矩的作用弯矩是指在柱子上施加偏离中性轴线位置产生的扭曲效应。

通常情况下，外部荷载施加给柱子会引起弯曲变形，从而产生弯矩。

第7章 钢筋混凝土受扭构件承载力计算1．简述钢筋混凝土矩形截面纯扭构件的四种破坏形态及其与设计的关系。

答：矩形截面纯扭构件的破坏形态以下四种类型：（1）少筋破坏当抗扭钢筋数量过少时，裂缝首先出现在截面长边中点处，并迅速沿45°方向向邻近两个短边的面上发展，在第四个面上出现裂缝后（压区很小），构件立即破坏。

破坏形态如图7-3(a)，其破坏类似于受弯构件的少筋梁，破坏时扭转角较小（图7-4曲线1），属于脆性破坏，构件受扭极限承载力取决于混凝土抗拉强度和截面尺寸，设计中应予避免。

该类破坏模型是计算混凝土开裂扭矩的试验依据，并可按此求得抗扭钢筋数量的最小值。

（2）适筋破坏 当抗扭钢筋数量适中时，破坏形态如图7-3(b)。

混凝土开裂并退出工作，由其承担的拉力转给钢筋，钢筋的应力突增，但没有达到屈服，使构件在破坏前形成多条裂缝。

当通过主裂缝处的纵筋和箍筋达到屈服强度后，第四个面上的受压区混凝土被压碎而破坏。

适筋破坏扭转角较大（图7-4曲线2），属于延性破坏，该类破坏模型是建立构件受扭承载力设计方法的试验依据。

（3）超筋破坏当抗扭钢筋数量过多，构件破坏时抗扭纵筋和箍筋均未达到屈服，破坏是由某相邻两条45°螺旋缝间混凝土被压碎引起的。

破坏形态见图7-3(c)，构件破坏时螺旋裂缝条数多而细，扭转角较小(图7-4曲线3)，属于超筋脆性破坏，构件承载力主要取决于截面尺寸及混凝土抗压强度。

这类破坏称为完全超筋破坏，在设计中应避免。

该类破坏模型是计算抗扭钢筋数量最大值的试验依据。

（4）部分超筋破坏当抗扭纵筋和抗扭箍筋数量比例不当，致使混凝土压碎时，箍筋或纵筋两者之一不能达到屈服点，这种破坏属于部分超筋破坏。

虽然结构在破坏时有一定延性，设计可用，但不经济。

2.什么是配筋强度比ζ的物理意义、计算公式与合理的取值范围。

答：配筋强度比ζ的物理意义：ζ为受扭构件纵向钢筋与箍筋的配筋强度比，如图7-5，其物理意义是协调抗扭纵筋和箍筋应合理配置，充分利用抗扭钢筋的作用，使受扭构件的破坏形态呈现适筋破坏。