当前位置：文档之家 › 电路原理(上)_ 相量法_

电路原理(上)_ 相量法_

  • 格式：pptx
  • 大小：1.23 MB
  • 文档页数：45

下载文档原格式

  / 45

合集下载

【第8章】 相量法

【第8章】 相量法
实轴 +1
复数在复平面上可 以用向量表示。
0
a1
2. 复数的四种表示形式
⑴ 表达式 ① 代数形式 A= a1+ ja2 +j a2 A
② 极坐标形式
③ 三角函数式 ④ 指数形式
0 模 幅角 A a cos j + j a sin j
A aj
a φ
a1 +1
A ae jj
（由欧拉公式e jφ = cos φ + jsin φ得到） ⑵ 四种表达式关系
I e jy i I y I m m m i
复振幅与正弦量的一一对应关系： 复振幅的模是正弦量的最大值 复振幅的幅角为正弦量的初相位
jy i I Ie Iy i 复有效值
复有效值与正弦量的一一对应关系： 复有效值的模是正弦量的有效值 复有效值的幅角为正弦量的初相位
同样可以建立正弦电压与相量的对应关系：
φ =0，同相； i i1
0 i2
φ = (180o) ，反相； i i1 i2
wt
0 i i1
wt
φ = /2，正交；
i2
wt 因为规定了： |φ| (180°)。 0 所以，我们说i1 领先 i2 /2, 而不说i2落后i1 3 /2
注：我们此处比较的是两个电流的相位差，那么，我们是 否可以比较一个电压和一个电流的相位差？在今后的分析 中可以利用电压和电流的相位差来判断电路的性质。
线圈从中性面开始转过了ωt 时，导线切割磁 力线的速度是ωr SIN ωt
可见：交流电是电流的大小和方向都随时间做周期 性变化的电流。
交流电有许多优点: •交流电可以用变压器升高或降低电压， •交流电可以驱动结构简单，运行可靠的交流 感应电动机，交流电是廉价的动力或能量来源。

电路相量法讲义

电路相量法讲义

1. 正弦量与相量之间的联系和区别；
2. 元件电压相量和电流相量的关系、相量图。
. Im= 5∠45o A
45o
. Um= 100∠0o V
主要是相位关系 .
Z = U.m =20∠-45o W Im
与其它章节的联系 是学习第 9、10、11、12章的基础。 必须熟练掌握相量法的解析运算。
2024年7月17日星期三
qA
任意一个复数A=|A|ejqa乘以
ejq ，等于把A逆时针旋转q
qa
+1
角度，而模|A|保持不变。 o
ej
p
2
=j
-j p
e 2 = -j
e jp = -1
都是旋 转因子
A×j = jA，等于把 A 逆时针旋转90o。
A j
=
-jA，等于把
A
顺时针旋转90o。
2024年7月17日星期三
7
§8-2 正弦量
di dt
=wImcos(wt+fi
(2) i1(t) =10cos(100pt+30o)A
i2(t) =10cos(100pt-105o)A (2) j =30o-(-105o)=135o
(3) u1(t) =10cos(100pt+30o)V (3) w1≠w2，
u2(t) =10cos(200pt+45o)V 不能进行相位比较。
fi = 60o
由于最大值发生在计
o t1
t
时起点右侧 fi = - 60o
i(t) = 100cos(103t - 60o)
2. 当 103t = 60o = p3 时， 出现最大值
t1 =

电路原理-相量法

电路原理-相量法
周期电流、电压有效值(effective value)定义
物 理 意 义
直流I
Rห้องสมุดไป่ตู้
交流i
R
W RI T
2
W Ri (t )dt
2 0
T
电流有效 值定义为
1 T 2 I i (t )dt T 0
def
有效值也称均方根值 (root-mean-square)
1 同样，可定义电压有效值： U T
8.1 复数
1. 复数的表示形式
Im b 向量 0 a Re 0 F
F=a+jb
( j 1 为虚单位）
Im b F |F|

①代数形式 ②三角形式
F a jb F | F | (cos j sin )
F | F | e j
F | F |
a
Re
③指数形式
④极坐标形式
除法：模相除，角相减
(3.41 j3.657) (9.063 j 4.226)
12.47 j 0.569 12.48 2.61
③ 旋转因子
Im
复数 ejθ =cosθ +jsinθ =1∠θ
F• e j 相当于F逆时针旋转一个角度θ ， ejθ 称为旋转因子。
j >0， u超前i，或i 落后u ，u 比i先到达最大值。 u, i u i
u i
j
O
t
j <0， i 超前 u，或u 滞后 i ，i 比 u 先到达最大值。
特殊相位关系：
①j ＝ 0， 同相 u, i u i ②j = (180 ) ，反相 u, i u 0 u, i u i 0 i t

电路原理 第八章_相量法

电路原理 第八章_相量法

复数 复数
—
孙惠英 shy@
上页
下页
返回
第8章
4、正弦量的相量表示法(续）
—
已知正弦量 220√ 2 cos ( ω t－35° ) 有效值相量 最大值相量 220/ －35° — 220√ 2 /－35°
已知 相量 10/45° and 正弦量的角频率ω 相应的正弦量 — 10 √ 2 cos( ωt + 45° )
0 ωt1
ωt2
ωt
φ
图8-5 用旋转矢量表示的正弦量
孙惠英 shy@
上页
下页
返回
第8章
4、正弦量的相量表示法 F = ⎪F⎪e j(ω t + ϕ )
ejθ = cosθ + jsinθ
设：有一复数
欧拉公式
F = ⎪F⎪ej(ωt + ϕ ) = ⎪F⎪cos(ωt + ϕ) + j⎪F⎪sin(ωt +ϕ) Re [F] = ⎪F⎪cos(ωt + ϕ ) Im [F] = ⎪F⎪sin(ωt + ϕ )
返回
第8章
三、旋转因子
/ϕ 旋转因子: e jϕ = 1 — A = ⎪A⎪ejα Aejϕ = ⎪A⎪ejαejϕ = ⎪A⎪ej(α+ϕ ) ejπ/2 = j1 e－jπ/2 = − j1
+j
Aejϕ
ϕ α
0
A
+1
e－jπ = − 1
孙惠英 shy@
上页
下页
返回
第8章
ϕ 12 = ϕ 1－ ϕ 2 —— u1 超前于 u2 的相角 ϕ 21 = ϕ 2－ ϕ 1 —— u2 超前于 u1 的相角

相量法

相量法

ω = 0(直流), X L = 0, 短路 ; ; ω → ∞, X L → ∞, 开路
ω
相量表达式: 相量表达式
& & & U = jX L I = jωLI ,
& = jB U = j − 1 U = 1 U & & & I L jωL ωL
返 回 上 页 下 页
波形图及相量图： 波形图及相量图：
返 回 上 页 下 页
电感元件VCR的相量形式 2. 电感元件 的相量形式
时域形式： 时域形式：
已知 i(t ) = 2I cos(ω t +ψi )
i(t) + uL(t) •
则
L
di(t ) uL (t ) = L = − 2ωL I sin(ω t +Ψ ) i dt π = 2ω L I cos(ω t +Ψ + ) i 2
uL O
pL i
2π π
& UL
电压超前电 流900
& I
ωt
Ψi
功率： 功率：
pL = uLi = ULm Im cos(ωt +Ψ ) sin(ω t +Ψ ) i i = UL I sin 2(ω t +Ψ ) i
瞬时功率以2ω交变，有正有负，一周期内刚好互相抵消 瞬时功率以 ω交变，有正有负，
返 回 上 页 下 页
波形图及相量图： 波形图及相量图： pR uR i
& UR
URI
& I
Ψu=Ψi
同 相 位
O
ωt
瞬时功率： 瞬时功率：
pR = uRi = 2UR 2I cos2 (ω t +Ψ i )

电路(第五版).-邱关源原著-电路教案--第8章相量法

电路(第五版).-邱关源原著-电路教案--第8章相量法

电路(第五版).-邱关源原著-电路教案--第8章相量法第8章 相量法● 本章重点1、正弦量的两种表示形式；2、相量的概念；3、KVL 、KCL 及元件VCR 的相量形式。

● 本章难点1、 正确理解正弦量的两种表示形式的对应关系；2、 三种元件伏安关系的相量形式的正确理解。

● 教学方法本章是相量法的基础，对复数和正弦量两部分内容主要以自学为主，本章主要讲授相量法的概念、电路定律的相量形式以及元件V AR 的相量形式。

讲述中对重点内容不仅要讲把基本概念讲解透彻，而且要讲明正弦量的相量与正弦时间函数之间的对应关系；元件V AR 的相量形式与时域形式之间的对应关系，使学生加深对内容的理解并牢固掌握。

本章对元件的功率和能量这部分内容作了简单讲解，以便为下一章的学习打下基础。

本章共用4课时。

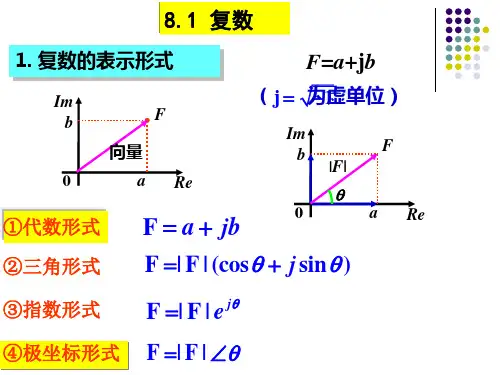
● 授课内容8.1复数1. 复数的三种表示bj a A += 直角坐标=θ∠r 极坐标 =θj re 指数形式θθθsin cos 22r b r a ab arctgb a r ==⇒=+=⇒直极极直θθsin cos jr r A += 三角表示形式欧拉公式：θθθsin cos j e j +=2. 复数的运算已知：11111θ∠=+=r jb a A ，22222θ∠=+=r jb a A求：212121,,A AA A A A ⋅±i()()212121b b j a a A A ±+±=±212121212121θθθθ+∠=+∠=⋅r r A A r r A A 8.2正弦量一、正弦量：随时间t 按照正弦规律变化的物理量，都称为正弦量，它们在某时刻的值称为该时刻的瞬时值，则正弦电压和电流分别用小写字母i 、u 表示。

周期量：时变电压和电流的波形周期性的重复出现。

周期T ：每一个瞬时值重复出现的最小时间间隔，单位：秒（S ）； 频率f ： 是每秒中周期量变化的周期数，单位：赫兹（Hz ）。

电路原理课件 第8章 相量法

电路原理课件 第8章 相量法

三. 相位差 ：
两个同频率正弦量相位角之差。
i(t) 0
Im um
设 u(t)=Umcos(w t+ u)
2
i(t)=Imcos(w t+ i)
0
wt
则 相位差j : j = (w t+ u)- (w t+ i)
u- i
同频率正弦量的相位差等于它们的初相之差。 不同频率的两个正弦量之间的相位差不再是一个常数，而是 随时间变动。
j u与i正交; j u与i反相;
2
§8 - 3相量法的基础
1. 正弦量的相量表示
复函数 F F ej(wt)
没有物理意义
F cos(wt ) j F sin(wt Ψ )
若对F取实部：
Re[F] F cos(ωt Ψ ) 是一个正弦量，有物理意义。
对于任意一个正弦时间函数都可以找到唯一的与其对应的 复指数函数：
F e j
4、极坐标形式：
F F ej
=|F|
二 复数运算
(1)加减运算——代数形式
+j F2
若 F1=a1+jb1
F2=a2+jb2 O
则 F1±F2= (a1±a2) +j (b1±b2)
F= F1 +F1
F1 +1
+j
O - F2
F2 F1
F= F1 - F2 +1
(2) 乘除运算——指数形式或极坐标形式
⑶∫i2dt。
解： ⑴设 i i1 i2 2I cos(wt i ), 其相量为 I=I/Ψi
I I1 I2 10/600A+22/-1500A=（5+j8.66）A+（-19.05-j11）A

电路_相量法

电路_相量法

8
相量法的基础(****) §8 - 3 相量法的基础
§8 - 3 相量法的基础
一、相量定义： 相量定义：
表示正弦量的复常数称为相量。 表示正弦量的复常数称为相量。 例如： 例如： 正弦量 i = 220 2 cos(314t − 30 o )A
& = 220 e − j30o A 表示。 表示。 可用相量 I
& = Re[ 2 I e e jω t ] = Re[ 2 I e jω t ]
三、正弦量的运算： 正弦量的运算：
1、同频正弦量的代数和： 、同频正弦量的代数和： i1 = 2 I1 cos(ω t + ψ 1 )A， i2 = 2 I 2 cos(ω t + ψ 2 )A
& & & & i = i1 + i2 = Re[ 2 I1 e jω t ] + Re[ 2 I 2 e jω t ] = Re[ 2 ( I1 + I 2 )e jω t ]
2π ω = 2πf = T
额定值为有效值， 额定值为有效值， 耐压值为最大值。 耐压值为最大值。
热效应上与一个周期内的平均效应相等的直流值。 热效应上与一个周期内的平均效应相等的直流值。 ③有效值： 有效值： 周期电流的有效值： 周期电流的有效值： = I 正弦电流的有效值： 正弦电流的有效值：I =
& I =Ie
jψ i
& = ωI e jψ i +90o = ωI e jψ i ⋅e90o = jωI e jψ i = jωI & ∴Y
结论： 正弦量的微分为同频正弦量，对应的相量为原相量乘以 jω。 结论： 正弦量的微分为同频正弦量， 。 注意：不能说“ 的函数。 注意：不能说“相量的导数为相量乘 jω” 。 因为相量不是 t 的函数。 11

电路分析基础课件第6章 相量法

电路分析基础课件第6章 相量法

+j
设相量
相量 乘以 ，
将逆时针旋转 90， 得到
A
0ψ +1
相量 乘以
，
- A
将顺时针旋转 90，得到
应用举例
例： 6-5 在图示相量图中， 己知I1=10A， I2=5A, U=110V， f=50Hz，试分别写出 它们的 相量表达式和瞬时值表达式，并说明它们之间的相位关系。
解： 相量表达式为 I1 10 30 A I2 5 45 A
F2
(1) 加法运算：
F1 F2 (a1 a2 ) j(b1 b2 )
F1 +1
F1 F2 F2
(2) 减法运算：
作图方法：首尾相连
F1 F2 (a1 a2 ) j(b1 b2 )
平行四边形
(3) 乘法运算：
F1 F2 F1 F2 (1 2 )
试分别画出它们的波形图，求出它们的有效值、频率及相位差。
解：u 10 2sin(314t 30)
i、u
10 2cos(314t 120)
ui
i、u波形图如图所示。其有效值为
I 20 14.142Α 2
0 π 2π ωt
U 10V
i、u 的频率为 f ω 314 50Hz
2π 2 3.14
u、i 的相位差为：
ψu ψi 120 60 180
应用举例
例： 6-3已知正弦电压 u 311cos(314t 60)V，试求：(1)角频率ω、频率f、周期T、
最大值Um和初相位Ψu ；(2)在t=0和t=0.001s时，电压的瞬时值；(3)用交流电压 表去测量电压时，电压表的读数应为多少？

【电路理论电子教案】相量法

【电路理论电子教案】相量法

CH8 相量法本章介绍相量法。

主要内容有：复数，正弦量，相量法的基础，电路定律的相量形式。

§8-1 复数教学目的：复习复数的基本知识，为学习相量法做基础。

教学重点：复数；旋转因子。

教学难点：旋转因子。

教学方法：自学。

教学内容：一、复数的表示形式1．代数形式：F=a+jb 模：F =22b a + 复角：=θarctan ab 2．三角形式：F=F （cos θ+sin θ） 模：F 复角：θ 3．指数形式：F=F eθj 模：F 复角：θ4．极坐标形式：F=F ∠θ模：F 复角：θ二、复数的运算 教材P 175~1741．复数的加减 2．复数的乘除3．复数的有理化运算三、旋转因子 e θj 教材P 175§8-2 正旋量教学目的：复习正弦量的三要素，学习正弦量的有效值，以及同频正弦量的相位差。

教学重点：正弦量的三要素，同频正弦量的相位差。

教学难点：相位差的计算。

教学方法：课堂讲授。

教学内容：一、正旋量的三要素1．定义：教材P 1762．三要素：教材P 177~176 i ψ≤180ο3．ω、T 、f ： 教材P 177二、正旋量的有效值1．有效值定义：根据焦耳-愣次定律，当周期电流信号i(t)流过R 时，一个T 内电阻所消耗的能量为：1ω=⎰T dt t p 0)(=⎰Tdt t Ri 02)(；直流电流I 流过电阻R 时,在相同时间T 内，该电阻消耗的能量为：2ω=⎰Tdt RI 02=RI 2T 。

如果上述两种情况中，电阻R 消耗的能量相同，即 1ω=2ω 则有RI 2T=⎰Tdt t Ri 02)( 即：I=⎰T dt t i T 02)(1。

2．有效值与最大值的关系：I m =2I三、同频正旋量的相位差1．相位差：同频正旋量的相位差等于它们的初相之差，与记时零点的选取、变化无关。

2．取值：12ψ≤π（设12ψ与U 1与U 2的相位差） （1）12ψ>0 U 1超前U 212ψ（U 2滞后U 112ψ） （2）12ψ<0 U 1滞后U 212ψ（U 2超前U 112ψ） （3）12ψ=0 U 1、U 2同相 （4）12ψ=π± U 1、U 2反相 （5）12ψ=±2πU 1、U 2正交 [例1]：已知u 1=2202cos(ωt-120°)，u 2=2202cos(ωt+120°) ，求相位差。

第三章 相量法

第三章 相量法

= I m cos(ωt + ψ i ) 则代入上式求得: I =
Em Um ,E = 2 2
（只适合于正弦波）
Im 2
同理:
U=
表达式又可以写成：
i (t ) =
2 I cos( ω t + ψ i ) （A）, u ( t ) =
2 U cos( ω t + ψ u ) （V）
《电路原理》 教案
=
∫ Re[
I& m ⋅ e
] ⋅ dt = Re[
∫ I&
m
⋅ e j ω t ⋅dt ]
e jω t & = Re[ I m ⋅ ] jω
& I & Fm = m jω
3. 微分运算： 设： i (t )
& = I ∠ψ = I m cos(ωt + ψ i ) ⎯表示为 ⎯⎯→ I m m i
《电路原理》 教案
第三章 相量法
任课教师：贾玉福
共 10 页
第7页
则：
∑U &
k =1 P
km
=0
或
& ∑U
k =1
P
k
=0
其它定理、方法均由 KCL、KVL 得来,故均可用相量形式表示. 二.R、L、C 元件 VAR 的相量形式 1. 纯电阻：
u R = R ⋅ iR
设： iR
表示为 & = I ∠ψ = 2 I R cos(ωt + ψ i ) ⎯⎯ ⎯→ I R R i
直流产生的热量:
交流产生的热量：
WD = I 2 RT （J）
当 WD = W A 时则： I =
W A = ∫ i 2 Rdt （J）

电路知识：正弦交流电路与其分析方法“相量法”(上)

电路知识：正弦交流电路与其分析方法“相量法”(上)

电路知识：正弦交流电路与其分析方法“相量法”（上）“相量是什么？它和向量、矢量有什么区别？”，相信不少电工朋友都有着这样的疑问。

正如标题所示，相量是用于正弦交流电路分析的，换言之，离开正弦交流电路，相量将毫无意义。

而它与向量、矢量的区别，在看完本文后，你将能给出自己的答案。

掌握相量法，我们就可以快速并简单地对正弦交流电路进行分析、计算并理解其各种特性，包括电压电流、阻抗、有功功率以及无功功率等。

基于相量法的便捷性，本文将给大家详细讲解相量的含义以及运算，让大家学以致用，在交流电路分析中得心应手。

相量用于表示正弦交流电路中的各种正弦量，如电压、电流、磁通等。

所谓正弦量，是指电路中按正弦规律变化的各种物理量。

所以在理解相量前，我们有必要指定什么是正弦交流电路以及正弦量。

NO. 1正弦交流电路与正弦量电路有交流和直流之分，如下图1-1所示为不同形式的交流量和直流量波形图。

图1-1图（1）所示为恒定直流量的波形，例如电池的电压，在一定情况下就保持为恒定值。

而图（2）就是本文的主角，正弦交流量，即正弦量。

比较图1-1中的几种波形，可以发现，所谓直流量，不仅仅是指恒定直流量，还包括大小变化的各种时变量，如图（3）、图（6）的锯齿波，它们大小随时间变化，但方向保持不变，所以它们是直流量。

而交流，区别于直流，是指电路中的电压、电流等物理量方向发生变化，但大小不一定变化，例如图（4）的矩形波，该电流方向作周期变化，但其大小保持不变。

含有正弦电源且电路中各部分产生的电压、电流均按正弦规律变化的电路，就是正弦交流电路。

所谓正弦规律变化，正如图1-1中的图（2）所示。

在这里要说明一点，“正弦规律”不一定指正弦函数，其实余弦函数也是按正弦规律变化的，因为余弦函数可以由正弦函数左移90°得到。

所以上文提到的“正弦规律”指的是一种变化规律，而不是指正弦函数。

例如图1-2所示的电流和电压，都属于正弦量。

但在同一个电路中，一旦确定所用的函数，那么所有正弦量都应该用同一种函数表示，例如确定用sine正弦函数，就不能出现consine余弦函数，即使有，也应该根据三角函数换算转化为sine函数表示，这也是为了便于它们进行相位的比较。

《电路原理相量法》课件

《电路原理相量法》课件

05 相量法的实验验证
CHAPTER
实验设备与器材
电源
提供稳定的交流电，模拟真实 电路中的电源。
电阻、电容和电感
用于构建各种电路，验证相量 法的理论。
示波器
用于观察和记录实验中的电压 和电流波形。
数据采集器和计算机
用于实时采集和处理实验数据 。
实验步骤与操作
3. 开启电源
2. 设置测量参数
设定示波器的采样率、电压范围 等参数，确保能够准确记录波形 。
音频处理
相量法用于分析声音信号的频率和相位，以进行 音频处理和编辑。
谢谢
THANKS
电阻元件的相量模型
总结词
描述电阻元件在相量法中的数学 模型和特性。
详细描述
电阻元件的相量模型是一个实数 ，表示其纯实部的阻抗。在相量 图中，电阻元件的相量位于实轴 上。
04 相量法的电路分析
CHAPTER
简单电路的相量分析
总结词：简单明了
详细描述：对于简单的电阻、电容、电感电路，可以使用相量法进行直观分析， 通过相量图和公式计算得出结果。
《电路原理相量法》ppt课件
目录
CONTENTS
• 相量法简介 • 相量法的数学基础 • 电路元件的相量模型 • 相量法的电路分析 • 相量法的实验验证 • 相量法在日常生活中的应用
01 相量法简介
CHAPTER
相量法的定义
相量法是一种分析正弦稳态电路的方 法，通过引入相量来描述正弦量，将 时域中的正弦稳态电路转换为复平面 上的向量图，从而简化计算过程。
CHAPTER
复数及其运算
复数的定义
由实部和虚部组成的数，表示为 a + bi，其中 a 是实部，b 是虚部，i 是 虚数单位。

相量法

相量法
b I1 Sin1 I 2 Sin2
I a b
2 2
I

jb a
29
b arctg a
3. 两相量积的代数表示 设 ju
U Ue
*
Ie ji I
I Ie * ~ j u j i S U I Ue Ie
j i
UIe
6
例如：
f 50Hz 50kHz 50MHz T 20ms 20us 0.02us 6000km 6km 6m
工频 低频 甚高频
7
第1节、复数
• F=a+bi • 复数的相量表示 • 复数的基本运算
8
第2节、正弦量（正弦交流信号）
• F(t) = F0Cos(t+) • i(t) = ImCos(t+i) • u(t) = UmCos(t+u)
U bc 8 30V 2
相量 时域 相量图
47
uac 5.03Cos(t 67.4)V
5.03 67.4V U ac 2
相量法求解正弦稳态解的过程回顾
时域模型 相量模型
时域方程 相量方程
解微分方程
时域解
相量解
48
(t)


t
A(t )

t=0
21
旋转矢量

A(t )
模
旋转角速
A

振幅 ACos(t ) A
正弦量
角频率
初相

t = 0时与实轴夹角

22
设
i1 2 I1Cos(t 1 )
i 2 2I 2Cos(t 2 )
i1 i 2 Re[ A1 (t )] Re[ A2 (t )] Re[ A1 (t ) A2 (t )]

chapter08相量法电路原理

chapter08相量法电路原理

N
线性
w1
w2
N
线性
w非
线性
不适用 ③ 相量法可以用来求强制分量是正弦量的任意常系数线
性微分方程的特解，即可用来分析正弦稳态电路。
8.3 电阻、电感和电容元件上电压 和电流的相量关系
一. 电阻
i(t)
+ uR(t) -
已i知 (t)2Isiw n ty ()
wy 则 u R (t) R (t) i2 R sI itn )(
L
iR
jw L
+ iL
iC
uS
C
-
+ IL
R
US
-
IR
IC
1/jw C R
时域电路
iL iC iR
LdiL1
dt C
iCdt uS
1
RiR C iCdt
时域列写微分方程
相量模型
IL I C IR
jwLILjw1CI C US
RIR
1
jwC
IC
相量形式代数方程
相量模型：电压、电流用相量；元件用复数阻抗或导纳。
画相量图：选电流为参考向量(w L > 1/w C )
ULUUCj来自URIU
j
UX
UR
电压三角形
U UR 2 UX 2
.
IR
+
.
+ UR-
请看演示
三. 相量图
ωy y i(t)2 I sitn i() I I i
wy y u (t)2 U sitn u ( ) U U u
•
U
•
I
yu yi
四. 相量运算
(1) 同频率正弦量相加减

电路第8章相量法

电路第8章相量法
注意
相量的模表示正弦量的有效值
相量的幅角表示正弦量的初相位
返 回 上 页 下 页
同样可以建立正弦电压与相量的对应关系：
u(t ) 2U cos( t θ ) U Uθ

例1
i 141.4 cos(314t 30o )A 已知 o u 311.1cos(314t 60 )V
jX L j4 5 j20
1 jX C j j10Ω 5 0.02
返 回 上 页 下 页
U U U I IR IL IC R j X L jX C
微分运算 积分运算
di d e j t Re 2 I j e j t Re 2 I dt dt I j t j t idt Re 2 Ie dt Re 2 e j






di dt
j I I i π
I2
4. Z 2 jX C , I 0 I1 8A, I 2 16A
返 回
例3 已知 u(t ) 120 2 cos(5t ), 求 : i(t )
i +
15
4H
0.02F 相量模型
_ u
U _
I 15 -j10 +
j20
I1
I2
I3
解
12000 U
返 回 上 页 下 页
4、线性受控源
ik 0
Ik 0

uk
ij
uj


Uk

Uj
Ij
VCCS（电压控制的电流源）
相量模型
i j guk

电路原理习题答案相量法

电路原理习题答案相量法

第八章相量法求解电路的正弦稳态响应，在数学上是求非齐次微分方程的特解。

引用相量法使求解微分方程特解的运算变为复数的代数运运算，从儿大大简化了正弦稳态响应的数学运算。

所谓相量法，就是电压、电流用相量表示，RLC元件用阻抗或导纳表示，画出电路的相量模型，利用KCL,KVL和欧姆定律的相量形式列写出未知电压、电流相量的代数方程加以求解，因此，应用相量法应熟练掌握：（1）正弦信号的相量表示；（2）KCL,KVL的相量表示；（3）RLC元件伏安关系式的相量形式；（4）复数的运算。

这就是用相量分析电路的理论根据。

8－1将下列复数化为极坐标形式：（1）；（2）；（3）；（4）；（5）；（6）。

解：（1）(因在第三象限)故的极坐标形式为（2）（在第二象限）（3）（4）（5）（6）注：一个复数可以用代数型表示，也可以用极坐标型或指数型表示，即,它们相互转换的关系为：和需要指出的，在转换过程中要注意F在复平面上所在的象限，它关系到的取值及实部和虚部的正负。

8－2将下列复数化为代数形式：（1）；（2）；（3）；（4）；（5）；（6）。

解：（1）（2）（3）（4）（5）（6）8－3若。

求和。

解：原式=根据复数相等的定义，应有实部和实部相等，即虚部和虚部相等把以上两式相加，得等式解得所以8－4求8－1题中的和。

解：8－5 求8－2题中的和。

解：8－6若已知。

（1）写出上述电流的相量，并绘出它们的相量图；（2）与和与的相位差；（3）绘出的波形图；（4）若将表达式中的负号去掉将意味着什么（5）求的周期T和频率f。

解：（1）故，和的相量表达式为其相量图如题解图（a）所示。

题解8－6图（2）（3）（t）的波形图见题解图（b）所示。

（4）若将（t）中的负号去掉，意味着的初相位超前了180。

即的参考方向反向。

（5）（t）的周期和频率分别为注：定义两个同频率的正弦信号的相位差等于它们的初相之差，因此在比较相位差时，两个正弦量必须满足（1）同频率；（2）同函数，即都是正弦或都是余弦；（3）同符合，即都为正号或都为负号，才能进行比较。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2U 2
e
j t
)
Re(
2U1
e
j t
2U
2
e
j
t
)
Re[
2(U1U 2) e
j t ]
相量关系为：
U
U U1 U2
结论： 同频正弦量的加减运算变为对应相量的加减运算。
8
相量法的基础
电路 原理
i1 i2= i3
I1 I2 I3
例3 u1(t) 6 2cos(314t 30 ) V
u2(t) 4 2cos(314t 60 o) V
u 311.1cos(314t 67) V
试用相量表示i, u。
解
I 100 50A, U 220 67V
例2 已知I 60 30 A , f 50Hz , 试写出电流的瞬时值表达式。
解
i 60 2cos(314t 30) A
6
相量法的基础
相量图
在复平面上用矢量表示相量的图。
u(t) 2Ucos( t θ) U U
j t
Re 2Ie dt Re 2
I j t e
j
dij
dt
IIi
+π
2
II idt j
i 2
11
相量法的基础
电路 原理
例4 用相量运算：
i(t)
+R
u(t)
L
-
C
i(t) 2I cos( t i)
u(t) Ri L di 1 idt dt C
| F |
a2 b2
b
或
θ
arctan( ) a
二. 复数运算
Im
b
F
|F|
O
a
Re
a | F | cos
b |F|sin
① 加减运算 —— 采用代数式
3
复数
若 F1=a1+jb1， F2=a2+jb2，则 F1± F2=(a1± a2)+j(b1± b2).
电路 原理
Im F2
F1+F2
Im
正弦量对应的 相量
i(t) 2I cos( t ) I I
注意： ① 相量的模表示正弦量的有效值。 ② 相量的幅角表示正弦量的初相位。
5
相量法的基础
电路 原理
同样可以建立正弦电压与相量的对应关系
u(t) 2U cos( t ) U U
例1 已知 i 141.4cos(314t 50) A
) j
2
2
2
F
F
Re
Im
F
O
Re
jF
7
复数
电路 原理
π
π j
ππ
jF
, e 2 cos( ) jsin( ) j
2
2
2
Im
F
j , e cos( ) jsin( )
1
O
F
Re jF
+j, –j, -1 都可以看成旋转因子
8
相量法的基础
1
相量法的基础
电路 原理
一. 问题的提出 电路方程是微分方程
tI 3
3
结论： 同频的正弦量相加仍得到同频的正弦量，所以，只需确定初相位和
有效值。因此采用
正弦量
复数
变换的思想
3
相量法的基础
电路 原理
二. 正弦量的相量表示
无物理意义
造一个复数函数 F(t) 2Ie j( t)
2Icos(t ) j 2Isin(t )
对 F(t) 取实部 Re[F(t)] 2Icos( t ) i(t)
结论：
是一个正弦量 有物 理意义
任意一个正弦时间函数都有唯一与其对应的复数函数。
j( t )
i 2Icos( t ) F(t) 2Ie
4
相量法的基础电路 原理Ft) 还可以写成复常数
F(t)
2Ie j e jt 2Ie jt
F(t) 包含了三要素：I、 、 复常数包含了两个要素：I 、
LC d2 uC RC duC uC u(t)
dt
dt
+R u
-
iL L
+
uC -C
两个正弦量的相加，如KCL、KVL方程运算：
i1 2I1 cos( t 1) i2 2I2 cos( t 2)
2
相量法的基础
电路 原理
u i1, i
i2
i1
角频率
i2
有效值 I1 O
I2
初相位 1
2
i1+i2i3 i3
+j
U
O 三. 相量法的应用
I
+1
① 同频率正弦量的加减
电路 原理
7
相量法的基础
电路 原理
u1(t)
2U1 cos( t 1) Re( 2U1 e
j t )
u2(t) 2U2 cos( t 2) Re( 2U 2 ej t )
u(t) u1(t) u2(t) Re( 2U1 e
j t ) Re(
10 j6.2820 j31.9
11.8132.1337.6557.61 39.4540.5
10.89 j2.86
=(3 34)(34)j
=9.2+7j ③ 旋转因子
复数
ej=cos +jsin =1∠
6
复数
电路 原理
Im F• ej
F• ej
旋转因子
O
jF
特殊旋转因子
π,
π j
e2
ππ cos( ) jsin(
复数
1
一. 复数的表示形式
F a jb
j 1 为虚数单位
F | F | e j
复数
电路 原理
Im
代数式
b
F
|F|
O 指数式
a
Re
三角函数式
F | F | (cos jsin )
F | F |
极坐标式
2
复数
电路 原理
几种表示法的转换关系：
F a jb
F | F | e j | F |
| F e |1 j(θ1 2 θ ) |F 2|
| F 1| θ1θ2 |F2 |
模相除 角相减
5
复数
电路 原理
例: 计算
1. 630 + 4 + 4j =6cos306j(sin30) 4 4j
=6 3 61 j44j
2
2
=3 3+3j44j
(10 j6.28)(20 j31.9)
2.
U1 630 V U2 460 V
U U1 U2 630 460
5.19 j3 2 j3.46 7.19 j6.46
9.6441.9 V
u(t) u1(t) u2(t) 9.64 2cos(314t 41.9 ) V
9
相量法的基础
电路 原理
借助相量图计算
U1 6 30 o V
F1+F2 F2
O 图解法
F1
Re
O
F1-F2
F1 Re
-F2
4
复数
②乘除运算 —— 采用极坐标式
若 F1=|F1|∠ 1 ，F2=|F2|∠ 2
则
F 1F2 F 1 ej1 F2 ej2 F 1 F e2 j(12)
F 1 F2 1 2
电路 原理
模相乘 角相加
F 1 | F |e1 jθ1 F2 | F |2e jθ2
U 2 4 60o V
+j
+j
U
U2
U1
60
30 41.9
O
+1
O
U
U2
U1
60
30 41.9
+1
首尾相接
10
相量法的基础
电路 原理
② 正弦量的微分、积分运算
i 2I cos( t i) I Ii
微分运算 积分运算
di dt
d dt
Re
2Ie j t
Re 2I j ej t
idt