《数理统计》第7章(0-1)分布参数的
- 格式:ppt
- 大小:471.50 KB
- 文档页数:7




习题7-11.选择题(1)设总体X 的均值口与方差 /都存在但未知,而X 1,X 2,L ,X n 为来自X 的样本,则均值 口与方差 (T 2的矩估计量分别是 ().(A) X 和(B)1 nX 和—(Xn i 1i )2.(C)口和 2(T・1 (D) X 和一 nn(X ii 1 x)2.解 选(D).(2) 设X : U[0,],其中 e >0为未知参数,又X ,,X 2,L ,X n 为来自总体X 的样本 ,则e 的矩估计量是().(A) X . (B)2X . (C)max{X i }.(D)mi^X i}.解选(B).2.设总体X 其中0v B v 为未知参数,X1, X 2,…,X.为来自总体X 的样本,试求e 的矩 估计量.解 因为 E (X )=(- 2)x3 e +1x (1 -4 e )+5x e =1-5 e ,令 1 5 X 得到的矩估计量为3.设总体X 的概率密度为f(x ;)(1)x ,0 x 1,0,其它•其中 0> -1是未知参数,X ,冷… ,X n 是来自 X 的容量为n 的简单随机样本求:(1) 的矩估计量;⑵ 0的极大似然估计量•解 总体X 的数学期望为-19 2X 1令E(X) X ,即一1 X,得参数B 的矩估计量为?•21 X设X 1, X 2,…,x n 是相应于样本X 1, X 2,…,X n 的一组观测值,则似然函 数为n(1)n X i , 0x i 1,i 10,其它.In xi 1In X ii 14.设总体X 服从参数为的指数分布,即X 的概率密度为E(X)1xf(x)dx o (1)x dx当 0<X i <1(i =1,2,3,…,n )时,L >0 且 In L nln(1)In X i ,i 1dln LnIn x =0,得0的极大似然估计值为而0的极大似然估计量为f(X,xe , x 0,其中0为未知参数,X, X2,)0, x< 0,…,X n为来自总体X的样本,试求未知参数的矩估计量与极大似然估计量解因为E(X)= 1= X , 所以的矩估计量为设X1, X2,…,x n是相应于样本X i, X2,…,X 的一组观测值,则似然函数取对数Xii 1然估计量为In L 0,得5.设总体X的概率密度为f (x,) 其中(0< <1)是未知参数.X, N为样本值x1, X2,L ,x n中小于极大似然估计量•解⑴ X E(X) xnInnXn e 11X).的极大似然估计值为1,的极大似X0,X2,0x1,, 1< x< 2,其它,…,X n为来自总体的简单随机样本,记1的个数.dx 2x(1求:(1)e的矩估计量;(2)e的3 3 —)dx ,所以矩一X .2 21⑵ 设样本X ,X 2 ,L X n 按照从小到大为序(即顺序统计量的观测值)有如下关系:X (1) w X (2)X ( Ni <1 W X ( N +1) W X (N+2)X (n ).似然函数为N n NL()(1 ),X (1) w X (2) w L w X ( N ) 1W X (N1) W X (N2) w L w X n ,0,其它.考虑似然函数非零部分,得到In L ( 0 ) = N ln 0 + ( n -N ) ln(1 - 0 ),令d |nL ( )」o ,解得0的极大似然估计值为? N .d1n习题7-2的无偏估计量•1.选择题:设总体X 的均值与方差 2都存在但未知,X i ,X 2,L ,X n 为X 的样本,则无论总体 X 服从什么分布,()1X i和丄 (XiX)2.(B)n i 1 n i1 n(C)X i 和n 1 i 1解 选(D).2.若X 1 ,X 2lx1 1X 2kX 334解 要求E( 7X 1-X j 和丄 1 i 1 n 1n(X ii 1X)2.(X i1)2 • (D)X i 和丄(X i)2.X 3为来 自总体X : N(,2)的样本,且的无偏估计量,问k 等于多少1 11 「2 kX 3)3 4k解之,k=g(A)13.设总体X的均值为0,方差2存在但未知,又X「X2为来自总体X1 2 2的样本,试证:—(X i X2)为的无偏估计21 2 1 2 2证因为E[—(X i X2) ] —E[(X i 2X^2 X2 )]2 2-[E(X i2) 2E(X i X2)E(X22)]-2 2所以-(X i X2)2为2的无偏估计•2习题7-31.选择题(1)总体未知参数的置信水平为的置信区间的意义是指()(A)区间平均含总体95%的值.(B)区间平均含样本95%的值.(C) 未知参数有95%的可靠程度落入此区间.(D) 区间有95%的可靠程度含参数的真值•解选(D).(2)对于置信水平1- a (0< a <1),关于置信区间的可靠程度与精确程度F列说法不正确的是().(A)若可靠程度越咼,则置信区间包含未知参数真值的可能性越大(B)如果a越小,则可靠程度越高,精确程度越低•(C)如杲1 - a越小,则可靠程度越高,精确程度越低•(D)若精确程度越高,则可靠程度越低,而1- a越小.解选(C)习题7-41. 某灯泡厂从当天生产的灯泡中随机抽取9只进行寿命测试,取得数据如下(单位:小时): 1050, 1100, 1080 , 1120, 1250, 1040, 1130, 1300, 1200设灯泡寿命服从正态分布 N 口 , 902),取置信度为,试求当天生产的全部灯泡的平均寿命的置信区间所求置信区间为(x - z /2 , X - z /2 ) \l n J n 90 90 (1141.11 = 1.96,1141.11 r 1.96)V 9V 9(1082.31,1199.91).2.为调查某地旅游者的平均消费水平,随机访问了40名旅游者,算得平均消费额为 X 105元,样本标准差s 28元•设消费额服从正态分布 取置信水平为,求该地旅游者的平均消费额的置信区间解计算可得X 105, s 2 =282.对于a =,查表可得t_(n 1) t o.025(39)2.0227.2所求口的置信区间为3. 假设某种香烟的尼古丁含量服从正态分布 .现随机抽取此种香烟 8支解计算得到X1141.11, CT 2 =902.对于a =,查表可得Z /2Z).Q25匸96*(Xt (n 1), x ■■- n 2s —t (n ■■- n 21)) (1052.0227, 1052.0227)2828为一组样本,测得其尼古丁平均含量为毫克,样本标准差s=毫克.试求此种香烟尼古丁含量的总体方差的置信水平为的置信区间.a =,查表可得 2(n 1) 爲5(7) 20.278,并说明该置信区间的实际意义1 2的置信水平为的置信区间是,”的实际意义是:在两总体第一个正态总体的均值1比第二个正态总体均值 2大〜,此结 论的可靠性达到95%.5.某商场为了了解居民对某种商品的需求 ,调查了 100户,得出每户月2解已知n =8, s2 2 (n 1)0.995(7) 1 - 20.989,所以方差d 2的置信区间为((n 1)S 2(2_ (n 1)22 22(8 1) 2.4 (8 1) 2.4 _2 —)(, )=,.2(n 廿丿 20.2780.9891 -(n 1)S 4.某厂利用两条自动化流水线灌装番茄酱 ,分别从两条流水线上抽取样本:X ,X 2,…,X 12 及 Y ,Y 2,…,丫17,算出 x 10.6g, y2 29.5g, s 1 2.4, s 2 4.7 .假设这两条流水线上装的番茄酱的重量都服从正态分布 ,且相互独立,其均值分别为2又设两总体方差1:.求2置信水平为的置信区间解由题设2 2x 10.6,y 9.5,s 12.4, s 2 4.7,n12,n 2 17,m 1)s 2 仏 1)s :(12 1) 2.4(171) 471.94212 17 2t_gn 22q n 2 22) t °.°25(27)2.05181,所求置信区间为((X y)11) ((10.6 9.5) 2.05181 1.94结论“方差相等时, [(a n 22)s w2)平均需求量为10公斤,方差为9 .如果这种商品供应10000户,取置信水平为•(1) 取置信度为,试对居民对此种商品的平均月需求量进行区间估计(2) 问最少要准备多少这种商品才能以99%的概率满足需要解(1) 每户居民的需求量的置信区间为_ s(xt(n* n_ s1), xt (nV n1)) (xs卅,%s川)(10,9J492.575,10 2.575)(9.2275,10.7725). 100J10010000户居民对此种商品月需求量的置信度为的置信区间为(92275,107725);(2)最少要准备92275公斤商品才能以99%的概率满足需要。


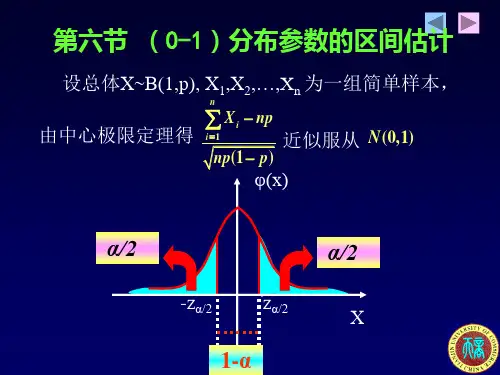




概率论与数理统计第7章参数估计习题及答案第7章参数估计 ----点估计⼀、填空题1、设总体X 服从⼆项分布),(p N B ,10<计量=pXN. 2、设总体)p ,1(B ~X,其中未知参数 01<则 p 的矩估计为_∑=n 1i i X n 1_,样本的似然函数为_ii X 1n1i X )p 1(p -=-∏__。
3、设 12,,,n X X X 是来⾃总体 ),(N ~X 2σµ的样本,则有关于 µ及σ2的似然函数212(,,;,)n L X X X µσ=_2i 2)X (21n1i e21µ-σ-=∏σπ__。
⼆、计算题1、设总体X 具有分布密度(;)(1),01f x x x ααα=+<<,其中1->α是未知参数,n X X X ,,21为⼀个样本,试求参数α的矩估计和极⼤似然估计.解:因?++=+=101α2α1α102++=++=+|a x 令2α1α++==??)(X X EXX --=∴112α为α的矩估计因似然函数1212(,,;)(1)()n n n L x x x x x x ααα=+∑=++=∴ni i X n L 1α1αln )ln(ln ,由∑==++=??ni i X nL 101ααln ln 得,α的极⼤似量估计量为)ln (?∑=+-=ni iXn11α2、设总体X 服从指数分布 ,0()0,x e x f x λλ-?>=??其他,n X X X ,,21是来⾃X 的样本,(1)求未知参数λ的矩估计;(2)求λ的极⼤似然估计.解:(1)由于1()E X λ=,令11X Xλλ=?=i x nn L x x x eλλ=-∑=111ln ln ln 0nii ni ni ii L n x d L n n x d xλλλλλ====-=-=?=∑∑∑故λ的极⼤似然估计仍为1X。
第7章参数估计----点估计一、填空题1、设总体X服从二项分布B(N,p),0P1,X1,X2X n是其一个样本,那么矩估计量p?XN.2、设总体X~B(1,p),其中未知参数0p1,X1,X2,X n是X的样本,则p的矩估计为_ 1n in1X i _,样本的似然函数为_in1X i(1p)1Xp__。
i3、设X1,X2,,X n是来自总体X~N(,2)的样本,则有关于及2的似然函数2L(X,X,X n;,)_12 in112e12(X) i22__。
二、计算题1、设总体X具有分布密度f(x;)(1)x,0x1,其中1是未知参数,X1,X2,X为一个样本,试求参数的矩估计和极大似然估计.n解:因E(X ) 1x1a()α1(α1)xdx1x dxαα112a2|xααα12令E(X)X?α?α122X1α?为的矩估计1Xn因似然函数L(x1,x2,x;)(1)(x1x2x)nnnlnLnln(α1)lnX,由αii1 l nLαnα 1inlnX0得,i1n ?的极大似量估计量为(1)αnln Xii12、设总体X服从指数分布f(x)xe,x00,其他,X1,X2,X n是来自X的样本,(1)求未知参数的矩估计;(2)求的极大似然估计.56解:(1)由于1 E(X),令11 X X,故的矩估计为? 1 X(2)似然函数nL(x,x,,x )e12ni nx i 1nlnLnlnxii1 ndlnLnnx0 indi1x ii1故的极大似然估计仍为1 X 。
3、设总体 2 X~N0,, X 1,X 2,,X n 为取自X 的一组简单随机样本,求 2 的极大似然估计;[解](1)似然函数n1 Le i122 x i 2 22n 22en 2x i 2 i 12于是n2nnx2i lnLln2ln2222i1 dlnLn1d224 22n i1 2x i,令 d lnL 2d 2 0,得的极大似然估计:n 122X ini1. 4、设总体X 服从泊松分布P(),X 1,X 2,,X n 为取自X 的一组简单随机样本,(1)求 未知参数估计;(2)求大似然估计. 解:(1)令E(X )X?X ,此为估计。