概率论 数理统计第16讲-1(王)

各章大体题详解习题一一、选择题1. （A ）A B A B B ⊂−−→=;（B ）B A A B A B B ⊂−−→⊂−−→=; （C ）AB A B A B B φ=−−→⊂−−→=;（D ）AB B A φ=−−→⊂ 不必然能推出A B B =（除非A B =）所以 选（D ）2. ()()()()()()()P A B P AB P AB P A P B P A P B -==--++ ()()()P A P B P AB =+-所以 选（C ）3. )()()()()()()()|(A P B P A P B P A P B P AB P B A P B A ≥−→−==−→−⊂所以 选（B ）4. 1)(0)()()()()(==−→−==B P A P B P A P AB P A P 或 所以 选（B ）5. （A ）若B A =，则φ=AB ，且φ==A A B A ，即B A ,不相容（B ）若φ≠⊃B A ，且Ω≠A ，则φ≠AB ，且φ≠=A B A ，即B A ,相容 （C ）若φφ≠=B A ,，则φ=AB ，且φ≠=B B A ，即B A ,相容 （D ）若φ≠AB ，不必然能推出φ=B A 所以 选（D ）6. （A ）若φ≠AB ，不必然能推出)()()(B P A P AB P =（B ）若1)(=A P ，且φ≠⊃B A ，则)()()()(B P A P B P AB P ==，即A,B 独立（C ）若φ=AB ，1)(0<<A P ,1)(0<<B P ，则)()()(B P A P AB P ≠ （D ）若1)(=A P ，则A 与任何事件都彼此独立 所以 选（B ）7. 射击n 次才命中k 次，即前1-n 次射击恰好命中1-k 次，且第n 次射击时命中目标，所以 选（C ）二、填空题8. C A C A C A A C A C A C A C A )())((= C C C C A A C C A C A C ==== ))(()()( 所以 C B =9. 共有44⨯种大体事件，向后两个邮筒投信有22⨯种大体事件，故所求概率为414422=⨯⨯ 10. 设事件A 表示两数之和大于21，则 样本空间}10,10|),{(<<<<=Ωy x y x ，}10,10,21|),{(<<<<>+=y x y x y x A 872121211=⋅⋅-==ΩS S P A 11. 由1.0)(,8.0)(=-=B A P A P ，得7.0)(=AB P ，故3.0)(=AB P 12. 由4.0)(,3.0)(,2.0)(===B A P B P A P ，得1.0)(=AB P ，故2.0)()()(=-=AB P B P A B P 13. 2.0)|()()(==A B P A P AB P ，故8.0)|()()(==B A P AB P B P14. )()()()()()()()(ABC P CA P BC P AB P C P B P A P C B A P +---++=)()()()()()()()()()()()(C P B P A P A P C P C P B P B P A P C P B P A P +---++=2719=15. 由于A,B 彼此独立，可得91)()()(==B P A P B A P ，)()(B A P B A P =，于是31)()(==B P A P ，故32)(=B P 三、计算题16.（1）)},,(),,,(),,,(),,,(),,,(),,,(),,,(),,,{(T T T H T T T H T H H T T T H H T H T H H H H H =Ω；（2）}3,2,1,0{=Ω；（3）}1|),{(22≤+=Ωy x y x ；（4）}5:0,5:1,5:2,5:3,5:4,4:5,3:5,2:5,1:5,0:5{=Ω 17.（1）C B A ； （2）)(C B A ； （3）C B A C B A C B A ； （4）AC BC AB ； （5）C B A ； （6）C B A ； （7）ABC18. 法一，由古典概率可知，所求概率为：2016420109⋅C ；法二，由伯努利定理可知，所求概率为：1644209.01.0⋅⋅C19. 只有唯一的一个六位数号码开能打开锁。

习题一：1.1 写出下列随机试验的样本空间：(1)某篮球运动员投篮时, 连续5 次都命中, 观察其投篮次数;解：连续5 次都命中，至少要投5次以上，故；(2)掷一颗匀称的骰子两次, 观察前后两次出现的点数之和;解：；(3)观察某医院一天内前来就诊的人数;解：医院一天内前来就诊的人数理论上可以从0到无穷，所以；(4)从编号为1，2，3，4，5 的5 件产品中任意取出两件, 观察取出哪两件产品;解：属于不放回抽样，故两件产品不会相同，编号必是一大一小，故：(5)检查两件产品是否合格;解：用0 表示合格, 1 表示不合格，则；(6)观察某地一天内的最高气温和最低气温(假设最低气温不低于T1, 最高气温不高于T2);解：用表示最低气温, 表示最高气温;考虑到这是一个二维的样本空间，故：；(7)在单位圆内任取两点, 观察这两点的距离;解：；(8)在长为的线段上任取一点, 该点将线段分成两段, 观察两线段的长度.解：；1.2(1)A 与B 都发生, 但C 不发生; ；(2)A 发生, 且B 与C 至少有一个发生;；(3)A,B,C 中至少有一个发生; ；(4)A,B,C 中恰有一个发生;；(5)A,B,C 中至少有两个发生; ；(6) A,B,C 中至多有一个发生;；(7) A;B;C 中至多有两个发生;(8) A,B,C 中恰有两个发生. ；注意：此类题目答案一般不唯一，有不同的表示方式。

1.3 设样本空间, 事件=,具体写出下列各事件：(1); (2) ; (3) ; (4)（1）；(2) =；(3) =;(4) =1.6 按从小到大次序排列, 并说明理由.解：由于故，而由加法公式，有：1.7解：(1) 昆虫出现残翅或退化性眼睛对应事件概率为：(2)由于事件可以分解为互斥事件，昆虫出现残翅, 但没有退化性眼睛对应事件概率为：(3) 昆虫未出现残翅, 也无退化性眼睛的概率为：.1.8解：(1) 由于，故显然当时P(AB) 取到最大值。

吴赣昌编 《概率论与数理统计》（理工类）三版课后习题解答习题1－31、袋中5个白球，3个黑球，一次任取两个。

（1）求取到的两个求颜色不同的概率；（2）求取到的两个求中有黑球的概率。

解：略2、10把钥匙有3把能打开门，今取两把，求能打开门的概率。

解:设A=“能打开”，则210S n C =法一，取出的两把钥匙，可能只有一把能打开，可能两把都能打开，则112373A n C C C =+ 所以()A Sn P A n = 法二，A ={都打不开}，即取得两把钥匙是从另7把中取得的，则27A n C =，所以27210()1()1C P A P A C =-=- 3、两封信投入四个信筒，求（1）前两个信筒没有信的概率，（2）第一个信筒内只有一封信的概率。

解：24S n =（两封信投入四个信筒的总的方法，重复排列）（1）设A=“前两个信筒没有信”，即两封信在余下的两个信筒中重复排列，22A n =；（2）设B=“第一个信筒内只有一封信”，则应从两封信中选一封放在第一个信筒中，再把余下的一封信放入余下的三个信筒中的任一个，1123B n C =带入公式既得两个概率。

4、一副扑克牌52张，不放回抽样，每次取一张，连续抽4张，求花色各异的概率.解：略5、袋中有红、黄、黑色求各一个，有放回取3次，求下列事件的概率。

A=“三次都是红球”；B=“三次未抽到黑球”，C=“颜色全不相同”，Ｄ＝“颜色不全相同” 解：略6、从0,1,2,,9L 等10个数字中，任意选出不同的三个数字，试求下列事件的概率：1A =‘三个数字中不含0和5’，2A =‘三个数字中不含0或5’，3A =‘三个数字中含0但不含5’.解 3813107()15C P A C ==. 333998233310101014()15C C C P A C C C =+-=， 或 182231014()1()115C P A P A C =-=-=， 2833107()30C P A C ==. 7、从一副52张的扑克牌中任取3张，不重复，计算取出的3张牌中至少有2张花色相同的概率。

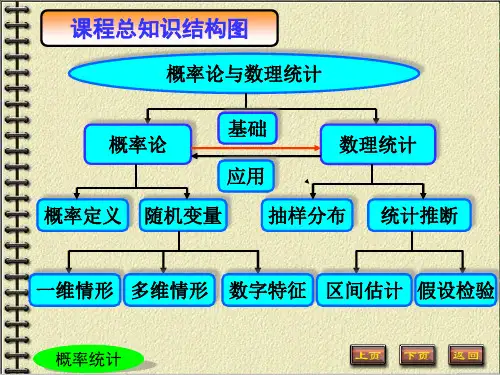
考研数学问题咨询张伟老师新浪微博张伟老师仰望星空E-mail: zwpku@参考教材概率论与数理统计第四版（浙江大学主编）重要定理、性质、公式、结论经典例题、重要例题及不需要做的题目第一章概率论的基本概念（考小题）第一节随机试验（了解）第二节样本空间，随机事件（了解）第三节频率与概率（频率可以不用看，了解）第四节等可能概率（古典概论）（难点非重点，做一些基本题即可）第五节条件概率（重要，考小题为主，考大题有时会用到）第六节独立性（重要，考小题为主，大题经常会用到）第二章随机变量及其分布（至少考小题，考大题一定会用到）第一节随机变量（了解）第二节离散型随机变量及其分布律（重要，经常考）第三节随机变量的分布函数（重要，每年必考）第四节连续型随机变量及其概率密度（重要，每年必考）第五节随机变量的函数分布（重要，大题的命题点）第三章多维随机变量及其分布（考大题可能性极大）第一节二维随机变量（了解）第二节边缘分布（理解）第三节条件分布（理解）第四节概率独立的随机变量（重要，基本每年必考）第五节两个随机变量函数的分布（重要，大题的经典命题点）第四章随机变量的数字特征（重要）第一节数学期望（重要，每年必考）第二节方差（重要，每年必考）第三节协方差与相关系数（重要，经常考）第四节矩，协方差矩阵（矩，了解，协方差矩阵不用看）.第五章大数定律及中心极限定理(了解)第一节大数定律(了解,关注定律的前提条件与结论)第二节中心极限定理（了解，关注定理的前提条件与结论）考研数学问题咨询张伟老师新浪微博张伟老师仰望星空E-mail: zwpku@第六章样本及抽样分布（考小题为主）第一随机样本（了解，其中有重要概念，简单随机样本）第二直方图和箱线图（重要，考小题）第三抽样分布（重要，考小题）第七章参数估计（重要，考大题经典章节）第一节点估计（极其重要，矩估计：重点非难点，最大似然估计（重点且难点））第二节基于截尾样本的最大似然估计（不用看）第三节估计量的评选标准（数一重要，数三不用看）第四区间估计（数一理解，考的比较少）第五正态总体均值与方差的区间估计（数一理解，考的比较少）第六（０－１）分布参数的区间估计（不用看）第七单侧置信区间（理解，一般不考）（第四－第七，只有数一考，数三均不用看）第八章假设检验（理解，一般不考，只有数一有要求，数三不考）第一假设检验（理解）第二正态总体均值的假设检验（理解）第三正态总体方差的假设检验（理解）第四，第五，第六，第七，第八（均不用看）．考研数学问题咨询张伟老师新浪微博张伟老师仰望星空E-mail: zwpku@考研数学概率统计的重点难点必考点及重要例题和习题不用做的例题和习题第一章概率论的基本概念P３最后４行的小写字体不用看P５例３不用做（一）频率不用看P6-7 例 1 与例 2 均不用做，P7 概率重点看P9 等可能概率一般都不单独考，考大题经常会用到，P13 例 6 不用做，P14 例 8 不用做 P14 条件概率重点看，P15 例 2 不用做，P16 例 3 不用做，P17 例 4 重点做P17（三）全概率公式和贝叶斯公式为难点P19例5不用做，P20独立性为考研数学的绝对重点，P22例2与例3均不用做P23例4重点做P24-29 不用做的习题是 1、5、6、10、12、15、16、18、19、20、21、23、25、26、29、32、34、35、38、39、40第二章随机变量及其分布P30 例 1 不用看P37 泊松定理只需要记住结论，证明可以不用看P38 随机变量的分布函数为考研必考概念P42 连续性随机变量概率密度为考研必考点P50 随机变量的函数的分布是考大题的重要命题点P53 例 5 不用做P55-59 不用做的习题 1、5、6、7、9、10、11、13、15、16、19、22、27、28、30、31、38、39第三章多位随机变量及其分布P63 性质 4 的解释不用看P65 例 1 不用做，P66 例 3 重点做一下（提升计算能力）P68 例 1 不用做，P72 相互独立的随机变量为重点章节P76 两个随机变量的函数的分布为考大题的重要备考章节P78 例 3 不用做，P81 例 5 不用做P84-89 不用做的习题是 3、6、7、10、11、12、13、28、31第四章随机变量的数字特征P91 例 1 不用做，P92 例 3 与例 4 不用做，P93 例 5 不用做P95 中间的证明不用看，P96 例 8 与例 10 不用做P97 例 11 不用做，P100 例 13 不用做，P105 不用做P107 XY的两条重要性质的推导及含义不用看考研数学问题咨询张伟老师新浪微博张伟老师仰望星空E-mail: zwpku@考研数学问题咨询张伟老师新浪微博张伟老师仰望星空E-mail: zwpku@P108 只需要看前四行即只需要记住定理 4 证明可以不用看P109 例 2 重点做（提升计算能力）P110 矩为一般考点，协方差矩阵不用看P113-118 不用做的习题是 1.4.5.12.13.15.16.18.19.22.23.24.35.36.37.38第五章大数定律及中心极限定理（难点非重点）P124 例 1 不用做P126-127 不用做的习题是 2、4、5、10、11、13第六章样本及抽样分布（一般考点考小题）P130 第四行简单随机样本为重要概念P130 第二节直方图和箱线图不用看P135 第三节抽样分布（考小题），P136 统计量定义及几个常见统计量要重点看而且要牢记其表达式P137 经验分布函数只有数三同学稍微了解P138-141 数理统计所有的三大分布的典型模式要牢记但三种分布的概率密度表达式可以不用记P145-147 定理 2 的证明与推广均不用看P147-148 不用做的习题是 1、5、6、10、11第七章参数估计（数一数三的绝对的重点和难点）P149 点估计数一数三的绝对重点矩估计重点非难点，最大似然估计重点且难点P163-155 例 4 例 5 例 6 重点做P156-158 第二节基于截尾样本的最大似然估计不用看P158 估计量的评选标准数一重点看，数三大纲上虽然没有但建议数三看一下最好P161-168 区间估计，正态总体均值与方差的区间估计，只有数一看，为一般考点P168 0-1 分布参数的区间估计数一数三均不用看P169 单侧置信区间，只有数一看，为一般考点P193-177 数三不用做的习题为 4（3）、6、7、8、9、10、11-27 均不用做数一不用做的习题为4（3）、6、7、8、9、15、17、20、21、22、23、26、27第八章假设检验（数一特有的考点，难点非重点）数一只需要看前四节P178-193从第五节以后均不需要看P218-223 习题只需要做 1、2、3、4 其余的题目可以不用做考研数学问题咨询张伟老师新浪微博张伟老师仰望星空E-mail: zwpku@。

《概率论与数理统计》课程教学大纲课程中英文名称：概率论与数理统计(Probability and Statistics)课程代码：课程类别：必修课；一年级；二年级；公共类数学基础课学分/学时：3学分/51学时开课学期：适用专业：先修/后修课程：高等数学(或微积分)开课单位：课程负责人：1、课程性质与教学目标概率论与数理统计是研究随机现象客观规律并付诸应用的数学类学科，是工科本科各专业的一门重要基础理论课，通过本课程的学习，要求学生熟练掌握随机事件概率的常用计算方法，熟悉并掌握随机变量的分布及其计算，掌握离散型随机变量及其分布律的概念及其计算、掌握连续型随机变量及其密度函数的概念及其计算。

掌握随机变量的常用数字特征的概念及其计算。

理解并掌握依概率收敛的概念，理解大数定律、理解并掌握用中心极限定理解决应用问题。

理解和掌握数理统计的基本概念和理论、熟悉常用的统计量和抽样分布，熟悉并掌握常用的参数点估计和置信区间的求解。

掌握假设检验的基本概念、理解检验中的两类风险，理解并掌握显著性检验的基本步骤，掌握正态总体下未知参数的假设检验方法并会用于解决实际问题，了解拟合优度检验和独立性检验等非参数检验方法。

通过本课程的学习，使学生具备以下能力：课程教学目标1：有科学的世界观、人生观和价值观，有责任心和社会责任感。

树立远大的理想以及刻苦学习的信念。

课程教学目标2：使学生掌握概率统计的基本概念、基本思想和基本理论，培养学生用所学知识去分析问题和解决问题的综合能力和高级思维能力。

课程教学目标3：促进学生全面发展；打破习惯性认知模式，培养学生深度分析、大胆质疑、勇于创新的能力；引导学生养成自主学习、终身学习的自我管理素养。

2、教学内容及基本要求本课程教学内容与具体教学要求及学时分配等信息如下表所示。

3、教学方法课堂教学以板书为主，辅助PPT。

4、考核、成绩评定方式及重修要求考核方式主要由上课出勤、平时作业、课堂练习、阶段测验、期末考试等环节组成，综合各部分的成绩给出该门课程的总评成绩。