下载文档原格式
工作报告-叠加原理和戴维南定理实验报告工作报告-叠加原理和戴维南定理实验报告一、实验目的1.学习和掌握叠加原理和戴维南定理的基本概念和原理。
2.通过实验，深入理解叠加原理和戴维南定理的实际应用。
3.提高实验技能和动手能力，掌握基本的电路分析和设计方法。
二、实验原理1.叠加原理：在线性电路中，多个电源共同作用时，各电源单独作用产生的电压（或电流）之和等于它们共同作用时产生的电压（或电流）。
2.戴维南定理：任何一个有源二端网络，都可以等效为一个电源电动势E和内阻R串联的形式。
其中，电动势E等于开路电压，内阻R等于网络中所有电源为零时，从两端看向网络的等效电阻。
三、实验步骤1.准备实验器材：电源、电阻器、电压表、电流表、电键、导线等。
2.搭建实验电路：根据叠加原理和戴维南定理的原理，搭建相应的电路。
3.进行实验测量：首先，分别测量各电源单独作用时的电压（或电流）；然后，同时作用时测量总的电压（或电流）。
4.分析实验数据：根据测量数据，验证叠加原理的正确性，并根据戴维南定理计算等效电动势和内阻。
5.讨论实验结果：对实验结果进行分析和讨论，评估误差和实验条件的影响。
四、实验结果及分析1.数据记录：2.结果分析：通过实验测量，我们发现总电压（15V）等于三个电源电压之和（10V + 5V + 8V = 23V），总电流（4.5A）也等于三个电源电流之和（2A + 1A +1.5A = 4.5A），验证了叠加原理的正确性。
同时，根据戴维南定理，等效电动势E等于开路电压（15V），等效内阻R等于网络中所有电源为零时，从两端看向网络的等效电阻。
在这个实验中，由于只有一个电阻器，所以等效内阻R等于该电阻器的阻值。
五、结论总结通过本次实验，我们验证了叠加原理和戴维南定理的正确性，并掌握了它们的实际应用。
实验结果表明，在线性电路中，多个电源共同作用时，各电源单独作用产生的电压（或电流）之和等于它们共同作用时产生的电压（或电流），这为分析和设计电路提供了重要的理论依据。
叠加定理和戴维南定理实验报告实验报告：叠加定理和戴维南定理
引言：
在本次实验中, 我们将介绍和应用叠加定理和戴维南定理两个电路原理的实验过程、结果和分析。
材料和方法:
我们使用了电流计，电压计和万用表等电学实验工具，以及运用不同的电路仿真软件如Multisim、Simetrix等，并采取多种电路组合，对系统进行测试。
结果和分析：
通过本次实验，我们可以看出叠加定理是一种简单但有效的方法，在测量复杂电路时能够快速轻松地计算出每个单独的电流和电压。
另一方面，戴维南定理可以使我们更有效地使用材料和设备，以及识别更重要的电路部分。
结论：
总的来说，本次实验是成功的。
通过应用叠加定理和戴维南定理，我们得出了精确的电路参数，测试结果符合预期，证明了这两个电路原理在电路设计中的重要性和实用性。
未来展望：
本次实验对我们进一步深入研究电路设计和电路优化提供了很好的基础。
我们还可以在此基础上，尝试更复杂的电路设计和实验，进一步加强我们的实践能力。
叠加定理和戴维南定理实验报告一、实验目的1、深入理解叠加定理和戴维南定理的基本概念和原理。
2、通过实验操作，掌握运用叠加定理和戴维南定理分析电路的方法。
3、培养实验操作技能和数据处理能力，提高对电路理论的实际应用能力。
二、实验原理1、叠加定理叠加定理指出：在线性电路中，多个电源共同作用时，在任一支路中产生的电流（或电压）等于各个电源单独作用时在该支路产生的电流（或电压）的代数和。
在使用叠加定理时，需要分别考虑每个电源单独作用的情况。
当一个电源单独作用时，其他电源应视为零值，即电压源短路，电流源开路。
然后将各个电源单独作用时在该支路产生的电流（或电压）进行代数相加，得到最终的结果。
2、戴维南定理戴维南定理表明：任何一个线性有源二端网络，对外电路来说，可以用一个电压源和一个电阻的串联组合来等效替代。
其中，电压源的电压等于有源二端网络的开路电压，电阻等于有源二端网络内所有独立电源置零后所得到的无源二端网络的等效电阻。
三、实验设备1、直流稳压电源（多组输出）2、直流电流表3、直流电压表4、电阻箱5、实验电路板6、连接导线若干四、实验内容与步骤1、叠加定理实验（1）按照图 1 所示连接电路，其中 E1 ＝ 10V，E2 ＝ 5V，R1 ＝10Ω，R2 ＝20Ω，R3 ＝30Ω。
（2）测量 E1 单独作用时，各支路的电流和电压。
将 E2 短路，接通 E1，记录电流表和电压表的读数。
（3）测量 E2 单独作用时，各支路的电流和电压。
将 E1 短路，接通 E2，记录电流表和电压表的读数。
（4）测量 E1 和 E2 共同作用时，各支路的电流和电压。
同时接通E1 和 E2，记录电流表和电压表的读数。
（5）将测量结果填入表 1，验证叠加定理。
表 1 叠加定理实验数据｜电源作用情况｜ I1（mA）｜ I2（mA）｜ I3（mA）｜ Uab （V）｜｜｜｜｜｜｜｜ E1 单独作用｜＿___ ｜＿___ ｜＿___ ｜＿___ ｜｜ E2 单独作用｜＿___ ｜＿___ ｜＿___ ｜＿___ ｜｜ E1、E2 共同作用｜＿___ ｜＿___ ｜＿___ ｜＿___ ｜｜叠加结果｜＿___ ｜＿___ ｜＿___ ｜＿___ ｜2、戴维南定理实验（1）按照图 2 所示连接电路，其中有源二端网络由电阻 R1 ＝50Ω，R2 ＝100Ω，电压源 E ＝ 20V 组成。
叠加原理和戴维南定理叠加原理和戴维南定理，这俩名字听起来是不是有点高大上？但其实它们就像是电路世界里的小道消息，平时没什么人关注，但一旦你掌握了，就能在电路中游刃有余。
想象一下，咱们在电路中就像是在参加一场热闹的派对，每个电流、每个电压都是派对上的嘉宾。
叠加原理就像是邀请你，把不同的嘉宾分开，单独来看看每个人的表现。
你可以先把电路里的各个电源一个个拿出来，看看每个电源带来的电流和电压。
再把这些结果“叠加”在一起，就能看到整个电路的精彩面貌。
说白了，就是把复杂的事简单化，像是把一桌子的菜分成几个小盘子，先尝一口再说。
咱们再聊聊戴维南定理。
这个定理就像是电路的“简化大师”。
想象你在厨房里做菜，原本材料多得不得了，让人眼花缭乱。
可是戴维南定理就好比是一个神奇的调料，让你把这些复杂的材料简化成一个单一的“美味”。
它告诉你，不管电路多复杂，最终你都可以把它变成一个电压源加上一个电阻的组合。
就像是把一场复杂的宴会，变成一个简单的聚餐，只需几道经典菜就能满足大家。
这样你就能轻松计算出电流和电压，不再被复杂的电路搞得头晕脑胀。
说到这里，可能有人会问，这些定理到底有什么用？别着急，咱们慢慢来。
叠加原理就像是让你能分开来看每个电源的“功劳”。
比如，想象一下你的手机充电器，里面可能有好几个电源同时工作。
用叠加原理，你可以把每个电源的贡献都算出来，知道哪一个最给力，哪一个稍微逊色。
这样你就能更好地调整电路，提升整体性能，真是一举多得。
然后，戴维南定理的妙处就更不用说了。
想想看，生活中总是会遇到各种各样的复杂问题。
一道难题让你绞尽脑汁，结果却发现，经过简化，问题变得简单明了。
就像是在追求完美的同时，忽略了简单的快乐。
电路也是如此，很多时候，我们在追求复杂的电路设计时，反而忘记了简单的解决方案。
戴维南定理正好给了我们这个灵感，提醒我们在复杂中寻找简单。
再说说实际应用，叠加原理和戴维南定理在电力工程、电子设计等领域那是相当重要的工具。
实验4叠加原理与戴维南定理的验证实验四叠加原理与戴维南定理的验证⼀、实验⽬的1、验证线性电路叠加原理的正确性，加深对线性电路的叠加性和齐次性的认识和理解。
2、验证戴维南定理的正确性3、掌握测量有源⼆端⽹络等效参数的⼀般⽅法⼆、原理说明1、叠加原理：在有⼏个独⽴源共同作⽤下的线性电路中，通过每⼀个元件的电流或其两端的电压，可以看成是由每⼀个独⽴源单独作⽤时在该元件上所产⽣的电流或电压的代数和。
线性电路的齐次性是指当激励信号（某独⽴源的值）增加或减⼩K倍时，电路的响应（即在电路其它各电阻元件上所建⽴的电流和电压值）也将增加或减⼩K倍。
2、任何⼀个线性含源⽹络，如果仅研究其中⼀条⽀路的电压和电流，则可将电路的其余部分看作是⼀个有源⼆端⽹络（或称为含源⼆端⼝⽹络）。
戴维南定理指出：任何⼀个线性有源⽹络，总可以⽤⼀个等效电压源来代替，此电压源的电动势E S等于这个有源⼆端⽹络的开路电压U0C，其等效内阻R0等于该⽹络中所有独⽴源均置零（理想电压源视为短路，理想电流视为开路）时的等效电阻。
U0C和R0称为有源⼆端⽹络的等效参数。
3、有源⼆端⽹络等效参数的测量⽅法（1）开路电压、短路电流法在有源⼆端⽹络输出端开路时，⽤电压表直接测其输出端的开路电压U0C，然后将其输出端短路，⽤电流表测其短路电流I SC，则内阻为R0=U OC/I SC（2）伏安法⽤电压表、电流表测出有源⼆端⽹络的外特性如图A所⽰。
根据外特性曲线求出斜率tgΦ，则内阻R O=tgΦ=△U/△I=U OC/I SC图A 图B⽤伏安法，主要是测量开路电压及电流为额定值I N时的输出端电压值U N，则内阻为R O=U OC-U N/I N若⼆端⽹络的内阻值很低短路电流很⼤时，则不宜测短路电流。
（3）半电压法如图B所⽰，当负载电压为被测⽹络开路电压⼀半时，负载电阻（负载电阻由万⽤表测量），即为被测有源⼆端⽹络的等效内阻值。
（4）零⽰法在测量具有⾼内阻有源⼆端⽹络的开路电压时，⽤电压表进⾏直接测量会造成较⼤的误差，为了消除电压表内阻的影响，往往采⽤零⽰测量法，如图C所⽰。
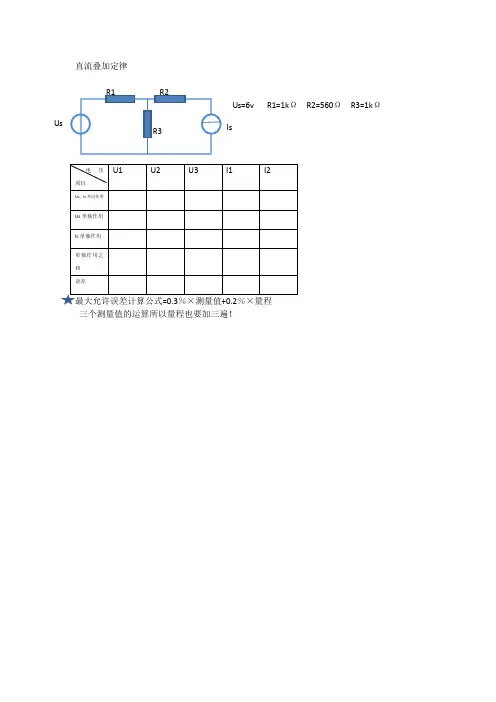
直流叠加定律
Us=6v R1=1k Ω R2=560Ω R3=1k Ω
电
压 项目
U1 U2 U3 I1 I2 Us 、Is 共同作用
Us 单独作用
Is 单独作用
单独作用之和
误差
最大允许误差计算公式=0.3％×测量值+0.2％×量程
三个测量值的运算所以量程也要加三遍！
R1
R2 Is R3
Us
戴维南、诺顿定理
首先是有源线性一端口网络等效参数Req 、Uoc 的测量
三种方法：开路、短路法
半电压法
两点法
开路、短路法：
测量 开路电压Uoc=
短路电流Is=
计算 等效内阻Req=Uoc/Is=
半电压法：
测得Uoc 后接可变电阻作为Rl ，同时测其两端电压U,调节Rl 使U=Uoc/2,则Rl=Req
两点法：
负载取两不同值，△U/△I=Req
然后是等效电路连接，通过比较流过负载的ＩL 、ＩL ’验证定理的正确性
诺顿定理亦然
误差分析
最大允许误差△Req=(△Um/Uoc+△Im/Isc)Uoc/Isc
△Um 、△Im 分别为电压表和电流表的最大允许误差即0.3％×测量值+0.2％×量程 1k Ω 2k Ω 2k Ω Rl E=6v E Req ＩL Rl ＩL ’ Rl Is
Ro。
戴维南定理和叠加定理的区别《戴维南定理和叠加定理的区别》戴维南定理和叠加定理是电路分析中常用到的两个重要定理，它们都提供了简化电路分析的方法。
然而，尽管它们都是用于解决电路问题的工具，但每个定理都有其独特的应用和适用范围。
首先，让我们来看看戴维南定理。
戴维南定理（Thevenin's theorem）是基于线性电路理论的一种分析方法。
该定理断言任何线性两端口或多端口网络都可以等效为一个等效电压源与一个等效电阻的串联电路。
简而言之，它能够将复杂的线性电路简化成一个更容易分析的等效电路。
戴维南定理的关键思想是将复杂的电路分解为两个主要部分：一个等效电压源（Thevenin电压源）和一个等效电阻（Thevenin电阻）。
等效电压源等于原始电路在被视为负载时的开路电压，而等效电阻则等于原始电路视角下的内部电阻。
与戴维南定理相比，叠加定理（Superposition theorem）则更适用于解决非线性电路问题。
叠加定理的核心思想是将电路的各个独立源（例如电压源或电流源）单独激发，并将其他源视为关闭状态。
然后，通过叠加每个激发的结果，最终得到电路的总体响应。
叠加定理的一个关键限制是，它仅适用于线性电路。
这是因为叠加定理基于电路的线性特性，而非线性元件，如二极管和晶体管，则无法使用叠加定理进行分析。
另一个区别是在使用方法上。
在戴维南定理中，我们需要计算电路的等效电压源和等效电阻，并将它们串联在一起。
这样就能够将原电路简化为一个等效电路。
而叠加定理则需要对每个源进行独立激发，并将其他源视为关闭状态。
然后，通过计算每个源激发时的响应，并将它们求和，最终可以得到电路的总体响应。
总而言之，戴维南定理和叠加定理在电路分析中都扮演着重要的角色。
戴维南定理适用于线性电路的简化分析，而叠加定理则适用于线性电路的响应计算。
通过正确理解和应用这两个定理，我们可以更轻松地解决各种电路问题。
叠加定理和戴维南定理实验报告在物理学中，叠加定理和戴维南定理是两个非常重要的概念，它们在解决复杂物理问题时起着至关重要的作用。
本实验旨在通过具体的实验操作，验证叠加定理和戴维南定理，并对其原理进行深入的探究和分析。
实验一，验证叠加定理。
首先，我们将在实验室中准备好一个平行板电容器，然后分别将两块不同电介质板插入电容器中。
接下来，我们将连接电源，使电容器充电，然后使用电场强度计测量不同电介质板间的电场强度。
通过实验数据的记录和分析，我们可以验证叠加定理在电场叠加方面的准确性。
实验二，验证戴维南定理。
在这个实验中，我们将使用弹簧振子系统来验证戴维南定理。
首先，我们将测量单个弹簧振子的振动周期和频率，然后将两个弹簧振子连接在一起，再次测量其振动周期和频率。
通过对比实验数据，我们可以验证戴维南定理在多个振动系统叠加时的准确性。
实验结果分析：通过以上两个实验的操作和数据分析，我们得出了以下结论，叠加定理和戴维南定理在实验中得到了有效验证。
叠加定理表明，对于线性介质，所受外电场的合成效应等于各个电场单独作用时的效应之和；戴维南定理则表明，多个振动系统叠加时，每个振动系统的振幅和相位都可以分别求出，然后再将它们进行矢量叠加。
结论：通过本次实验，我们验证了叠加定理和戴维南定理的准确性，这两个定理在物理学中有着广泛的应用。
它们为我们解决复杂的物理问题提供了重要的理论基础，对于深入理解电场、振动系统等物理现象具有重要意义。
总结：叠加定理和戴维南定理是物理学中的重要概念，通过本次实验，我们对这两个定理有了更深入的理解。
这些理论知识的实际应用，不仅帮助我们解决了具体的物理问题，也为我们打开了更广阔的物理世界。
通过不断的实验探究和理论学习，我们可以更好地理解和应用这些重要的物理定律。
