电阻、叠加定理和戴维南习题

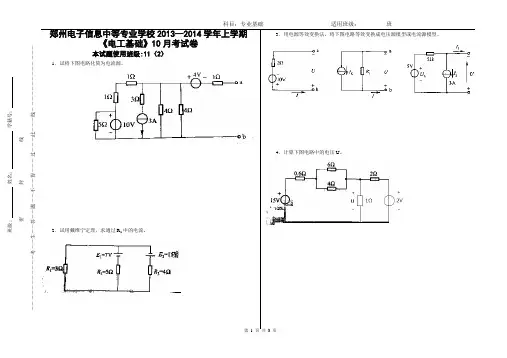
科目：专业基础 适用班级： 班班级： 姓名： 学籍号：----------------------------------------------------密-------------------封----------------------线------------------------------------------------------―――――――――――考――生――答――题――不――得―――过―――此―――线―――――――――――――郑州电子信息中等专业学校2013—2014学年上学期《电工基础》10月考试卷本试题使用班级:11（2）1．试将下图电路化简为电流源。

2．试用戴维宁定理，求通过R 1中的电流。

3．用电源等效变换法，将下图电路等效变换成电压源模型或电流源模型。

4．计算下图电路中的电压U 。

班级： 姓名： 学籍号：----------------------------------------------------密-------------------封----------------------线------------------------------------------------------ ―――――――――――考――生――答――题――不――得―――过―――此―――线―――――――――――――5．已知下图电路中，Us 1＝Us 2＝10V ，R 1＝R 2＝R 3=10欧，试用戴维宁定理求I 3。

6．将下图化为最简形式7．求下图所示电路中的电流I 。

8．如下图，已知Us 1=40V ，Us 2=20V ，Us 3=18V ，R 1=4欧，R 2=2欧，R 3＝3欧，试用支路电流法求解各支路上的电流。

班级： 姓名： 学籍号：----------------------------------------------------密-------------------封----------------------线------------------------------------------------------ ―――――――――――考――生――答――题――不――得―――过―――此―――线―――――――――――――9．求下图ab 间的电压。

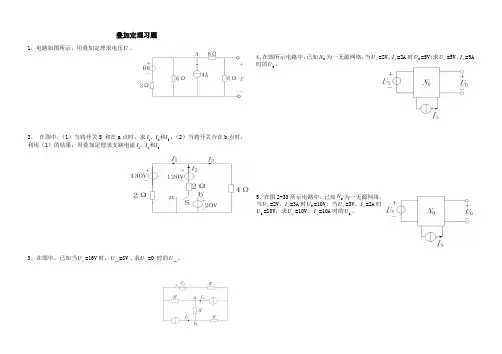
叠加定理习题1、电路如图所示，用叠加定理求电压U 。

2、 在图中，（1）当将开关S 和在a 点时，求123I I I 、和；（2）当将开关合在b 点时，利用（1）的结果，用叠加定理求支路电流123I I I 、和3、在图中，已知当S U =16V 时，ab U =8V ,求S U =0 时的ab U 。

4、在图所示电路中，已知0N 为一无源网络，当S U =2V 、S I =2A 时0U =5V;求S U =5V 、S I =5A 时的0U 。

5、在图2-33所示电路中，已知0N 为一无源网络，当S U =2V 、S I =3A 时0U =10V; 当S U =3V 、S I =2A 时0U =10V ，求S U =10V 、S I =10A 时的0U 。

弥尔曼定理习题1、求如图所示电路中的电流i。

2、求如图电路中A点的电位。

3、求图所示电路中的各支路电流，并计算2 电阻吸收的功率。

A6Ω8A 12V3Ω2Ω6V6ΩB+-+-I1I2I34、求如图所示电路中的支路电流I1、I2、I3。

5、如图所示电路中，E1=12V，E2=30V，I S=2A，R1=3Ω，R2=6Ω，求I1、I2。

6、电路如图所示，求各支路电流。

7、如图所示电路，求出各支路电流。

网孔电流法习题1、图示电路，已知E1 = 42 V，E2 = 21 V，R1 = 12 Ω，R2 = 3 Ω，R3 = 6 Ω，求各支路电流I1、I2、I3 。

2、求解电路中各条支路电流3、试用网孔电流法求如图所示电路中的支路电流I1、I2、I3。

4、如图所示电路中，U S=10V，I S=2A，R1=10Ω，R2=50Ω，R3=2Ω，R4=8Ω，用网孔电流法求I1、I2、I3。

5、如图所示电路，求出各支路电流。

6、电路如图所示，求各支路电流。

戴维宁定理习题1、在图所示的电路中，分别用戴维宁定理求电流LI。

2、电路如图所示，（1）用戴维宁定理求电阻RL 中的电流IL；（2）若RL为可变电阻，求R L 获得的最大功率及此时的RL值。

电路第4章习题集电路定理第4章电路定理4-1XX 简单题4-2XX 叠加定理4-3XX 戴维宁定理4-201、试用叠加定理计算下图所示电路中US2=2V时，电压U4的大小。

若US1的大小不变，要使U4=0，则US2应等于多少？答案 U4=-0.4V, Us2=1.2V4-202、电路如图所示。

（1）用叠加定理求各支路电流；（2）求电压源发出的功率。

答案 I1=-50mA, I2=15mA, I3=60mA (2)电压源发出的功率为：P=25I1=-1.25W4-204、4-205、求题3-22图示电路的电压U和电流I。

+-2I110V+-3A-+ U4Ω6Ω9ΩI1题3-22图I例4－4 用叠加定理求图4－5(a)电路中电压u。

图4－5解：画出独立电压源u S和独立电流源i S单独作用的电路，如图(b)和(c)所示。

由此分别求得u’和u”,然后根据叠加定理将u’和u”相加得到电压u4-206、例4－1 利用叠加定理求图（a ）所示电路中的电压U 。

（a ） (b) (c)解：首先画出分电路图如图(b)、(c)所示。

当12V 电压源作用时，应用分压原理有：V 43912)1(-=⨯-=U 当3A 电流源作用时，应用分流公式得：V 633636)2(=⨯+⨯=U 则所求电压：V 264=+-=U4-207、例4－2利用叠加定理求图（a ）所示电路中的电压u 和电流i 。

（a ） (b) (c)解：首先画出分电路图如图(b)、(c)所示。

当 10V 电源作用时：)12/()210()1()1(+-=i i 解得：A i 2)1(=，V i i i u 6321)1()1()1()1(==+⨯=当5A 电源作用时，由左边回路的KVL ：02)5(12)2()2()2(=++⨯+i i i 解得：A i 1)2(-=，V i u 22)2()2(=-= 所以： V u u u 8)2()1(=+= A i i i 1)2()1(=+=注意：受控源始终保留在分电路中。

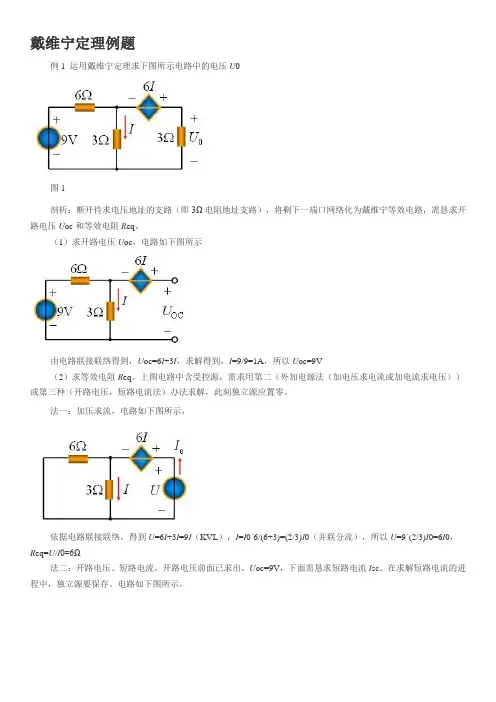
戴维宁定理例题例1 运用戴维宁定理求下图所示电路中的电压U0图1剖析：断开待求电压地址的支路（即3Ω电阻地址支路），将剩下一端口网络化为戴维宁等效电路，需恳求开路电压U oc和等效电阻R eq。

（1）求开路电压U oc，电路如下图所示由电路联接联络得到，U oc=6I+3I，求解得到，I=9/9=1A，所以U oc=9V（2）求等效电阻R eq。

上图电路中含受控源，需求用第二（外加电源法（加电压求电流或加电流求电压））或第三种（开路电压，短路电流法）办法求解，此刻独立源应置零。

法一：加压求流，电路如下图所示，依据电路联接联络，得到U=6I+3I=9I（KVL），I=I0´6/(6+3)=(2/3)I0（并联分流），所以U=9´(2/3)I0=6I0，R eq=U/I0=6Ω法二：开路电压、短路电流。

开路电压前面已求出，U oc=9V，下面需恳求短路电流I sc。

在求解短路电流的进程中，独立源要保存。

电路如下图所示。

依据电路联接联络，得到6I1+3I=9（KVL），6I+3I=0（KVL），故I=0，得到I sc=I1=9/6=1.5A（KCL），所以R eq=U oc/I sc=6Ω终究，等效电路如下图所示依据电路联接，得到留心：核算含受控源电路的等效电阻是用外加电源法仍是开路、短路法，要详细疑问详细剖析，以核算简练为好。

戴维南定理典型例子戴维南定理指出，等效二端网络的电动势E等于二端网络开路时的电压，它的串联内阻抗等于网络内部各独立源和电容电压、电感电流都为零时，从这二端看向网络的阻抗Zi。

设二端网络N中含有独立电源和线性时不变二端元件（电阻器、电感器、电容器），这些元件之间可以有耦合，即可以有受控源及互感耦合；网络N的两端ɑ、b接有负载阻抗Z（s），但负载与网络N内部诸元件之间没有耦合，U（s）=I（s）/Z（s）。

当网络N中所有独立电源都不工作（例如将独立电压源用短路代替，独立电流源用开路代替），所有电容电压和电感电流的初始值都为零的时候，可把这二端网络记作N0。

第四章电路定理◆重点：1、叠加定理2、戴维南定理和诺顿定理◆难点：1、熟练地运用叠加定理、戴维南定理和诺顿定理分析计算电路。

2、掌握特勒根定理和互易定理，理解这两个定理在路分析中的意义。

4-1 叠加定理网络图论与矩阵论、计算方法等构成电路的计算机辅助分析的基础。

其中网络图论主要讨论电路分析中的拓扑规律性，从而便于电路方程的列写。

4.1.1 几个概念1．线性电路——Linear circuit由线性元件和独立源组成的电路称为线性电路。

2．激励与响应——excitation and response在电路中，独立源为电路的输入，对电路起着“激励”的作用，而其他元件的电压与电流只是激励引起的“响应”。

3．齐次性和可加性——homogeneity property and additivity property“齐次性”又称“比例性”，即激励增大K倍，响应也增大K倍；“可加性”意为激励的和产生的响应等于激励分别产生的响应的和。

“线性”的含义即包含了齐次性和可加性。

齐次性：可加性：4.1.2 叠加定理1．定理内容在线性电阻电路中，任一支路电流（电压）都是电路中各个独立电源单独作用时在该支路产生的电流（电压）之叠加。

此处的“线性电阻电路”，可以包含线性电阻、独立源和线性受控源等元件。

2．定理的应用方法将电路中的各个独立源分别单独列出，此时其他的电源置零——独立电压源用短路线代替，独立电流源用开路代替——分别求取出各独立源单独作用时产生的电流或电压。

计算时，电路中的电阻、受控源元件及其联接结构不变。

4.1.3 关于定理的说明1．只适用于线性电路2．进行叠加时，除去独立源外的所有元件，包含独立源的内阻都不能改变。

3．叠加时应该注意参考方向与叠加时的符号4．功率的计算不能使用叠加定理4.1.4 例题1．已知：电路如图所示–6V+4– 6V +求：X U 及两个独立源和受控源分别产生的功率。

解：根据叠加定理，电路中电压源和电流源分别作用时的电路如图（b ）、（c ）所示。

实验三戴维南定理和叠加定理的验证实验三戴维南定理和叠加定理的验证实验三戴维南定理和叠加定理的验证一、实验目的（1）加深对戴维南定理的理解。

(2)学习戴维南等效参数的各种测量方法。

(3)理解等效置换的概念。

（4）通过实验加深对叠加定理的理解。

（5）研究了叠加定理的适用范围和条件。

(6)学习直流稳压电源、万用表、直流电流表和电压表的正确使用方法。

二、实验原理及说明1.戴维南定理是指具有独立电源、线性电阻和受控源的端口。

对于外部电路，可以用电压源和电阻的串联组合来代替。

该电压源的电压等于端口的开路电压UOC，该电阻等于端口的所有独立电源设置为零后的输入电阻，如图2.3-1所示。

这种电压源和电阻的串联组合称为戴维南等效电路。

等效电路中的电阻称为戴维南等效电阻。

所谓等效是指用戴维南等效电路把有源一端口网络置换后，对有源端口（1-1’）以外的电路的求解是没有任何影响的，也就是说对端口1-1’以外的电路而言，电流和电压仍然等于置换前的值。

外电路可以是不同的。

2.诺顿定理是戴维南定理的对偶形式。

指出对于外部电路，包含独立电源、线性电阻和受控源的端口可以被电流源和电导的并联组合所取代。

电流源的电流等于端口的短路电流ISC，该端口的所有独立电源设置为零后，电导等于输入电导GEQ=L/req，如图2.3-1所示。

3、戴维南一诺顿定理的等效电路是对外部特性而言的，也就是说不管是时变的还是定常的，只要含源网络内部除独立的电源外都是线性元件，上述等值电路都是正确的。

4.戴维南等效电路参数的测量方法。

开路电压UOC的测量相对简单，可直接用电压表或补偿法测量；对于戴维南等效电阻req的获取，可采用以下方法：当网络包含电源时，应使用开路电压和短路电流法，但这种方法不能用于不允许外部电路直接短路的网络（例如，当网络的内部元件可能因短路电流过大而损坏时）；当网络不含电源时，采用伏安法、半电流法、半电压法、直接测量法等。

5、叠加定理（1）叠加定理是线性电路的一个重要定理，是分析线性电路的基础。

电路定理一、是非题1.叠加定理仅适用于线性电路，而不适用于非线性电路。

2.替代定理只适用于线性电路。

3.如果直流电路中含有一个非线性电阻元件，那么其余由线性元件组成的二端网络仍可用戴维南定理作等效变换。

4.将叠加定理应用于含受控源的电路时，当每一个独立源单独作用时，都需将受控源置零。

5.测得下图所示含源二端网络的开路电压U oc=1V，若a、b端接一个1k的电阻，则流过电阻的电流一定为1mA。

6.工作在匹配状态下的负载可获得最大功率，显然这时电路的效率最高。

7.某一含源二端网络N与固定负载电阻R L相连，现要求N向R L提供最大功率，则该网络N的内阻R S应满足的条件是R S=0。

答案部分1.答案(+)2.答案()3.答案(+)4.答案()5.答案()6.答案()7.答案(+)二、单项选择题1.图示电路中，B、C间短路电流的方向为(A)短路电流为零(B)由C到B(C)不好判定(D)由B到C2.图示电路中的U ab为(A)40V(B)60V(C)40V(D)60V3.电压源与电阻串联电路短路时电流为2A，功率损耗为400W。

则此电路的最大输出功率为 (A)100W (B)200W (C)400W (D)不能确定4.图示电路中的I为____。

(A)5A (B) 3.33A (C)2.5A (D)0A5.如左下图所示电路中U ab等于(A)50V (B)25V (C)0V (D)256.右上图示电路中，为使负载电阻R L获得最大功率，电阻R0应满足的条件是(A)R0=R L (B)R0=(C)R0=0(D)7.图示电路中，I S=0时，I=2A。

则当I S=8A时，I为(A)4A (B)6A (C)8A (D)8.4A8.图示网络的戴维南等效电路为9.左下图示有源二端电阻网络A外接电阻R为12时，I=2A；R短路时，I=5A。

则当R为24时I为(A)4A (B)2.5A (C)1.25A (D)1A答案部分1.(D)2.(D)3.(A)4.(D)5.(A)6.(B)7.(C)8.(D)9.(C)三、填空题1.某二端网络端口电压u与i的关系为u=8i2。

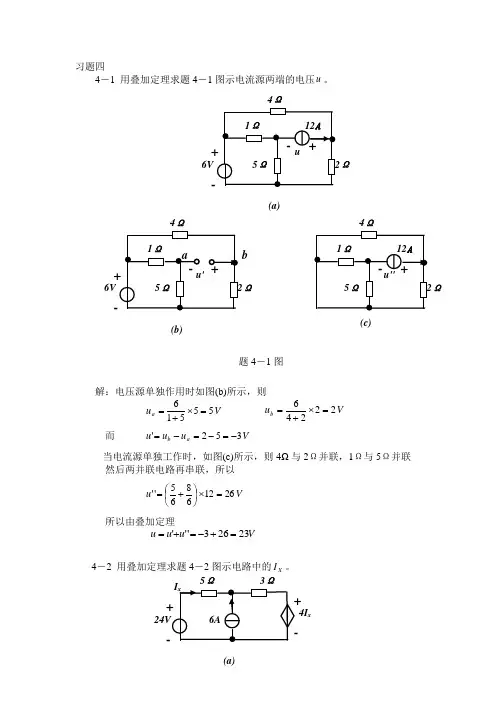
习题四4－1 用叠加定理求题4－1图示电流源两端的电压u 。

解：电压源单独作用时如图(b)所示，则V u a 55516=⨯+= V u b 22246=⨯+=而 V u u u a b 352'-=-=-=当电流源单独工作时，如图(c)所示，则4Ω与2Ω并联，1Ω与5Ω并联然后两并联电路再串联，所以V u 26126865''=⨯⎪⎭⎫⎝⎛+=所以由叠加定理V u u u 23263'''=+-=+=4－2 用叠加定理求题4－2图示电路中的X I 。

题4－1图 6V 4Ω Ω (b)b (c) 4Ω Ω5Ω 3Ω (a)4I x6V 4Ω Ω (a)解：电压源单独作用时的电路如图(b) 所示，则()24435''=++x x I I 解得 A I x 2'=电流源单独作用时的电路如图(c)所示，图中虚线为网孔电流，则 ()0''4''63''5=+++x x x I I I 解得 A I x 5.1''-= 所以 A I I I x x x 5.05.12'''=-=+=4－3 用叠加定理求题4－3图示电路中的独立电压源和独立电流源发出的功率。

5Ω 3Ω '(b) 4I 'x 4I ''x5Ω 3Ω I ''x(c) 题4－2图 题4－3图 2A 4Ω (a) 2V2A 4Ω 2i'(b) + - i''14Ω (c) u''1 2V解：电流源单独作用时的电路如图(b) 所示，则A i 2'1= 0'=i则 V i i u 824''1'1=-=电压源单独作用时的电路如图(b) 所示，则A i 5.042''1-=-= A i i 5.0''1''=-=则 V i u 122''''1=-=所以由叠加定理 A i i i 5.15.02''1'11=-=+=V u u u 918''1'11=+=+=可得电压源和电流源的功率分别为W i P V 3212-=-= W u P A 18212==4－4 题4－4图示电路中，R N 为电阻网络，由两个电流源供电。

习题和习题答案第 4 章必做习题习题 4-1 电路如图题 4.1 所示，求 6 Ω电阻吸收的功率。

习题 4-2 电路如图题 4.2 所示，试用叠加定理求电流 I 。

习题 4-3 电路如图题 4.3 所示，用戴维南定理计算 5 Ω电阻吸收的功率。

习题 4-4 电路如图题 4.4 所示，求 a 、 b 两端的诺顿等效电路。

习题 4-5 电路如图题 4.5 所示，用戴维南定理求电流 I 。

习题 4-6 电路如图题 4.6 所示，试问电阻 R 为何值时获得最大功率？并求最大功率。

第 4 章选做习题选做题 4-1 电路如图题 4.1 所示， N 是线性电阻网络，三个独立源 uS1 、uS2 和 iS 同时对 N 激励时，测得电流 i= 12A ；若将电压源 uS2 短路时，测得电流 i= 20A ；若将电压源 uS1 短路时，测得电流 i= － 5A 。

试问：将电流源 iS 和电压源 uS2 同时反向，而电压源 uS1 保持不变，电流 i 为多少？选做题 4-2 图题 4.2 所示电路中，已知 Uab=0 ，试用替代定理求电阻 R 。

选做题 4-3 电路如图题 4.3 所示，求 a 、 b 两端的戴维南等效电路。

选做题 4-4 图题 4.4 所示电路中， RL 可调，问 RL 为何值时获得最大功率？最大功率是多少？选做题 4-5 图题 4.17 所示电路中， Ns 是线性含源二端网络，电流表 A 和电压表 V 均是理想的，当开关 S 处于位置 1 时，电流表的读数为 2A ，当开关S 处于位置 2 时，电压表的读数为 4V ，求开关 S 处于位置 3 时， 5 Ω电阻吸收的功率。

选做题 4-6 求图题 4.6 所示电路中，电阻 R 获得最大功率时的电流 I 。

第 4 章必做习题精解习题 4-1解：为了求6 Ω电阻吸收的功率，就要先求出流过 6 Ω电阻的电流。

下面，用叠加定理计算电流 I 。

图题 4.1 电路中有两个独立源共同激励。

戴维南定理例题及答案1、解：将电阻R从电路中断开，如上左图。

显然，3Ω电阻和右侧的1A电流源变化为串联关系，所以3Ω电阻电流为1A。

对于节点n，KCL得到2Ω电阻电流：1+1=2（A）。

Uoc=Uab=Uan+Unb=1×3+2×2=7（V）。

将电压源短路、电流源开路，如上右图。

Req=Rab=3+2=5（Ω）。

最大功率传输定理：当R=Req=5Ω时，R获得最大功率，PLmax=Uoc²/（4R）=7²/（4×5）=2.45（W）。

解：原电路叠加定理：1、电压源作用时，电流源开路。

左上图。

电路电阻：R3+（R1+R2）∥R4=R+（R+R）∥2R=2R。

回路电流：I=（12-4）/2R=4/R，所以：U'=R×4/R=4（V）。

2、叠加定理的到：U"=U-U'=6-4=2（V）。

3、电流源单独激励，电压源短路，上中图，等效为上右图。

R1电压也为2V，则其电流为2/R，R4电流为1/R，KCL得到R2的电流为：2 /R+1/R=3/R，R2的电压为：R×3/R=3（V）。

R3两端电压：3+2=5V，电流为：5/R；Is=5/R+3/R=8/R。

电流源改变方向后的叠加：1、电压源作用时，响应不变：U'=4V。

2、电流源作用时，如右下图。

电流源外部总电阻：R3∥（R2+R1∥R4）=R∥（R +R∥2R）=5R/8。

端电压：（5R/8）×Is=（5R/8）×8/R=5（V），注意此时为下正上负。

并联支路的电流（即R2的电流）：5/（R+R∥2R）=3/R，方向为从下向上。

所以：U"=-（3/R）×（R∥2R）=-2（V）。

实际上，这一步不用这么复杂的计算；包括原电路的Is（上面的步骤3、）也不用计算。

因为根据线性电路激励与相应的性质关系，直接可得到：Is反向后，新的U"等于原来U"的相反数。

叠加定理习题1、电路如图所示，用叠加定理求电压U 。

2、 在图中，（1）当将开关S 和在a 点时，求123I I I 、和；（2）当将开关合在b 点时，利用（1）的结果，用叠加定理求支路电流123I I I 、和3、在图中，已知当S U =16V 时，ab U =8V ,求S U =0 时的ab U 。

4、在图所示电路中，已知0N 为一无源网络，当S U =2V 、S I =2A 时0U =5V;求S U =5V 、S I =5A 时的0U 。

5、在图2-33所示电路中，已知0N 为一无源网络，当S U =2V 、S I =3A 时0U =10V; 当S U =3V 、S I =2A 时0U =10V ，求S U =10V 、S I =10A 时的0U 。

弥尔曼定理习题1、求如图所示电路中的电流i。

2、求如图电路中A点的电位。

3、求图所示电路中的各支路电流，并计算2 电阻吸收的功率。

A6Ω8A 12V3Ω2Ω6V6ΩB+-+-I1I2I34、求如图所示电路中的支路电流I1、I2、I3。

5、如图所示电路中，E1=12V，E2=30V，I S=2A，R1=3Ω，R2=6Ω，求I1、I2。

6、电路如图所示，求各支路电流。

7、如图所示电路，求出各支路电流。

网孔电流法习题1、图示电路，已知E1 = 42 V，E2 = 21 V，R1 = 12 Ω，R2 = 3 Ω，R3 = 6 Ω，求各支路电流I1、I2、I3 。

2、求解电路中各条支路电流3、试用网孔电流法求如图所示电路中的支路电流I1、I2、I3。

4、如图所示电路中，U S=10V，I S=2A，R1=10Ω，R2=50Ω，R3=2Ω，R4=8Ω，用网孔电流法求I1、I2、I3。

5、如图所示电路，求出各支路电流。

6、电路如图所示，求各支路电流。

戴维宁定理习题1、在图所示的电路中，分别用戴维宁定理求电流LI。

2、电路如图所示，（1）用戴维宁定理求电阻RL 中的电流IL；（2）若RL为可变电阻，求R L 获得的最大功率及此时的RL值。

答案：I S1发出功率52W ，I S2发出功率电路原理学习指导与习题集：叠加定理-戴维南定理
4-10 题图4-10所示电路中，已知电流源I s1=2A ，I s2=3A ，当3A 的电流源断开时，2A 的电流源输出功率为28W ，这时U 2=8V 。

当2 A 的电流源断开时，3A 的电流源输出功率为54W ，这时U 1=12V 。

求两个电流源同时作用时，每个电流源的输出功率。

78W
4-24 题图4-24所示电路中，已知U S1=24V ，U S2=18V ，R 1=2Ω，R 2=1Ω，R 3=3Ω。

试计算：(1) U S3=15V 时，R 3中的电流；
(2) R 3为多大时可获得最大功率，最大功率值是多少？(3) 欲使R 3中的电流为零，U S3应为多少？
答案：（1）i = 3A （2）30.667R =Ω时可获得最大功率，P max ＝45.4W （3）U S3 = 4V 4-36 题图4-37所示电路中所示网络A 含由独立电压源、电流源及线性电阻。

题图(a)中测得电压U ab =10V ；图(b)中测得U a 'b ' =4V 。

求图(c)中得电压U a ''b ''。

答案：U a ''b ''=6.67V
(c)
Ω
(b)题图4-37
(a)
I S1
题图4-10I S2
R U S1
R S2题图4-24。

v1.0 可编辑可修改第四章电路定理重点：1、叠加定理2、戴维南定理和诺顿定理难点：1、熟练地运用叠加定理、戴维南定理和诺顿定理分析计算电路。

2、掌握特勒根定理和互易定理，理解这两个定理在路分析中的意义。

4-1 叠加定理网络图论与矩阵论、计算方法等构成电路的计算机辅助分析的基础。

其中网络图论主要讨论电路分析中的拓扑规律性，从而便于电路方程的列写。

几个概念1．线性电路——Linear circuit由线性元件和独立源组成的电路称为线性电路。

2．激励与响应——excitation and response在电路中，独立源为电路的输入，对电路起着“激励”的作用，而其他元件的电压与电流只是激励引起的“响应”。

激励e响应r系统3．齐次性和可加性——homogeneity property and additivity property“齐次性”又称“比例性”，即激励增大K倍，响应也增大K倍；“可加性”意为激励的和产生的响应等于激励分别产生的响应的和。

“线性”的含义即包含了齐次性和可加性。

齐次性：可加性：叠加定理1．定理内容在线性电阻电路中，任一支路电流（电压）都是电路中各个独立电源单独作用时在该支路产生的电流（电压）之叠加。

此处的“线性电阻电路”，可以包含线性电阻、独立源和线性受控源等元件。

2．定理的应用方法将电路中的各个独立源分别单独列出，此时其他的电源置零——独立电压源用短路线代替，独立电流源用开路代替——分别求取出各独立源单独作用时产生的电流或电压。

计算时，电路中的电阻、受控源元件及其联接结构不变。

关于定理的说明1．只适用于线性电路2．进行叠加时，除去独立源外的所有元件，包含独立源的内阻都不能改变。

3．叠加时应该注意参考方向与叠加时的符号 4．功率的计算不能使用叠加定理例题1． 已知：电路如图所示– 6V +4– 6V +求：X U 及两个独立源和受控源分别产生的功率。

解：根据叠加定理，电路中电压源和电流源分别作用时的电路如图（b ）、（c ）所示。

第4章电路定理4-1XX 简单题4-2XX 叠加定理4-3XX 戴维宁定理4-201、试用叠加定理计算下图所示电路中US2=2V时，电压U4的大小。

若US1的大小不变，要使U4=0，则US2应等于多少？答案U4=-0.4V, Us2=1.2V4-202、电路如图所示。

（1）用叠加定理求各支路电流；（2）求电压源发出的功率。

答案I1=-50mA, I2=15mA, I3=60mA (2)电压源发出的功率为：P=25I1=-1.25W 4-204、4-205、求题3-22图示电路的电压U 和电流I 。

+-2I 110V+ -3A -+ U 4Ω 6Ω9Ω I 1题3-22图I例4－4 用叠加定理求图4－5(a)电路中电压u。

图4－5解：画出独立电压源u S 和独立电流源i S 单独作用的电路，如图(b)和(c)所示。

由此分别求得u’和u”,然后根据叠加定理将u’和u”相加得到电压u4-206、例4－1 利用叠加定理求图（a ）所示电路中的电压U 。

（a ） (b) (c)解：首先画出分电路图如图(b)、(c)所示。

当12V 电压源作用时，应用分压原理有：V 43912)1(-=⨯-=U 当3A 电流源作用时，应用分流公式得：V 633636)2(=⨯+⨯=U 则所求电压：V 264=+-=US 4242"S 424' i R R R R u u R R R u +=+=)(S 2S 424"'i R u R R R u u u ++=+=4-207、例4－2利用叠加定理求图（a ）所示电路中的电压u 和电流i 。

（a ） (b) (c)解：首先画出分电路图如图(b)、(c)所示。

当 10V 电源作用时：)12/()210()1()1(+-=i i解得：A i2)1(=，V i i i u 6321)1()1()1()1(==+⨯=当5A 电源作用时，由左边回路的KVL ：02)5(12)2()2()2(=++⨯+i i i解得：A i1)2(-=，V i u 22)2()2(=-=所以： V u u u 8)2()1(=+=A i ii 1)2()1(=+=注意：受控源始终保留在分电路中。