方程求根计算方法及实验

一、实验目的通过本次综合实验，掌握数值分析中常用的插值方法、方程求根方法以及数值积分方法，了解这些方法在实际问题中的应用，提高数值计算能力。

二、实验内容1. 插值方法（1）拉格朗日插值法：利用已知数据点构造多项式，以逼近未知函数。

（2）牛顿插值法：在拉格朗日插值法的基础上，通过增加基函数，提高逼近精度。

2. 方程求根方法（1）二分法：适用于函数在区间内有正负值的情况，通过不断缩小区间来逼近根。

（2）Newton法：利用函数的导数信息，通过迭代逼近根。

（3）不动点迭代法：将方程转化为不动点问题，通过迭代逼近根。

3. 数值积分方法（1）矩形法：将积分区间等分，近似计算函数值的和。

（2）梯形法：将积分区间分成若干等分，用梯形面积近似计算积分。

（3）辛普森法：在梯形法的基础上，将每个小区间再等分，提高逼近精度。

三、实验步骤1. 拉格朗日插值法（1）输入已知数据点，构造拉格朗日插值多项式。

（2）计算插值多项式在未知点的函数值。

2. 牛顿插值法（1）输入已知数据点，构造牛顿插值多项式。

（2）计算插值多项式在未知点的函数值。

3. 方程求根方法（1）输入方程和初始值。

（2）选择求解方法（二分法、Newton法、不动点迭代法）。

（3）迭代计算，直到满足精度要求。

4. 数值积分方法（1）输入被积函数和积分区间。

（2）选择积分方法（矩形法、梯形法、辛普森法）。

（3）计算积分值。

四、实验结果与分析1. 插值方法（1）拉格朗日插值法：通过构造多项式，可以较好地逼近已知数据点。

（2）牛顿插值法：在拉格朗日插值法的基础上，增加了基函数，提高了逼近精度。

2. 方程求根方法（1）二分法：适用于函数在区间内有正负值的情况，计算简单，但收敛速度较慢。

（2）Newton法：利用函数的导数信息，收敛速度较快，但可能存在数值不稳定问题。

（3）不动点迭代法：将方程转化为不动点问题，收敛速度较快，但可能存在初始值选择不当的问题。

3. 数值积分方法（1）矩形法：计算简单，但精度较低。

数值计算⽅法⽅程求根数值计算⽅法实验报告实验内容：⽅程求根实验室：专业班级：学号：姓名：2.⽤MATBAB软件，⽤⼆分法求⽅程f（x）=x^3+4*x^2-10=0在区间[1,2]内根的近似值，为使误差不超过10^-5时所需要的⼆分次数。

function bisection_time(tolerance)a=1;b=2;k=0;while(abs(b-a)>tolerance)c=(a+b)/2;fa=a^3+4*a^2-10;fb=b^3+4*b^2-10;fc=c^3+4*c^2-10;if((fa==0)|(fc==0))disp(k);elseif(fa*fc<0)b=c;k=k+1;elseif(fc*fb<0)a=c;k=k+1;elseif(fb==0)disp(k);endendsoluntion=(a+b)/2;disp(soluntion);disp(k);运⾏结果1.36523176.取x0=1.5，⽤⽜顿迭代法求f（x）=x^3+4*x^2-10=0的跟的近似值function new(tolerance)x0=1.5;k=0;a=x0^3+4*x0^2-10;b=3*x0^2+8*x0;x1=x0-a/b;while(abs(x0-x1)>tolerance)x0=x1;k=k+1;a=x0^3+4*x0^2-10;b=3*x0^2+8*x0;x1=x0-a/b;enddisp(x1);disp(k);运⾏结果1.3652338.弦割法求⽅程f（x）=x^3-3*x^2-x+9=0在区间[-2，-1]内的⼀个实根近似值Xk，使|f(x) |<=10^-5. function xuange(k)x0=-2;x1=-1;t=0;a=x1^3-3*x1^2-x1+9;b=x0^3-3*x0^2-x0+9;x2=x1-a*(x1-x0)/(a-b);while(abs(x1-x0)>k)x0=x1;x1=x2;a=x1^3-3*x1^2-x1+9;b=x0^3-3*x0^2-x0+9;x2=x1-a*(x1-x0)/(a-b);t=t+1;enddisp(x1);disp(t)运⾏结果-1.52510269.⽤艾特肯算法求⽅程f （x ）=x^3+4*x^2+10=0在区间[1,2]内的根的近似值（取X0=1.5，g （x ）=410x ，精确到|Xk+1-Xk|<=10^-5，并与第2,3,6题的相应结果进⾏⽐较。

《数值分析》实验报告实验一方程求根一、实验目的:掌握二分法、Newton法、不动点迭代法、弦截法求方程的根的各种计算方法、并实施程序调试和运行，学习应用这些算法于实际问题。

二、实验内容:二分法、Newton法、不动点迭代法、弦截法求方程的根、程序的调试和运行，给出实例的计算结果。

观察初值对收敛性的影响。

三、实验步骤：①、二分法：定义：对于区间[a，b]上连续不断且f（a）·f（b）<0的函数y=f（x），通过不断地把函数f（x）的零点所在的区间一分为二，使区间的两个端点逐步逼近零点，进而得到零点近似值的方法叫二分法。

实现方法：首先我们设一方程400*(x^4)-300*(x^3)+200*(x^2)-10*x-1=0，并求其在区间[0.1,1]上的根，误差限为e=10^-4。

PS：本方法应用的软件为matlab。

disp('二分法')a=0.1;b=1;tol=0.0001;n0=100;fa=400*(a.^4)-300*(a.^3)+200*(a.^2)-10*a-1;for i=1:n0 p=(a+b)/2;fp=400*(p.^4)-300*(p.^3)+200*(p.^2)-10*p-1;if fp==0||(abs((b-a)/2)<tol)disp('用二分法求得方程的根p=')disp(p)disp('二分迭代次数为：')disp(i)break;end;if fa*fp>0 a=p;else b=p;end;end;if i==n0&&~(fp==0||(abs((b-a)/2)<tol)) disp(n0) disp('次二分迭代后没有求出方程的根')end;程序调试：运行结果：用二分法求得方程的根p=0.1108二分迭代次数为：14②Newton法定义：取定初值x0，找到函数对应的点，然后通过该点作函数切线，交x轴，得到新的横坐标值，然后找函数对应的点，做切线，得到新的横坐标值,重复上述步骤，多次迭代，直到收敛到需要的精度。

实验一 方程求根一、实验目的用不同方法求任意实函数方程f （x ）=0在自变量区间[a ，b]内或某一点附近的实根，并比较方法的优劣性。

二、实验方法 （1）二分法对方程f （x ）=0在[a ，b]内求根。

将所给区间二等分，在二分点x=(b-a)/2处判断是否f （x ）=0。

若是，则有根x=(b-a)/2；否则继续判断是否f(a)·f(b)<0,若是，则令b=x ，否则令a=x 。

重复此过程，直至求出方程f(x)=0在[a ，b]内的近似根为止。

（2）迭代法将方程f （x ）=0等价变换为x=φ（x ）的形式并建立相应的近似根为止。

（3）牛顿法设已知方程f （x ）=0的一个近似根x 0,则函数f （x ）在点x 0附近可用一阶泰勒多项式p 1（x ）=f （x 0）+f ’（x 0）（x-x 0）来近似，因此方程f （x ）=0可近似表示为f （x 0）+f ’（x 0）（x-x 0）=0。

设f ’（x 0）≠0，则 x=x 0-f （x 0）/’f （x 0）取x 作为原方程新的近似根x 1，然后再将x 1作为x 0代入上式。

迭代公式为 x k+1=x k -f （x k ）/f ’（x k ）三、实验内容1）在区间[0,1]内用二分法求方程e x +10x-2=0的近似根，要求误差不超过0.5×10-3。

2）取初值x0=0，用迭代公式x k+1=（2-e x k ）/10,(k=0,1,2,…)求方程e x + 10x-2=0的近似根，要求误差不超过0.5×10-3。

3）取初值x 0=0用牛顿迭代法求方程e x + 10x-2=0的近似根，要求误差不超过0.5×10-3。

四、实验程序 （1）二分法（2）迭代法（3）牛顿法五、实验结果（仅供参考）（1）x11=0.09033 （2）x5=0.09052 （3）x2=0.09052六、结果分析由上面的对二分法、迭代法、牛顿法三种方法的三次实验结果，我们可以得出这样的结论：二分法要循环k=10次，迭代法要迭代k=4次，牛顿法要迭代k=2次才能达到精度为0.5×10-3的要求，而且方程e x+10x-2=0的精确解经计算，为0.0905250,由此可知，牛顿法和迭代法的精确度要优越于二分法。

五. 讨论分析当初始值选取离零点较远时将导致算法无法使用，例如第三题，将初始值改为2就无法计算出结果了，显示如下例如求020sin 35=-+-x x e x 的根，其中控制精度1010-=eps ，最大迭代次数40=M ,在steffensen 加速迭代方法的程序中，我们只需改动：it_max=40; ep=1e-10， 其余不变 。

利用以上程序，我们只需输入：phi=inline('exp(5*x)-sin(x)+(x)^3-20');[x_star,index,it]=steffensen(phi,0.5)可得：x_star = 0.637246094753909index = 0it = 41观察上述结果，index = 0，it = 41表明迭代失败，所以使用以上方法估计的时候，应该尽量估计出解的范围，偏离不应过大，距离增加迭代次数增加，也有可能迭代失败六. 改进实验建议根据上述分析，我认为，应该先对函数作一个简图，方便知道解的大概位置，然后我们才将这个大概值代入Newton 法或者Steffensen 中进行求解。

当然，我们可以用其他数学软件实现Newton 迭代法，我们可以用z-z 超级画板，其操作流程为：牛顿迭代法的公式是：x n+1=x n-f(x n)/f'(x n)。

下面我们就用牛顿迭代法设计程序求方程f(x)=ln(x)+2*x-6的近似解。

（一）观察方程f(x)=0的零点位置（1）显示坐标系的坐标刻度。

（2）作出函数y=ln(x)+2*x-6的图像，如下图所示：可以观察到方程的根在区间[2，3]上，我们可以设定近似解的初始值为2。

（二）设计求方程近似解的程序（1）在程序工作区中输入：f(x){ln(x)+2*x-6;}执行后，返回结果为：>> f(x) #这表示在计算机已经完成了函数f(x)的定义。

（2）定义f(x)的导函数g(x)，在程序工作区中输入：Diff(f(x),x);执行后，返回结果为：>> 2+1/x #得到了f(x)的导函数。

实验四 方程求根实验一. 实验目的（1）深入理解方程求根的迭代法的设计思想，学会利用校正技术和松弛技术解决某些实际的非线性方程问题，比较这些方法解题的不同之处。

（2）熟悉Matlab 编程环境，利用Matlab 解决具体的方程求根问题。

二. 实验要求用Matlab 软件实现根的二分搜索、迭代法、Newton 法、快速弦截法和弦截法，并用实例在计算机上计算。

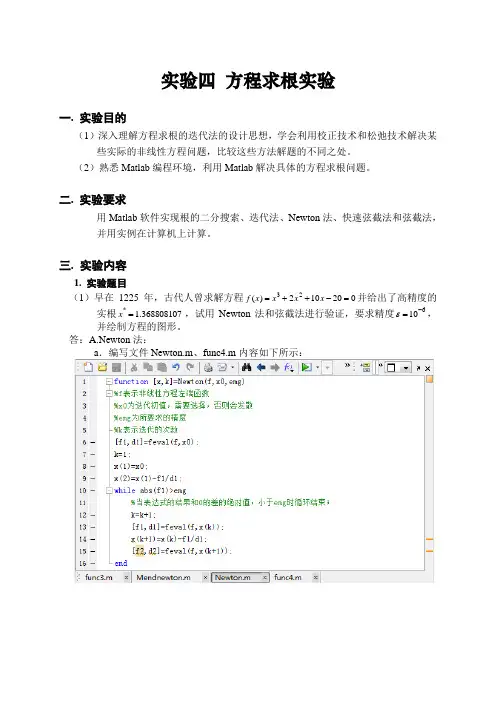
三. 实验内容1. 实验题目（1）早在1225年，古代人曾求解方程020102)(23=-++=x x x x f 并给出了高精度的实根368808107.1*=x ，试用Newton 法和弦截法进行验证，要求精度610-=ε，并绘制方程的图形。

答：A.Newton 法：a ．编写文件Newton.m 、func4.m 内容如下所示：b.运行，如下所示A为矩阵，由上面可知，对于初值为5，运行7次即可得到所需的精度，验证结果为古人给出的解释正确的；c.作图，编写下面的文件photo1.m.然后运行即可：注意下面中的x矩阵即为刚才计算出来的x系列，k为迭代的次数：a．编写文件Chord.m内容如下所示：b．运行结果如下所示：由上表可知，在精度为10^-6时有7位有效数字，古人的结果还是正确的c．作图，在上面运行后，即运行newton法时写的photo1.m文件即可出现图像：可以看到图中两条曲线基本重合； （2）取5.00=x ，用迭代法求方程x e x -=的根，然后用Aitken 方法加速，要求精度为结果有4为有效数字。

答：a. 编写文件func7.m 和Aiken.m ，内容如下所示：b ．运行：具有四位有效数字 （3）用快速弦截法求解方程01)(=-=x xe x f ，要求精度为610-=ε，取6.05.010==x x ，作为开始值，并绘制1)(-=x xe x f 的图形。

答：对照可知，书本后面的程序已经正确，运行即可：下面为快速弦截法的主程序文件：函数文件如下：运行如下：作图，编写下面的文件：运行该文件就可以y=x*exp(x)-1函数和插值函数的图：可以看到两条直线基本重合在一起了，扩大图片可以看到两条直线是不重合的：2. 设计思想要求针对上述题目，详细分析每种算法的设计思想。

解方程求根公式法解方程求根公式法是数学中一种重要的方法，它可以用来求解各种类型的方程，比如一元二次方程、三次方程、四次方程等等。

本文将详细介绍解方程求根公式法的原理、步骤和应用。

一、原理解方程求根公式法的原理是基于代数运算的基本定理和根的概念。

对于一个一元n次方程 a_n x^n + a_{n-1} x^{n-1} + ... + a_1 x + a_0 = 0，其中a_n ≠ 0，我们可以通过求解它的根来解方程。

如果该方程的根为 x_1，x_2，...，x_n，则有：a_n (x-x_1)(x-x_2)...(x-x_n) = a_n x^n - (a_n x^{n-1})(x_1 + x_2 + ... + x_n) + ... + (-1)^n a_0由代数运算基本定理可知，左边的乘积展开式中，x^n 的系数为1，且各项系数为整数。

因此，我们可以将该方程转化为a_n x^n - (a_n x^{n-1})(x_1 + x_2 + ... + x_n) + ... + (-1)^n a_0 = 0 的形式，然后通过求解根的和、积、差等运算，得到解方程的根。

二、步骤解方程求根公式法的步骤通常如下：1.将一元n次方程化为标准形式，即a_n x^n + a_{n-1} x^{n-1}+ ... + a_1 x + a_0 = 0。

2.根据方程的次数和系数，选择适当的求根公式。

例如，对于一元二次方程a x^2 + b x + c = 0，我们可以使用公式x = (-b ± √(b^2 - 4ac)) / 2a 来求解。

3.代入系数，按照公式计算根的值。

4.检查解的合法性，即检查解是否满足原方程。

5.如果有多个根，重复步骤3-4即可。

三、应用解方程求根公式法在实际应用中非常广泛，比如在物理、工程、金融等领域都有重要的应用。

以下是一些常见的例子：1.一元二次方程的求解。

例如，求解方程 x^2 + 2x - 3 = 0 的根。

求根公式的应用求根公式是解决二次方程的一种常用方法，它可以帮助我们求解形如ax^2+bx+c=0的方程，其中a、b、c是已知的实数常量且a≠0。

通过求根公式，我们可以方便地得到二次方程的根，进而解决各种实际问题。

本文将介绍求根公式的应用以及如何使用当中的步骤。

一、求根公式的基本形式在介绍求根公式的应用之前，我们先来回顾一下求根公式的基本形式：对于二次方程ax^2+bx+c=0，它的根可以通过求根公式得到：x = (-b ± √(b^2-4ac))/2a其中，±表示两个解，即我们可以得到两个根x1和x2。

根据求根公式，我们可以知道二次方程的根与方程的系数a、b、c有关。

二、求根公式的应用举例接下来，我们将通过几个具体的例子来说明求根公式的应用。

例一：已知二次方程2x^2+5x-3=0，求方程的根。

根据求根公式，我们可以将方程的系数代入公式中，得到：x = (-(5) ± √((5)^2-4(2)(-3)))/2(2)化简后可得：x = (-5 ± √(25+24))/4x = (-5 ± √49)/4x1 = (-5 + 7)/4 = 2/4 = 1/2x2 = (-5 - 7)/4 = -12/4 = -3所以，方程2x^2+5x-3=0的根为x1=1/2和x2=-3。

例二：一个矩形的长比宽多9米，其面积为60平方米，求矩形的长和宽。

假设矩形的宽为x，则矩形的长为x+9。

根据矩形的面积公式，我们可以写出方程：(x+9)x=60化简后得到二次方程：x^2+9x-60=0使用求根公式，我们有：x = (-(9) ± √((9)^2-4(1)(-60)))/2(1)化简后可得：x = (-9 ± √(81+240))/2x = (-9 ± √321)/2这样，我们得到了矩形的宽的两个候选值。

为了满足实际问题的要求，我们只需要考虑正数值的宽度，所以我们选择：x = (-9 + √321)/2计算得到x ≈ 4.24由此可得矩形的宽度约为4.24米，代入矩形的长为x+9，即长约为13.24米。

实验一_方程求根的数值方法实验一方程求根的数值方法一、实验内容：1.求方程3310x x--=在02x=附近的根（根的准确值为）* 1.87938524x= ，要求计算结果准确到四位有效数字。

2.给出至少三种不同的数值方法，并写出相应的理论分析；3.编写程序，上机计算，求出数值结果，在实验报告中以表格形式列出；4.对数值实验结果进行分析，验证与前面理论分析是否一致。

二、实验报告格式1. 题目（手写）；2. 数值方法和相应的理论分析（手写）；3. 程序（打印）；4. 数值实验结果（打印）；5. 数值实验结果分析（手写）。

三、实验报告要求理论分析正确，程序运行无误。

实验报告条理清晰，手写部分字迹工整整洁。

不动点迭代法程序：function [r,n]=mulStablePoint(F,x0,eps)%非线性方程组：f%初始解：a%解的精度：eps%求得的一组解：r%迭代步数：nif nargin==2eps=1.0e-6;endx0 = transpose(x0);n=1;tol=1;while tol>epsr= subs(F,findsym(F),x0) %迭代公式tol=norm(r-x0); %norm 为矩阵的欧几里得范数n=n+1;x0=r;if(n>100000) %迭代步数控制disp('迭代步数太多可能不收敛');return;endend实验结果K Xk X*0 2.0000 1.879385241 1.9129 1.879385242 1.8888 1.879385243 1.8821 1.879385244 1.8801 1.879385245 1.8796 1.87938524牛顿法迭代程序：function [r,n]=mulNewton(F,x0,eps)if nargin==2eps=1.0e-4;endx0 = transpose(x0);Fx = subs(F,findsym(F),x0);var = findsym(F);dF = jacobian(F,var);dFx = subs(dF,findsym(dF),x0);r=x0-inv(dFx)*Fx;n=1;tol=1;while tol>epsx0=r;Fx = subs(F,findsym(F),x0);dFx = subs(dF,findsym(dF),x0);r=x0-inv(dFx)*Fx %核心迭代公式tol=norm(r-x0);n=n+1;if(n>100000)disp('迭代步数太多可能不收敛'); return;endend实验结果：K Xk X*0 2.0000 1.879385241 1.8795 1.879385242 1.8794 1.87938524弦截法代码：function root=ModifSecant(f,a,b,eps) format long;if(nargin==3)eps=1.0e-4;endf1=subs(sym(f),findsym(sym(f)),a);f2=subs(sym(f),findsym(sym(f)),b);if(f1==0)root=a;endif(f2==0)root=b;endif(f1*f2>0)disp('两端点函数值成绩大于0!’)return;elsetol = 1;r1 = a; %迭代初始值r2 = b; fv = subs(sym(f),findsym(sym(f)),a);while(tol>eps)f2=subs(sym(f),findsym(sym(f)),r2);root=r2-(r2-r1)*f2/(f2-fv)fr=subs(sym(f),findsym(sym(f)),root);if(f2*fr<0)tol=abs(root-r2);r1 = r2;r2 = root;fv = subs(sym(f),findsym(sym(f)),r1);elsetol=abs(root-r2);r2 = root;fv = 0.5*subs(sym(f),findsym(sym(f)),r1);endendendformat short;实验结果：K Xk X*0 2.0000 1.879385241 1.8724 1.879385242 1.8845 1.879385243 1.8793 1.879385244 1.8794 1.87938524。

《数值分析》实验报告一**: **学号: PB********实验一一、实验名称方程求根二、实验目的与要求：通过对二分法和牛顿法作编程练习和上机运算，进一步体会它们在方程求根中的不同特点；比较二者的计算速度和计算精度。

三、实验内容：通过对二分法和牛顿迭代法作编程练习和上机运算，进一步体会它们在方程求根中的不同特点 。

（一）二分法算法：给定区间[a,b]，并设f （a ）与f （b ）符号相反，取δ为根的容许误差，ε为值的容许误差。

（1）令c=(a+b)/2（2）如果(c-a)< δ或)(c f <ε，则输出c ，结束；否则执行（3）（3）如果f(a)f(c)<0，则令)()(,c f b f c b ←←；否则，则令)()(,c f a f c a ←←，重复（1），（2），（3）。

（二）牛顿迭代法：给定初值0x ，ε为根的容许误差，η为)(x f 的容许误差，N 为迭代次数的容许值。

（1）如果)(x f <η或迭代次数大于N ，则算法结束；否则执行（2）。

（2）计算)('/)(0001x f x f x x -=（3）若 < 或 < ，则输出 ，程序结束；否则执行（4）。

（4）令 = ，转向（1）。

四、实验题目与程序设计1、二分法3.1.1、用二分法求方程a. f(x)= x x tan 1--在区间[0，π/2]上的根,c. f(x)=6cos 22-++-x e x x 在区间[1，3]上的根。

源程序：3.1.1.a#include<stdio.h>#include<math.h>void main(){float a,b;double c,y,z;printf("plese input two number a and b:\n");scanf("%f%f",&a,&b);c=(a+b)/2;y=1/c-tan(c);printf("a=%f,b=%f,b-a=%f,c=%f,f(c)=%f\n",a,b,b-a,c,y);while(fabs(b-a)>0.00001|| fabs(y)>0.00001){z=1/a-tan(a);if(z*y<0)b=c;elsea=c;c=(a+b)/2;y=1/c-tan(c);printf("a=%f,b=%f,b-a=%f,c=%f,f(c)=%f\n",a,b,b-a,c,y);}x x 01-ε)(1x f ηx 1x 0x 1}输入0 1.5707563( /2~1.5705563)得到下表：由上表可以看出刚开始时f（c）取值幅度很大，但是经过一段历程之后，幅度变得平缓甚至基本接近与零，我们认为，x=0.8603是方程的根，结果与实际想要得到的值相当接近。

班级： 学号： 姓名： 成绩：实验2 非线性方程的数值解法实验1实验目的1）进一步熟练掌握求解非线性方程的牛顿迭代法和弦截法。

2）根据牛顿迭代法和弦截法的原理，编写程序求解非线性方程，提高编程解决问题的能力。

2 实验内容（1）用牛顿法和割线法求下列方程的根x^2-e^x=0;x*e^x-1=0;（23实验原理（1）牛顿迭代公式：1()/'()k k k k x x f x f x +=- 双点弦法公式：111()()()()k k k k k k k f x x x x x f x f x +--=--- （2）令2()f x x A =-，再用牛顿法求根。

4实验步骤1)根据牛顿迭代法，双点弦法的算法编写相应的求根函数；2)用牛顿迭代法和双点弦法分别对方程进行求解；5 程序设计牛顿迭代法x0=1.0;N=100;k=0;eps=5e-6;delta=1e-6;while(1)x1=x0-fc1(x0)/fc2(x0);k=k+1;if k>Ndisp('Newton method failed')breakendif(abs(x1-x0)<delta || abs(fc1(x1))<delta) break;endx0=x1;endfprintf('%f',x0)fprintf('%f',abs(fc1(x1)))双点弦法function cutline(x0,x1)N=100;k=0;delta=5e-8;while(1)(abs(x1-x0)>=delta)c=x1;x1=cutnext(x0,x1);x0=c;k=k+1;if k>Ndisp('Cutline method failed')break;endif(abs(x1-x0)<delta || abs(fc1(x1))<delta) break;endendfprintf('%10f\n',x1);function y=cutnext(a,b)y=b-fc(b)/(fc(b)-fc(a))*(b-a);1）原函数function fc1=fc1(x)fc1=x^2-exp(x);end导函数function fc2=fc2(x)fc2=2*x-exp(x);end2）原函数导函数3）原函数导函数6实验结果及分析注：牛顿迭代法由于设置delta=1e-6，所以算出的误差e<1.0*10^-6;割线法由于设置delta=5e-8，所以误差e<5.0*10^-8.7总结。

计算方法实验题目：班级：学号：姓名：目录计算方法实验 (1)1 实验目的 (3)2 实验步骤 (3)2.1环境配置： (3)2.2添加头文件 (3)2.3主要模块 (3)3 代码 (3)3.1主程序部分 (3)3.2多项式方程部分 (4)3.3核心算法部分 (7)3.4数据结构部分 (11)4运行结果 (16)4.1二分法运行结果 (16)4.2牛顿迭代法运行结果 (17)4.3割线法运行结果 (18)边界情况调试 (18)5总结 (19)输入输出.............................................................................. 错误！未定义书签。

二分法.................................................................................. 错误！未定义书签。

牛顿迭代法.......................................................................... 错误！未定义书签。

割线法.................................................................................. 错误！未定义书签。

6参考资料. (19)1 实验目的1.通过编程加深二分法、牛顿法和割线法求解多项式方程的理解2.观察上述三种方法的计算稳定性和求解精度并比较各种方法利弊2 实验步骤2.1环境配置：VS2013，C++控制台程序2.2添加头文件#include "stdio.h"#include "stdlib.h"#include "stdafx.h"2.3主要模块程序一共分成三层，最底层是数据结构部分，负责存储数据，第二层是交互部分，即多项式方程部分，负责输入输出获得数据，最上层是核心的算法部分，负责处理已获得的数据。

根式方程的求解思路与方法根式方程是指含有根号（√）或分数指数的方程。

在解决根式方程时，我们需要使用一些特定的求解思路与方法。

本文将会介绍一些常见的根式方程求解方法，并提供一些实例来帮助读者理解和掌握这些方法。

一、分离有理部分和无理部分的根式方程对于形如√(a + √b) = c 的根式方程，其中a、b、c为实数，我们可以通过以下步骤求解：1.假设(a + √b) 的值为 x^2，其中 x 为未知数。

2.根据假设的表达式(a + √b) = x^2，将 x 的平方进行化简，得到x^2 - a = √b。

3.整理方程，得到 x^2 - a - √b = 0。

4.接下来，我们需要将根号项和无根号项分开。

将无根号项移到方程的左边，根号项移到方程的右边。

x^2 - a = √b --> x^2 - a - √b = 0。

5.将方程两侧的等式平方，得到 (x^2 - a - √b)^2 = 0。

展开并化简得到 x^4 - 2ax^2 + (a^2 - b) = 0。

6.解这个二次方程 x^4 - 2ax^2 + (a^2 - b) = 0。

可以使用二次方程的求解公式或者其他方法求解。

例子：求解方程√(3 + √5) = x。

解答：我们将(3 + √5) 的值设为 x^2，即(3 + √5) = x^2。

化简得到 x^2 - 3 = √5，整理得到 x^2 - 3 - √5 = 0。

方程两侧平方，得到 (x^2 - 3 - √5)^2 = 0。

展开并化简得到 x^4 - 6x^2 + 4 - 6√5x^2 + 6√5 + 5 = 0。

合并同类项得到 x^4 - 6x^2 - 6√5x^2 + 6√5 + 9 = 0。

化简后得到 x^4 - (6 + 6√5)x^2 + 6√5 + 9 = 0。

这是一个关于 x 的二次方程，我们可以使用二次方程的求解公式来求得 x 的值。

二、分离分数指数与根号的根式方程对于形如∛(a + ∛b) = c 的根式方程，其中a、b、c为实数，我们可以通过以下步骤求解：1.假设 (a + ∛b) 的值为 x^3，其中 x 为未知数。