当前位置：文档之家 › 计算方法_4方程求根的迭代法

计算方法_4方程求根的迭代法

  • 格式：ppt
  • 大小：636.50 KB
  • 文档页数：67

下载文档原格式

  / 67

合集下载

计算方法4方程求根的迭代法

计算方法4方程求根的迭代法

计算方法4方程求根的迭代法四方程求根的迭代法是一种用于解决非线性方程的数值方法。

在计算方法中，非线性方程指的是形如f(x)=0的方程，其中f(x)包含x的非线性项。

在实际中，非线性方程的求解是非常常见的问题，因此有很多不同的迭代法可以用于解决这些问题。

以牛顿迭代法为例，它是一种基于线性近似的迭代方法。

该方法的基本思想是将非线性方程转化为线性方程，通过不断迭代来逼近方程的根。

具体而言，牛顿迭代法的步骤如下：1.选择初始估计值x0作为方程的根，并计算f(x0)的值。

2.计算f(x)的导数f'(x)，并计算方程的线性近似式x-x0=-f(x0)/f'(x0)。

3.计算下一个近似值x1，即x1=x0-f(x0)/f'(x0)。

4.判断，x1-x0，是否小于给定的收敛条件，如果是则停止迭代，否则转到步骤55.将x1作为新的近似值x0，转到步骤2牛顿迭代法具有快速收敛的特点，尤其适用于具有单根的方程。

然而，该方法也存在一些限制，如在计算f'(x)时需要知道方程的导数，当方程的导数不易计算时，该方法可能不适用。

除了牛顿迭代法，还有其他一些常用的四方程迭代方法，如割线法、弦截法等。

每种方法都有其特点和适用范围，选择合适的方法对于求根问题的解决至关重要。

总结起来，四方程求根的迭代法是一种用于解决非线性方程的数值方法。

牛顿迭代法是其中一种常用的方法，通过不断迭代来逼近方程的根。

根据方程的特点和计算条件，选择合适的迭代方法是解决求根问题的关键。

希望以上的介绍可以帮助您更好地理解和应用这一方法。

第4章 非线性方程求根的迭代法

第4章 非线性方程求根的迭代法
{ x k }。这种方法算为简单迭代法。
精选版课件ppt
18
若{ x k }收敛，即lkimxk x 称迭代法收敛，否则称迭代法发散
精选版课件ppt
19
迭代法的几何意义
x (x)yy(xx)交点的横坐标
y=x
x* x2
x1
x0
精选版课件ppt
20
例题
例 试用迭代法求方程
f(x)x3x10
在区间(1，2)内的实根。 解：由x3 x1 建立迭代关系
精选版课件ppt
30
例题
若取迭代函数 (x)x3 1 ， 因为|'(x)||3x2|3 x[1,2] 不满足压缩映像原理，故不能肯定 xn1 (xn) n0,1,....收敛到方程的根。
精选版课件ppt
31
简单迭代收敛情况的几何解释
精选版课件ppt
32
是否取到合适的初值，是否构造合适的 迭代格式，对于是否收敛是关键的。
x2 0.739085178
x3 0.739085133 x4 0.739085133
故取 x* x4 0.739085133
精选版课件ppt
48
例题
例 用Newton法计算 。 2
解： f(x)x2a0 其 中 a2
由 f (x) 2x及Newton迭代公式得
xn 1xnx2 n 2x n21 2(xnx 2 n) n0,1 ,......
迭代法及收敛性
考察方程 x(x)。不能直接求出它的
根，但如果给出根的某个猜测值 x 0， 代
入 x(x)中的右端得到x1 (x0) ，再以 x 1
为一个猜测值，代入x(x) 的右端
得 x2 (x1)

第四章 方程求根的迭代法

第四章 方程求根的迭代法

例5 已知方程 e − x = 0 在 x0 = 0.5 附近有一实根， 讨论迭代 x0 = 0.5 , xn+1 =ϕ(xn) = e−x 的敛散性.并计算结 ε = 10−5 果，取 .
−x
n
f (x) = e−x − x ，则 f (0.4) = 0.27 > 0, f (0.6) =−0.05 < 0 解：令
（c）
ϕ ′( x* ) < −1
（d）
定理2 定理 设函数 ϕ ( x ) 在[a,b]上具有连续的一阶导 上具有连续的一阶导 数, 且满足 对所有的x∈ （1）封闭性条件 ） 对所有的 ∈[a,b] 有 ) ] 推论: 若方程 x = ϕ ( x在区间 [ a, b内有根 x * ϕ ( x) ∈[a,b] 且 ϕ ′( x) ≥ 1 , ∀x ∈ [ a, b ] （2）压缩性条件 ） 存在 0 < L< 1 ,使所有的 使所有的 则迭代 xk +1 = ϕ ( xk ) , ∀x0 ∈ [ a, b ]均发散 x∈[a,b]有 ∈ 有
（1）一个迭代若是整体收敛的，则一 ）一个迭代若是整体收敛的， 定局部收敛；反之则不成立． 定局部收敛；反之则不成立． 对初值的要求比较高， （2）定理 对初值的要求比较高，一般 ）定理3对初值的要求比较高 用对分法找出较满意的初值，定理2对初 用对分法找出较满意的初值，定理 对初 值的要a ) xk +1 − a = 2 xk
x k +1 +
x k +1 − x k +1 +
2
( xk + a ) 2 a = 2 xk
a xk − =( a xk + a 2 ) a

数值分析10-方程求根的迭代法

数值分析10-方程求根的迭代法

压缩映像定理证明
(a) 由压缩映像定理可知，不动点 x* 存在且唯 一。
| xk − x* | = ϕ ( xk −1 ) − ϕ ( x*) =| ϕ '(ξ ) | ⋅ | xk −1 − x* |≤ L | xk −1 − x* |
| xk − x* | ≤ L | xk −1 − x* |≤ L2 | xk −2 − x* |≤
lim x n = x *
存在 等价于 几何 意义
ϕ ( x* ) = x*
* f ( x * ) = 0 x 为ϕ ( x )的不动点
⎧ y= x ⎨ ⎩ y = ϕ ( x)
转换例子
已知方程 x3-6x2+9x-2=0 在 [3,4] 内有一根，考虑迭代 例： (1) x = ϕ1(x) = x3-6x2+10x-2 ; (2) x = ϕ 2 ( x ) = ( x 3 + 9 x − 2 ) 6 ;
lim | xk − x* | = 0
k →∞
≤ Lk | x0 − x* |
压缩映像定理证明
(b) | xk +1 − x* | ≤ L | xk − x* |
| xk +1 − xk | =| ( xk +1 − x*) − ( xk − x*) |≥ xk − x * − xk +1 − x * ≥ (1 − L) xk − x *
ϕ ( x k ) − ϕ '( x k ) x k 1 − ϕ '( x k )
缺点：每次迭代需计算 ϕ '( x k )
埃特金算法
xk +1 − x* = ϕ '(ξ k )( xk − x*) xk + 2 − x* = ϕ '(ξ k +1 )( xk +1 − x*)

迭代法求方程根

迭代法求方程根

迭代法是求解方程根的一种重要方法，它是以某种特定的搜索路径，通过不断迭代更新搜索解的值，最终求得方程的根的一种方法。

迭代法的核心思想是迭代的方法，通俗理解就是不断重复，不断迭代，不断改变，最终找到满足条件的解。

迭代法求解方程根的步骤大致如下：
首先，选定迭代法求解方程的初始值和迭代步长，然后设定迭代次数，并进行初始化。

其次，开始对迭代解进行更新。

在这一步中，根据方程的性质，以及初始值和迭代步长，通过计算求出新的迭代解，然后将新的迭代解更新到原来的迭代解中。

接着，计算迭代解的误差，并根据误差的大小，来判断迭代解是否收敛。

如果迭代解收敛，则将其作为方程的根；如果迭代解不收敛，则重复前面的步骤，继续迭代，直到解收敛为止。

最后，根据迭代解的误差，判断迭代解是否准确，即判断迭代解是否符合方程的性质。

如果误差满足要求，则将迭代解作为方程的根；如果误差过大，则需要重新调整迭代步长，并重复迭代，直到误差满足要求为止。

总之，迭代法求解方程根是一种重要的方法，它可以解决复杂的方程，在求解方程根方面有很大的帮助。

它的基本思想是：以某一特定搜索路径，通过迭代不断改变搜索解，最终得到解。

方程求根的迭代法

方程求根的迭代法

方程求根的迭代法一、考核知识点：区间二分法，弦位法（单点弦法、双点弦法）、切线法、一般迭代法，收敛性。

二、考核要求：1．熟练掌握用区间二分法求方程近似根的方法。

2．熟练掌握用单点弦法、双点弦法求方程近似根的方法。

了解其收敛性。

3．熟练掌握用切线性求方程近似根的方法。

了解其收敛性。

4．掌握用一般迭代法求方程的方法近似根的方法。

了解其收敛性。

三、重、难点分析例1 证明计算)0(>a a 的切线法迭代公式为：,1,0),(211=+=+n x a x x nn n 并用它求2的近似值（求出1x 即可）解 （1）因计算a 等于求02=-a x 正根，a x x f -=2)(，x x f 2)(=' 代入切线法迭代公式得)(21221nn n n n n x a x x x x x +=-=+ ,1,0=n (2) 设2)(2-=x x f ，因,0121)1(2<-=-=f 025.1)5.1(2>-=f 所以 []5.1,12*∈=x在[]5.1,1上 02)(>='x x f 02)(>=''x f由 0)()(0≥''x f x f ，选5.10=x用上面导出的迭代公式计算得 4167.11217)2(21001≈=+=x x x例2用单点弦法求方程 0153=+-x x 的最小正根(计算出1x ) 解：由于0375.1)5.0(,01)0(<-=>=f f 则]5.0,0[*∈x 在[0，0.5]，,06)(,053)(2≥=''<-='x x f x x f 由,0)()(≥''x f c f 取5.0,00==x c 则单点弦法迭代公式 ,1,0)15(51),15(151032331=+--+=+--+---=+n x x x x x x x x x x x n n n n n n n n n n n 计算得 21.075.4375.15.01≈-=x 例3 用双点弦法，一般迭代法求0243=-+x x 的最小正根（求出2x 即可）。

方程求根的迭代法

方程求根的迭代法

§4.1 引 言绪论中讲到方程求根得二分法，但二分法收敛速度慢，有必要掌握新的方法。

§4.1.1迭代法的思想迭代法是一种逐次逼近法，使用某个固定公式（迭代公式）反复校正，逐步精确，直到满足精度。

迭代法求根分两步： 1） 猜测初值 2）迭代如求解初值问题00')(),,(y x y y x f y ==用梯形公式111[(,)(,)2n n n n n n h y y f x y f x y +++≈++ （1）看作关于1+n y 的函数方程，按欧拉公式提供猜测值),()0(1n n n n y x hf y y +=+，代入（1）得)],(),([2)0(11)1(1+++++=n n n n n n y x f y x f h y y若)1(1+n y 仍不满足要求，则将它代入（1）式，继续得到校正值)2(1+n y ，写成迭代公式)],(),([2)(11)1(1k n n n n n k n y x f y x f h y y ++++++= （2）一般地，为了求一元非线性方程0)(=x f 的根，可以先将其转换为如下的等价形式()x x ϕ= （3）式（3）中连续函数()x ϕ称为迭代函数，其右端含未知数，不能直接求解。

先用根的某个猜测值0x 代入（3），构造迭代公式：()k k x x ϕ=+1。

如果迭代值k x 有极限，则称迭代收敛，极限值k k x x ∞→=lim *就是方程（3）的根。

几何意义P127图4-1为使迭代法有效，必须保证它的收敛行，()x ϕ满足什么条件，才能保证收敛？以最简单的线性迭代()d kx x +=ϕ，可以看出收敛的充分必要条件()1'<=k x ϕ。

几何意义P127图4-2,3,4,5。

§4.1.3 压缩映像原理设*x 是方程()x x ϕ=的根，则由微分中值定理))(()()(*'*1*k k k x xx x x x-=-=-+εϕϕϕ，如果存在10<≤L ，使得],[b a x ∈有()k k x x L x x L x -≤-⇒≤+*1*'ϕ，则迭代误差0e L e kk ≤，由于10<≤L ，故0→k e ，即迭代收敛。

计算方法 4方程求根的迭代法

计算方法 4方程求根的迭代法

是所求方程(5―1)的根x。
我们把每次二分后的有根区间(ak,bk)的中点
1 xk ( ak bk ) 2
作为所求根x的近似值,这样获得一个近似根的序列
x0,x1,x2,…,xk,… 该序列必以根x为极限,即
lim xk x
k
1 x xk (bk ak ) bk 1 ak 1 2
表 5―1
§2
迭代法的基本思想是 : 首先将方程 (5―1) 改写成某 种等价形式,由等价形式构造相应的迭代公式,然后选取 方程的某个初始近似根x0,代入迭代公式反复校正根的 近似值,直到满足精度要求为止。迭代法是一种数值计 算中重要的逐次逼近方法。 例如,求方程 x3-x-1=0
在x=1.5附近的一个根(用六位有效数字计算)。
为下列等价形式 x=g(x) 然后按(5―7)构造迭代公式 (5―7)
xk 1 g ( xk ), k 0,1,2,
从给定的初始近似根 x0 出发 , 按迭代公式 (5―8) 可
以得到一个数列 x0,x1,x2,…,xk,… 若这个数列｛xk｝有极限,则迭代公式(5―8)是收敛 的。此时数列的极限
x y g(x ) g( y ) q x y
* * * * *
*
因为q＜1,所以上式矛盾,故必有
x y
亦即方程在(a,b)内有唯一的根。
再考虑迭代公式 x k+1=g(xk) , 由李普希茨条件 k=0,1,2,…
xk 1 x g ( xk ) g ( x ) qk x0 x
收敛。
②对于收敛的迭代过程,误差估计式(5―11)说明迭代值的 偏差｜xk-xk-1｜相当小,就能保证迭代误差｜x-xk｜足够小。

第4章方程求根的迭代法.ppt.ppt

第4章方程求根的迭代法.ppt.ppt

相应地可得到两个迭代公式
3 x x ( x ) k 1 1 k k 1 3 x ( x ) x 1 k 1 2 k k
如果取初始值 x 0 ＝1.5，用上述两个迭代公 式分别迭代，计算结果
3 （ 1 ） x 1 . 5 ， x , ( k 0 , 1 , 2 ,) . 0 k 1 x k1
仍平方收敛可将迭代法改为牛顿法不是平方收敛重根情形仍平方收敛用牛顿法得用上述三种方法求的二重根151458333333143660714314254976191514166666671414215686141421356215141176470614142114381414213562牛顿迭代法虽然具有收敛速度快的优点但每迭代一次都要计算导数比较复杂时不仅每次计算带来很多不便而且还可能十分麻烦如果用不计算导数的迭代方法往往只有线性收敛的速度
条件
* ( x) 1 2 a 5 1
1 1 2 a5 1
2 2 a5 0
所以

1 5
a0
(x ) 已知方程 x 在 a, b内有根 x *,且在 a, b 上满足 ,利用 ( x) 构造一个迭代函数 g ( x) (x )31
*
* * ( x ) x 当
* (x ) L 1
x x*
,使成立
( x ) ( x ) ( )( x x )
*
故有
( x ) x L x x x x
* * *
x

( x k 1 k) 对于任意的 x 都收敛 由定理1知 x 0
k 0 1 2 3 4 5 6 7
xk 1.5 1.35721 1.33086 1.32588 1.32494 1.32476 1.32473 1.32472

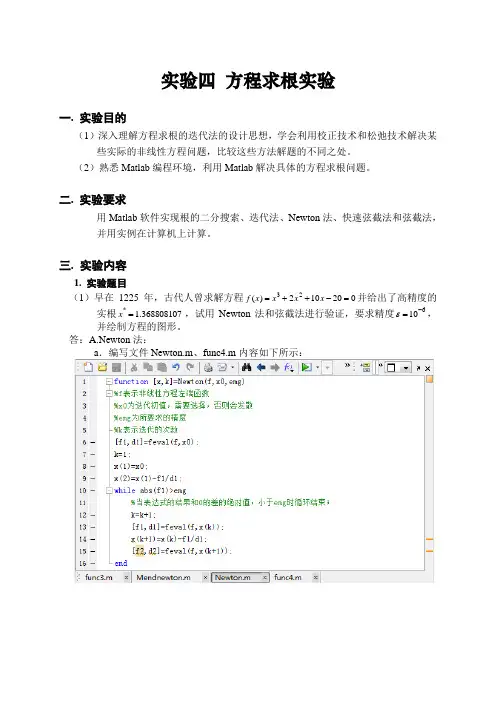
计算方法-方程求根实验

计算方法-方程求根实验

实验四 方程求根实验一. 实验目的（1）深入理解方程求根的迭代法的设计思想，学会利用校正技术和松弛技术解决某些实际的非线性方程问题，比较这些方法解题的不同之处。

（2）熟悉Matlab 编程环境，利用Matlab 解决具体的方程求根问题。

二. 实验要求用Matlab 软件实现根的二分搜索、迭代法、Newton 法、快速弦截法和弦截法，并用实例在计算机上计算。

三. 实验内容1. 实验题目（1）早在1225年，古代人曾求解方程020102)(23=-++=x x x x f 并给出了高精度的实根368808107.1*=x ，试用Newton 法和弦截法进行验证，要求精度610-=ε，并绘制方程的图形。

答：A.Newton 法：a ．编写文件Newton.m 、func4.m 内容如下所示：b.运行，如下所示A为矩阵，由上面可知，对于初值为5，运行7次即可得到所需的精度，验证结果为古人给出的解释正确的；c.作图，编写下面的文件photo1.m.然后运行即可：注意下面中的x矩阵即为刚才计算出来的x系列，k为迭代的次数：a．编写文件Chord.m内容如下所示：b．运行结果如下所示：由上表可知，在精度为10^-6时有7位有效数字，古人的结果还是正确的c．作图，在上面运行后，即运行newton法时写的photo1.m文件即可出现图像：可以看到图中两条曲线基本重合； （2）取5.00=x ，用迭代法求方程x e x -=的根，然后用Aitken 方法加速，要求精度为结果有4为有效数字。

答：a. 编写文件func7.m 和Aiken.m ，内容如下所示：b ．运行：具有四位有效数字 （3）用快速弦截法求解方程01)(=-=x xe x f ，要求精度为610-=ε，取6.05.010==x x ，作为开始值，并绘制1)(-=x xe x f 的图形。

答：对照可知，书本后面的程序已经正确，运行即可：下面为快速弦截法的主程序文件：函数文件如下：运行如下：作图，编写下面的文件：运行该文件就可以y=x*exp(x)-1函数和插值函数的图：可以看到两条直线基本重合在一起了，扩大图片可以看到两条直线是不重合的：2. 设计思想要求针对上述题目，详细分析每种算法的设计思想。

第04章 方程求根的迭代法

第04章 方程求根的迭代法
其中：n—正整数，x—复变量， a0—an为实、复常数。
定理2：n
次代数方程有 n 个根。
10/74
计算方法——
§4.0 引言
2.

根的分布（有根区间）
求根的隔离区间，定一个[a, b]，使[a, b]内有 且只有一个x*使f(x*)=0 定理3：设函数f(x)在[a, b]内连续，严格单调， 且f(a)*f(b)<0，则在[a, b]内f(x)=0有且仅有一 个实根。 通常有两种做法来确定隔离区间： （1）作y = f(x)的草图，看f(x)在x轴的交点位 臵来定区间[a, b] （2）逐步搜索，在连续区间[a, b]内，选取适 当的x1，x2(a, b)，若f(x1)*f(x2)<0，则[x1, x2] 内有根。
3 2 1 1 3 2 (c ) x g 3 ( x ) 10 x ; 2 1 2


10 (d ) x g4 ( x ) ; 4 x
1 2
x 3 4 x 2 10 (e ) x g5 ( x ) x 3x2 8x
计算方法——
计算方法——
7/74
（3）若f (x)=(x-x*)m
§4.0 引言

例： 代数方程 f ( x ) a n x n a n 1 x n 1 ... a1 x a0 0， n1 超越方程 f ( x ) e x sin x 0
计算方法——
8/74
§4.0 引言
线性的（一次解）
单个方程 代数方程 非线性 多项式（n个解）
超越的（解的数目不定）
线性（一组解） 方程组
非线性（多组解）
f (x)=0根或 f (x)零点，当 f (x)复杂时，很难求

迭代法求根

迭代法求根
(1) 2 2 (1) 2 [ x0 + x= ] a, 即 x0 + 2 x0 x (1) + [ x= ] a.
由于 x (1) 是小量，若省略高阶项 [ x (1) ]2 ，则得校正量 x (1) 的表达式：
1 a 2 x0 + 2 x0 x (1) ≈ a, 即 x (1) ≈ − x0 . 2 x0
由于 x (2) 是小量，若省略高阶项 [ x (2) ]2 ，则得校正量 x (2) 的表达式：
1 a x12 + 2 x1 x (2) ≈ a, 即 x (2) ≈ − x1 . 2 x1
于是方程 x 2 − a = 0 的根的二级近似 x2 为
1 a x2 = x1 + x (2) ≈ + x1 . 2 x1
①
李清扬, 王能超, 易大义. 数值分析[M]. 5 版. 北京: 清华大学出版社, 2008: 14-15. 第 1 页，共 2 页
close all; clc; format compact format long a = 3; x(1) = 2; for i = 1:6 x(i+1) = (1/2)*(a/x(i)+x(i)); disp(['x 的第 ',num2str(i-1),... ' 次迭代的结果为 ',num2str(x(i),'%18.16f\n')]); end h = plot(x); set(h,'LineWidth',1.5) print IterativeMethodSquareRoots.eps -depsc2 -r600 MATLAB x 的第 0 x 的第 1 x 的第 2 x 的第 3 x 的第 4 x 的第 5 执行结果如下。 次迭代的结果为 次迭代的结果为 次迭代的结果为 次迭代的结果为 次迭代的结果为 次迭代的结果为

方程求根的迭代法原理与对比

方程求根的迭代法原理与对比

方程求根的迭代法原理与对比方程求根是数学中常见的问题之一，迭代法是解决方程求根的一种常用方法。

本文将介绍迭代法的原理，并对比几种常见的迭代法，以帮助读者更好地理解和应用于实际问题中。

一、迭代法的原理迭代法是一种通过反复逼近来求解方程根的方法。

其基本思想是从一个初始值开始，通过不断迭代，逐步逼近方程的根。

具体的迭代公式可以表示为：x_(n+1) = f(x_n)其中，x_n 表示第 n 次迭代的值，x_(n+1) 表示第 n+1 次迭代的值，f(x) 表示方程的函数表达式。

通过不断迭代，当 x_n 逐渐接近方程的根时，x_(n+1) 也会越来越接近方程的根。

当两者的差值小于预设的精度要求时，即可认为找到了方程的近似根。

二、常见的迭代法1. 不动点迭代法不动点迭代法是最简单且常见的迭代法之一。

它的迭代公式为：x_(n+1) = g(x_n)其中，g(x) 是一个满足条件的函数，通常通过选取合适的 g(x) 来使得迭代收敛。

例如，对于方程 x^2 - 2 = 0，可以选择 g(x) = sqrt(2 + x)。

2. 牛顿迭代法牛顿迭代法是一种较为高效的迭代法，其迭代公式为：x_(n+1) = x_n - f(x_n)/f'(x_n)其中，f(x) 和 f'(x) 分别表示方程的函数和导数。

牛顿迭代法的关键在于利用函数的切线来逼近方程的根，通过不断迭代，可以快速地找到根的近似值。

3. 弦截法弦截法是一种基于线性插值的迭代法。

其迭代公式为：x_(n+1) = x_n - f(x_n)(x_n - x_(n-1))/(f(x_n) - f(x_(n-1)))弦截法通过连接两个迭代点的直线与 x 轴的交点来逼近方程的根。

相比于牛顿迭代法，弦截法不需要计算导数，适用于一些无法直接求导的函数。

三、迭代法的对比不同的迭代法在收敛速度、稳定性和适用范围上有所差异。

牛顿迭代法通常收敛速度较快，但对于某些特殊情况可能发散；弦截法相对稳定，但收敛速度较慢；不动点迭代法则是最简单但收敛速度相对较慢的方法。

第4章方程求根的迭代方法

第4章方程求根的迭代方法
数值分析简明教程
引论 2+0
第一章 插值方法
第二章 数值积分
8+4
8+2
第三章 常微分方程的差分解法
第四章 方程求根的迭代法
8+4
8+2
第五章 线性方程组的迭代法
第六章 线性方程组的直接法
6+2
8+2
48+16
基本概念
线性方程：未知数都是一次的方程。 非线性方程：高次代数方程和超越方程。 代数方程：由未知数的代数式所组成的方程。
2x
是方程 f ( x) e 1 2 x 2 x 0 的 3 重根。
2x 2
第四章
方程求根的迭代法
4.1 迭代过程的收敛性 4.2 4.3 4.4 迭代过程的加速 牛顿法 弦截法
4.1
4.1.1
迭代过程的收敛性
迭代法的设计思想
有根区间
介 值 定 理 若 函 数 f ( x) 在 [ a , b ] 连 续 ， 且 f ( a ) f ( b ) 0 ，则方程 f ( x ) 0 在 ( a , b ) 内至 少有一个实根。将 [ a , b ] 称为 f ( x ) 的有根区间。
ab )。 2
（4）反复执行第二步与第三步，直到区间长缩小到允许误差范围 之内，此时区间中点即可作为所求的近似解。
例：证明方程 x 3 3 x 2 6 x 1 0 在区间（ 0，1）内有唯一的实根，并 用二分法求这个根的近似值，使误差不超过 0.01 。 解 设 f ( x ) x 3 x 6 x 1, x [0,1] 。因为 f ( x ) 在 [0， 1]连续，且
单根和重根
定理 若 f ( x ) 满足 f ( x ) ( x x )

第4章 方程求根的迭代法

第4章 方程求根的迭代法

' ( x) L
则迭代过程对任意初值x0∈[a,b]均收敛于方程的根x*,且有 下列误差估计式 只要相邻两次 1 x * xk xk 1 xk 迭代值的偏差 1 L 充分小，就能 k L 保证迭代值足 x * xk x1 x0 1 L 够准确。
第4章 方程求根的迭代法
k 2 3 4 5 6 xk 0.54524 0.57970 0.56006 0.57117 0.56486 |xk-xk-1| 0.06129 0.03446 0.01964 0.01111 0.00631 k 7 8 9 10 xk 0.56844 0.56641 0.56756 0.56691 |xk-xk-1| 0.00358 0.00203 0.00115 0.00065
1.89328947 1.89328925 1.89328921 1.89328920 1.89328920 ……
第4章 方程求根的迭代法
2.迭代法收敛的条件 定理1 设 ( x) 在[a,b]上具有连续的一阶导数,且满足下列 两项条件： (1) 对于任意x∈[a,b],总有 ( x)∈[a,b]; (2) 存在0≤L<1,使对于任意x∈[a,b],成立
容易验证，上例迭代18次得到的精度为10-5的结果 为0.56714，本例只要迭代3次即可得到，加速效果明 显.
第4章 方程求根的迭代法
2.埃特金算法 设xk是根x*的某个近似值，用迭代公式校正一次得
xk 1 ( xk )
再迭代一次，得
~ xk 1 ( xk 1 ) x * xk 1 L( x * xk ) x * ~ xk 1 L( x * xk 1 )
1 xk xk 1 (e 0.6 xk ) 1.6

数值分析10-方程求根的迭代法

数值分析10-方程求根的迭代法
ln 2
只要二分足够多次（即 k 充分大），便有
x * xk , 这里 为预定的精度.
例3 用二分法求方程 x3 x 1 0 在区间 [1,1.5] 上的根，误差
限为 102，问至少需对分多少次？
解： a 1, b 1.5， 102;
k ln(b a) ln 1
4.1 方程求根与二分法
4.1.1 引言 单变量非线性方程的一般形式
f (x) 0
（1.1）
其中 x R, f (x) C[a, b], [a, b] 也可以是无穷区间.
f(x)是高次多项式函数或超越函数 如果函数 f (x)是多项式函数，即
f ( x) a0 xn a1 xn1 an1 x an (a0 0), （1.2） 其中 a0 0, ai (i 0,1,, n) 为实数，则称方程(1.1)为n 次代数方程.
• 后来卡当的学生弗瑞里(Ferrari)又提出了四次方程的解法。此成果更 激发了数学家们的情绪，但在以后的二个世纪中，求索工作始终没有 成效，导致人们对高次代数方程解的存在性产生了怀疑。
• 1799年，高斯证明了代数方程必有一个实根或复根的定理，称此为代 数基本定理，并由此可以立刻推理n次代数方程必有n个实根或复根。
超越函数 不能表示为多项式的函数
如 (x)=3x5-2x4+8x2-7x+1 (x)=e2x+1-xln(sinx)-2
高次代数方程
超越方程
如果实数 x *满足 f (x*) 0，则称 x *是方程(1.1)的 根，或称 x *是f (x)的零点.
若f ( x)可分解为 f (x) (x x*)m g (x), 其中 m为正整数，且 g (x*) 0. 则称 x *为方程(1.1)的m 重根，或 x *为 f (x) 的 m重零点，m 1 时为单根. 结论 若 x *是 f (x)的 m重零点，且 g ( x) 充分光滑，则

计算方法 4方程求根的迭代法

计算方法 4方程求根的迭代法

这样,我们总可以假设方程(5―1)(a,b)内有且仅有 一个单实根x*。由连续函数的介值定理知
f(a)·f(b)＜0 若数值b-a较小,那么我们可在(a,b)上任取一点x0作 为方程的初始近似根。
例如,方程
f(x)=x3-x-1=0 由于f(1)＜0,f(1.5)＞0,又f(x)在区间(1,1.5)上单调连 续,故可知在(1,1.5)内有且仅有一个实根。于是可取某 个端点或区间内某一个点的值作为根的初始近似值。
方程的形式很多,我们主要讨论一元非线性方程,也 即
f(x)=0
(5―1)
方程(5―1)可以有实根,也可以有复根或者重根等 。本章主要讨论它的实根的数值计算问题。
方程根的数值计算大致可分三个步骤进行: (1) 判定根的存在性。 (2)确定根的分布范围,即将每一个根用区间隔离 开来。 (3)根的精确化,即根据根的初始近似值按某种方 法逐步精确化,直至满足预先要求的精度为止。
设函数f(x)在区间［a,b］上单调连续,且 f(a)·f(b)＜0
则方程(5―1)在区间(a,b)内有且仅有一个实根x。 下面在有根区间(a,b)内介绍二分法的基本思想。
计算f(a)与f(x0),若 f(a)·f(x0)＜0
则根x∈(a,x0),令
a1=a,b1=x0 否则x∈(x0,b),令
a1=x0,b1=b
该序列必以根x为极限,即
故对于预先给定的精度ε,若有
(5―3)
则结果xk就是方程(5―1)满足预给精度ε的近似根, 也即
由式(5―2)和(5―3)还可得到误差估计式为
(5―4)
对于确定的精度ε,从式(5―4)易求得需要二等分 的次数k。
二分法具有简单和易操作的优点。其计算步骤如 下,框图如图5.3所示。

数值计算_第4章 解线性方程组的迭代法

数值计算_第4章 解线性方程组的迭代法
取初始值：
如果用高斯-赛德尔迭代法 迭代72次得：
用SOR迭代法 ，只须迭代25次即得：
逐次超松弛迭代算法
下列算法假定迭代矩阵收敛，否则要在WHILE循环中增加判断条件。
1．定义和输入系数矩阵 与常数项向量 的元素，输入松弛因子 的值。
2．FOR i:=1,2,…,n
//假定 ，形成常数项向量
FOR
当方程组的系数矩阵 具有某些性质时，可直接判定由它生成的雅可比迭代矩阵是收敛的。
定理4.3若方程组 的系数矩阵 ，满足下列条件之一，则其雅可比迭代法是收敛的。
（1） 为行对角占优阵，即
（2） 为列对角占优阵，即
证明：（1）雅可比迭代矩阵 其中
（2） 为列对角优阵，故 为行对角占优阵，由系数矩阵 构造的迭代矩阵 为行对角占优阵，则有
通常，把 的迭代称为亚松弛迭代，把 的迭代称为高斯-塞德尔迭代，而把 的迭代称为松弛迭代。
4.4
在线性代数中逆矩阵是按其伴随矩阵定义的，若 则方阵 可逆，且 ，其中 为 的伴随矩阵。要计算 个 阶的列式才能得到一个伴随矩阵，在数值计算中因其计算工作量大而不被采用。通常对 做行的初等的效换，在将 化成 的过程中得到 。在数值计算中，这仍然是一种行之有效的方法。
事实上，在计算 前，已经得到 的值，不妨将已算出的分量直接代入迭代式中，及时使用最新计算出的分量值。因此 的计算公式可改为：
即用向量 计算出 的值，用向量 计算出 的值 ，用向量 计算出 的值，这种迭代格式称为高斯—塞德尔迭代。
对于方程组AX=y，如果由它构造高斯-塞德尔迭代和雅可比迭代都收敛，那么，多数情况下高斯—塞德尔迭代比雅可比迭代的收敛效果要好，但是情况并非总是如此。
又
得到
而 ，
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
迭代法是一种重要的数值计算方法，用于求解方程的根。其基本步骤包括：首先将原方程改写成等价形式，并据此构造出相应的迭代公式。接着，选择一个合适的初始近似根，代入迭代公式中进行计算。通过反复迭代，不断校正根的近似值，直至达到预设的精度要求为止。这种方法的关键在于构造一个合适的迭代公式，它能够使迭代过程稳定收敛，并最终逼近真实的根。迭代法的优点在于其通用性和灵活性，可以适用于多种类型的方程求根问题。然而，也需要ቤተ መጻሕፍቲ ባይዱ意选择合适的初始近似根和迭代公式，以确保迭代过程的收敛性和效率。在实际应用中，迭代法常与其他数值解法相结合，以充分发挥各自的优势，提高求解的准确性和效率。