方程求根(计算方法)129页PPT
- 格式:ppt
- 大小:1.80 MB
- 文档页数:129

数学解方程求根解方程求根是数学中的重要内容之一,它在各个领域都有广泛的应用。
通过解方程,我们可以确定未知数的值,从而解决实际问题。
本文将介绍解一元方程、二元方程及高次方程求根的方法。
一、解一元方程一元方程是指只含有一个未知数的方程,如:2x + 3 = 9。
解一元方程的基本步骤如下:1. 整理方程:将方程的所有项移到等号的一侧,使等号左边的表达式为0。
对于示例方程,我们可以写作2x - 6 = 0。
2. 消去系数:将方程中的系数化简为整数。
对于示例方程,我们可以将方程化简为x - 3 = 0。
3. 移项求解:将移项后的方程通过加减法和乘除法等运算得到未知数的解。
对于示例方程,我们可以得到x = 3。
二、解二元方程二元方程是指含有两个未知数的方程,如:2x + 3y = 9。
解二元方程的方法有多种,以下介绍几种常用的方法:1. 代入法:选取其中一个方程,将另一个未知数用该方程中的未知数表示,然后代入另一个方程中求解。
这样可以将二元方程化简为一元方程。
例如,对于方程组2x + 3y = 9和x - y = 1,我们可以通过代入法将y表示为y = x - 1,然后代入第一个方程求解。
2. 消元法:通过加减法将两个方程相加或相减,从而消除一个未知数,得到一个一元方程。
例如,对于方程组2x + 3y = 9和x - y = 1,我们可以通过消元法得到5x = 10,然后解一元方程求解出x的值,再代入原方程求解出y的值。
3. 矩阵法:将方程组的系数矩阵与未知数矩阵相乘,得到与等号右侧常数矩阵相等的新矩阵。
然后通过矩阵运算得到未知数的值。
这种方法适用于较复杂的方程组。
三、解高次方程高次方程是指次数大于等于2的方程,如:x^2 - 4x + 3 = 0。
解高次方程的方法有多种,以下介绍两种常用的方法:1. 因式分解法:将方程化简为多个一次或二次因式相乘的形式,然后分别求解出每个因式等于0时的未知数的值。
例如,对于方程x^2 - 4x + 3 = 0,我们可以将其因式分解为(x - 1)(x - 3) = 0,然后得到x = 1或x = 3。

求根公式公式法
求根公式是一种用来求解一元二次方程(ax^2+bx+c=0)的方法。
它由欧拉在16世纪提出,并且在数学和实际应用中都有重要的地位。
一元二次方程的求根公式如下:
x=(b±√(b^24ac))/(2a)
其中,a、b和c分别代表二次项、一次项和常数项的系数,±表示两个解。
这个公式被称为二次方程的求根公式或者根式公式。
使用求根公式的步骤如下:
1.将一元二次方程化简为标准形式,确保系数已经排列好。
2.根据方程中的系数a、b和c,计算出Δ(即判别式,
Δ=b^24ac)。
3.判断Δ的值:
若Δ>0,方程有两个不相等的实数根,可以使用求根公式计算根的值。
若Δ=0,方程有两个相等的实数根,使用求根公式计算根的值时,两个解会重合。
若Δ<0,方程没有实数根,但是有两个共轭复数根,使用求根公式计算根的值时,会涉及到虚数。
根据上述步骤,我们可以使用求根公式来解决一元二次方程的问题。
这个公式的推导过程涉及一些数学原理,超出了本回答的范围,所以我们只介绍了最终的求根公式和使用方法。
如果你想了解更多关于求根公式的数学原理和推导过程,可以参考相关的教材或者网上的学习资源。




求根公式法
求根公式法是一种解决非线性方程组的数学方法,它利用函数f(x)和它的导数f'(x)来构造一个特殊的多项式P(x),使得P(x)=0时,x就是原方程所要求的根。
它是一种重要的数学工具,在数学建模中有广泛的应用。
求根公式法的基本思想是将原方程f(x)=0转化为一个比较容易求解的表达式:P(x)=0,这里P(x)是一个多项式,它的定义如下:
P(x) = f(x) + xf′(x)
即,把原方程的右端的常数项加上x乘以方程的导数,然后遍历x的每一个值,求出P(x),当P(x)=0时,x 即为原方程的根。
因此,求根公式法就是一种迭代法,我们只需要采用不同的初值,然后不断更新,最终求出一组方程的根。
当然,还需要考虑一些问题,比如收敛性,算法的精度等。
求根公式法的优势在于它的简单性,而它的缺点也非常明显:求根公式法虽然简单,但它的收敛性和精度都不能保证。
它的收敛性取决于初值的选择,如果初值不合适,那么迭代的结果可能会收敛到一个偏差很大的值,甚至不收敛。
而精度则取决于迭代次数,如果迭代次数太少,那么精度也会受到影响。
求根公式法是一种解决非线性方程组的有效方法,尤其是对于不容易直接求解的方程,它能够有效地求解出精确的结果。
此外,它也适用于解决更复杂的方程,比如常微分方程、积分方程等。
总之,求根公式法是一种简单易用的数学工具,它的应用范围很广,可以用来解决复杂的非线性方程组,是数学建模中的重要工具。

求根公式法一、知识概述1、一元二次方程的求根公式将一元二次方程ax2+bx+c=0(a≠0)进行配方,当b2-4ac≥0时的根为.该式称为一元二次方程的求根公式,用求根公式解一元二次方程的方法称为求根公式法,简称公式法.说明:(1)一元二次方程的公式的推导过程,就是用配方法解一般形式的一元二次方程ax2+bx+c=0(a≠0);(2)由求根公式可知,一元二次方程的根是由系数a、b、c的值决定的;(3)应用求根公式可解任何一个有解的一元二次方程,但应用时必须先将其化为一般形式.2、一元二次方程的根的判别式(1)当b2-4ac>0时,方程有两个不相等的实数根;(2)当b2-4ac=0时,方程有两个相等的实数根;(3)当b2-4ac<0时,方程没有实数根.二、重难点知识1、对于一元二次方程的各种解法是重点,难点是对各种方法的选择,突破这一难点的关键是在对四种方法都会使用的基础上,熟悉各种方法的优缺点。
(1) “开平方法”一般解形如“”类型的题目,如果用“公式法”就显得多余的了。
- 1 -(2)“因式分解法”是一种常用的方法,一般是首先考虑的方法。
(3) “配方法”是一种非常重要的方法,一般不使用,但若能恰当地使用,往往能起到简化作用,思考于“因式分解法”之后,“公式法”之前。
如方程;用因式分解,则6391这个数太大,不易分解;用公式法,也太繁;若配方,则方程化为,就易解,若一次项系数中有偶因数,一般也应考虑运用。
(4)“公式法”是一般方法,只要明确了二次项系数、一次项系数及常数项,若方程有实根,就一定可以用求根公式求出根,但因为要代入(≥0)求值,所以对某些特殊方程,解法又显得复杂了。
2、在运用b2-4ac的符号判断方程的根的情况时,应注意以下三点:(1)b2-4ac是一元二次方程的判别式,即只有确认方程为一元二次方程时,才能确定a、b、c,求出b2-4ac;(2)在运用上述结论时,必须先将方程化为一般形式,以便确认a、b、c;(3)根的判别式是指b2-4ac,而不是三、典型例题讲解例1、解下列方程:(1); (2);(3).分析:用求根公式法解一元二次方程的关键是找出a、b、c的值,再代入公式计算,解:(1)因为a=1,,c=10- 2 -所以所以(2)原方程可化为因为a=1,,c=2所以所以.(3)原方程可化为因为a=1,,c=-1所以所以;所以.总结:- 3 -(1)用求根公式法解一元二次方程首先将方程化为一般形式;如果二次项系数为负数,通常将其化为正数;如果方程的系数含有分母,通常先将其化为整数,求出的根要化为最简形式;(2)用求根公式法解方程按步骤进行.例2、用适当方法解下列方程:① ②③ ④⑤ ⑥分析:要合理地选用适当的方法解一元二次方程,就必须熟悉各种方法的优缺点,处理好特殊方法和一般方法的关系。

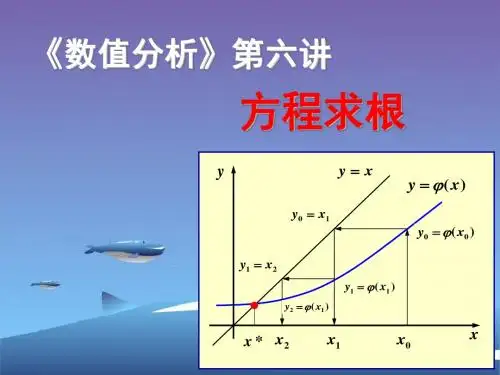

解方程求根公式法解方程求根公式法是数学中一种重要的方法,它可以用来求解各种类型的方程,比如一元二次方程、三次方程、四次方程等等。
本文将详细介绍解方程求根公式法的原理、步骤和应用。
一、原理解方程求根公式法的原理是基于代数运算的基本定理和根的概念。
对于一个一元n次方程 a_n x^n + a_{n-1} x^{n-1} + ... + a_1 x + a_0 = 0,其中a_n ≠ 0,我们可以通过求解它的根来解方程。
如果该方程的根为 x_1,x_2,...,x_n,则有:a_n (x-x_1)(x-x_2)...(x-x_n) = a_n x^n - (a_n x^{n-1})(x_1 + x_2 + ... + x_n) + ... + (-1)^n a_0由代数运算基本定理可知,左边的乘积展开式中,x^n 的系数为1,且各项系数为整数。
因此,我们可以将该方程转化为a_n x^n - (a_n x^{n-1})(x_1 + x_2 + ... + x_n) + ... + (-1)^n a_0 = 0 的形式,然后通过求解根的和、积、差等运算,得到解方程的根。
二、步骤解方程求根公式法的步骤通常如下:1.将一元n次方程化为标准形式,即a_n x^n + a_{n-1} x^{n-1}+ ... + a_1 x + a_0 = 0。
2.根据方程的次数和系数,选择适当的求根公式。
例如,对于一元二次方程a x^2 + b x + c = 0,我们可以使用公式x = (-b ± √(b^2 - 4ac)) / 2a 来求解。
3.代入系数,按照公式计算根的值。
4.检查解的合法性,即检查解是否满足原方程。
5.如果有多个根,重复步骤3-4即可。
三、应用解方程求根公式法在实际应用中非常广泛,比如在物理、工程、金融等领域都有重要的应用。
以下是一些常见的例子:1.一元二次方程的求解。
例如,求解方程 x^2 + 2x - 3 = 0 的根。
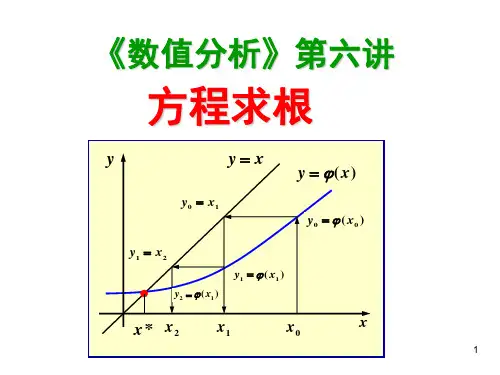
求根公式法一、知识概述1、一元二次方程的求根公式将一元二次方程ax2+bx+c=0(a≠0)进行配方,当b2-4ac≥0时的根为.该式称为一元二次方程的求根公式,用求根公式解一元二次方程的方法称为求根公式法,简称公式法.说明:(1)一元二次方程的公式的推导过程,就是用配方法解一般形式的一元二次方程ax2+bx+c=0(a≠0);(2)由求根公式可知,一元二次方程的根是由系数a、b、c的值决定的;(3)应用求根公式可解任何一个有解的一元二次方程,但应用时必须先将其化为一般形式.2、一元二次方程的根的判别式(1)当b2-4ac>0时,方程有两个不相等的实数根;(2)当b2-4ac=0时,方程有两个相等的实数根;(3)当b2-4ac<0时,方程没有实数根.二、重难点知识1、对于一元二次方程的各种解法是重点,难点是对各种方法的选择,突破这一难点的关键是在对四种方法都会使用的基础上,熟悉各种方法的优缺点。
(1) “开平方法”一般解形如“”类型的题目,如果用“公式法”就显得多余的了。
- 1 -(2)“因式分解法”是一种常用的方法,一般是首先考虑的方法。
(3) “配方法”是一种非常重要的方法,一般不使用,但若能恰当地使用,往往能起到简化作用,思考于“因式分解法”之后,“公式法”之前。
如方程;用因式分解,则6391这个数太大,不易分解;用公式法,也太繁;若配方,则方程化为,就易解,若一次项系数中有偶因数,一般也应考虑运用。
(4)“公式法”是一般方法,只要明确了二次项系数、一次项系数及常数项,若方程有实根,就一定可以用求根公式求出根,但因为要代入(≥0)求值,所以对某些特殊方程,解法又显得复杂了。
2、在运用b2-4ac的符号判断方程的根的情况时,应注意以下三点:(1)b2-4ac是一元二次方程的判别式,即只有确认方程为一元二次方程时,才能确定a、b、c,求出b2-4ac;(2)在运用上述结论时,必须先将方程化为一般形式,以便确认a、b、c;(3)根的判别式是指b2-4ac,而不是三、典型例题讲解例1、解下列方程:(1); (2);(3).分析:用求根公式法解一元二次方程的关键是找出a、b、c的值,再代入公式计算,解:(1)因为a=1,,c=10- 2 -所以所以(2)原方程可化为因为a=1,,c=2所以所以.(3)原方程可化为因为a=1,,c=-1所以所以;所以.总结:- 3 -(1)用求根公式法解一元二次方程首先将方程化为一般形式;如果二次项系数为负数,通常将其化为正数;如果方程的系数含有分母,通常先将其化为整数,求出的根要化为最简形式;(2)用求根公式法解方程按步骤进行.例2、用适当方法解下列方程:① ②③ ④⑤ ⑥分析:要合理地选用适当的方法解一元二次方程,就必须熟悉各种方法的优缺点,处理好特殊方法和一般方法的关系。