计算方法第2章方程求根(1)

第二章 方程求根
一、填空题
1、3 ()2510f x x x =−−=用二分法求方程在区间[1，3]内的根，进行
一步后根所在区间为（ ），进行两步后根所在区间为（ ）。

2、解方程()0f x =的简单迭代法的迭代函数()x ϕ满足在有根区间内
( )，则在有根区间内任意取一点作为初始值，迭代解都收敛。

3、设)(x f 可微，求方程)(x f x =根的牛顿迭代格式是( )。

二、问答题
1、用牛顿法求方程30()10 1.5f x x x x =−−==在附近的一个根，并精确到6位有效数字。

[]42,
11,2x x =−2.给定方程（）试说明该方程在内有根；
（2）构造一个求此根的收敛的迭代法，并说明理由。

3、给定方程()(1)10x f x x e =−−= 1） 分析该方程存在几个根；
2） 用迭代法求出这些根，精确至5位有效数；
3） 说明所用的迭代格式是收敛的。

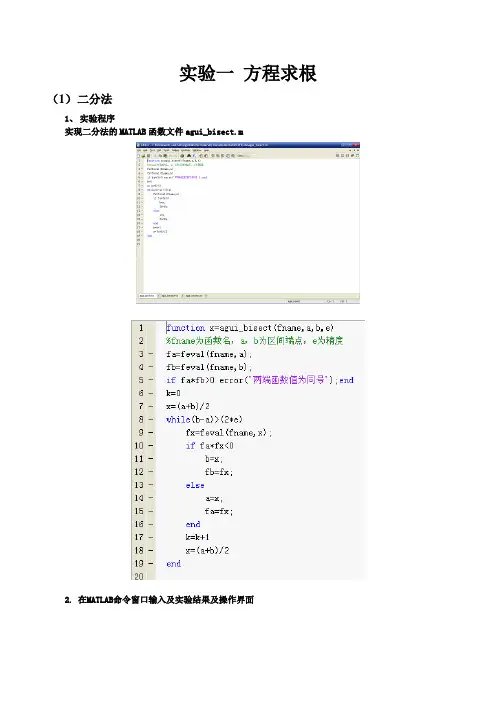
实验一方程求根（1）二分法
1、实验程序
实现二分法的MATLAB函数文件agui_bisect.m
2. 在MATLAB命令窗口输入及实验结果及操作界面
（2）迭代法
1、实验程序
实现二分法的MATLAB函数文件agui_iterative.m
2、在MATLAB命令窗口输入及实验结果及操作界面
（3）牛顿法
1、实验程序
实现二分法的MATLAB函数文件agui_newton.m
2、在MATLAB命令窗口输入及实验结果及操作界面
结果分析：
由上面的对二分法、迭代法、牛顿法三种方法的三次实验结果，我们可以得出这样的结论：
二分法要循环k=10次，迭代法要迭代k=4次，牛顿法要迭代k=2次才能达到精度为0.5*10^-3的要求，而且方程0210=-+x e x
的精确解经计算，为0.0905250,由此可知，牛顿法和迭代法的精确度要优越于二分法。

而这三种方法中，牛顿法不仅计算量少，而且精确度高。

从而可知牛顿迭代法收敛速度明显加快，但由所学的内容可知，其收敛性与初值有关，它是局部收敛的。

二分法收敛虽然是速度最慢，但也常用于求精度不高的近似根。

而迭代法是逐次逼近的方法,原理简单,但存在收敛性和收敛速度的问题。

总之各种方法都各有优劣，适用于不同的情况中，须具体情况具体分析。

第二章 方程求根在许多实际问题中，常常会遇到方程f(x)=0求解的问题。

当f(x)为一次多项式时，f(x)=0称为线性方程，否则称为非线性方程。

对于非线性方程，由于f(x)的多样性，求其根尚无一般的解析方法可以使用，因此研究非线性方程的数值解法是十分必要的。

法、迭代法、牛顿法及割线法。

这些方法均是知道根的初始近似值后，进一步把根精确化，直到达到所要求的 精度为止。

也即求非线性方程根的数值方法。

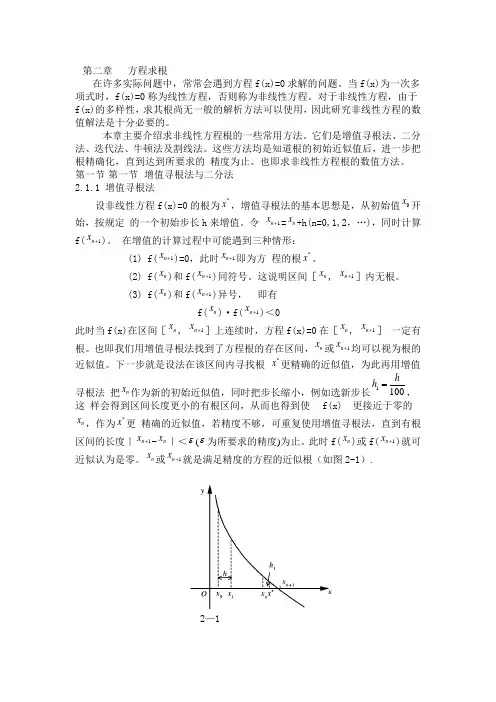
第一节 第一节 增值寻根法与二分法2.1.1 增值寻根法设非线性方程f(x)=0的根为*x ，增值寻根法的基本思想是，从初始值0x 开始，按规定 的一个初始步长h 来增值。

令 1n x +=n x +h(n=0,1,2，…)，同时计算f(1n x +)。

在增值的计算过程中可能遇到三种情形：(1) f(1n x +)=0，此时1n x +即为方 程的根*x 。

(2) f(n x )和f(1n x +)同符号。

这说明区间［n x , 1n x +］内无根。

(3) f(n x )和f(1n x +)异号，f(n x )·f(1n x +)＜0此时当f(x)在区间［n x , 1n x +］上连续时，方程f(x)=0在［n x , 1n x +］ 一定有根。

也即我们用增值寻根法找到了方程根的存在区间，n x 或1n x +均可以视为根的近似值。

下一步就是设法在该区间内寻找根 *x 更精确的近似值，为此再用增值寻根法 把n x 作为新的初始近似值，同时把步长缩小，例如选新步长1100h h =，这 样会得到区间长度更小的有根区间，从而也得到使f(x)n x ，作为*x 更 精确的近似值，若精度不够，可重复使用增值寻根法，直到有根区间的长度｜1n x +-n x ｜＜ε(ε为所要求的精度)为止。

此时f(n x )或f(1n x +)就可近似认为是零。

n x 或1n x +就是满足精度的方程的近似根（如图2-1）.2—1例1 用增值寻根法求方程f(x)=324x x +-10=0的有根区间。

第一章求根公式法：#include<stdio.h>#include<math.h>main(){int a,b,c;double x1,x2,d=0.0;printf("请输入a，b，c的值:\n");scanf("%d,%d,%d",&a,&b,&c);d=b*b-4*a*c;if(d>=0){if(d>0){x1=(-b+sqrt(d))/(2*a);x2=(-b-sqrt(d))/(2*a);printf("方程的两根为x1=%f,x2=%f\n",x1,x2);}else{ x1=-b/(2*a);x2=x1;printf("方程的两根为x1=%f,x2=%f\n",x1,x2);}}else{printf("方程无实根\n");}return 0;}二分法：#include<stdio.h>#include<math.h>double f(double x){double y;y=x*x*x-2*x-5;return y;}main(){double a=2.0,b=3.0,x;if(f(a)*f(b)<0.0){do{x=(a+b)/2.0;if(f(a)*f(x)<0.0){b=x;continue;}if(f(x)*f(b)<0.0)a=x;}while(fabs(a-b)>0.01);}else printf("没有实根");printf("实根为%f",x);return 0;}第二章拉格朗日插值：#include <iostream>#include <iomanip>#include <stdlib.h>using namespace std;#define N 100void lagrange(){int n,k,m,q=1;float x[N],y[N],xx,yyy1,yyy2,yy1,yy2,yy3;cout<<"请输入X的个数：";cin>>n;for(k=0;k<=n-1;k++){cout<<"请输入X"<<k<<"的值：";cin>>x[k];cout<<"请输入Y"<<k<<"的值：";cin>>y[k];}system("cls");cout<<"则Xi与Yi表格如下："<<endl;cout<<"Xi"<<"";for(k=0;k<=n-1;k++)cout<<setiosflags(ios::left)<<setw(10)<<x[k]; cout<<endl;cout<<"Yi"<<"";for(k=0;k<=n-1;k++)cout<<setiosflags(ios::left)<<setw(10)<<y[k]; cout<<endl;while(q){cout<<"请输入所求x的值：";cin>>xx;while(xx>x[k-1]||xx<x[0]){cout<<"输入错误，请重新输入：";cin>>xx;}for(k=0;k<=n-1;k++){if(xx<x[k]){m=k-1;k=n-1;}}yyy1=y[m]*((xx-x[m+1])/(x[m]-x[m+1]))+y[m+1]*((xx-x[m])/(x[m+1]-x[m] ));cout<<"则拉格朗日分段线性插值为："<<yyy1<<endl;for(k=0;k<=n-1;k++){if(xx<x[k]){m=k-1;k=n-1;}}if((xx-x[m])>(x[m+1]-xx))m=m+1;else m=m;yy1=y[m-1]*((xx-x[m])*(xx-x[m+1]))/((x[m-1]-x[m])*(x[m-1]-x[m+1])); yy2=y[m]*((xx-x[m-1])*(xx-x[m+1]))/((x[m]-x[m-1])*(x[m]-x[m+1])); yy3=y[m+1]*((xx-x[m-1])*(xx-x[m]))/((x[m+1]-x[m-1])*(x[m+1]-x[m])); yyy2=yy1+yy2+yy3;cout<<"则拉格朗日分段二次插值为："<<yyy2<<endl;cout<<"是否输入其余要求x的值[是(1)，否(0)]：";cin>>q;}system("cls");}void main(){lagrange();}牛顿插值：#include<stdio.h>#include<math.h>main(){float a[]={0,1,2,3,4},b[]={3,6,11,18,27};float f[5],x,t,m,n,s=0;int i,j,k,l;printf("请输入x的值：");scanf("%f",&x);f[0]=b[0];for(i=1;i<5;i++){m=0;for(j=0;j<=i;j++){t=1;for(k=0;k<=i;k++){if(k!=j) t=t/(a[j]-a[k]);}m=m+b[j]*t;}n=1;for(l=0;l<i;l++) n=n*(x-a[l]);s=s+m*n;}s=s+f[0];printf("s=%f",s);return 0;}线性和二次插值法：#include<stdio.h>#include<math.h>main(){floata[]={0.4,0.5,0.6,0.7,0.8,0.9},b[]={-0.916291,-0.693147,-0.510826,-0.3566 75,-0.223144,-0.105361};float x,t,m,p1=0.0,p2=0.0,p3=0.0;int i,j;printf("请输入x的值");scanf("%f",&x);for(i=0;i<2;i++){t=0.0;for(j=0;j<2;j++){if(j!=i) t=t+((x-a[j])/(a[i]-a[j]))*b[i];}p1=p1+t;}printf("线性插值的结果为:%f",p1);for(i=0;i<3;i++){m=1.0;for(j=0;j<3;j++){if(j!=i) m=m*((x-a[j])/(a[i]-a[j]));}p2=p2+m*b[i];}printf("取0.4，0.5，0.7，的二次插值的结果为:%f",p2); for(i=1;i<4;i++){m=1.0;for(j=1;j<4;j++){if(j!=i) m=m*((x-a[i])/(a[i]-a[j]));}p3=p3+m*b[i];}printf("取0.5，0.6，0.7的二次插值的结果为:%f",p3);return 0;}直线拟合法：#include<stdio.h>#include<math.h>main(){float X[5]={-2,-1,0,1,2},Y[5]={0,0.2,0.5,0.8,1.0}; float a=0,b=0,c=0,d=0,m,n;int i;for(i=0;i<5;i++){a=a+X[i];b=b+Y[i];c=c+X[i]*X[i];d=d+X[i]*Y[i];};m=(b*c-a*d)/(5*c-a*a);n=(5*d-c*a)/(5*c-a*a);float x,y;printf("请输入X的值");scanf("%f",&x);y=m+n*x;printf("拟合后代入x的值得出的结果为:%f",y); return 0;}第三章复化辛甫生算法：#include<stdio.h>#include<math.h>float f(float x){float y;y=3*x*x+2*x;return y;}main(){float a,b,h,s;int k=1,n;printf("请输入a,b,n");scanf("%f,%f,%d",&a,&b,&n);h=(b-a)/n;s=f(b)-f(a);for(float x=a;k<n;k++){x=x+h/2;s=s+4*f(x);x=x+h/2;s=s+2*f(x);}s=(h/6)*s;printf("s=%f",s);}龙贝格算法：#include<stdio.h>#include<string.h>#include<math.h>#include<conio.h>#include<stdlib.h>float f(float x){return (2*x);}float r(float a,float b){int k=1;float s,x,t1,t2,s1,s2,c1,c2,r1,r2,h=b-a,p;t1=h*(f(a)+f(b))/2;while(1){s=0;x=a+h/2;do{s+=f(x);x+=h;}while(x<b);t2=(t1+h*s)/2.0;if(fabs(t2-t1)<p)return(t2);s2=t2+(t2-t1)/3.0;if(k==1){t1=t2;s1=s2;h/=2;k+=1;continue;}c2=s2+(s2-s1)/15.0;if(k==2){c1=c2;t1=t2;s1=s2;h/=2.0;k+=1;continue;}r2=c2+(c2-c1)/63;if(k==3){r1=r2;c1=c2;t1=t2;s1=s2;h/=2;k+=1;continue;};if(fabs(s1-s2)<p)return(s2);r1=r2;c1=c2;t1=t2;s1=s2;h/2;k+=1;return(r1);}}main(){int i;float a,b,p,s,clrsca();printf("\n input integrate f(x) the begin:");scanf("%f",&a);printf("\n input integrate f(x) the end:"); scanf("%f",&b);printf("\n input p:");scanf("%f",&p);s=r(a,b);printf("the result is:%f",s);getch();return(s);}变步长积分法：#include<stdio.h>#include<math.h>void main(){double k,a,b;int kk,n;double sum[100],t[100];printf("方程为f(x)=x/(4+x^2),积分区间为[0,1]\n");printf("请输入预定精度a的值\n");scanf("%lf",&a);t[0]=0.1;t[1]=0.1088;for(k=1.0,kk=1;fabs(t[kk]-t[kk-1])>=a;k++,kk++){for(n=1,sum[kk+1]=0;n<=pow(2.0,k);n++){b=(2*n-1)/pow(2.0,k+1);sum[kk+1]+=b/(4+b*b);}t[kk+1]=0.5*t[kk]+(1/pow(2.0,k+1))*sum[kk+1];}printf("\n方程利用变步长梯形法积分后的积分值为%f\n",t[kk]);}第四章：欧拉法：#include<stdio.h>#include<math.h>#include<string.h> #include<stdlib.h> float f(float x,float y){ float f;f=x+y;return f;};main(){float x[6],y[6],h;int n;printf("请输入x[0],y[0],h的值:");scanf("%f%f%f",&x[0],&y[0],&h);for(n=1;n<6;x[0]=x[n],y[0]=y[n],n++){ x[n]=x[0]+h;y[n]=y[0]+h*f(x[0],y[0]);printf("%f,%f",x[n],y[n]);printf("\n");}return 0;}改进欧拉法：#include<stdio.h>#include<math.h>#include<string.h>#include<stdlib.h>float f(float x,float y){float f;f=x+y;return f;};main(){float x[6],y[6],h,yp,ye;int n;printf("请输入x[0],y[0],h的值:");scanf("%f%f%f",&x[0],&y[0],&h);for(n=1;n<6;x[0]=x[n],y[0]=y[n],n++){ x[n]=x[0]+h;yp=y[0]+h*f(x[0],y[0]);ye=y[0]+h*f(x[n],yp);y[n]=(yp+ye)/2;printf("%f,%f",x[n],y[n]);printf("\n");}return 0;}四阶龙格库塔法：#include<stdio.h>#include<math.h>#include<string.h>float f(float x,float y){float f;f=x+y;return f;}main(){float x[11],y[11],h,k1,k2,k3,k4;printf("请分别输入x[0],y[0],h的值：");scanf("%f%f%f",&x[0],&y[0],&h);for(int n=1;n<11;x[0]=x[n],y[0]=y[n],n++){ x[n]=x[0]+h;k1=f(x[0],y[0]);k2=f(x[0]+h/2,y[0]+h*k1/2);k3=f(x[0]+h/2,y[0]+h*k2/2);k4=f(x[n],y[0]+h*k3);y[n]=y[0]+h*(k1+2*k2+2*k3+k4)/6;printf("%f,%f",x[n],y[n]);printf("\n");}return 0;}第六章迭代法：#include<stdio.h>#include<math.h>#include<string.h>double F1(double x);double Newton(double x0, double e); int main(){double x0 = 0.5;double e = 10E-6;printf("x = %f\n", Newton(x0, e));getchar();return 0;}double F1(double x){return log(x+2)/log(10);}double Newton(double x0, double e) {double x1;do{x1 = x0;x0 =F1(x1);} while (fabs(x0 - x1) > e);return x0;}埃特金加速法：#include<stdio.h>#include<conio.h>#include<math.h>#define h 1.E-10 double f(double x0) {x0=exp(-x0);return x0;}double sub(double x) {if(x>=0)return x;else return -x;}main(){double x0=0.5,x,s=0.0; do{x=f(x0);s=sub(x-x0);x0=x;}while(s>h); printf("x=%f",x); getch();return 0;}快速弦截法：#include<stdio.h>#include <math.h>float f(float x){float y;y=x*exp(x)-1;return (y);}float xpoint(float x1,float x2){float y;y=(x1*f(x2)-x2*f(x1)) / (f(x2) - f(x1));return (y) ;}float root(float x1, float x2) {int i;float x,y,y1;y1=f(x1);do{x=xpoint(x1,x2);y=f(x);if(y*y1>0){y1=y;x1=x;}elsex2=x;}while(fabs(y)>=0.0000001); return (x);}main(){float x1,x2,f1,f2,x;do{printf("input x1,x2:\n");scanf("%f,%f",&x1,&x2);f1=f(x1);f2=f(x2);}while(f1*f2>=0);x=root(x1,x2);printf("A root of equation is %8.4f\n",x); }第七章高斯消去法：#include<stdio.h>#include<math.h>main(){float a[10][10],b[10],m[10][10],x[10],sum; int i,j,k,n;printf("the top exp:");scanf("%d",&n);printf("\n");for(i=0;i<n;i++){for(j=0;j<n;j++){scanf("%f",&a[i][j]);}for(i=0;i<n;i++){scanf("%f",&b[i]);}for(k=0;k<n-1;k++){if(a[k][k]==0)printf("error");else {for(i=k+1;i<n;i++){m[i][k]=a[i][k]/a[k][k];} };a[i][k]=m[i][k];b[i]=b[i]-m[i][k]*b[k];for(j=k+1;j<n;j++)a[i][j]=a[i][j]-m[i][k]*a[k][j];};if(a[n-1][n-1]==0)printf("error");else x[n-1]=b[n-1]/a[n-1][n-1];b[n-1]=x[n-1];for(i=n-2;i>=0;i--){sum=0;for(j=i+1;j<n;j++){sum+=a[i][j]*x[j];}x[i]=(b[i]-sum)/a[i][i];b[i]=x[i];}for(i=0;i<n;i++)printf("%f\n",x[i]);}return 0;}选主元消去法：#include<stdio.h>#include<math.h>main(){float a[10][10],b[10],s,t,e,sum; int i,j,k,n,m;printf("The top exp is "); scanf("%d",&n);for(i=0;i<n;i++)for(j=0;j<n;j++)scanf("%f",&a[i][j]);for(i=0;i<n;i++)scanf("%f",&b[i]);scanf("%f",&e);k=0;do{t=a[k][k];for(i=k;i<n;i++){if(fabs(t)<fabs(a[i][k])){t=a[i][k];m=i;}else m=k;}if(fabs(t)<e)printf("det A = 0\n");else {if(m!=k){for(j=0;j<n;j++){s=a[m][j];a[m][j]=a[k][j];a[k][j]=s;}s=b[m];b[m]=b[k];b[k]=s;}for(i=k+1;i<n;i++)for(j=k+1;j<n;j++){a[i][k]=a[i][k]/a[k][k];a[i][j]=a[i][j]-a[i][k]*a[k][j];b[i]=b[i]-a[i][k]*b[k];}}k++;}while(k<n-2);if(fabs(a[n-1][n-1])<e)printf("det A = 0\n");else {b[n-1]=b[n-1]/a[n-1][n-1];for(i=n-2;i>=0;i--){sum=0;for(k=i+1;k<n;k++){sum+=a[k][j]*b[j];}b[i]=(b[i]-sum)/a[i][i];}}for(i=0;i<n;i++)printf("%f\n",b[i]);}追赶法：#include<stdio.h>#include<math.h>main(){int i,j,k,n;float d[10][10],g[10],a[10],b[10],c[10],x[10],y[10],f[10];printf("the top exp is ");scanf("%d",&n);scanf("%f,%f,%f,%f",&d[0][0],&d[0][1],&d[n-1][n-2],&d[n-1][n-1]); for(i=1;i<n-1;i++)for(j=i-1;j<=i+1;j++)scanf("%f",&d[i][j]);for(i=0;i<n;i++)scanf("%f",&g[i]);for(i=1;i<n-1;i++)a[i]=d[i][i-1];for(i=0;i<n;i++)b[i]=d[i][i];for(i=0;i<n-1;i++)c[i]=d[i][i+1];f[0]=c[0]/b[0];for(k=1;k<n-1;k++)f[k]=c[k]/(b[k]-a[k]*f[k-1]);y[0]=g[0]/b[0];for(i=1;i<n;i++)y[i]=(g[i]-a[i]*y[i-1])/(b[i]-a[i]*f[i-1]); x[n-1]=y[n-1];for(i=n-2;i>=0;i--)x[i]=y[i]-f[i]*x[i+1];for(i=0;i<n;i++)printf("%f\n",x[i]);}。

《计算方法》习题答案第一章 数值计算中的误差1．什么是计算方法？（狭义解释）答：计算方法就是将所求的的数学问题简化为一系列的算术运算和逻辑运算，以便在计算机上编程上机，求出问题的数值解，并对算法的收敛性、稳定性和误差进行分析、计算。

2．一个实际问题利用计算机解决所采取的五个步骤是什么？答：一个实际问题当利用计算机来解决时，应采取以下五个步骤： 实际问题→建立数学模型→构造数值算法→编程上机→获得近似结果 4．利用秦九韶算法计算多项式4)(53-+-=x x x x P 在3-=x 处的值，并编程获得解。

解：400)(2345-+⋅+-⋅+=x x x x x x P ，从而 1 0 -1 0 1 -4 -3 -3 9 -24 72 -2191-38-2473-223所以，多项式4)(53-+-=x x x x P 在3-=x 处的值223)3(-=-P 。

5．叙述误差的种类及来源。

答：误差的种类及来源有如下四个方面：（1）模型误差：数学模型是对实际问题进行抽象，忽略一些次要因素简化得到的，它是原始问题的近似，即使数学模型能求出准确解，也与实际问题的真解不同，我们把数学模型与实际问题之间存在的误差称为模型误差。

（2）观测误差：在建模和具体运算过程中所用的一些原始数据往往都是通过观测、实验得来的，由于仪器的精密性，实验手段的局限性，周围环境的变化以及人们的工作态度和能力等因素，而使数据必然带有误差，这种误差称为观测误差。

（3）截断误差：理论上的精确值往往要求用无限次的运算才能得到，而实际运算时只能用有限次运算的结果来近似，这样引起的误差称为截断误差（或方法误差）。

（4）舍入误差：在数值计算过程中还会用到一些无穷小数，而计算机受机器字长的限制，它所能表示的数据只能是一定的有限数位，需要把数据按四舍五入成一定位数的近似的有理数来代替。

这样引起的误差称为舍入误差。

6．掌握绝对误差（限）和相对误差（限）的定义公式。

求根公式二次方程的解法求根公式是解决二次方程的常用方法之一。

二次方程的一般形式为ax^2 + bx + c = 0，其中a、b、c为已知实数，且a ≠ 0。

求根公式可以帮助我们找到二次方程的解，即x的值。

在本文中，将详细介绍求根公式的推导和使用。

推导求根公式：假设二次方程ax^2 + bx + c = 0有两个解x1和x2，我们可以通过下面的步骤来推导求根公式。

步骤1：将二次方程用完全平方的形式表示。

将ax^2 + bx + c = 0移项得ax^2 + bx = -c。

步骤2：将二次方程的左边进行完全平方。

首先，我们需要找到一个常数k，使得(b/2a)^2 = k。

这样，我们可以将ax^2 + bx写成(a(x^2 + (b/2a)x + k) - ak) = -c。

步骤3：继续进行完全平方操作。

我们将x^2 + (b/2a)x + k写成(x + (b/2a))^2 - (b/2a)^2 + k的形式。

步骤4：化简右边的表达式。

(x + (b/2a))^2 - (b/2a)^2 + k = 0可以简化为(x + (b/2a))^2 = (b^2 -4ac)/4a^2 - k。

步骤5：将等式两边开平方。

由于等式两边相等，故(x + (b/2a))^2的值也应该等于(b^2 - 4ac)/4a^2 - k。

步骤6：消去开根号和平方。

令Δ = b^2 - 4ac，即二次方程的判别式。

将上式展开得x + (b/2a) =±√(b^2 - 4ac)/2a - √k。

步骤7：将x孤立我们可以进一步化简得x = (-b ± √Δ)/(2a) - (b/2a)。

这就是二次方程的求根公式。

求根公式的应用：现在我们来解决一个实际问题，通过求根公式来计算二次方程的解。

例题1：解方程2x^2 + 3x - 9 = 0。

根据求根公式，a = 2，b = 3，c = -9。

将这些值代入求根公式x = (-b ± √Δ)/(2a) - (b/2a)中：Δ = b^2 - 4ac = 3^2 - 4 * 2 * (-9) = 105x = (-3 ± √105)/(4) ≈ (1.5 ± 2.45).因此，方程2x^2 + 3x - 9 = 0的解为x ≈ 3.95或x ≈ -2.45。

方程求根§2.0 引言§2.1 二分法§2.2 简单迭代法§2.3 牛顿（Newton）法§2.4 其它求根方法（迭代过程的加速方法）§2.5 作业讲评2.0 引 言非线性科学是当今科学发展的一个重要研究方向，非线性方程的求根也成为其中一个重要内容。

一般而言，非线性方程的求根非常复杂。

在实际应用中有许多非线性方程的例子，例如（1）在光的衍射理论（the theory of diffraction of light)中,需要求x-tanx=0的根（2）在行星轨道（ planetary orbits ）的计算中,对任意的a 和b ，需要求x-asinx=b 的根（3）在数学中，需要求n 次多项式-1-110 ... 0n n n n a x a x a x a ++++=的根。

非线性方程的一般形式 ()0f x = 这里()f x 是单变量x 的函数，它可以是代数多项式-1-110() ... nn n n f x a x a x a x a =++++ (0n a ≠)也可以是超越函数，即不能表示为上述形式的函数。

满足方程 ()0f x = 的x 值通常叫做方程的根或解，也叫函数()0f x =的零点。

2.1 二分法(Bisection Method)1 概念:二分法也称对分区间法、对分法等，是最简单的求根方法，属于区间法求根类型。

在用近似方法时，需要知道方程的根所在区间。

若区间[a,b]含有方程f(x)=0的根，则称[a,b]为f(x)=0的有根区间；若区间[a,b]仅含方程f(x)= 0的一个根，则称[a,b]为f(x)= 0的一个单根区间。

2．基本思想根的存在定理(零点定理)：f(x)为[a,b]上的连续函数，若f(a)·f(b)<0，则[a,b]中至少有一个实根。

如果f(x)在[a,b]上还是单调递增或递减的，则f(x)=0仅有一个实根。

2.1.2 一元二次方程的解集及其根与系数的关系课标要求素养要求1.理解判别式的作用，掌握一元二次方程的解法：因式分解法(包括“十字相乘法”)，配方法和求根公式法(重点).2.掌握一元二次方程根与系数的关系(韦达定理).通过求一元二次方程的解集及根与系数关系的应用，提升逻辑推理和数学运算素养.教材知识探究利用恒等式的变形，推导一元二次方程根与系数的关系如下 设一元二次方程ax 2＋bx ＋c ＝0(a ≠0)两根为x 1，x 2， 令ax 2＋bx ＋c ＝a (x －x 1)(x －x 2)＝ax 2－a (x 1＋x 2)x ＋ax 1x 2， ∴⎩⎨⎧b ＝－a （x 1＋x 2），c ＝ax 1x 2，即⎩⎪⎨⎪⎧x 1＋x 2＝－ba ，x 1x 2＝c a .1.一元二次方程的解集 (1)一般地，方程x 2＝t ：①当t >0时，解集为{t ，－t }； ②当t ＝0时，解集为{0}； ③当t <0时，解集为∅． (2)一般地，方程(x －k )2＝t ：①当t >0时，解集为{k ＋t ，k －t }； ②当t ＝0时，解集为{k }； ③当t <0时，解集为∅．(3)一元二次方程ax 2＋bx ＋c ＝0(a ≠0)的判别式及求根公式判别式只能判定实系数(系数全都是实数)一元二次方程的解集的情况一般地，Δ＝b 2－4ac 称为一元二次方程ax 2＋bx ＋c ＝0(a ≠0)的判别式．对一元二次方程ax 2＋bx ＋c ＝0(a ≠0)，Δ>0⇔有两个不相等的实根；Δ＝0⇔有两个相等的实根；Δ<0⇔无实数根． 当Δ≥0时，x 1＝－b ＋b 2－4ac 2a ，x 2＝－b －b 2－4ac 2a 叫做一元二次方程ax 2＋bx ＋c ＝0(a ≠0)的求根公式．(4)一元二次方程的解集 实系数一元二次方程有实数根的充要条件是Δ≥0 设ax 2＋bx ＋c ＝0(a ≠0) ①当Δ＝b 2－4ac ＞0时，方程的解集为⎩⎭2a ，2a ； ②当Δ＝b 2－4ac ＝0时，方程的解集为⎩⎨⎧⎭⎬⎫－b 2a ；③当Δ＝b 2－4ac ＜0，方程的解集为∅. 是指在实数范围内方程无解． 2.一元二次方程根与系数的关系对任何Δ≥0的一元二次方程，根与系数的关系都成立设x 1，x 2是一元二次方程ax 2＋bx ＋c ＝0(a ≠0)的两根，则有⎩⎨⎧x 1＋x 2＝－b a，x 1x 2＝c a Ｗ.常用的几个变形：①x 21＋x 22＝(x 1＋x 2)2－2x 1x 2； ②(x 1－x 2)2＝(x 1＋x 2)2－4x 1x 2；③x 31＋x 32＝(x 1＋x 2)3－3x 1x 2(x 1＋x 2)； ④|x 1－x 2|＝（x 1－x 2）2＝（x 1＋x 2）2－4x 1x 2； ⑤1x 1＋1x 2＝x 1＋x 2x 1x 2. 教材拓展补遗[微判断]1.ax 2＋bx ＋c ＝0(a ，b ，c 为常数)叫做一元二次方程.(×) 提示 当a ＝0时，不是一元二次方程.2.一元二次方程均可化为(x －k )2＝t 的形式.(√)3.一元二次方程解的情况由一元二次方程的系数完全确定.(√) [微训练]1.下列方程中，是关于x 的一元二次方程的是( ) A.3(x ＋1)2＝2(x ＋1)B.1x 2＋1x －2＝0C.ax 2＋bx ＋c ＝0D.x 2＋2x ＝x 2－1解析 A 中方程可化为3x 2＋4x ＋1＝0，是一元二次方程；B 中方程是关于1x 的一元二次方程；对C ，当a ＝0时，不是关于x 的一元二次方程；D 中方程可化为2x ＝－1，不是一元二次方程. 答案 A2.已知m 是方程x 2－x －1＝0的一个根，则代数式m 2－m 的值等于( ) A.－1 B.0 C.1D.2解析 由题意，m 2－m －1＝0，即m 2－m ＝1. 答案 C3.关于x 的一元二次方程x 2＋px ＋q ＝0的两根分别为x 1＝2，x 2＝1，则p ，q 的值分别为( ) A.－3，2 B.3，－2 C.2，－3D.2，3解析 由根与系数的关系，得⎩⎨⎧2＋1＝－p ，2×1＝q ，∴⎩⎨⎧p ＝－3，q ＝2.答案 A [微思考]一元二次方程(系数均为实数)有两个根，它的解集是否一定有两个元素？ 提示 当一元二次方程的判别式为零时，方程有两个相等的实数根，其解集只有一个元素.题型一 一元二次方程判别式的应用【例1】 试证明：不论m 为何值，方程2x 2－(4m －1)x －m 2－m ＝0总有两个不相等的实数根.证明 ∵Δ＝[－(4m －1)]2－4×2×(－m 2－m )＝24m 2＋1＞0，∴不论m 为何值时，方程2x 2－(4m －1)x －m 2－m ＝0总有两个不相等的实数根. 规律方法 一元二次方程ax 2＋bx ＋c ＝0(a ，b ，c ∈R 且a ≠0)的实数根的情况可由Δ＝b 2－4ac 加以判定，即Δ＞0时，有两不相等的实数根；当Δ＝0时，有两个相等的实数根；当Δ＜0时，没有实数根. 【训练1】 不解方程，判别下列方程根的情况. (1)x 2－14x ＋12＝0；(2)4x 2＋12x ＋9＝0； (3)2x 2－3x ＋6＝0.解 (1)Δ＝(－14)2－4×1×12＝148＞0，∴x 2－14x ＋12＝0有两个不相等的实数根；(2)Δ＝122－4×4×9＝0，∴4x 2＋12＋9＝0有两个相等的实数根； (3)Δ＝(－3)2－4×2×6＝－39＜0，∴2x 2－3x ＋6＝0没有实数根. 题型二 换元法的应用【例2】 求方程1x 2－1x －1＝0的解集.解 令y ＝1x ≠0，则方程1x 2－1x －1＝0可化为y 2－y －1＝0， 由求根公式，得y 1＝1＋52或y 2＝1－52，即1x ＝1＋52或1x ＝1－52， ∴x ＝5－12或x ＝－5＋12，∴原方程的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫－5＋12，5－12. 规律方法 通过引入新元y (y 为关于x 的代数式)，可把一些关于x 的方程化为关于y 的二次方程ay 2＋by ＋c ＝0(a ≠0)，从而求出y 的值，进而求出x 的值. 【训练2】 求下列方程的解集. (1)x 4－3x 2＋2＝0；(2)x ＋2x －1＝0； (3)(x 2－x )2－(x 2－x )－2＝0.解 (1)令y ＝x 2≥0，得y 2－3y ＋2＝0， ∴y ＝1或y ＝2，即x 2＝1或x 2＝2， ∴x ＝±1或x ＝± 2.∴原方程的解集为{－2，－1，1，2}. (2)令y ＝x ≥0，得y 2＋2y －1＝0， ∴y ＝－1＋2或y ＝－1－2(舍).从而x ＝－1＋2，即x ＝3－22， ∴原方程的解集为{3－22}.(3)令x 2－x ＝t ，得t 2－t －2＝0，∴t 1＝－1或t 2＝2， 即x 2－x ＋1＝0 ①或x 2－x －2＝0 ② 对①，Δ＝－3＜0，无实数解；对②，易得x ＝－1或x ＝2，故原方程的解集为{－1，2}. 题型三 一元二次方程根与系数关系的应用【例3】 已知关于x 的一元二次方程x 2－2x ＋m －1＝0有两个实数根x 1，x 2. (1)求m 的取值范围；(2)当x 21＋x 22＝6x 1x 2时，求m 的值.解 (1)由Δ＝(－2)2－4(m －1)＝－4(m －2)≥0，得m ≤2，即m 的取值范围是 (－∞，2].(2)由根与系数的关系，得⎩⎨⎧x 1＋x 2＝2，x 1x 2＝m －1.∵x 21＋x 22＝6x 1x 2，∴(x 1＋x 2)2＝8x 1x 2，即22＝8(m －1)，解得m ＝32.∵32<2，∴m 的值为32.规律方法 运用根与系数的关系，注意两点(1)常见变形x 21＋x 22＝(x 1＋x 2)2－2x 1x 2，|x 1－x 2|＝（x 1＋x 2）2－4x 1x 2；(2)整体代入.【训练3】 已知关于x 的方程x 2－2(k －1)x ＋k 2＝0有两个实数根x 1，x 2. (1)求k 的取值范围；(2)若|x 1＋x 2|＝x 1x 2－1，求k 的值.解 (1)由Δ＝[－2(k －1)]2－4k 2＝4(1－2k )≥0，得k ≤12，即k 的取值范围是⎝ ⎛⎦⎥⎤－∞，12. (2)由根与系数的关系，得⎩⎨⎧x 1＋x 2＝2（k －1），x 1x 2＝k 2.∵|x 1＋x 2|＝x 1x 2－1，∴|2(k －1)|＝k 2－1 ①，∵k ∈⎝ ⎛⎦⎥⎤－∞，12，∴k －1≤－12，∴①可化为－2＝k ＋1，∴k ＝－3.一、素养落地1.通过学习求一元二次方程的解集提升运算素养；通过学习根与系数的关系提升逻辑推理和数学运算素养.2.求一元二次方程解集时，先用判别式判定解的情况再求解集.3.运用根与系数关系时，注意恒等变形和整体代入. 二、素养训练1.用配方法解下列方程时，配方有错误的是( ) A.x 2－2x －99＝0化为(x －1)2＝100 B.x 2＋8x ＋9＝0化为(x ＋4)2＝25 C.2t 2－7t －4＝0化为⎝ ⎛⎭⎪⎫t －742＝8116D.3y 2－4y －2＝0化为⎝ ⎛⎭⎪⎫y －232＝109解析 x 2＋8x ＋9＝0配方应为(x ＋4)2＝7.选B. 答案 B2.如果关于x 的方程ax 2＋x －1＝0有实数根，则a 的取值范围是( ) A.⎝ ⎛⎭⎪⎫－14，＋∞ B.⎣⎢⎡⎭⎪⎫－14，＋∞ C.⎣⎢⎡⎭⎪⎫－14，0∪(0，＋∞) D.⎝ ⎛⎭⎪⎫－14，0∪(0，＋∞) 解析 当a ＝0时，x ＝1，符合题意；当a ≠0时，由Δ＝12＋4a ≥0，得a ≥－14.综上，a 的取值范围为⎣⎢⎡⎭⎪⎫－14，＋∞.答案 B3.已知(x 2＋y 2＋1)(x 2＋y 2－3)＝5，则x 2＋y 2＝________.解析 令t ＝x 2＋y 2≥0，则原方程可化为(t ＋1)(t －3)＝5，即t 2－2t －8＝0. ∴t ＝4或t ＝－2(舍去)，故x 2＋y 2＝4. 答案 44.已知关于x 的方程x 2－kx ＋k －2＝0有两个正实根，则k 的取值范围是________.解析由题意得⎩⎨⎧（－k ）2－4（k －2）≥0，k ＞0，k －2＞0，解得k ＞2.答案 (2，＋∞)5.求作一个一元二次方程，使它的两根分别是方程6x 2－3x －2＝0的两根的平方. 解 设方程6x 2－3x －2＝0的两根为x 1，x 2， 则x 1＋x 2＝12，x 1x 2＝－13.由题意求作方程的两根为x 21，x 22，则x 21＋x 22＝(x 1＋x 2)2－2x 1x 2＝1112，x 21·x 22＝(x 1x 2)2＝19，故求作的一元二次方程为x 2－1112x ＋19＝0， 即为36x 2－33x ＋4＝0.基础达标一、选择题1.解方程(5x －1)2＝3(5x －1)的适当方法是( ) A.开平方法 B.配方法 C.公式法D.因式分解法解析 由(5x －1)2＝3(5x －1)，得(5x －1)(5x －4)＝0，再求解最简单.故选D. 答案 D2.如果x 2＋2(m －2)x ＋9是完全平方式，那么m 的值等于( ) A.5 B.5或－1 C.－1D.－5或－1解析 由题意m －2＝±3，∴m ＝5或m ＝－1. 答案 B3.下列结论正确的是( )A.若x 2＝4，则x ＝2B.若x 2－5xy －6y 2＝0(xy ≠0)，则x y ＝6或xy ＝－1 C.方程x (2x －1)＝2x －1的解集为{1} D.方程x 2－3x ＋2x －1＝0的解集为{1，2}解析 对A ，由x 2＝4，得x ＝±2；对B ，∵xy ≠0，∴方程两边同除以y 2得⎝ ⎛⎭⎪⎫x y 2－5x y －6＝0，∴x y ＝6或xy ＝－1；对C ，方程可化为(2x －1)(x －1)＝0，解集为⎩⎨⎧⎭⎬⎫12，1；对D ，x ＝1时方程无意义.故选B. 答案 B4.已知α，β是一元二次方程x 2－5x －2＝0的两实数根，则α2＋αβ＋β2的值为( ) A.－1 B.9 C.23D.27解析 由根与系数的关系，得⎩⎨⎧α＋β＝5，αβ＝－2，则α2＋αβ＋β2＝(α＋β)2－αβ＝52＋2＝27. 答案 D5.小明和小华解同一个一元二次方程时，小明看错一次项，解得两根为2，－3，而小华看错常数项，解得两根为－2，5，那么原方程为( ) A.x 2－3x ＋6＝0 B.x 2－3x －6＝0 C.x 2＋3x －6＝0D.x 2＋3x ＋6＝0解析 设原方程为x 2＋mx ＋n ＝0，其两根为x 1，x 2，由题意，得⎩⎨⎧2×（－3）＝n ，－2＋5＝－m .∴m ＝－3，n ＝－6.选B. 答案 B 二、填空题6.设m ，n 分别为一元二次方程x 2＋2x －2 018＝0的两个实根，则m 2＋3m ＋n ＝________.解析 ∵m ，n 是方程x 2＋2x －2 018＝0的两根， ∴m 2＋2m －2 018＝0，即m 2＋2m ＝2 018，又m ＋n ＝－2，故m 2＋3m ＋n ＝(m 2＋2m )＋(m ＋n )＝2 018－2＝2 016. 答案 2 0167.已知方程x 2＋4x －2m ＝0的一个根α比另一个根β小4，则α＝________，β＝________，m ＝________.解析 由Δ＝16＋8m ＞0得m ＞－2，由题意α＝β－4，即α－β＝－4 ①，又α＋β＝－4 ②，由①②得α＝－4，β＝0，∴αβ＝0＝－2m ，m ＝0. 答案 －4 0 08.关于x 的一元二次方程x 2＋2x －2m ＋1＝0的两实数根为负，则实数m 的取值范围是________.解析 设方程两根为x 1，x 2，则x 1＜0，x 2＜0，∴⎩⎨⎧Δ≥0，x 1＋x 2＝－2，x 1x 2＝－2m ＋1＞0，∴0≤m ＜12. 答案 ⎣⎢⎡⎭⎪⎫0，12 三、解答题9.求下列方程的解集：(1)x 4－2x 2－8＝0；(2)6x 2－1x －1＝0.解 (1)令y ＝x 2(y ≥0)，则原方程可变为y 2－2y －8＝0，∴y ＝4或y ＝－2(舍去)，即x 2＝4，∴x ＝±2，∴原方程的解集为{2，－2}. (2)令y ＝1x ≠0，则原方程可化为6y 2－y －1＝0， ∴(3y ＋1)(2y －1)＝0， ∴y ＝－13或12，即1x ＝－13或12，∴x ＝－3或2，∴原方程的解集为{－3，2}.10.设x 1，x 2是方程3x 2－2x －4＝0的两根，不解方程，求下列各式的值； (1)1x 1＋1x 2；(2)x 2x 1＋x 1x 2；(3)(x 1－x 2)2；(4)x 31＋x 32.解由根与系数的关系，得⎩⎪⎨⎪⎧x 1＋x 2＝23，x 1x 2＝－43.(1)1x 1＋1x 2＝x 1＋x 2x 1x 2＝－12.(2)x 2x 1＋x 1x 2＝x 21＋x 22x 1x 2＝（x 1＋x 2）2－2x 1x 2x 1x 2＝（x 1＋x 2）2x 1x 2－2＝－13－2＝－73.(3)(x 1－x 2)2＝(x 1＋x 2)2－4x 1x 2＝529.(4)x 31＋x 32＝(x 1＋x 2)(x 21－x 1x 2＋x 22)＝(x 1＋x 2)[(x 1＋x 2)2－3x 1x 2] ＝(x 1＋x 2)3－3x 1x 2(x 1＋x 2)＝8027.能力提升11.已知x 1，x 2是一元二次方程(a －6)x 2＋2ax ＋a ＝0的两个实数根.(1)是否存在a ，使－x 1＋x 1x 2＝4＋x 2成立？若存在，求出a 的值；若不存在，请说明理由.(2)求使(x 1＋1)(x 2＋1)为负整数的实数a 的整数值. 解 由题意知⎩⎨⎧a －6≠0，Δ＝（2a ）2－4a （a －6）≥0，∴a ≥0且a ≠6.由根与系数的关系，得⎩⎪⎨⎪⎧x 1＋x 2＝－2aa －6，x 1x 2＝aa －6.(1)若－x 1＋x 1x 2＝4＋x 2， 则x 1＋x 2＋4＝x 1x 2， 即4－2a a －6＝aa －6，∴a ＝24. 故满足条件的a 存在，且a ＝24.(2)∵(x 1＋1)(x 2＋1)＝(x 1＋x 2)＋x 1x 2＋1＝a a －6－2aa －6＋1＝－6a －6为负整数，∴a 可取的整数为7，8，9，12.12.已知一元二次方程x 2－4x ＋k ＝0有两个不相等的实数根.(1)求k 的取值范围；(2)如果k 是符合条件的最大整数，且x 2－4x －k ＝0与x 2＋mx ＋1＝0有一个根相同，求此时m 的值.解 (1)由题意Δ＝(－4)2－4k ＝4(4－k )＞0，∴k <4.即k 的取值范围为(－∞，4).(2)∵k ∈(－∞，4)，∴k 的最大整数为k ＝3.∴方程x 2－4x －k ＝0即x 2－4x －3＝0的解集为{2－7，2＋7}.设方程x 2＋mx ＋1＝0的两根为x 1，x 2，则⎩⎨⎧x 1＋x 2＝－m ，x 1x 2＝1.若方程x 2＋mx ＋1＝0的一个根为2－7，则另一个根为12－7＝－2＋73， 此时m ＝－(x 1＋x 2)＝－⎝⎛⎭⎪⎫2－7－2＋73＝－4＋473. 若方程x 2＋mx ＋1＝0的一个根为2＋7，则另一个根为12＋7＝－2＋73， 此时m ＝－(x 1＋x 2)＝－⎝ ⎛⎭⎪⎫2＋7＋－2＋73＝－4＋473.。