中学生标准学术能力诊断性测试2019届高三11月测试 一卷数学文理2套合集含答案
- 格式:pdf
- 大小:1.21 MB
- 文档页数:15

2019届高三数学11月月考试题 理考试时间:120分钟 试卷总分:150分本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分第I 卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求,每小题选出答案后,请把答案填写在答题卡相应位置上...............。
1.若复数z 满足(3-4i )z =|4+3i |,则z 的虚部为( ) A .-4 B .-45 C .4D .452.设集合2{|20}M x x x =-≥,{|N x y ==,则M N 等于( )A .(1,0]-B .[1,0]-C .[0,1)D .[0,1] 3.已知平面向量,a b 满足()5a a b +=,且2,1a b ==,则向量a 与b 夹角的正弦值为( )A .12 B . .12-4.已知命题p :R x ∈∀,0312>+x ,命题q :“20<<x ”是“1log 2<x ”的充分不必要条件,则下列命题为真命题 的是( )A .p ⌝B .q p ∧C .)(q p ⌝∧D .()p q ⌝∨5.执行如图所示的程序框图,若输入n 的值为5,则输出S 的值为( ) A .11B .12C .9D .106.已知数列{}n a 中,()111,21,n n na a a n NS *+==+∈为其前n 项和,5S的值为( )A .57B .61C .62D .637.函数y=A sin(ωx+φ)的周期为2π,其图象的一部分如图所示,则此函数的解析式可以写成( )2)A .)x (f =sin(2—2x )B .)x (f =sin(2x 一C .)x (f =sin(x 一1)D .)x (f =sin(1一x)8.某几何体的三视图如图所示,其中俯视图为扇形, 则该几何体的体积为( ) A .23π B .3πC .29πD .169π 9.若A 为不等式组002x y y x ≤⎧⎪≥⎨⎪-≤⎩表示的平面区域,则当a 从2-连续变化到1时,动直线x y a +=扫过A 中的那部分区域的面积为( ) A .34 B .74 C .1 D .3210.在四面体S ABC -中,,2AB BC AB BC SA SC ⊥====,二面角S AC B --的余弦值是3-,则该四面体外接球的表面积是( )A. B .6π C .24π D11.已知函数()()()()()52log 11221x x f x x x -<⎧⎪=⎨--+≥⎪⎩,则关于x 的方程()()f x a a R =∈实根 个数不可能为( )A .2个B .3个C .4个D .5 个12.已知R a ∈,若()()e xaf x x x=+在区间(0,1)上有且只有一个极值点,则a 的取值 范围为( ) A .0a >B .1a ≤C .1a >D .0a ≤第II 卷(非选择题,必做部分,共80分)二、填空题 :本大题共4小题,每小题5分,共20分,请把答案填在答题卡的横线上.............。

2019年高三11月期中联考(数学文)本试卷共4页,分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题目)两部分,共150分,考试时间120分钟。
注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准备考证号、考试科目用铅笔涂写在答题卡上。
2.每题选出答案后,用2B铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再改涂在其它答案标号。
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合}3=n∈-<NnmZmBA,则<},2{|1=3∈-<|{≤A.{0,1}B.{-1,0,1}C.{0,1,2}D.{-1,0,1,2}2.下列命题中的假命题是A. B.C. D.3.已知条件,条件,则是成立的A.充分不必要条件B.必要不充分条件C.充要条件D.既非充分也非必要条件4.将函数的图象向右平移个单位,再向上平移1个单位,所得函数图象对应的解析式为A. B.C. D.5.已知,那么等于A. B. C. D.6.设等比数列中,前n项和为,已知,则A. B. C. D.7.设3.0log ,9.0,5.054121===c b a ,则的大小关系是A. B. C. D.8.函数的图象大致是9.的三个内角A ,B ,C 所对的边分别为a A b B A a c b a 3cos sin sin ,,,2=+,则A. B. C. D.10.若函数⎪⎩⎪⎨⎧<->=0),(log 0,log )(212x x x x x f ,若,则实数的取值范围是 A. B.C. D.11.已知是的一个零点,,则A. B.C. D.12.已知,把数列的各项排列成如下的三角形状,记表示第行的第个数,则=A. B. C. D.第Ⅱ卷 (非选择题 共90分)二、填空题:本大题共4个小题,每小题4分,共16分。
13.若角满足,则的取值范围是 .14.若实数满足⎪⎩⎪⎨⎧≤≥+≥+-,0,0,01x y x y x ,则的值域是 .15.已知奇函数满足,且当时,,则的值为16.已知函数的定义域[-1,5],部分对应值如表,的导函数的图象如图所示,x-1 0 2 4 5 F(x) 1 2 1.5 2 1下列关于函数的命题;①函数的值域为[1,2];②函数在[0,2]上是减函数③如果当时,的最大值是2,那么t 的最大值为4;④当时,函数最多有4个零点.其中正确命题的序号是 .三、解答题:本大题共6小题,共74分。

一、单选题二、多选题1. 已知,其中,若对任意的实数b ,c 都有不等式成立,则方程的根的可能性为( )A .有一个实数根B .两个不相等的实数根C .至少一个负实数根D .没有正实数根2.若函数,则下列说法正确的是( )A.若,则对于任意函数都有2个零点B .若,则对于任意 函数 都有4个零点C .若,则存在 使得函数 有2个零点D .若,则存在 使得函数有2个零点3. 2020年第三届中国国际进口博览会开幕,时值初冬呼吸系统传染病高发期,防疫检测由上海交通大学附属瑞金医院与上海联通公司合作研发的“5G 发热门诊智慧解决方案”完成.该方案基于5G 网络技术实现了患者体温检测、人证核验、导诊、诊疗、药品与标本配送的无人化和智能化.5G 技术中数学原理之一就是香农公式:.它表示:在受噪声干扰的信道中,最大信息传递速度(单位:)取决于信道带宽(单位:)、信道内信号的平均功率(单位:)、信道内部的高斯噪声功率(单位:)的大小,其中叫做信噪比.按照香农公式,若不改变带宽,而将信噪比从1000提升至2000,则大约是原来的( )A .2倍B .1.1倍C .0.9倍D .0.5倍4. 已知是三个不同的平面,是两条不同的直线,下列命题为真命题的是( )A .若,,则B .若,,则C .若,则D .若,则5. 已知, 设集合,,则( )A.B.C .D .6. F 1、F 2分别是双曲线-=1(a >0,b >0)的左、右焦点,过点F 1的直线l与双曲线的左右两支分别交于A 、B 两点,若△ABF 2是等边三角形,则该双曲线的离心率为( )A.B.C.D.7. 已知定义域为的偶函数满足,若对任意的,且,恒成立,则不等式的解集为( )A.B.C.D.8. 在平面直角坐标系中,将点绕原点逆时针旋转到点,设直线与轴正半轴所成的最小正角为,则等于A.B.C.D.9. 近年来,中国电影行业发展迅猛,消费者追求电影剧情的高质量,重视电影内容正面传达的积极情绪,并且愿意为其买单.某机构调查到观众在观看电影时除了关注电影的剧情、情节外,还会关注电影的幕后团队、精神内涵价值观、参演人员等方面.如图所示为该机构调查的2023年中国网民观看电影时关注方面占比的统计表,则下列结论正确的是( )中学生标准学术能力诊断性测试(THUSSAT)2023-2024学年高三上学期11月测试数学试卷中学生标准学术能力诊断性测试(THUSSAT)2023-2024学年高三上学期11月测试数学试卷三、填空题四、解答题A .2023年中国网民观看电影时超过40%的网民会关注参演人员B .这8个方面占比的极差是31.77%C .这8个方面占比的中位数为37.69%D .2023年中国网民观看电影时至少有10.73%的网民既关注剧情、情节,又关注精神内涵价值观10.如图,已知是边长为4的等边三角形,D ,E 分别是AB ,AC 的中点,将沿着DE 翻折,使点A 到点P处,得到四棱锥,则()A .翻折过程中,该四棱锥的体积有最大值为3B.存在某个点位置,满足平面平面C .当时,直线与平面所成角的正弦值为D .当时,该四棱锥的五个顶点所在球的表面积为11.已知等差数列的前n 项和为,等比数列的前n项和为,则下列说法正确的是( )A .若,则B.,,成等差数列C.,,成等比数列D .若,,则使得取得最大值的正整数n 的值为812. 关于函数,,下列说法正确的是( )A .当时,在处的切线方程为B .当时,存在唯一极小值点且C .对任意,在上均存在零点D .存在,在上有且只有一个零点13.由曲线 ,,形成的封闭图形绕y 轴旋转一周所得的旋转体的体积为V ,则V =__________.14.已知数列的通项公式,其前n 项和为,则_____.(用分数作答)15. 设函数的图象过点A (2,1),且在点A 处的切线方程为,则________.16. 已知函数.(1)求在点处的切线方程,并证明;(2)若方程有两个正实数根,求证:.17.已知函数的图象经过点(1)求;(2)在中,A、B、C的对边为a、b、c,a=,,角C为锐角且,求c边长.18. 设等差数列的前项和为,且,.(1)求数列的通项公式;(2)设数列满足,求的前项和.19. 在中,设角A,B,C的对边分别为a,b,c,且满足.(1)求角B的大小;(2)求的取值范围.20. 魔方,又叫鲁比克方块,最早是由匈牙利布达佩斯建筑学院厄尔诺·鲁比克教授于1974年发明的.魔方与华容道、独立钻石棋一起被国外智力专家并称为智力游戏界的三大不可思议,而魔方受欢迎的程度更是智力游戏界的奇迹.通常意义下的魔方,即指三阶魔方,为的正方体结构,由个色块组成.常规竞速玩法是将魔方打乱,然后在最短的时间内复原.截至2020年,三阶魔方还原官方世界纪录是由中国的杜宇生在2018年11月24日于芜湖赛打破的纪录,单次秒.(1)某魔方爱好者进行一段时间的魔方还原训练,每天魔方还原的平均速度(秒)与训练天数(天)有关,经统计得到如下数据:(天)(秒)现用作为回归方程类型,请利用表中数据,求出该回归方程,并预测该魔方爱好者经过长期训练后最终每天魔方还原的平均速度约为多少秒(精确到)?参考数据(其中)(2)现有一个复原好的三阶魔方,白面朝上,只可以扭动最外侧的六个表面.某人按规定将魔方随机扭动两次,每次均顺时针转动,记顶面白色色块的个数为,求的分布列及数学期望.21. 如图,据气象部门预报,在距离某码头南偏东45°方向600km处的热带风暴中心正以20km/h的速度向正北方向移动,距风暴中心450km以内的地区都将受到影响.据以上预报估计,从码头现在起多长时间后,该码头将受到热带风暴的影响,影响时间大约为多长(精确到0.1h)?。

山东省曲阜夫子学校2019届高三数学上学期11月质量检测试题理本试卷分第I卷和第Ⅱ卷两部分,共4页,满分150分.考试用时120分钟,考试结束后,将本试卷和答题卡一并交回.第I卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.每小题给出的四个选项中只有一项是符合题目要求的.(1)复数(是虚数单位)的共轭复数表示的点在()(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限(2)集合,,则( )(A)(B)(C)(D)(3)设M是边BC上任意一点,N为AM的中点,若,则的值为( )(A)(B)(C)(D)1(4)设均为单位向量,则“”是“”的()(A)充分而不必要条件(B)必要而不充分条件(C)充分必要条件(D)既不充分也不必要条件(5)设,,,则()(A) (B) (C) (D)(6)把函数的,图象上各点的横坐标伸长到原来的2倍,再把所得图象向右平移个单位则所得图象对应的函数解析式是()(A) (B)(C) (D)(7)在中,角均为锐角,且,则的形状是()(A)直角三角形(B)锐角三角形(C)钝角三角形(D)等腰三角形(8)已知函数,且实数满足,若实数是函数=的一个零点,那么下列不等式中不可能...成立的是()(A) (B)(C)(D)(9)若函数在区间上的值域为,则的值是()(A)0 (B) 2 (C)4 (D)6(10)《数书九章》中对已知三角形三边长求三角形的面积的求法填补了我国传统数学的一个空白,与著名的海伦公式完全等价,由此可以看出我国古代已具有很高的数学水平,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实.一为从隅,开平方得积.”若把以上这段文字写成公式,即.现有周长为的满足,试用以上给出的公式求得的面积为()(A)(B)(C)(D)(11)已知函数与的图象上存在关于轴对称的点,则的取值范围是()(A)(B)(C)(D)(12)设,若函数在区间上有三个零点,则实数的取值范围是 ( )(A)(B)(C)(D)第II卷(共90分)二、填空题:本大题共4个小题,每小题5分,共20分.(13)已知为等差数列,++=2019,=2013,以表示的前项和,则使得达到最大值的是__________.(14)设函数f(x)=,若对任意的实数x都成立,则ω的最小值为__________.(15)已知定义在R上的奇函数,满足,且在区间[0,1]上是增函数,若方程在区间上有四个不同的根,则(16)已知,,分别是的两个实数根,则__________.三、解答题:本大题共6小题,共70分,解答应写出必要的文字说明,证明过程或演算步骤.(17)(本小题满分10分)设命题:函数的定义域为;命题:不等式对一切正实数均成立. (Ⅰ)如果是真命题,求实数的取值范围;(Ⅱ)如果命题“或”为真命题,且“且”为假命题,求实数的取值范围.(18)(本小题满分12分)已知向量−,1),,),函数.(Ⅰ)求函数的单调递增区间;(Ⅱ)若,,分别是角,,的的对边,,,且=1,求△的面积.(19)(本小题满分12分)在△中,,,分别是角,,的对边,,且.(Ⅰ)求角;(Ⅱ)求边长的最小值.(20)(本小题满分12分)(本小题满分12分)已知为等比数列,其中,且成等差数列.(Ⅰ)求数列的通项公式;(Ⅱ)设,求数列的前n项和为.(21)(本小题满分12分)已知.(Ⅰ)当时,求的极值;(Ⅱ)若有2个不同零点,求的取值范围.(22)(本小题满分12分)已知函数.(Ⅰ)求函数的单调增区间;(Ⅱ)记函数的图象为曲线,设点是曲线上两个不同点,如果曲线上存在点,使得:①;②曲线在点处的切线平行于直线,则称函数存在“中值相依切线”.试问:函数是否存在中值相依切线,请说明理由.理科数学参考答案一、选择题(1)B (2) A (3)A (4)C (5) B (6) D (7) C (8)D (9)B (10)C (11) B (12)D(1)【解析】因为,所以表示的点在第二象限,故选B.(2),,故选D.故选B.(10)【解析】因为,所以由正弦定理得,又,所以,,,则,,故.故选C.二、填空题:(13)350 (14)(15)(16)三、解答题(17)解:(I)若命题为真,即恒成立①当时,不合题意…………………………………………………1分②当时,可得,即………………………5分(II)令由得若命题为真,则………………………………………………………………6分由命题“或”为真且“且”为假,得命题、一真一假……………7分①当真假时,不存在②当假真时,…………………………………………………………10分(18)解:(Ⅰ)=m·n=−+=………………………………3分由,k∈Z,得,k∈Z,故函数的单调递增区间为[kπ−,kπ+](k∈Z).………………………………5分(2)由题意得=sin(2A−)=1,∵A(0,π),∴2A−,错误!未找到引用源。

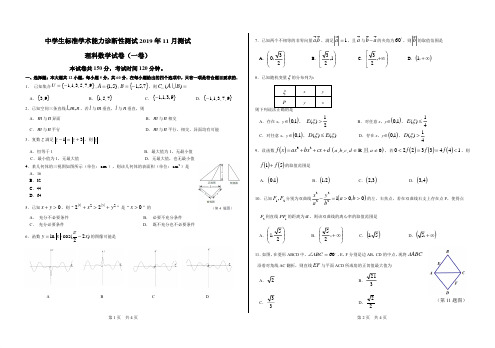
中学生标准学术能力诊断性测试2019年11月测试理科数学试卷(一卷)本试卷共150分,考试时间120分钟。
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知集合{}1,1,3,5,7,9U =−,{1,5}A =,{}7,5,1−=B ,则()U C A B =A .{}3,9 B .{}1,5,7 C .{}1,1,3,9− D .{}1,1,3,7,9−2.已知空间三条直线n m l ,,,若l 与m 垂直,l 与n 垂直,则A .m 与n 异面B .m 与n 相交C .m 与n 平行D .m 与n 平行、相交、异面均有可能 3.复数z 满足31+=−z z ,则zA .恒等于1B .最大值为1,无最小值C .最小值为1,无最大值D .无最大值,也无最小值 4.某几何体的三视图如图所示(单位:cm ),则该几何体的表面积(单位:2cm )是 A .16 B .32 C .44D .64 5.已知0>+y x ,则“2||2||22y x y x +>+”是“0>x ”的A . 充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分也不必要条件 6.函数ln cos(2)2y x x π=⋅−的图像可能是A B C D7.已知两个不相等的非零向量b ,a ,满足1=a ,且a 与a b −的夹角为 60,则b的取值范围是A .⎪⎪⎭⎫ ⎝⎛230,B .⎪⎪⎭⎫⎢⎣⎡1,23C .⎪⎪⎭⎫⎢⎣⎡+∞,23 D .()∞+,1 8.已知随机变量ξ的分布列为:ξx y Pyx则下列说法正确的是 A .存在x ,y ()1,0∈,1()2E ξ>B .对任意x ,y ()1,0∈,1()4E ξ≤C .对任意x ,y ()1,0∈,()()DE ξξ≤ D .存在x ,y ()1,0∈,1()4D ξ>9.设函数()d cx bx ax x f +++=23(),,,0a b c d a ∈≠R 且,若()()()14433220<==<f f f ,则()()51f f +的取值范围是A .()10, B .()21,C .()3,2D .()4,3 10.已知21,F F 分别为双曲线()0012222>>=−,b a by a x 的左、右焦点,若在双曲线右支上存在点P ,使得点2F 到直线1PF 的距离为a ,则该双曲线的离心率的取值范围是A .⎪⎪⎭⎫⎝⎛251, B .⎪⎪⎭⎫ ⎝⎛∞+,25 C .()51, D .()∞+,511.如图,在菱形ABCD 中,60ABC∠=,E ,F 分别是边AB ,CD 的中点,现将ΔABC沿着对角线AC 翻折,则直线EF 与平面ACD 所成角的正切值最大值为A .2 B .321C .33 D .22(第11题图)12.已知数列}{n a 满足11=a ,11ln 1++=+nn n a a a ,记[][][]n n a a a S +++= 21,[]t 表示不超过t 的最大整数,则2019S 的值为A .2019B .2018C .4038D .4037 二、填空题:本大题共4小题,每小题5分,共20分. 13.在[]2,2−上随机地取一个实数k ,则事件“直线kx y =与圆()9522=+−y x 相交”发生的概率为 .14.如图,在ABC ∆中,AC AB >,32=BC ,︒=60A ,ABC ∆的面积等于32,则角平分线AD 的长等于 .15.已知数列}{n a 满足n a a n n 2151−=++,其前n 项和为n S ,若n S 8S ≤恒成立,则1a 的取值范围为 .16.已知P 为椭圆C :22+143x y =上一个动点,1F 、2F 是椭圆C 的左、右焦点,O 为坐标原点,O 到椭圆C 在P 点处的切线距离为d ,若12247PF PF ⋅=,则d = . 三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:60分. 17.(12分)已知函数x x x f cos 3sin )(−=(1)求函数()f x 的单调递增区间;(2)在ABC ∆中,角,,A B C 所对的边分别是a ,b ,c ,若()3f B =,3b =,求ABC∆面积的最大值.18.(12分)如图,已知四棱锥P —ABCD 中,底面ABCD 是直角梯形,AD //BC ,BC =2AD ,AD ⊥CD ,PD ⊥平面ABCD ,E 为PB 的中点. (1)求证:AE //平面PDC ;(2)若BC =CD =PD ,求直线AC 与平面PBC 所成角的余弦值.19.(12分) 已知甲盒内有大小相同的2个红球和3个黑球,乙盒内有大小相同的3个红球和3个黑球,现从甲,乙两个盒内各任取2个球.(1)求取出的4个球中恰有1个红球的概率;(2)设ξ为取出的4个球中红球的个数,求ξ的分布列和数学期望.20.(12分)如图,斜率为k 的直线l 与抛物线24y x =交于A 、B 两点,直线PM 垂直平分弦AB ,且分别交AB 、x 轴于M 、P ,已知()4,0P . (1)求M 点的横坐标;(2)求PAB △面积的最大值.21.(12分)已知函数xaxx x f −=ln )(,R a ∈. (1)若函数)(x f 有且只有两个零点,求实数a 的取值范围;(2)设函数)(x f 的两个零点为21,x x ,且21x x ≠,求证e x x 221>+.(二)选考题:共10分.请考生在第22,23题中任选一题作答,如果多做,则按所做的第一题计分.作答时请写清题号.22.[选修4—4:坐标系与参数方程](10分) 在平面直角坐标系xOy 中,曲线C 的参数方程为4cos 2sin x y αα=⎧⎨=⎩(α为参数),在以坐标原点O 为极点,x 轴的正半轴为极轴的极坐标系中,点P 的极坐标为4,3π⎛⎫ ⎪⎝⎭,直线l 的极坐标方程为2sin 96ρθπ⎛⎫−= ⎪⎝⎭. (1)求直线l 的直角坐标方程与曲线C 的普通方程;(2)若Q 是曲线C 上的动点,M 为线段PQ 的中点,直线l 上有两点A,B ,始终满足AB 4=,求MAB △面积的最大值与最小值.23.[选修4—5:不等式选讲](10分)已知c b a ,,为正实数,且满足3=++c b a .证明:(1)3≤++ac bc ab ; (2)3222≥++ac c b b a .(第14题图)l中学生标准学术能力测试诊断性测试2019年11月测试理科数学(一卷)答案一. 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只二. 填空题:本大题共4小题,每小题5分,共20分. 13.3814.315. (,7]−∞16.2三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:60分.17.解:()sin 2sin()3f x x x x π==− ………………………………2分(1)令22232k x k πππππ−≤−≤+(k Z ∈)得52266k x k ππππ−≤≤+(k Z ∈) 故函数()f x 的单调递增区间为52,266k k ππππ⎡⎤−+⎢⎥⎣⎦(k Z ∈) …………………5分(2)由()f B = ,得sin()3B π−=323πππ+=−k B 或,3223πππ+=−k B∴222,3B k B k k Z ππππ=+=+∈或 ,32π=∴B B 是三角形的内角, . ………………………………7分∵B ac c a b cos 2222−+= ∴922=++ac c a∴92≤+ac ac ,即3≤ac ………………………………9分 ∴133sin 24ABC S ac B ∆=≤. ………………………………11分 当且仅当3a c == 时,ABC ∆面积的最大值是334. ……………………………12分 18.(1)取PC 的中点F ,连接DF ,EF , ∵ E 是PB 的中点, ∴ EF //BC ,且BC =2EF , 又 AD //BC ,BC =2AD∴ AD //EF 且AD =EF , ………………………………2分 ∴ 四边形ADFE 是平行四边形,∴ AE //DF ,又DF ⊂平面PDC ,AE PCD ⊄平面 , ……………………………… 4分 ∴ AE //平面PDC . ………………………………5分 (2)若PD =DC ,则△PDC 是等腰三角形, ∴ DF ⊥PC ,又AE //DF ,∴ AE ⊥PC∵ PD ⊥平面ABCD ,BC ⊂平面ABCD ∴ PD ⊥BC , 又 BC ⊥CD ,CDPD D = ∴ BC ⊥平面PDC , ………………………………7分 ∵ DF ⊂平面PDC ∴ BC ⊥DF ∴ BC ⊥AE 又 AE ⊥PC ,PCBC C =∴ AE ⊥平面PBC , ………………………………9分 连接EC ,AC ,则∠ACE 就是直线AC 与平面PBC 所成的角. ………………………10分 设PD =CD =BC =2,EBAPCD F在Rt △PCB 中,求得PC=,PB= ,EC在Rt △ADC 中,求得AC∴ 在Rt △AEC中,c s o EC ECA AC ==∠. ………………………………12分19.(1)设事件i A 为“甲盒中取出i 个红球”,事件j B 为“乙盒中取出j 个红球”则()()2223332256,i ij ji j C C C C P A P B C C −−== 设事件C 为“4个球中恰有1个红球”()()()021111022333233301102222565639633C 1015101510C C C C C C C C P P A B P A B C C C C ∴=+=⋅+⋅=⋅+⋅=…………………………………3分(2)ξ可取的值为0,1,2,34,()()02022333002256C C C C 30B =C C 50P P A ξ∴===⋅ ……5分 ()()31C 10P P ξ===()()()()022011112002233323332333021120222222565656112++25C C C C C C C C C C C C P P A B P A B P A B C C C C C C ξ==+=⋅+⋅⋅=………………………………7分()()()112020112333233312212222565693++50C C C C C C C C P P A B P A B C C C C ξ===⋅⋅= …………………9分()()20202333222256C C C C 14B =C C 50P P A ξ∴===⋅ ………………………………10分的分布列为:33119190123+450102550505E ξ∴=⨯+⨯+⨯+⨯⨯= ………………………………12分20.(1)设112200(,),(,),(,)A x y B x y M x y ,则121200,22x x y y x y ++==,……1分 ∴ 121212042y y k x x y y y −===−+ , ………………………………3分而004MP y k x =−, ………………………………4分 由1MP k k ⋅=− 得042x −=− ,即02x =. ………………………………5分(2)设直线0:()2AB x m y y =−+ 即0:2AB x my my =−+ , 与抛物线24y x = 联立得204480y my my −+−= ,220164(48)0,2m my m =−−>∴<△则121204,48y y m y y my +==−, ………………………………7分所以12|||AB y y =−=, 而P 到直线AB的距离为d =所以01||2|22PAB S d AB my ∆==+ ………………………………9分 又由于012y m k ==,所以222(24(PAB S m m ∆=+=+(22m <), …………………10分t =,则0t >且222m t =−, 所以234(3)124PAB S t t t t ∆=−=− , 令3()124(0)g t t t t =−> ,则2()121212(1)(1)g t t t t '=−=−+,当01t << ,()0g t '> ,当1t >时,()0g t '<,故3()124(1)8g t t t g =−≤=,即PAB ∆面积的最大值为8. ………………………12分21.(1)解:21ln ')0,xf x x e x−==∴=( 当')00,()0)f x x e f x e ><<∴(时,在(,上单调递增 , 当')0,(),)f x x e f x e <>∴+∞(时,在(上单调递减. 1)()f x f e a e∴==−极大值( ……3分,1)0f x a e∴<<(有且只有两个零点,,00()0x x f x >→<又且时,0()0x a f x →+∞=>时,若时,不符合题意,0lim ()0x a f x a →+∞<=−>若时,不符合,0lim ()0x a f x a →+∞>=−<若时,满足,综上,若使()f x 有且只有两个零点,10a e∴<< …………………… 4分 (2)证法一:ln ln )0ln ,ln x xf x a x ax x a e x=−=∴=∴=⋅(,,12ln ,ln x x x xe a −∴=是的两根 tt e t t g e t t g x t x t −−−=⋅===)1()(',)(,ln ,ln 2211设,上单调递减上单调递增,在,在(),1[]1-)(+∞∞∴t g , ………………………………6分,10,),()(212121t t t t t g t g <<<<=则必有设 ),(构造函数10),1()1()(G ∈−−+=t t g t g t ,,01-()1(')1(')(G'21>=−++=+)tt e ett g t g t,0)0()(,)1,0()(G =>∴∈∴G t G t t 上单调递增在 ………………………………9分)()()2(211t g t g t g =>−∴,上单调递减,在又),1()(),,1(,221+∞∈+∞∈−t t g t t 2,-22121>+∴<∴t t t t ,12ln ln 2x x ∴+>,即212x x e ⋅>;122x x e +∴>>,即122x x e +>.……12分 证法二:不妨设121x e x <<<,)()(21x f x f = ,1212ln ln x x x x ∴=,即2211ln ln x x x x ∴=, ………………………………6分设21(1)x tx t => ,1111ln ln ln ln ln tx t x t x x +∴==,1ln ln 1t x t ∴=−, 1ln 1ln ln ln ln )ln(ln 112−=−+=+==t t t t t t x t tx x ,t t t x x ln 11ln ln 21⋅−+=+∴,122x x +> ,要证122x x e +>,只需证212x x e ⋅>, 即证121ln ln ln 21t x x t t ++=⋅>− ,即证2(1)ln 01t t t −−>+. …………………………9分 设2(1)()ln ,(1)1t g t t t t −=−>+, 22214(1)'()0(1)(1)t g t t t t t −=−=>++,()g t ∴在(1,)+∞单调递增. 0)1(=g ,0)1()(=>∴g t g ,12ln ln 2x x ∴+>,122x x e +∴>>,即122x x e +>.………………………12分 证法三:不妨设121x e x <<<,12()()f x f x =,1212ln ln x x x x ∴=, ………………………………6分 要证122x x e +>,只需证122112112ln ln ln x x x x xe x x x +−>=>− , ……………………7分 变形,得:2121212()ln ln x x x x x x −−>+,即2212112(1)ln 1x x x x x x −>+.设212(1)ln (1)1x t t t t x t −=∴>>+ ,设2(1)()ln ,(1)1t g t t t t −=−>+,……………………10分 22214(1)'()0(1)(1)t g t t t t t −=−=>++,()1g t ∴+∞在(,)上单调递增, ()(1)0g t g ∴>=,12112ln x x xe x +∴>=成立,122x x e ∴+>.………………………12分(二)选考题:共10分.请考生在第22,23题中任选一题作答,如果多做,则按所做的第一题计分.作答时请写清题号. 22.【选修4−4:坐标系与参数方程】(10分) (1)因为直线l 的极坐标方程为2sin 96ρθπ⎛⎫−= ⎪⎝⎭,即12sin cos 922ρθθ⎛⎫−⋅= ⎪ ⎪⎝⎭.由cos ,sin x y ρθρθ==,可得直线l 的直角坐标方程为90x +=. ………………………………2分将曲线C 的参数方程4cos 2sin x y αα=⎧⎨=⎩,消去参数a ,得曲线C 的普通方程为224161x y +=. ………………………………4分(2)设()Q 4cos ,2sin αα ,[)0,2απ∈ .点P 的极坐标4,3π⎛⎫⎪⎝⎭,化为直角坐标为(2, .则(M 2cos +1,sin αα+. ………………………………6分所以点M 到直线l 的距离d ==,(其中,tan θ=),所以77d 22⎡+∈⎢⎣⎦ ………………………………8分AB 4= ,12772ΔMAB S AB d d ⎡∴=⋅=∈−⎣ ∴MAB △面积的最大值为77+,最小值为77− …………………………10分23.【选修4−5:不等式选讲】(10分)23.(1)因为,,a b c 为正实数,且满足3a b c ++=.所以,()bc ac ab c b a c b a 2222222+++++=++ac c bc,a c ab,b b a 222222222≥+≥+≥+ ,ac bc ab c b a ++≥++∴222 ……2分()2333a b c ab ac bc ∴++≥++ ,3a b c ++=,∴3ab bc ac ++≤,当且仅当a b c ==时,等号成立 ………………………………5分(2)2222,2,2a b c b a c b a c b c a+≥+≥+≥ , ()2222a b c a b c a b c b c a ∴+++++≥++ ………………………………8分222a b c a b c b c a ∴++≥++ ,3a b c ++= ,2223a b c b c a∴++≥ ,当且仅当a b c == 时,等号成立 ………………………………10分。
2019-2020年高三11月模块学业水平检测数学(文)试题含答案注意事项:1.样题分第Ⅰ卷、答题纸,满分150分,考试时间120分钟;考试结束,将答题纸和答题卡一并上交。
2.答第Ⅰ卷前,考生务必将自己的准考证号、考试科目、试卷类型,用2B铅笔写在答题卡上,用0.5mm的黑色签字笔填写姓名。
3.选择题每题选出答案后都必须用2B铅笔把答题卡上对应题目的答案标号(A、B、C、D)涂黑,如需改动,必须先用橡皮擦干净,再选涂其它答案,不能答在试卷上。
4.填空题、解答题按要求答在答题纸上。
使用答题纸时:①必须使用0.5mm的黑色签字笔书写,字体工整,笔迹清楚,使用2B铅笔画图。
②必须按照题号顺序在各题目的相应答题区域内作答,不按题号顺序答题或超出答题区域书写的答案无效。
严禁使用涂改液、胶带纸、修正液。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合,则“”是“”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.若复数为纯虚数,则实数的值为A. B. C. D.或3.函数的定义域是A.B.C.D.4. 函数是A. 最小正周期为的偶函数,最大值为B. 最小正周期为的奇函数,最大值为C. 最小正周期为的偶函数,最大值为D. 最小正周期为的奇函数,最大值为5.函数的图象大致是A.B.C.D.6.某商场在庆“十一”的促销活动中,对时至时的销售额进行统计,其频率分布直方图如图所示.已知时至时的销售额为万元,则时至时的销售额为A.万元B.万元C.万元D.万元7.已知满足不等式组,则的最大值为A.B.C.D.8.执行右图的程序框图,若输出的,则输入整数的最大值是A.B.C.D.9.若,则下列结论正确的是A.B.C.D.10.数列中,已知对任意,,则…等于A. B. C. D.11.函数的定义域为,若对于任意,当时都有,则称函数在上为非减函数.设函数在上为非减函数,且满足以下三个条件:①;②;③,则等于A. B.C.D.12.函数,.实数满足,,则A.B.C.D.二、填空题:本大题共4个小题,每小题4分,满分16分.13.已知函数,则________.14.某高中为调查了解学生体能状况,按年级采用分层抽样的方法从所有学生中抽取人进行体育达标测试.该校高二年级共有学生人,高一、高二、高三三个年级的人数依次成等差数列.若从高一年级中抽取了人,则从高三年级中抽取了_______人.15.已知,,则________.16.已知函数,定义在R上的奇函数满足,当时,,则集合等于________.三、解答题:本大题共6个小题,共74分。
中学生标准学术能力诊断性测试 2018 年 11 月测试理科综合试卷(一卷)本试卷共 300 分,考试时间 150 分钟。
可能用到的相对原子质量:锆(Zr )-91 Cl-35.5 O-16 Si-28 Ge-73一、选择题:本题共 13 小题,每小题 6 分,共 78 分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.关于细胞内所含有的“骨架”说法错误的是: A .“细胞的蓝图—DNA”的骨架是磷酸和脱氧核糖交替连接构成的 B .多糖、蛋白质、核酸等生物大分子都以碳链为骨架C .单糖、氨基酸、核苷酸等单体也以若干个相连的碳原子构成的碳链为基本骨架D .真核细胞中维持细胞形态的细胞骨架是由蛋白质和磷脂构成的网架结构2.右图是物质进出细胞的运输方式示意图,以下有关说法正确的是:A .胰岛素通过丁图所示过程进入细胞发挥作用B .通过丙图出细胞的物质并不一定是大分子C .甲图所示跨膜方式使膜两侧离子趋于平衡D .乙图所示过程与小肠绒毛上皮细胞吸收葡萄糖的方式相同3.自 2017 年 7 月以来,宫颈癌疫苗(HPV 疫苗)在国内得到推广。
该疫苗是 HPV (DNA 病毒,宿主细胞为上皮细胞)灭活纯化制备,接种三针可预防宫颈癌症的发生,下列说法错误的是: A .HPV 的核酸彻底水解后可以获得 6 种化合物B .若想用 32P 标记 DNA 可把 HPV 培养在含 32P 的磷酸盐溶液里C .若想验证 HPV 遗传物质是 DNA ,可用含有同位素标记的 T 或 U 的上皮细胞来培养病毒,观察其子代病毒的放射性D .HPV 侵入人体后,大多数情况下人体可以通过体液免疫和细胞免疫来清除病毒4.美国生物学家发现 1-甲基环丙烯(1-MCP )可作为保鲜剂用于储存果蔬。
科学家用适宜浓度 1-MCP 对柿子果实的细胞呼吸速率和乙烯产生量的影响进行了研究,结果如图。
请据图选出错误的是:A .由图甲可推测,1-MCP 可能抑制呼吸酶来减弱细胞呼吸延迟呼吸高峰的到来,从而对果蔬进行保鲜,降低果蔬营养物质的损耗B .由图乙可推测,1-MCP 是通过抑制乙烯的产生延长了果蔬的储运期C .研究发现柿子细胞表面乙烯受体数量正常,1-MCP 可能优先结合乙烯受体,抑制果蔬对乙烯的反应,延缓果蔬成熟D .农业生产上可在一开始坐果时立即使用 1-MCP ,使果实延迟成熟上市5.生态果园是利用生态工程学原理,科学配置各成分及资源而建立的可持续发展的果园生产体系。
2019届高三11月联考试卷数学(文)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合,则()A. B. C. D.【答案】D【解析】由题意知,,所以,故选D.2. 设命题,则是()A. B. C. D.【答案】D所以:,故选D.3. 已知向量.若,则实数()A. B. C. D.【答案】B【解析】由题意知,,因为,所以,解得,故选B.4. “”是“”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件【答案】A【解析】当时,;当时,或,即或,所以“”是“”的充分不必要条件,故选A.5. 设是自然对数的底数,函数是周期为4的奇函数,且当时,,则的值为()A. B. C. D.【答案】D【解析】因为,所以,故选D.6. 某县2015年12月末人口总数为57万,从2016年元月1日全面实施二胎政策后,人口总数每月按相同数目增加,到2016年12月末为止人口总数为57.24万,则2016年10 月末的人口总数为()A. 57.1万B. 57.2万C. 57.22万D. 57.23万【答案】B【解析】由题意知,人口总数可以看成是一个以为首项,为公差的等差数列,则,则由,得,解得,于是年月末的人口总数是,故选B.7. 在中,角的对边分别为,,则()A. 1B. 2C. 3D. 4【答案】C【解析】因为,所以,又,即,解得,故选C.8. 设等比数列的前项和为,且,则首项()A. 3B. 2C. 1D.【答案】C【解析】设数列的公比为,显然,则,两式相除,得,解得,所以,故选C.9. 若正数满足,则()A. 有最小值36,无最大值B. 有最大值36,无最小值C. 有最小值6,无最大值D. 有最大值6,无最小值【答案】A【解析】因为,所以,因为,所以,解得,即,则的最小值为,无最大值,故选A.10. 已知函数的部分图象如图所示,其中分别是函数的图象的一个最低点和一个最高点,则()A. B. C. D.【答案】A【解析】由题意知,,所以,所以,所以,所以,解得,因为,所以,所以,故选A.11. 如图,在四边形中,已知,,则()A. 64B. 42C. 36D. 28【答案】C【解析】由,解得,同理,故选C.点睛:本题主要考查了平面的运算问题,其中解答中涉及到平面向量的三角形法则,平面向量的数量积的运算公式,平面向量的基本定理等知识点的综合考查,解答中熟记平面的数量积的运算和平面向量的化简是解答的关键,试题比较基础,属于基础题.12. 若函数有4个零点,则实数的取值范围是()A. B. C. D.【答案】B【解析】当时,恒成立,又,则函数在上有且只有1个零点;当时,函数,则函数在上单调递增,在上单调递减,在上单调递增,所以此时函数的极大值为,极小值为,要使得有4个零点,则,解得,故选B.点睛:本题主要考查了根据函数的零点求解参数的取值范围问题,其中解答中涉及到利用导数研究函数的单调性,利用导数研究函数的极值等知识点的综合应用,着重考查了数形结合思想和转化与化归思想的应用,解答中把函数的零点问题转化为函数的图象与的交点个数,利用函数的极值求解是解答的关键,试题有一定的难度,属于中档试题.二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 已知函数的图象在点处的切线斜率是1,则此切线方程是__________.【答案】【解析】因为,所以,所以,所以,所以,则所求切线的方程为,即.14. 设变量满足约束条件,则的最小值是__________.【答案】【解析】作出不等式组所表示的可行域,如图所示,其中,作出直线,平移直线,当其经过点时,取得最小值,此时.15. 在数列中,,.记是数列的前项和,则的值为__________.【答案】130【解析】由题意知,当为奇数时,,又,所以数列中的偶数项是以为首项,为公差的等差数列,所以;当为偶数时,,又,所以数列中的相邻的两个奇数项之和均等于,所以,所以.点睛:本题主要考查了数列求和问题,其中解答中涉及到等差数列的判定、等差数列的前项和公式,以及数列的并项求和等知识点的综合应用,解答中根据题意,合理根据为奇数和为偶数分成两个数列求解是解答的关键,着重考查了学生分析问题和解答问题的能力,试题有一定的难度,属于中档试题.16. 达喀尔拉力赛(The Paris Dakar Rally )被称为世界上最严酷、最富有冒险精神的赛车运动,受到全球五亿人以上的热切关注.在如图所示的平面四边形中,现有一辆比赛用车从地以的速度向地直线行驶,其中,,.行驶1小时后,由于受到沙尘暴的影响,该车决定立即向地直线行驶,则此时该车与地的距离是__________.(用含的式子表示)【答案】【解析】假设过了小时后,到达,则,连接,在中,,所以,所以,所以,在中,,所以,则,所以.点睛:本题主要考查解三角形的实际应用问题,其中解答中涉及到正弦定理和余弦定理,以及直角三角形中的勾股定理的应用,着重考查了学生分析问题和解答问题的能力,此类问题的解答中合理选择三角形,在三角形中正确应用正、余弦定理是解答的关键,试题有一定的难度,属于中档试题.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 设,已知命题函数有零点;命题,.(1)当时,判断命题的真假;(2)若为假命题,求的取值范围.【答案】(1)真命题;(2)【解析】试题分析:(1)当时,可得在上恒成立,即可得到命题的真假;(2)由为假命题,则都是假命题,进而可求解的取值范围.试题解析:(1)当时,,在上恒成立,∴命题为真命题.(2)若为假命题,则都是假命题,当为假命题时,,解得;当为真命题时,,即,解得或,由此得到,当为假命题时,,∴的取值范围是.18. 设向量,其中,且函数.(1)求的最小正周期;(2)设函数,求在上的零点.【答案】(1);(2)和【解析】试题分析:(1)由题意,可化简得,即可计算函数的最小正周期;..................试题解析:(1),∴函数的最小正周期为.(2)由题意知,,由得,,当时,,∴或,即或.∴函数在上的零点是和.19. 已知数列满足:.(1)证明:数列是等比数列;(2)设,求数列的前项和.【答案】(1)见解析;(2)【解析】试题分析:(1)根据题意,可化简得,即可得到数列是以为首项,为公比的等比数列. (2)由(1)知,求得,再利用乘公比错位相减法,即可求解数列的前项和.试题解析:(1)∵,∴,∴,则数列是以1为首项,2为公比的等比数列. (2)由(1)知,,∴,∴.∴,,∴,∴.20. 设函数.(1)当时,求的极值;(2)设,讨论函数的单调性.【答案】(1)极大值为,极小值为;(2)见解析【解析】试题分析:(1)当时,求得函数的解析式,进而得出,利用和,得出函数的单调性,即可求解函数的极值;(2)由题意知,取得函数,分类和、三种讨论,即可得出函数的单调区间.试题解析:(1)当时,,∴,令,解得或;令,解得,∴在和上单调递增,在上单调递减,∴的极大值为,极小值为.(2)由题意知,函数的定义域为,,由得.①当,即时,恒成立,则函数在上单调递增;②当,即时,令,解得或,令,解得,则函数在和上单调递增,在上单调递减;③当,即时,令,解得或,令,解得,则函数在和上单调递增,在上单调递减.21. 在中,角所对的边分别为,.(1)求的值;(2)若,求外接圆的半径.【答案】(1);(2)【解析】试题分析:(1)由正弦定理化简得,即可解得.(2)由(1)知,根据两角和的正弦公式,求得,再由正弦定理,即可求解外接圆的半径.试题解析:(1)∵,∴,∴,又,. (2)由(1)知,,∵,∴,∴.∴.点睛:本题主要考查解三角形的综合应用问题,其中解答中涉及到解三角形中的正弦定理、三角函数恒等变换等知识点的综合应用,着重考查了学生分析问题和解答问题的能力,其中熟记解三角形中的正弦定理、余弦定理和三角恒等变换的公式是解答的关键,试题比较基础,属于基础题.22. 设函数(为自然对数的底数),.(1)证明:当时,没有零点;(2)若当时,恒成立,求的取值范围.【答案】(1)见解析;(2)【解析】试题分析:(1)由,令,,把没有零点,可以看作函数与的图象无交点,求得直线与曲线无交点,即可得到结论.(2)由题意,分离参数得,设出新函数,得出函数的单调性,求解函数的最小值,即可求解的取值范围.试题解析:(1)解法一:∵,∴.令,解得;令,解得,∴在上单调递减,在上单调递增.∴.当时,,∴的图象恒在轴上方,∴没有零点.解法二:由得,令,,则没有零点,可以看作函数与的图象无交点,设直线切于点,则,解得,∴,代入得,又,∴直线与曲线无交点,即没有零点.(2)当时,,即,∴,即.令,则.当时,恒成立,令,解得;令,解得,∴在上单调递减,在上单调递增,∴.∴的取值范围是.点睛:本题主要考查了导数在函数问题的综合应用,其中解答中涉及到利用导数研究函数的单调性、利用求解函数的极值与最值,以及导数的几何意义等知识点的综合运用,同时着重考查了分离参数思想和构造函数思想方法的应用,本题的解答中根据题意构造新函数,利用新函数的性质是解答的关键,试题综合性强,难度较大,属于难题,平时注重总结和积累.。