当前位置：文档之家 › 场论与数理方程第一章

场论与数理方程第一章

  • 格式：ppt
  • 大小：254.00 KB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

数理方程第1讲-课件

数理方程第1讲-课件
x xy y 3
M u 2u x 2 2u
x 2
y 2
L 2 3 x xy y3
与
M
2 x2
x2
2 y2
都称为微分算子。
我们定义具有下列性质的算子为线性算子。
(1)常数c可以从算子中提取出来 LcucL u
9
(2) 算子作用于两个函数之和所得的结果等于算子分 别作用于两个函数所得结果之和。
例如： 书中例1.1、1.2
y2u2xy2uu1
x2
y2
(二阶线性偏微分方程)
否则称之为非线性偏微分方程。 书中例1.5
7
4. 半线性偏微分方程：若非线性方程中未知多元函 数的所有最高阶偏导数都是线性的，而其系数不含 有未知多元函数及其低阶偏导数，则称为半线性偏 微分方程。如书中例1.6
5. 拟线性偏微分方程：若非线性方程中未知多元函 数的所有最高阶偏导数都是线性的，而其系数含有 未知多元函数或其低阶偏导数，则称为拟线性偏微 分方程。如书中例1.8
6. 非齐次项和非齐次方程：在线性偏微分方程中， 不含未知函数及其偏导数的非零项称为非齐次项， 而含有该非齐次项的方程称之为非齐次方程。如书 中例1.1
8
下面简单讨论一下偏微分方程中经常遇到的线性算子。
算子是一种数学法则，把它作用在一个函数上时，便 产生另外一个函数。例如，在下列表达式中：
Lu u 2u 3u
其中 a2 T , f F.
方程(1.4)称为弦的强迫横振动方程。
16
若外力消失F=0，则方程变为
utta2uxx (a2T)
上式称为弦的自由振动方程。
(1.5)
我们虽然称 (1.4)、(1.5)为弦振动方程，但在力学上弹 性杆的纵振动，管道中气体小扰动的传播以及电报方 程等问题，都可以归结为上述偏微分方程的形式。

数理方程第1讲

数理方程第1讲

CDx
v+Dv
x+Dx
10
L—每一回路单位的串联电感; C—每一单位长度的分路电容. i LDx v x CDx i+Di
v+Dv x+Dx
11
i v (v Dv) LDx t v i L x t
i LD x v x CDx i+Di
(1.4)
v+Dv x+Dx
12
div D (1.11) J—传导电流面密度,—电荷的体密度.
26
D rot H J t B rot E t div B 0 div D
(1.8) （ 1.9) (1.10) (1.11) (1.12)
D E B H J E
(1.13) (1.14)
1
第一章 一些典型方程和定解条件的推导 §1.1 基本方程的建立
2
例1 弦的振动 设有一根均匀柔软的细弦, 平衡时沿直线拉紧, 而且除受不随时间而变的张力作用外, 不受外 力影响. 下面研究弦作微小横向振动的规律. 所谓"横向"是指全部运动出现在一个平面上, 而且弦上的点沿垂直于x轴的方向运动. 所谓"微小"是指的振动的幅度及弦在任意位 置处切线的倾角都很小, 以致它们的高于一次 方的项都可略而不计.
32
例4 热传导方程 在物体中任取一闭曲面S, 它所包围的区域记 作V. 假设在时刻t区域V内点M(x,y,z)处的温度 为u(x,y,z,t), n为曲面元素DS的法向(从V内指向 V外). 由传热学中傅里叶实验定律可知, 物体在无穷 小时间段dt内, 流过一个无穷小面积dS的热量 dQ与时间dt, 曲面面积dS, 以及物体温度u沿曲 面dS的法线方向的方向导数三者成正比

数理方程 - 01 - 数理方程绪论

数理方程 - 01 - 数理方程绪论
201653041总结泛定方程初始条件边界条件dirichletneumannrobin201653042kuhuback第四节定解问题的叠加原理我们考虑一般二阶线性偏微分方程其中abc为常数f为已知函数且则上述方程可以简写为201653043ijijbucu的解则对任意的常数c在求解区域上是一致收敛的并对自变皆可逐项微分两次则u也是该齐次方程的解即lu0其中c是非齐次方程lu根据叠加原理我们可以将复杂的问题分解为一些简单的定解问题进行求解
2015/10/13
11
通解（一般解）
• 一般来讲，一阶偏微分方程的解依赖一个任意函数， 二阶方程依赖两个任意函数。 • 通解或一般解：m 阶偏微分方程的解如果包含有 m 个任意函数。 • 注意：这 m 个函数不能合并，如 f + g 其实就相当于 一个任意函数。
2015/10/13
12
例
• 求 tuxt 2ux 2 xt 的通解
M1

M2 d

O
x
x+x
x
2015/10/13
15
受力分析
3. 惯性力：
▫ 惯性会使物体有保持原有运动状态的倾向，若是以该 物体为参照物，看起来就仿佛有一股方向相反的力作 用在该物体上，故称之为惯性力：F = -ma。 每点的质量为 dm ( x)dx ，每点的加速度为 a utt ， 所有点求和得到积分，即惯性力为
2 ▫ 设 v ux ，则化为 vt v 2 x t
▫ 视 x 为参数，则为关于 v 的一阶常微分方程，
2 2 dt dt 2 2 3 t t ▫ 由求解公式可得 v e 2 xe dt G( x) t G ( x) xt 3

数理方程-第1章第2章-研究生ppt课件

数理方程-第1章第2章-研究生ppt课件
张力为 F T(x,t),F T(x d x,t)与x轴夹角为 1 , 2 . 用 表
示单位长度弦的质量，则长为dx的一小段弦的质量为
d x。u t t 是弦的加速度，及单位长度弦上所受的外力
大小为F(x,t).
16
则根据牛顿第二定律，有
dxuttF T,x dxsin2F T,xsin1F (x,t)dx. F T,xdxcos2F T,xcos10.
uyyuxxA2uxB2uyC2uD2,
双曲型方程的第一标准形和第二标准形。
方程 标准形。
uyy A3uxB3uy C3uD3, 称为抛物型方程的
uxx A4uxB4uy C4uD4,
方程 u x x u y y A 5 u x B 5 u y C 5 u D 5 ,称为椭圆型方程的 标准形。
11
2
2i
变量方程（1）化为标准形 u u A u B u C u D ,
其中A,B,C,D都是 , 的已知函数。
13
第三节 经典方程的导出
一、方程的建立 1、弦振动方程（一维）； 2、热传导方程（一维）；
14
弦的振动方程的导出
（考察一根均匀柔软的细弦，平衡时沿ox轴绷紧） 考察一根长为l的细弦，给定弦的一个初始位移和初始 速度，弦作横振动，确定弦上各点的运动规律。
未知函数u的偏导数。
5
定义：偏微分方程中未知函数的最高阶偏导数的阶 数称为偏微分方程的阶。
定义：如果一个偏微分方程对于未知函数及其各阶 偏导数都是一次的，其系数仅依赖于自变量，就称 为线性偏微分方程。
二阶线性偏微分方程的一般形式：
i,n j1aijx i2 u xj i n1bi x ui cuf(x1, ,xn).

水下物理场总结

水下物理场总结

水下物理场总结第一部分 场论及数理方程基础 场的定义：若对全空间或其中某一区域 V 中每一点 M ，都有一个标量 (或矢量) 与之对应， 则称在 V 上给定了一个标量场 (或矢量场)。

梯度：梯度是由数量函数(,,)u x y z 所定义的向量函数。

散度：设(,,)(,,)i (,,)j (,,)k A x y z P x y z Q x y z R x y z =++为 V上的一个向量场. 称如下数量函数(,,)P Q RD x y z x y z ∂∂∂=++∂∂∂ 为A的散度。

记作div .P Q RA x y z ∂∂∂=++∂∂∂旋度：设(,,)(,,)i (,,)j (,,)k A x y z P x y z Q x y z R x y z =++为V 上的一个向量场. 称如下向量函数 (,,)i +j +k R Q P R Q P F x y z y z z x x y ⎛⎫⎛⎫∂∂∂∂∂∂⎛⎫=--- ⎪ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭ 为 的旋度。

记做r o t i +j RQ P R QA yz zx x⎛⎫⎛∂∂∂∂∂⎛⎫=---⎪ ⎪ ∂∂∂∂∂⎝⎭⎝⎭⎝“源” ：若0div ()0,A M >说明在每一单位时间内有一定数量的流体流出这一点, 则称这一点M 0 为 “源”“汇” ：若 0d i v()0,A M < 说明在每一单位时间内有一定数量的流体流入这一点, 则称这一点M 0 为 “汇”。

第二部分舰船磁场及海洋环境磁场1.地磁场的组成，与地球位置的关系；2.地球偶极子磁场的全球分布规律;3.地磁要素有哪些？地磁坐标系及相应关系4.常见的地磁图有哪几种？5.什么叫太阳日变？简述太阳日变的信号特征及随纬度和季节变化的规律。

6.常见的干扰变化磁场有哪几类？简述地磁脉动干扰的信号特征。

7.什么叫K指数，它是如何规定的？8.什么叫磁暴？发生磁暴时地磁变化场有何特征？9.舰船在地磁场中磁化的特点。

数理方程课件

数理方程课件
详细描述
一阶常微分方程在物理学、工程学、经济学等领域有广泛应用。
一阶常微分方程可以用于描述各种实际问题中变量的变化规律，如物理中的自由落体运动、电路中的电流变化等。在经济学中，一阶常微分方程可以用于描述供求关系的变化、消费和储蓄的动态过程等。在工程学中，一阶常微分方程也广泛应用于控制系统、化学反应动力学等领域。
数理方程可以根据其形式和性质进行分类。
总结词
根据其形式和性质，数理方程可以分为线性与非线性、自治与非自治、常系数与变系数等多种类型。这些分类有助于更好地理解和研究数理方程的性质和应用。
详细描述
数理方程的分类
总结词
数理方程在各个领域都有广泛的应用。
详细描述
数理方程在物理学、工程学、经济学、生物学等许多领域都有重要的应用。例如，在物理学中，描述波动、热传导、引力场等问题的方程都是数理方程。在工程学中，流体动力学、电磁学等领域的问题也都可以通过数理方程来描述和解决。
总结词
一阶常微分方程的定义
一阶常微分方程的解法
求解一阶常微分方程的方法主要有分离变量法、积分因子法、常数变易法和线性化法等。
总结词
分离变量法是将方程中的变量分离出来，使方程变为可求解的形式。积分因子法是通过引入一个因子，使方程变为全微分方程，从而简化求解过程。常数变易法适用于形式为y' = f(x)y的方程，通过代入可求解。线性化法则是将非线性方程转化为线性方程，便于求解。
分离变量法
有限差分法
有限元法
变分法
用离散的差分近似代替连续的微分，适用于求解初值问题和边界问题。
将连续的求解区域离散化为有限个小的子区域，适用于求解复杂的几何形状和边界条件。
通过求某个泛函的极值来求解偏微分方程，适用于求解某些特殊类型的方程。

数理方程 第1章

数理方程 第1章

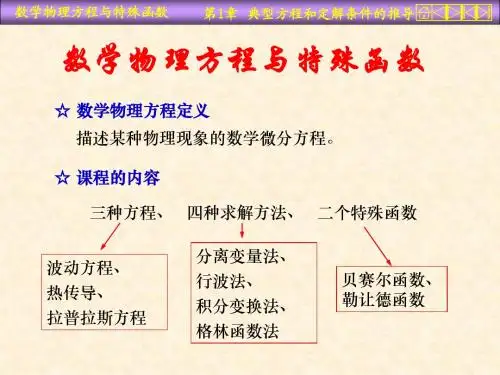
数学物理方程第一章方程的一般概念第一节方程的基本概念•定义：一个含有多元未知函数及其偏导数的方程，称为偏微分方程。

一般形式：其中u 为多元未知函数，F 是以及u 的有限个偏导数的已知函数。

注意：在偏微分方程中可以不含未知函数u ，但必须含有未知函数u 的偏导数。

121112,(,,,,,,,,,)0n n x x x x x F x x x u u u u u L L L 12,,,,n x x x uL–定义：偏微分方程中未知函数的最高阶偏导数的阶数称为偏微分方程的阶。

–定义：如果一个偏微分方程对于未知函数及其各阶偏导数都是一次的，及其系数仅依赖于自变量，就称为线性偏微分方程。

–二阶线性偏微分方程的一般形式：21,11(,,).nnij i n i j i i j i u u a b cu f x x x x x ==∂∂++=∂∂∂∑∑L波动方程热传导方程位势方程2(,)tt xx u a u f x t =+2(,)t xx u a u f x t =+(,)0,(,)(,)0,xx yy f x y Laplace u u f x y f x y Poisson =⎧+=⇒⎨≠⎩方程方程第二节二阶线性偏微分方程的分类一、方程的分类一般形式其中u(x,y)是未知函数，都是x,y 的已知函数，且不同时为零。

称为方程的判别式。

111222122(1)xx xy yy x y a u a u a u bu b u cu f+++++=11122212,,,,,,a a a b b c f111222,,a a a 2121122a a a ∆=-定义:(1)若在处称方程（1）在点处为双曲型方程；(2)若在处称方程（1）在点处为抛物型方程；(3)若在处称方程（1）在点处为椭圆型方程。

00(,)x y 0,∆>00(,)x y 00(,)x y 00(,)x y 00(,)x y 00(,)x y 0,∆=0,∆<例：波动方程双曲型热传导方程抛物型位势方程椭圆型22(,)0tt xx u a u f x t a =+∆=>2(,)0t xx u a u f x t =+∆=(,)1xx yy u u f x y +=∆=-二、方程的标准形式定义：方程分别称为双曲型方程的第一标准形和第二标准形。

1 ch1 数理方程第一章1

1 ch1 数理方程第一章1

∂u ( x2 , t ) Qx2 = − k ∇u • n( x2 ) = − k ∂x
24
• 在 dt 时段内通过微元的两端流入的热量
∂u ( x2 , t ) ∂u ( x1 , t ) dQ1 = −(Qx1 + Qx2 ) dt = k ( ) dt − ∂x ∂x x2 2 ∂ u ( x, t ) = k∫ dxdt 2 ∂x x1
i =1
∞
7
数学物理方程的导出
• 波动方程
– 均匀弦的微小横振动方程 – 推广
• 扩散方程
– 一维热传导方程 – 推广
• 稳定场方程
8
• 弦振动方程
• 弦的特点：匀、细、软、紧的一根弹性细线。 • 振动特性：微小的、横向振动：在一个平面内弦上各点
的运动方向垂直于最初的平衡位置. “微小的”是指弦上各 点的位移与弦的长度相比很小, 弦的纵向伸长可以忽略不 计
数理方程的基本概念
一. 偏微分方程的基本概念
偏微分方程：凡含有多元未知函数及未知函数关于自变量 的偏导数的等式。 自变量 1 2 n
x = (x , x ,
,x )
u ( x) = u ( x1 , x2 ,
, xn )
未知函数
1
偏微分方程: Partial Differential Equation, 简写 为: PDE
在流体柱上任意取一微元在流体柱上任意取一微元处两个截面处两个截面任取一个时段任取一个时段流体在流体在这段时间间隔内从x这段时间间隔内从x处截面流入的质量为处截面流入的质量为处截面流出的质量为处截面流出的质量为所以流体在所以流体在时间间隔内微元中流体净增量为时间间隔内微元中流体净增量为由于在时刻t的流体质量为在时刻的流体质量为由于在时刻t的流体质量为在时刻的流体质量为时间内微元内的流体净增量为时间内微元内的流体净增量为由于流动的连续性和质量守恒因此由于流动的连续性和质量守恒因此上面的方程称为一维的连续性方程

数理方程第一章答案

数理方程第一章答案

第一章． 波动方程§1 方程的导出。

定解条件1．细杆（或弹簧）受某种外界原因而产生纵向振动，以u(x,t)表示静止时在x 点处的点在时刻t 离开原来位置的偏移，假设振动过程发生的张力服从虎克定律，试证明),(t x u 满足方程()⎪⎭⎫ ⎝⎛∂∂∂∂=⎪⎭⎫ ⎝⎛∂∂∂∂x u E x t u x t ρ 其中ρ为杆的密度，E 为杨氏模量。

证：在杆上任取一段，其中两端于静止时的坐标分别为 x 与+x x ∆。

现在计算这段杆在时刻t 的相对伸长。

在时刻t 这段杆两端的坐标分别为：),();,(t x x u x x t x u x ∆++∆++其相对伸长等于 ),()],([)],([t x x u xxt x u x t x x u x x x ∆+=∆∆-+-∆++∆+θ令→∆x ，取极限得在点x 的相对伸长为x u ),(t x 。

由虎克定律，张力),(t x T 等于),()(),(t x u x E t x T x =其中)(x E 是在点x 的杨氏模量。

设杆的横截面面积为),(x S 则作用在杆段),(x x x ∆+两端的力分别为x u x S x E )()(x u x x S x x E t x )()();,(∆+∆+).,(t x x ∆+于是得运动方程 tt u x x s x ⋅∆⋅)()(ρxESu t x =),(x x x x x ESu x x |)(|)(-∆+∆+利用微分中值定理，消去x ∆，再令0→∆x 得ux s x )()(ρx∂∂=xESu()若=)(x s 常量，则得22)(tu x ∂∂ρ=))((xu x E x∂∂∂∂即得所证。

2．在杆纵向振动时，假设(1)端点固定，(2)端点自由，(3)端点固定在弹性支承上，试分别导出这三种情况下所对应的边界条件。

解：(1)杆的两端被固定在l x x ==,0两点则相应的边界条件为 .0),(,0),0(==t l u t u(2)若l x =为自由端，则杆在l x =的张力xu x E t l T ∂∂=)(),(|l x =等于零，因此相应的边界条件为xu ∂∂|l x ==0同理，若0=x 为自由端，则相应的边界条件为xu ∂∂∣00==x(3)若l x =端固定在弹性支承上，而弹性支承固定于某点，且该点离开原来位置的偏移由函数)(t v 给出，则在l x =端支承的伸长为)(),(t v t l u -。

数理方程1

数理方程1
u = u ( x, y ) : u xx + u yy = 0(调和方程) Δ = 0 − 1 ⋅ 1 = −1 < 0, 椭圆型
2.1 分类与化简 目标: 通过自变量变换,使方程的形式简化,甚至可以求 出其通解 ⎧ξ = ξ ( x, y ) 自变量变换 ⎨
α = (α1 ,L, α n ), α = α1 + L + α n .
半线性(Semi-Linear)：主部(含最高阶导数的部分)线性
Aα ( x) Dα u + A ( x, u , Du, K , D ∑ α
=N 0
N −1
u ) = g ( x),
拟线性(Quasi-Linear)：最高阶导数是线性的
∑ Aα ( x, u, Du,K, D α
=N
N −1
u)Dα u
x x0 y 0
∫
y
w( s, t )dsdt + f ( x) + g ( y )
( f , g为任意连续可微函数)
(4)u = u ( x, y ) : u x = u y 作变量代换s = x + y, t = x − y ⇒ u x = u s s x + ut t x = u s + ut u y = u s s y + ut t y = u s − ut ⇒ us = 0 ⇒ u = f (t ) ( f为任意函数) ⇒ u ( x, y ) = f ( x − y ) 一般地，au x + bu y = 0 (a, b为常数) ⇒ u = f (bx − ay )
b
b
解：设( x1 ,L, x n ) ∈ Ω(求解区域)，若函数 u = u ( x1 ,L, x n )在Ω内足够光滑并且在Ω内 恒满足偏微分方程(*), 则称u为(*)的经典解

数理方程第一章

数理方程第一章

6、求解方法
分离变量法、行波法、积分变换法、格林函数法
数学物理方程与特殊函数
第1章 典型方程和定解条件的推导
简化假设： (1)弦是柔软的，弦上的任意一点的张力沿弦的切线方向。 (2)振幅极小， 张力与水平方向的夹角很小。 牛顿运动定律： 横向： T cos α = T 'cos α ' 纵向： T sin α + T 'sin α '− ρ gds ≈ ma − 其中：cos α ≈ 1 cos α ' ≈ 1
2
4、叠加原理
线性方程的解具有叠加特性
Lui = f i
∑f
i
=f
∑u ∑u
i
i
=u
Lu = f
Lu = 0
Lui = 0
=u
几种不同的原因的综合所产生的效果等于这些不同原 因单独产生的效果的累加。(物理上)
数学物理方程与特殊函数
第1章 典型方程和定解条件的推导
5、微分方程的解
古典解：如果将某个函数 u 代入偏微分方程中，能使方程成 为恒等式，则这个函数就是该偏微分方程的解。 通解： 解中含有相互独立的和偏微分方程阶数相同的任意 常数的解。 特解： 通过定解条件确定了解中的任意常数后得到的解。 形式解：未经过验证的解为形式解。
v n
M
温度发生变化需要的热量为： Q2 = ∫∫∫ cρ [u ( x, y, z , t 2 ) − u ( x, y, z , t1 )]dV V t2 t 2 ∂u ∂u = ∫∫∫ cρ ∫ dtdV = ∫t ∫∫∫ cρ dVdt t1 ∂t 1 ∂t V V
Q1 = Q2
2
热场
∫ ∫∫∫ k∇ udV dt = ∫

数理方程第一章、第二章习题全解

数理方程第一章、第二章习题全解

u( 0 , t) = u( l, t) = 0 现考虑初始条件,当冲量 k 作用于 x = c处时, 就相当于在这点 给出了一个初速度 , 我们考虑以 c点为中心 , 长为 2δ的一小段弦 ( c δ, c + δ) , 设弦是均匀的 , 其线密度为 ρ, 则这 一小段 弦的质量 为 2δρ, 受冲击时速度为 ut ( x, 0) , 由动量定理得
h c
x
l
h -
c(
l
-
x)
(0 ≤ x ≤ c) ( c < x ≤ l)
ut ( x, 0) = ψ( x ) = 0
则 u( x, t) 是下列定解问题的解 :
utt - a2 uxx = 0
( 0 < x < l, t > 0)
u( x, 0) = φ( x ) , ut ( x, 0 ) = ψ( x )
2 .4 习题全解
1. 设弦的两端固定于 x = 0 及 x = l, 弦的初始位称如图 2 2 所 示,初速度为零, 又设有外力作用, 求弦作横向振动时的位移函数 u( x, t) 。
解 如图 2 2 所示, 弦作横向振动时初始条件为
62
数学物理方程与特殊函数导教·导学·导考
图2 2
u( x, 0) = φ( x ) =
5. 若 F( z) , G( z) 是任意两个二次连续可微函数 , 验证
u = F( x + at ) + G( x - at )
满足方程
2u t2
=
a2
2x2u。
解 作自变量代换ξ= x + at,η= x - at, 由复合函数求导法则
有
所以 于是
u t

数理方程 第一章

数理方程 第一章

uபைடு நூலகம்
1 (u u ) 6( )
20
y 0
Tricomi方程变为
u yy 0
这就是抛物型的标准形式。
21
第三节 定解问题的适定性
定解 问题 PDE 初值条件
定解条件
边值条件
初、边值条件
初值问题、边值问题、混合问题
22
经典的定解问题举例
波动方程的初值问题（一维）
2 2u u 2 f ( x, t ), t 0, x R 2 a 2 x t u ( x, t ) ( x) t 0 u ( x, t ) ( x) t 0 t
非奇异
x y 0 x y
5
u ( x, y )
复合求导
( x, y ) ( x, y )
u ( , )
u u u x x x u u u y y y
2u 2u 2 2u 2u 2 u 2 u 2 ( ) 2 ( ) 2 2 2 2 x x x x x x x 2 2u 2u 2u 2u u 2 u 2 2 ( ) 2 xy x y x y x y x y xy xy 2u 2u 2 2u 2u 2 u 2 u 2 ( ) 2 ( ) y 2 2 y y y 2 y y 2 y 2
数学物理方程 第一章
第一节 偏微分方程的基本概念
x ( x1 , x2 ,, xn )
u( x) u( x1, x2 ,, xn )
2
自变量
未知函数
u u u F ( x, u, ,, , 2 ,) 0 x1 xn x1

数学物理方程第一章矢量分析与场论基础(20200511214611)

数学物理方程第一章矢量分析与场论基础(20200511214611)

第一章矢量分析与场论基础 内容提要 1）正交曲线坐标系：设有三组互相正交的曲面族由下列方程定义:q ! =qdx, y,z ）q ?二q 2（x,y,z ） q ? =q 3（x,y,z ）在正交曲线坐标中的线元、面元、体元分别为dl i =hi dq idh ph j dq j■卡FdS i =dl j dl k = ?h j h k dq j dq kdv 二 dh dl j dl^ h i h j h k dq i dq j dq k式中 i 、 j 、 k 代表循环量 1、2、3， q? = ?jc?k ， （?i （?j （?k =1 ,的-sin 日 0 cos 日］=cos 。

0 si n 日■0 1 0 一球坐标与柱坐标球坐标与直角坐标2）矢量及其运算：直角坐标中算符I 的定义:-cos®sin ®= -s in ® cos®1 -0 0 oe y柱坐标与直角坐标sin 二 cos：cos 日sin 二sin ： cos ^sin :cos 日 1 @x Ih i称拉梅系数。

三种坐标系中坐标单位矢量间的关系:一个标量函数u 的梯度为:梯度给出了一点上函数 u 随距离变化的最大速率，它指向u 增大的方向。

一个矢量F 穿过一个曲面S 的通量’-：为屮=[F dSS对一个闭合曲面而言， ds 向外为正。

直角坐标系中F 的散度表示在这一点上每单位体积向外发散的F 的通量。

散度定理：' Fdv F dsV-S其中v 是由S 所包围的体积。

斯托克斯定理：f F) ds — F dl其中s 是由I 所包围的面积。

直角坐标系中F 的旋度拉普拉辛是梯度的散度e x.:x-y.:F y ■:y:z@.£cz Lr0?◎一 e xVx F =— u _u c'心二ex»e y散度的体积分=矢量的面积分旋度的面积分=矢量的线积分一个矢量的拉普拉辛定义为:'、2F 八乍x ?x• '、2F y ?y\ 2F z e Z其它坐标也可写成:于F x =可(可F)—可XV X F柱坐标系中r 二zZ?zdr 二 d T ?!：亠 ed g ： dze zdv 二-:d :d :dz球坐标系中dv 二 r 2 sin ^drd 巾‘f▲r~\Ar~\"弋耳1寺？乔岂？在直角坐标系中: 2■■ ?u -u2 2；：u j u~~2:x:y—F -匕壬丄壬圭P cP.:zVx\2u J-：u P cP ?pFp:?:F ::?z .z F z-2-?21 ：：2u ：：2u尹戸TZ7dr = dr?rd r sin 刃?r 2sin日V F =c rF rr sin 日rEc0r F日r sin0F(p2赴(•口£U 1 d u(sin E —) * —2 2 2&日r2sin2日砂2矢量场F可表示为一个无旋场分量和一个无散场分量之和F 二F e F l其中F=F l C ・F e =0）可x F =可汇F e（可汇F| = 0）因此一个矢量场要从散度和旋度两个方面去研究4）二函数宀勺I 0（r式r'）疋乂：6（r —r）=丿' -一'迂（r=r）⑹甘）d-」0（F在v#）v J（r在v内）性质a）偶函数:、（x）—（-x）b）取样性：__ f（X）、（x-a）dx 二f （a）有机会用到的表达式:1-1.证明：A B =($9 e y2 -e z®($2 色3 e z4)=18+6-24----------------r2 sin v ：r3）亥姆霍兹定理:=0说明A 与B 相互垂直1-2.空白 1-3.证明：A B = A x B x A y B y A z B z = 0说明A 与B 相互垂直1-4.解：当坐标变量沿坐标轴由 u i 增至u i dm 时，相应的线元矢量dl i 为:dl i =(5 duj - (U i )3其中二？1X 1 X 2X 2 X 3X 3 二' ?j ?j11-5.解：(1)据'算子的微分性质，并按乘积的微分法则，有=?其中弧长则dl i 二 hdu i'、、(A B)二'、(A c B) '、(A B e)其中A c、B e暂时视为常矢，再根据二重矢量积公式a (b c) = (a c)b -(a b)c将上式右端项的常矢轮换到' 的前面，使变矢都留在 ' 的后面A c二a 、(Ac B)二A c C B) (A c \ )BB e = a I (A ・B c) = B c (* ■：A) ■ (B e )A则、 A) (B c ' )A l (A B)二A c C B) (A c h)B B c ('除去下标c即可、(A B)=A C B) (A )B B C A) (B 人)A⑵利用⑴式的结果即可。

数理方程第一章-3讲解

数理方程第一章-3讲解

a2
(
2u x2
2u y2
2u z2
)
u t
a2 k c
—— 三维热传导方程
本课程内容，只涉及线性边界条件，且仅包括以下三类。
深圳大学电子科学与技术学院
第一类边界条件：物理条件直接规定了 u 在边界上的值，如
u S
f1
第二类边界条件：物理条件并不直接规定了 u 在边界上的值，而是规定了u 的法向微商在边界上的值，如
深圳大学电子科学与技术学院
知识补充：
弹性模量是指当有力施加于物体或物质时，其弹性变 形（非永久变形）趋势的数学描述。物体的弹性模量 定义为弹性变形区的应力－应变曲线的斜率。杨氏模 量指的是受拉伸和压缩时的弹性模量。
杨氏模量(Young‘s modulus)是描述固体材料抵抗形变 能力的物理量。一条长度为L、截面积为S的金属丝在 力F作用下伸长L。F/S叫应力，其物理意义是金属丝 单位截面积所受到的力； L/L叫应变，其物理意义是 金属丝单位长度所对应的伸长量。
dx
x
不考虑垂直杆方向的形变，根据Hooke定律，应力与应变成正
比，即 P E u x
代入
P x
2u t 2
2u t2
a2
2u x2
0 xl , t0
其中
a2 E
深圳大学电子科学与技术学院
例6：一根均匀杆，原长为l，一端固定，另一端沿杆的轴线方向被拉长e而静 止。突然松手，任其纵向振动。写出定解问题。
（3）对于稳恒场，上述边界条件的两端均不含时间 t ; （4）边界条件的推导，步骤与泛定方程的推导大致相同，但微元只能在边界上选取。
x
x
S 2u d x
t2
Sdx dm（微元质量）
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

u
T2
B
α1
T1
α2
C
A
x
x + dx
图9.1
x
作用于小段 ABC 的横向合力应该为零：
T2 cos 2 T1 cos 1 0
仅考虑微小的横振动， 夹角
（1）
1 , 2 为很小的量，忽略 12 , 22
及其以上的高阶小量，则根据级数展开式有
12 cos 1 1 1, 2!
（2）
sin 2 2 tan 2
ds (dx)2 (du)2 1 (ux )2 dx dx
注意到:
u ux tan sin 故由上图得 x
ux x tan 1 sin 1 ,
这样，(1)和(2)简化为
ux
x dx
tan 2 sin 2
差分方法 有限元 多尺度

古典解

程和定解条件的推导
§1.1 基本方程的建立 一、弦振动方程
例1：设一长为l的均匀柔软的细弦，导出弦的微小的横振动方 程
u
T2
u ( x, t )
B
α1
T 1
α2
C
A
x
x + dx
图9.1
x
横振动：1.在同一平面内振动 2.振向与弦向垂直
(5)
dx
x dx
可以取得很小，根据微分知识有下式成立
ux
因此
ux
x
u x dx u xx dx x
utt Tuxx g 0
(6)
utt a 2uxx g
其中 a 2 T / 讨论：
（7）
上式即为弦作微小横振动的运动方程，简称为弦振动方程．
（1）若设弦的重量远小于弦的张力，则上式(7)右端的重力 加速度项可以忽略．由此得到下列齐次偏微分方程：
utt a uxx
2
（8）
称式（8）为一维弦振动方程（一维波动方程）
(2) 如果在弦的单位长度上还有横向外力F ( x, t ) 作用，则式(2)应该改写为
T1 sin 1 T2 sin 2 gds F ( x, t )ds dsutt
可导出
utt a uxx f ( x, t )
数学物理方程
微分方程

常微分方程
u ( x)
u f ( x) x

偏微分方程
u ( x, t ) （其中x表示位置，t表示时间） v( x, n) （其中x表示大小，n表示方向）
2u 2u 2 f ( x, t ) 2 x t
数学物理方程

数学物理方程：用数学方法研究物理现象的偏微分 方程。 经典方程
T2 u x x dx T1 u x x gdx utt dx T2 T1 0
（3） (9.1.3) （4） (9.1.4)
T2 T1
，弦中张力不随
可记为 x 而变，
T T2 T1 故有
T (ux
变化量
x dx
ux x ) gdx utt dx


波动方程 热传导方程 调和方程
数学物理方程的发展

对流扩散方程 奇异摄动方程
2u u u a 2 b f ( x, t ) x x t 2u u 1 2 2 f ( x, t ) x x


弹性力学
数学物理方程的解法

分析解法

分离变量法 积分变换法 行波法
2
(9)
式中 f ( x, t )
F ( x, t )

称为力密度
式（9）称为弦的受迫振动方程.
cos 2 1
T1 T2
u
T2
B
α1
T1
α2
C
A
x
x + dx
图9.1
x
根据牛顿第二定律 F ma u 方向运动的方程可以描述为
T2 sin 2 T1 sin 1 gds (ds)utt
13 sin 1 1 1 tan 1 , 3!