关于等量同种或者一种电荷场强分布

等量同种、异种电荷电场强度和电势的定量比较作者：杨杰来源：《理科考试研究·高中》2015年第02期平常教学中，关于等量同种、异种电荷连线上电场强度和电势的比较，往往更多地根据电场线的方向和分布定性地说明.由于电场线本身并不是客观存在的，而是人为引入的，再加上电场概念本身又比较抽象，不少同学对结论心存疑惑，更希望能够通过定量计算得出更具说服力的结论.笔者尝试着进一步分析发现，的确也可以通过定量计算进行说明，教学中也收到了理想的效果.一、等量同种电荷的电场强度和电势1.等量同种电荷的连线上①电场强度从电场线分布定性分析，a→o→b，由于电场线先变疏，后变密，所以电场强度先减小后增大.定量计算：设︱ab︱=L，︱aA︱=x，EA=kQx2，kQ（L-x）2，a→o过程中（x≤L2），x 变大， kQx2减小，kQ（L-x）2增大，∴EA减小.当x=L2时，Emin=Eo=0.由对称性可知，o→b过程中，电场强度不断增大.所以，a→o→b电场强度先减小后增大.②电势从电场方向定性分析，a→o，电场方向向右，o→b，电场方向向左.沿电场线方向电势降低.所以a→o→b，电势先减小后增大.定量计算：取无穷远处Ep=0，WA→∞=EPA-0，距电荷+Q距离为r处的A点的点电荷+q 的电势能，等于把它从这点移动到零势能位置时静电力做的功.EPA=WA→∞=∫∞rkQqr2dr=kQqr，则A点的电势φA=kQr.所以，到点电荷Q距离为r处的电势为φ=kQr（Q含正负，即正电荷在其周围产生的电势为正，负电荷在其周围产生的电势为负）.在A点，a处的+Q在A点产生的电势为φ=kQx，b处的+Q在C点产生的电势为φ=kQL-x，所以等量同种电荷连线上的A点的电势φA=kQx+kQL-x=kQLx（L-x）=kQLL24-（L2-x）2，a→o过程中（x≤L2），x变大，φA减小，当x=L2时，φmin=4kQL.由对称性可知，o→b过程中，电势不断增大.所以，a→o→b，电势先减小后增大.2.等量同种电荷的中垂线上①电场强度从电场线分布定性分析，o→∞，电场线先变密，后变疏，所以，电场强度先增大后减小.定量计算：EC=2E1cosθ=8kQL2sin2θcosθ=42kQL22cos2θsin2θsin2θ.当2cos2θ=sin2θ时，即tanθ=2，场强有最大值Emax=1630kQL2.所以o→∞，电场强度先增大后减小.②电势从电场方向定性分析，电场方向沿o→∞方向.o→∞，电势降低.定量计算：a、b处的+Q在C点产生的电势均为kQL2sinθ=2kQsinθL所以φC=4kQsinθL，θ减小，φC减小，当θ=90°时，电势最高，φ0=φmax4kQL.所以o→∞，电势一直减小.二、等量异种电荷的电场强度和电势1.等量异种电荷的连线上①电场强度从电场线分布定性分析，a→o→b，由于电场线先变疏，后变密，所以电场强度先减小后增大.定量计算：同样设︱ab︱=L，︱aA︱=x，则EA-EO=kQx2 +kQ（L-x）2-8k QL2≥kQ[2x （L-x）2-8L2]=2kQ（L-2x）2x（L-x）L2≥0，所以EA≥EO，o点的电场强度最小，由对称性可知，a→o→b电场强度先减小后增大.②电势从电场方向定性分析，电场方向沿a→b方向，所以，a→b电势一直减小.定量计算：+Q在A点产生的电势为φ=kQx，-Q在C点产生的电势为φ=-kQL-x，所以φA=-kQx-kQL-x=kQ（L-2x）x（L-x），x增大，x（L-x）增大，（L-2x）减小，φA减小.所以，a→b电势一直减小.2.等量异种电荷的中垂线上①电场强度从电场线分布定性分析，o→∞，由于电场线越来越疏，所以，电场强度一直减小.定量计算：中垂线上任取一点C，Ec=8kQL2sin3θ，θ越小，EC越小.∴o→∞，E一直减小.②电势从电场方向定性分析，电场方向垂直于中垂线，沿o→∞方向移动电荷，电场力不做功，所以，o→∞，电势不变，且与无穷远处电势相等（电势为零）.定量计算：+Q在C点产生的电势为φ=2kQsinθL，-Q在C点产生的电势为φ=-2kQsinθL.所以φC=0，o→∞，电势始终为0，中垂线为等势线.由此可见，无论通过定量计算还是定性分析，都会得出同样的结论.而定量分析能让学生经历概念规律的探究过程，使得原本抽象难懂的知识真实地呈现在学生眼前，加深了学生对同种、等量异种电荷的电场强度和电势的理解，有助于学生更好地解决与此相关的各类问题.下面笔者以一道典型的高考题为例，说明相关知识在解决实际问题中的重要作用.例1（2010年江苏单科第5题）空间有一沿x轴对称分布的电场，其电场强度E随x变化的图象如图所示.下列说法中正确的是（）.A.O点的电势最低B.x2点的电势最高C.x1和-x1两点的电势相等D.x1和x3两点的电势相等解析由题图知，该图象所反映的电场的特点：①在O处，场强为零，但电势最高；②在x1和-x1两点处，场强大小相等，方向相反，电势相等；③在x1和x3两点处，场强相同，但电势不同.由此可知，这个电场不是一个点电荷的电场，可能是两个点电荷形成的电场；从x=0到正负无穷远，场强有一个最大值，电势逐渐减小；当x趋近于正负无穷远时，场强和电势均为零.说明这是两个等量同种正电荷中垂线上的电场分布（如图所示）.如果画出图象如右图所示，这就是09年江苏高考的第8题.同一个物理情境可以从不同的角度考查，但只要对等量同种、异种点电荷的电场、电势有准确的理解，问题自然就迎刃而解.答案C例2（2013年天津理综第6题）两个带等量正电的点电荷，固定在图中P、Q两点，MN 为PQ连线的中垂线，交PQ于O点，A点为MN上的一点.一带负电的试探电荷q，从A点由静止释放，只在静电力作用下运动.取无限远处的电势为零，则（）.A.q由A向O的运动是匀加速直线运动B.q由A向O运动的过程电势能逐渐减小C.q运动到O点时的动能最大D.q运动到O点时电势能为零解析等量正电荷连线的中垂线上，电场方向由O指向A，o→∞，电场强度先变大后变小，O点电场强度为零，A点电场强度大于零.又由于A点是中垂线上的任意一点，不一定是电场最强的特殊点，所以A到O的过程加速度是变化的，但不能确定是如何变化的，可能是一直减小，也可能先增大后减小.所以，A错误.带负电的试探电荷q，从A点由静止释放，所受静电力由A指向O，只在静电力作用下运动，A向O运动，电场力做正功，动能增加，电势能减小.取无限远处的电势为零，到O点时电势能为负，动能最大，所以，选项D错误，BC 正确.电场力减小，加速度逐渐减小的加速运动，q由A向O运动的过程电势能逐渐减小，q运动到O点时的动能最大，电势能不为零，AD错误.答案BC。

精心整理
精心整理 等量电荷的电场分布
等量正电荷等量负电荷等量异种电荷
等量异种与等量同种点电荷连线和中垂线上场强的变化规律：
（1）等量异种点电荷连线上中点场强最小，中垂线上各点中点的场强最大；等量同种点电荷连线上中点场强最小，等于零。

因为无穷远处场强为零，则沿等量同种点电荷中垂线从中点到无穷远处，电场强度先增大后减小，中间某位置必有最大值。

（2）等量异种点电荷连线和中垂线上关于中点对称处的场强相同；等量同种点电荷连线和中垂线
（1（2
）等量异种点电荷的连线上，从正电荷到负电荷电势越来越低，中垂线是一等势线，若沿中垂线移动电荷至无穷远，电场力不做功，因此若取无穷远处电势为零，则中垂线上各点的电势也为零．因此从中垂线上某点不沿中垂线移动电荷到无穷远，电场力做功仍为零．。

等量电荷两条线上的场强分布特点等量同种（异种）点电荷在空间的场强分布比较复杂，但在两条线（点电荷连线及其中垂线）上仍有其规律性，为研究方便，设它们带电量为Q，两电荷连线AB长度为L,中点为O.一、等量异种电荷1、两电荷连线上如图1所示，在两电荷连线上任取一点G，设AG长度为x，则G点场强EG为两点电荷分别在该点的场强EA、EB的矢量和，方向从A指向B（由正电荷指向负电荷一侧），由点电荷场强公式知：EG= EA+ EB=∵x+(L-x)等于定值L，∴当x=(L-x)，即x= 时，x与(L-x)乘积最大，EG有最小值，即在两电荷连线中点O处场强最小，从O点向两侧逐渐增大，数值关于O点对称。

2、中垂线上如图2所示，在中垂线上，任取一点H，设OH=x，根据对称性知：EH沿水平方向向右，即在中垂线上各点场强水平向右（垂直于中垂线指向负电荷一侧），沿中垂线移动电荷，电场力不做功，由电势差定义知：中垂线为一等势线，与无限远处等势，即各点电势为零。

H点的场强EH=，∴在O点，即x=0处，EH最大，x越大，即距O点越远EH越小，两侧电场强度数值关于O 点对称。

二、等量同种电荷1、电荷连线上如图3所示，在两电荷连线上任取一点N，设AN长度为x，则N点场强EN为两点电荷在该点的场强EA、EB的矢量和，方向沿AB连线，O点左侧从A指向B，右侧从B指向A（沿两电荷连线指向较远一侧电荷，若两电荷为等量负电荷则反之），N点电场强度大小知：EN = ，∴当x= 时，EN =0，，即在两电荷连线中点O处场强最小，从O点向两侧逐渐增大，数值关于O点对称，方向相反。

2、中垂线上如图4所示，根据对称性知：在O点两侧，电场强度方向均沿中垂线方向从O点指向无限远（若两电荷为等量负电荷则反之），由极限分析法易得：在O点处，E =0；在距O点无限远处，E =0。

说明中间某位置有极大值，可见：合电场强度的大小随着距O点的距离增大，先从零增大到最大，然后逐渐减小。

关于等量点电荷周围场强和电势的分布特点作者：田军来源：《试题与研究·教学论坛》2017年第24期等量点电荷在空间的场强分布比较复杂，但在两条线（点电荷连线及其中垂线）上仍有其规律性，为研究方便，设它们带电量为Q，两电荷连线AB长度为L，中点为O。

一、等量的同种电荷形成的电场的特点1.场强特点①两点电荷连线上：任取一点P，设AP长度为x，则P点场强EP为两点电荷在该点的场强EA、EB的矢量和，方向沿AB连线，O点左侧从A指向B，右侧从B指向A（沿两电荷连线指向较远一侧电荷，若两电荷为等量负电荷则反之）。

P点电场强度大小知：EP=，∴当x=时，EP=0，即在两电荷连线中点O处场强最小，从O点向两侧逐渐增大，数值关于O点对称，方向相反。

②两点电荷连线的中垂线上：在O点两侧，电场强度方向均沿中垂线方向从O点指向无限远（若两电荷为等量负电荷则反之），由极限分析法易得：在O点处，E=0；在距O点无限远处，E=0。

说明中间某位置有极大值，可见：合电场强度的大小随着距O点的距离增大，先从零增大到最大，然后逐渐减小。

在中垂线上，任取一点P，设OP=x，由点电荷场强公式，P 点场强EP=2EAcosθ==运用数学方法，令y=，求导可得：y=令y′=0，则x2+2=3x2x2+2，即x2+2=3x2，∴当x=±L时，EP有最大值，∴从中点沿中垂线向两侧，电场强度的数值先增大后减小，两侧方向相反，关于O点对称的点数值相等。

2.电势特点①中点O点处的电势：φO=φA+φB=4>0②两点电荷连线上任意一点P处的电势：总结：在两个等量正电荷的连线上，由A点向B点方向，电势先减后增，在rA=R/2（即中点O处）电势最小，但电势总为正。

③两点电荷连线的中垂线上任意一点Q处的电势：总结：在两个等量正电荷的连线的中垂线上，由O点向N（M）点方向，电势一直减小且大于零，即O点最大，N（M）点为零。

二、等量的异种电荷形成的电场的特点1.场强特点①两电荷连线上任取一点G，设AG长度为x，则G点场强EG为两点电荷分别在该点的场强EA、EB的矢量和，方向从A指向B（由正电荷指向负电荷一侧），由点电荷场强公式知：∵x+（L-x）等于定值L，∴当x=（L-x），即x=时，x与（L-x）乘积最大，EG有最小值，即在两电荷连线中点O处场强最小，从O点向两侧逐渐增大，数值关于O点对称。

几种典型电场线分布示意图及场强电势特点表一、场强分布图孤立点电荷周围的电场等量异种点电荷的电场等量同种点电荷的电场+匀强电场－－－－点电荷与带电平二、列表比较下面均以无穷远处为零电势点，场强为零。

电场线直线，起于正电荷，终止于无穷远。

孤立离场源电荷越远，场强越小；与场源电荷等距的各点组成的球面上场强大小相等，方向不场强的同。

正点离场源电荷越远，电势越低；与场源电荷等距的各点组成的球面是等势面，每点的电势为电势电荷正。

等势面以场源电荷为球心的一簇簇不等间距的球面，离场源电荷越近，等势面越密。

电场线直线，起于无穷远，终止于负电荷。

孤立离场源电荷越远，场强越小；与场源电荷等距的各点组成的球面上场强大小相等，方向不场强的同。

负点离场源电荷越远，电势越高；与场源电荷等距的各点组成的球面是等势面，每点的电势为电势电荷负。

等势面以场源电荷为球心的一簇簇不等间距的球面，离场源电荷越近，等势面越密。

电场线大部分是曲线，起于无穷远，终止于负电荷；有两条电场线是直线。

等量电势每点电势为负值。

同种连以中点最小为零；关于中点对称的任意两点场强大小相等，方向相反，都是背离中负点场强线点；由连线的一端到另一端，先减小再增大。

电荷上电势由连线的一端到另一端先升高再降低，中点电势最高不为零。

中以中点最小为零；关于中点对称的任意两点场强大小相等，方向相反，都沿着中垂场强垂线指向中点；由中点至无穷远处，先增大再减小至零，必有一个位置场强最大。

线中点电势最低，由中点至无穷远处逐渐升高至零。

电势上电场线大部分是曲线，起于正电荷，终止于无穷远；有两条电场线是直线。

电势每点电势为正值。

连以中点最小为零；关于中点对称的任意两点场强大小相等，方向相反，都是指向中等量场强线点；由连线的一端到另一端，先减小再增大。

同种上电势由连线的一端到另一端先降低再升高，中点电势最低不为零。

正点中以中点最小为零；关于中点对称的任意两点场强大小相等，方向相反，都沿着中垂电荷场强垂线指向无穷远处；由中点至无穷远处，先增大再减小至零，必有一个位置场强最大。

两等量同种（异种）电荷场强分布特点等量同种（异种）点电荷在空间的场强分布比较复杂，但在两条线（点电荷连线及其中垂线）上仍有其规律性，为研究方便，设它们带电量为Q ，两电荷连线AB 长度为L,中点为O.一、 等量异种电荷1、 两电荷连线上如图1所示，在两电荷连线上任取一点G ，设AG 长度为x ，则G 点场强E G 为两点电荷分别在该点的场强E A 、E B荷指向负电荷一侧），由点电荷场强公式知：E G = E A + E B =()[]()[]22222)(xL x xx L L kQ x L kQ x kQ ---=-+∵x+(L-x)等于定值L ，∴当x=(L-x)，即x=2L时，x 与 (L-x)乘积最大， E G 有最小值，即在两电荷连线中点O 处场强最小，从O 点向两侧逐渐增大，数值关于O 点对称。

2、 中垂线上如图2所示，在中垂线上，任取一点H ，设OH=x ，根据对称性知：E H 沿水平方向向右，即在中垂线上各点场强水平向右（垂直于中垂线指向负电荷一侧），沿中垂线移动电荷，电场力不做功，由电势差定义知：中垂线为一等势线，与无限远处等势，即各点电势为零。

H 点的场强E H =232222222222222cos 22⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛=+⎪⎭⎫ ⎝⎛⋅+⎪⎭⎫ ⎝⎛=⋅+⎪⎭⎫ ⎝⎛x L kQL x L L x L kQ x L kQ θ，∴在O 点，即x=0处，E H 最大，x 越大，即距O 点越远E H 越小，两侧电场强度数值关于O 点对称。

图1G O B图2H二、 等量同种电荷1、 电荷连线上如图3所示，在两电荷连线上任取一点N ，设AN 长度为x ，则N 点场强E N 为两点电荷在该点的场强E A 、E B 的矢量和，方向沿AB 连线，O 点左侧从A 指向B ，右侧从B 指向A （沿两电荷连线指向较远一侧电荷，若两电荷为等量负电荷则反之），N 点电场强度大小知：E N =22)(x L kQx kQ --， ∴当x=2L时，E N =0，，即在两电荷连线中点O 处场强最小， 从O 点向两侧逐渐增大，数值关于O 点对称，方向相反。

两等量同种（异种）电荷场强分布特点等量同种（异种）点电荷在空间的场强分布比较复杂，但在两条线（点电荷连线及其中垂线）上仍有其规律性，为研究方便，设它们带电量为Q ，两电荷连线AB 长度为L,中点为O.一、 等量异种电荷1、 两电荷连线上如图1所示，在两电荷连线上任取一点G ，设AG 长度为x ，则G 点场强E G 为两点电荷分别在该点的场强E A 、E B荷指向负电荷一侧），由点电荷场强公式知：E G = E A + E B =()[]()[]22222)(xL x xx L L kQ x L kQ x kQ ---=-+∵x+(L-x)等于定值L ，∴当x=(L-x)，即x=2L时，x 与 (L-x)乘积最大， E G 有最小值，即在两电荷连线中点O 处场强最小，从O 点向两侧逐渐增大，数值关于O 点对称。

2、 中垂线上如图2所示，在中垂线上，任取一点H ，设OH=x ，根据对称性知：E H 沿水平方向向右，即在中垂线上各点场强水平向右（垂直于中垂线指向负电荷一侧），沿中垂线移动电荷，电场力不做功，由电势差定义知：中垂线为一等势线，与无限远处等势，即各点电势为零。

H 点的场强E H =232222222222222cos 22⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛=+⎪⎭⎫ ⎝⎛⋅+⎪⎭⎫ ⎝⎛=⋅+⎪⎭⎫ ⎝⎛x L kQL x L L x L kQ x L kQ θ，∴在O 点，即x=0处，E H 最大，x 越大，即距O 点越远E H 越小，两侧电场强度数值关于O 点对称。

图1G O B图2H二、 等量同种电荷1、 电荷连线上如图3所示，在两电荷连线上任取一点N ，设AN 长度为x ，则N 点场强E N 为两点电荷在该点的场强E A 、E B 的矢量和，方向沿AB 连线，O 点左侧从A 指向B ，右侧从B 指向A （沿两电荷连线指向较远一侧电荷，若两电荷为等量负电荷则反之），N 点电场强度大小知：E N =22)(x L kQx kQ --， ∴当x=2L时，E N =0，，即在两电荷连线中点O 处场强最小， 从O 点向两侧逐渐增大，数值关于O 点对称，方向相反。

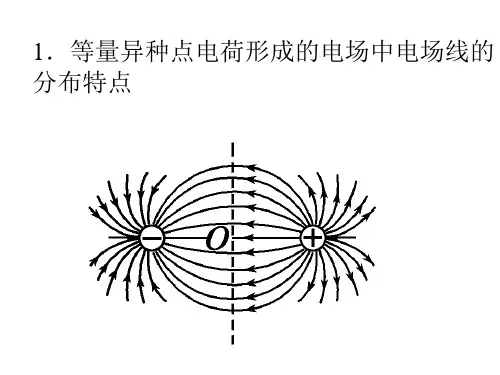
一．等量异种点电荷形成的电场中电场线的分布特点1.两点电荷连线上各点，电场线方向从正电荷指向负电荷．2.两点电荷连线的中垂面(中垂线)上，电场线方向均相同，即场强方向均相同，且总与中垂面(线)垂直．在中垂面(线)上到O点等距离处各点的场强相等(O为两点电荷连线中点)．3.在中垂面(线)上的电荷受到的静电力的方向总与中垂面(线)垂直，因此，在中垂面(线)上移动电荷时静电力不做功．4.等量异种点电荷连线上以中点O场强最小，中垂线上以中点O的场强为最大；5.等量异种点电荷连线和中垂线上关于中点对称处的场强相同；二.等量同种点电荷形成的电场中电场线的分布特点1.两点电荷连线中点O处场强为零，此处无电场线．2.中点O附近的电场线非常稀疏，但场强并不为零．3.两点电荷连线中垂面(中垂线)上，场强方向总沿面(线)远离O(等量正电荷)．4.在中垂面(线)上从O点到无穷远，电场线先变密后变疏，即场强先变强后变弱．5.等量同种点电荷连线上以中点电场强度最小，等于零．因无限远处场强E∞＝0，则沿中垂线从中点到无限远处，电场强度先增大后减小，之间某位置场强必有最大值．6.等量同种点电荷连线和中垂线上关于中点对称处的场强大小相等、方向相反.等量异种电荷和等量同种电荷连线上以及中垂线上电场强度各有怎样的规律？(1)等量异种点电荷连线上以中点O场强最小，中垂线上以中点O的场强为最大；等量同种点电荷连线上以中点电场强度最小，等于零．因无限远处场强E∞＝0，则沿中垂线从中点到无限远处，电场强度先增大后减小，之间某位置场强必有最大值．(2)等量异种点电荷连线和中垂线上关于中点对称处的场强相同；等量同种点电荷连线和中垂线上关于中点对称处的场强大小相等、方向相反.三．等量异种同种电荷产生电场电势等势面1.等量异种点电荷的电场：是两簇对称曲面，两点电荷连线的中垂面是一个等势面．如图－所示．在从正电荷到负电荷的连线上电势逐渐降低，φA>φA′；在中垂线上φB＝φB′.2.等量同种点电荷的电场：是两簇对称曲面，如图1－4－7所示，在AA′线上O点电势最低；在中垂线上O点电势最高，向两侧电势逐渐降低，A、A′和B、B′对称等势．1．如图所示，在真空中有两个固定的等量异种点电荷+Q 和-Q 。

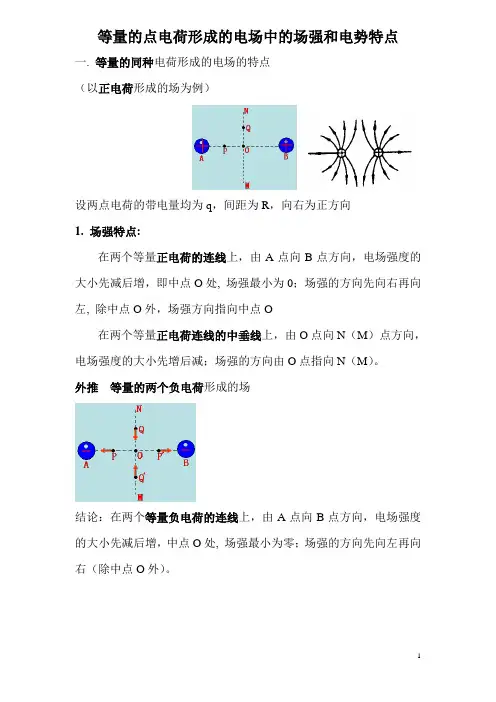
等量的点电荷形成的电场中的场强和电势特点一. 等量的同种电荷形成的电场的特点（以正电荷形成的场为例）设两点电荷的带电量均为q，间距为R，向右为正方向1.场强特点:在两个等量正电荷的连线上，由A点向B点方向，电场强度的大小先减后增，即中点O处, 场强最小为0；场强的方向先向右再向左, 除中点O外，场强方向指向中点O在两个等量正电荷连线的中垂线上，由O点向N（M）点方向，电场强度的大小先增后减；场强的方向由O点指向N（M）。

外推等量的两个负电荷形成的场结论：在两个等量负电荷的连线上，由A点向B点方向，电场强度的大小先减后增，中点O处, 场强最小为零；场强的方向先向左再向右（除中点O外）。

在等量负电荷的连线的中垂线上，由O点向N（M）点方向，电场强度的大小先增后减，场强的方向由N（M）指向O点2.电势特点:在两个等量正电荷的连线上，由A点向B点方向，电势先减后增，中点O处, 电势最小，但电势总为正。

在两个等量正电荷的连线的中垂线上，由O点向N（M）点方向，电势一直减小且大于零，即O点最大，N(M)点为零外推等量的两个负电荷形成的场在两个等量负电荷连线上，由A点向B点方向，电势先增后减，在中点O处, 电势最大但电势总为负；在两个等量负电荷连线的中垂线上，由O点向N（M）点方向，电势一直增大且小于零，即O点最小，N(M)点为零二：等量的异种电荷形成的电场的特点1.场强特点在两个等量异种电荷的连线上，由A点向B点方向，电场强度的大小先减小后增大，中点O处场强最小；场强的方向指向负电荷在两个等量异种电荷的连线的中垂线上，由O点向N（M）点方向，电场强度的大小一直在减小；场强的方向平行于AB连线指向负电荷一端2.电势特点:在两个等量异种电荷的连线上，由A点向B点方向，电势一直在减小，中点O处电势为零，正电荷一侧为正势，负电荷一侧为负势。

等量异种电荷连线的中垂线上任意一点电势均为零即等量异种电荷的连线的中垂线（面）是零势线（面）库仑定律内容表述：真空中两个静止点电荷之间的相互作用力的大小跟两个点电荷的电荷量的乘积成正比，跟它们的距离的二次方成反比．作用力的方向在两个点电荷的连线上公式： 静电力常量：k = 9.0×109 N·m2/C2库仑定律适用条件：真空中，点电荷点电荷——理想化模型，实际上是不存在的．但只要带电体本身的大小跟它们之间的距离相比可以忽略，带电体就可以看作点电荷．并非是体积小就能当点电荷（理想化研究方法）启示与小结：可以看出，万有引力公式和库仑定律公式在表面上很相似，只有质量和电荷量的区别，体现了科学的一种对称美，它们的实质区别是：首先万有引力公式计算出的力只能是相互吸引的力，绝没有相排斥的力．其次，由计算结果看出，电子和质子间的万有引力比它们之间的静电引力小的很多，因此在研究微观带电粒子间的相互作用时，主要考虑静电力，万有引力虽然存在，但相比之下非常小，所以可忽略不计电场：是力的作用媒介：电荷之间的相互作用是通过特殊形式的物质——电场发生的，电荷的周围都存在电场，电场的物质性是客观存在的，具有物质的基本属性——质量和能量。