凸轮廓线解析法
- 格式:doc
- 大小:468.00 KB
- 文档页数:3

第三节 盘形凸轮廓线的设计当根据工作要求和结构条件选定了凸轮机构的类型、从动件的运动规律和凸轮的基圆半径(其确定将在下节中介绍)等结构参数后,就可以设计凸轮的轮廓曲线。
凸轮廓线的设计方法有图解法和解析法,其设计原理基本相同。
本节先简要介绍图解法,后重点介绍解析法设计凸轮廓线。
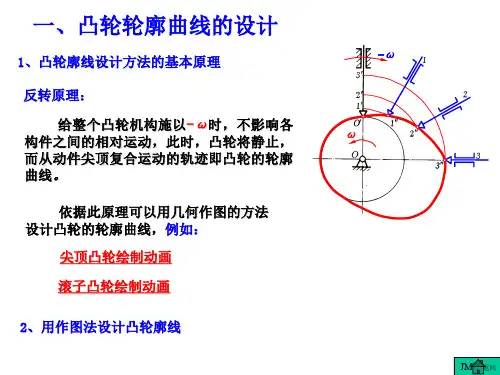
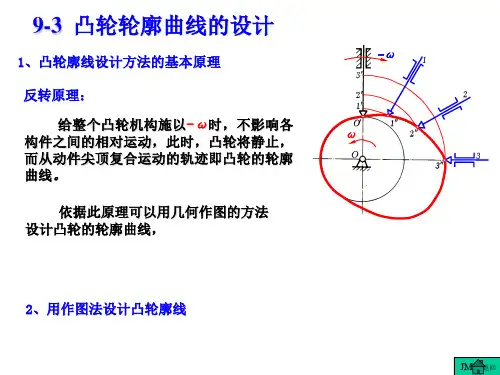
一、凸轮廓线设计的基本原理图4-13 反转法设计凸轮廓线基本原理图4-13所示为一尖顶对心盘形凸轮机构,设凸轮以等角速度ω逆时针转动,推动从动件2在导路中上、下往复移动。
当从动件处于最低位置时,凸轮轮廓曲线与从动件在A 点接触,当凸轮转过1ϕ角时,凸轮的向径A A 0将转到A A '0位置,而凸轮轮廓将转到图中虚线所示的位置。
从动件尖端从最低位置A 上升至B ',上升的位移为B A S '=1,这是从动件的运动位移。
若设凸轮不动,从动件及其运动的导路一起绕A 0点以等角速度-ω转过1ϕ角,从动件将随导路一起以角速度-ω转动,同时又在导路中作相对导路的移动,如图中的虚线位置,此时从动件向上移动的位移为B A 1。
而且,11S B A B A ='=,即在上述两种情况下,从动件移动的距离不变。
由于从动件尖端在运动过程中始终与凸轮轮廓曲线保持接触,所以从动件尖端的运动轨迹即为凸轮轮廓。
设计凸轮廓线时,可由从动件运动位移先定出一系列的B 点,将其连接成光滑曲线,即为凸轮廓线。
由于这种方法是假设凸轮固定不动而使从动件连同导路一起反转,故称为反转法。
对其它类型的凸轮机构,也可利用反转法进行分析和凸轮廓线设计。
二、图解法设计凸轮廓线1. 移动从动件盘形凸轮廓线的设计(1)尖端从动件 图4-14a 所示为一偏置移动尖端从动件盘形凸轮机构。
设已知凸轮的基圆半径为b r ,从动件导路偏于凸轮轴心A 0的左侧,偏距为e ,凸轮以等角速度ω顺时针方向转动。
从动件的位移曲线如图4-14b 所示,试设计凸轮的轮廓曲线。
图4-14 尖端从动件盘形凸轮廓线设计依据反转法原理,具体设计步骤如下。

所属标签:产品外观设计根据使用要求确定了凸轮机构的类型、基本参数以及从动件运动规律后,即可进行凸轮轮廓曲线的设计。
设计方法有几何法和解析法,两者所依据的设计原理基本相同。
几何法简便、直观,但作图误差较大,难以获得凸轮轮廓曲线上各点的精确坐标,所以按几何法所得轮廓数据加工的凸轮只能应用于低速或不重要的场合。
对于高速凸轮或精确度要求较高的凸轮,必须建立凸轮理论轮廓曲线、实际轮廓曲线以及加工刀具中心轨迹的坐标方程,并精确地计算出凸轮轮廓曲线或刀具运动轨迹上各点的坐标值,以适合在数控机床上加工。
圆柱凸轮的廓线虽属空间曲线,但由于圆柱面可展成平面,所以也可以借用平面盘形凸轮轮廓曲线的设计方法设计圆柱凸轮的展开轮廓。
下面时间财富网的小编分别介绍用几何法和解析法设计凸轮轮廓曲线的原理和步骤。
1 几何法反转法设计原理:以尖底偏置直动从动件盘形凸轮机构为例:凸轮机构工作时,凸轮和从动件都在运动。
为了在图纸上画出凸轮轮廓曲线,应当使凸轮与图纸平面相对静止,为此,可采用如下的反转法:使整个机构以角速度(-w)绕O转动,其结果是从动件与凸轮的相对运动并不改变,但凸轮固定不动,机架和从动件一方面以角速度(-w)绕O转动,同时从动件又以原有运动规律相对机架往复运动。
根据这种关系,不难求出一系列从动件尖底的位置。
由于尖底始终与凸轮轮廓接触,所以反转后尖底的运动轨迹就是凸轮轮廓曲线。
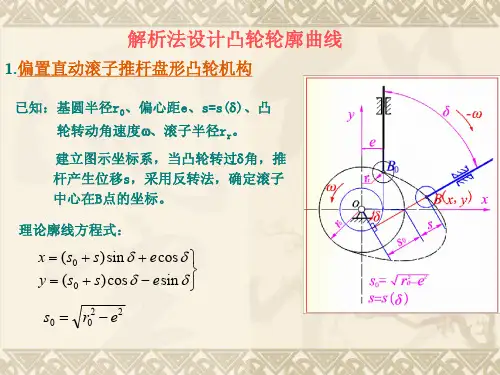
1). 直动从动件盘形凸轮机构尖底偏置直动从动件盘形凸轮机构:已知从动件位移线图,凸轮以等角速w顺时针回转,其基圆半径为r0,从动件导路偏距为e,要求绘出此凸轮的轮廓曲线。
运用反转法绘制尖底直动从动件盘形凸轮机构凸轮轮廓曲线的方法和步骤如下:1) 以r0为半径作基圆,以e为半径作偏距圆,点K为从动件导路线与偏距圆的切点,导路线与基圆的交点B0(C0)便是从动件尖底的初始位置。
2) 将位移线图s-f的推程运动角和回程运动角分别作若干等分(图中各为四等分)。

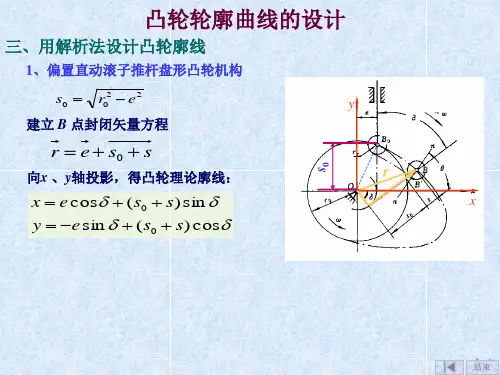



凸轮解析法设计预备知识:坐标旋转cos sin 'sin cos 'x x y y αααα-⎛⎫⎡⎤⎛⎫= ⎪ ⎪⎢⎥⎝⎭⎣⎦⎝⎭问题1:对心尖顶盘状凸轮00''x r s y ⎛⎫⎛⎫= ⎪ ⎪+⎝⎭⎝⎭问题2:偏置尖顶盘状凸轮''e x y s ⎛⎫⎛⎫=⎪ ⎪⎪⎝⎭⎭问题3:摆动尖顶盘状凸轮32020cos()'sin()'l l x l y ϕϕϕϕ-+⎛⎫⎛⎫= ⎪ ⎪+⎝⎭⎝⎭问题4:平底直动盘状凸轮12120',/'oP x oP v r s y ω⎛⎫⎛⎫== ⎪ ⎪+⎝⎭⎝⎭问题5:滚子直动盘状凸轮 包络线方程(,,)00f x y f θθ=⎧⎪∂⎨=⎪∂⎩ 1)222()()0T x X y Y r -+--=(理论廓线任一点(x ,y )为圆心的滚子上必有一点属于工作廓线,即(X ,Y ))2)()()0dx dy x X y Y d d ϕϕ-+-=T X x r =±,(/T Y y r dx =练习1:4-10练习2:(10分)图示凸轮机构中凸轮是一偏心圆盘,该圆盘几何中心为A,半径e=,图示位置从动杆垂直AO,主动件凸轮转向R=,偏心距40mm100mm如图所示。
在图中标出从动件位移最大的位置,并计算出最大位移?h=及推程角?Φ=(注意:图形应画在答题纸上,不要直接画在题签上。
)练习3:4、(10分)一偏置直动尖项从动件盘形凸轮机构如图所示。
已知凸轮为一偏心圆盘,圆盘半径30mmR=,几何中心为A,回转中心为O,从动件偏距OA=。
凸轮以等角速度ω逆时针方向转动。
当凸轮在图==,10mmOD e10mm示位置,即AD CD⊥时,试求:r;(2)图示位置的凸轮机构压力角α;(1)凸轮的基圆半径(3)图示位置的凸轮转角ϕ;(4)图示位置的从动件的位移s;(5)该凸轮机构中的从动件偏置方向是否合理,为什么?3、(10分)图示凸轮机构的实际廓线是一偏心圆盘,该圆盘几何中心为A ,半径100mm R =,偏心距40mm e =,滚子半径10mm T r =,图示位置从动杆垂直AO ,主动件凸轮转向如图所示。
凸轮解析法设计
预备知识:坐标旋转
cos sin 'sin cos 'x x y y αααα-⎛⎫⎡⎤⎛⎫= ⎪ ⎪⎢⎥⎝⎭⎣⎦⎝⎭
问题1:对心尖顶盘状凸轮
00''x r s y ⎛⎫⎛⎫= ⎪ ⎪+⎝⎭⎝⎭
问题2:偏置尖顶盘状凸轮
''e x y s ⎛⎫⎛⎫=⎪ ⎪⎪⎝⎭⎭
问题3:摆动尖顶盘状凸轮
32020cos()'sin()'l l x l y ϕϕϕϕ-+⎛⎫⎛⎫= ⎪ ⎪+⎝⎭⎝⎭
问题4:平底直动盘状凸轮
12120',/'oP x oP v r s y ω⎛⎫⎛⎫== ⎪ ⎪+⎝⎭⎝⎭
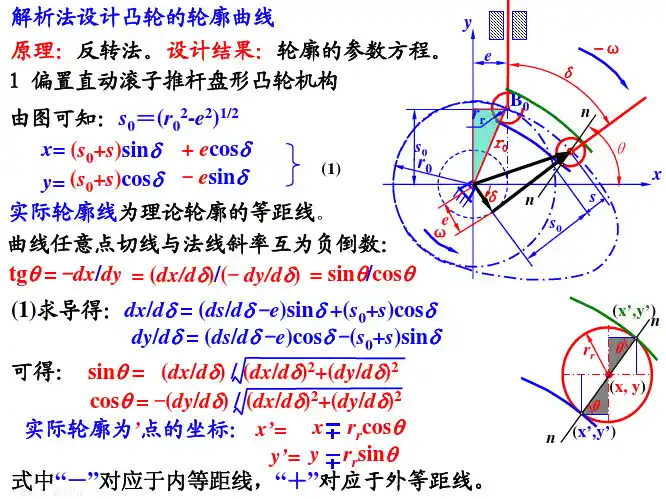
问题5:滚子直动盘状凸轮 包络线方程(,,)0
0f x y f θθ
=⎧⎪∂⎨=⎪∂⎩ 1)222()()0T x X y Y r -+--=(理论廓线任一点(x ,y )为圆心的滚子上必有一点属于工作廓线,即(X ,Y ))
2)()
()0dx dy x X y Y d d ϕϕ-+-=
T X x r =±,(/T Y y r dx =
练习1:4-10
练习2:
(10分)图示凸轮机构中凸轮是一偏心圆盘,该圆盘几何中心为A,半径
e=,图示位置从动杆垂直AO,主动件凸轮转向R=,偏心距40mm
100mm
如图所示。
在图中标出从动件位移最大的位置,并计算出最大位移?
h=及推程角?
Φ=(注意:图形应画在答题纸上,不要直接画在题签上。
)
练习3:
4、(10分)一偏置直动尖项从动件盘形凸轮机构如图所示。
已知凸轮为一偏心圆盘,圆盘半径30mm
R=,几何中心为A,回转中心为O,从动件偏距
OA=。
凸轮以等角速度ω逆时针方向转动。
当凸轮在图==,10mm
OD e
10mm
示位置,即AD CD
⊥时,试求:
r;(2)图示位置的凸轮机构压力角α;
(1)凸轮的基圆半径
(3)图示位置的凸轮转角ϕ;(4)图示位置的从动件的位移s;
(5)该凸轮机构中的从动件偏置方向是否合理,为什么?
3、(10分)图示凸轮机构的实际廓线是一偏心圆盘,该圆盘几何中心为A ,半
径100mm R =,偏心距40mm e =,滚子半径10mm T r =,图示位置从动杆垂直AO ,主动件凸轮转向如图所示。
在图中标出从动件位移最大的位置,并计算出最大位移?h =及推程角?Φ=(注意:图形应画在答题纸上,不要直接画在题签上。
)
e
A
O
ω
R
图示为一偏置直动滚子从动件盘形凸轮机构,凸轮为偏心圆盘。
其直径
D =42mm ,滚子半径 r r =5 mm ,偏距 e =6 mm ,试:
(1)确定基圆半径,并画出基圆;
(2)画出凸轮的理论轮廓曲线;
(3)求出从动件的行程 h ;
(4)确定从动件的推程运动角Φ及回程运动角Φ';
(5)说明该机构在运动中有无失真现象,为什么?。