一、凸轮廓线设计的基本原理

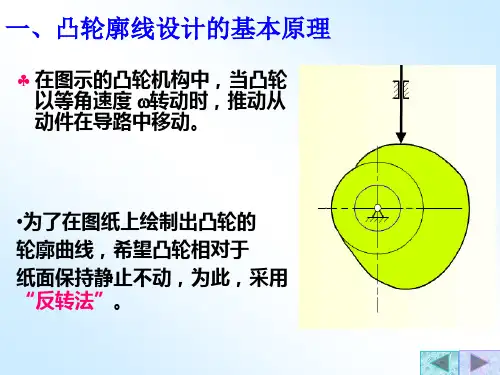
第三节 盘形凸轮廓线的设计当根据工作要求和结构条件选定了凸轮机构的类型、从动件的运动规律和凸轮的基圆半径（其确定将在下节中介绍）等结构参数后，就可以设计凸轮的轮廓曲线。

凸轮廓线的设计方法有图解法和解析法，其设计原理基本相同。

本节先简要介绍图解法，后重点介绍解析法设计凸轮廓线。

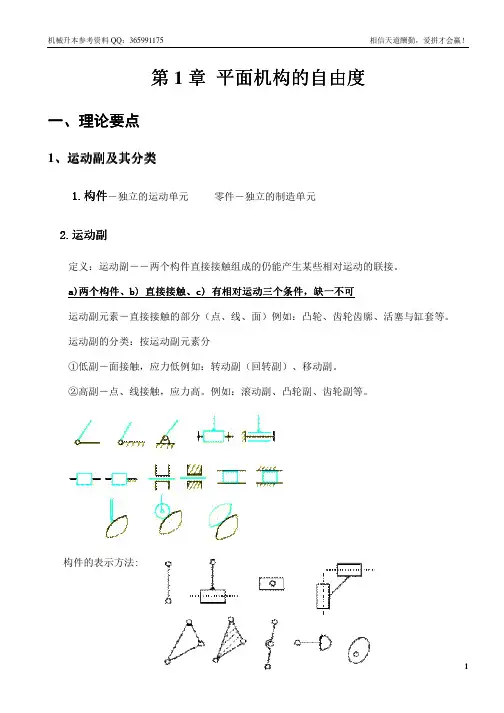
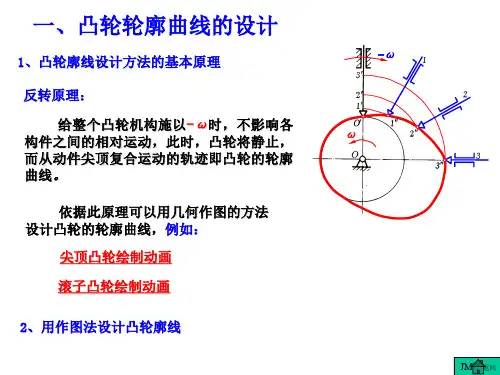
一、凸轮廓线设计的基本原理图4-13 反转法设计凸轮廓线基本原理图4-13所示为一尖顶对心盘形凸轮机构，设凸轮以等角速度ω逆时针转动，推动从动件2在导路中上、下往复移动。

当从动件处于最低位置时，凸轮轮廓曲线与从动件在A 点接触，当凸轮转过1ϕ角时，凸轮的向径A A 0将转到A A '0位置，而凸轮轮廓将转到图中虚线所示的位置。

从动件尖端从最低位置A 上升至B '，上升的位移为B A S '=1，这是从动件的运动位移。

若设凸轮不动，从动件及其运动的导路一起绕A 0点以等角速度-ω转过1ϕ角，从动件将随导路一起以角速度-ω转动，同时又在导路中作相对导路的移动，如图中的虚线位置，此时从动件向上移动的位移为B A 1。

而且，11S B A B A ='=，即在上述两种情况下，从动件移动的距离不变。

由于从动件尖端在运动过程中始终与凸轮轮廓曲线保持接触，所以从动件尖端的运动轨迹即为凸轮轮廓。

设计凸轮廓线时，可由从动件运动位移先定出一系列的B 点，将其连接成光滑曲线，即为凸轮廓线。

由于这种方法是假设凸轮固定不动而使从动件连同导路一起反转，故称为反转法。

对其它类型的凸轮机构，也可利用反转法进行分析和凸轮廓线设计。

二、图解法设计凸轮廓线1. 移动从动件盘形凸轮廓线的设计（1）尖端从动件 图4-14a 所示为一偏置移动尖端从动件盘形凸轮机构。

设已知凸轮的基圆半径为b r ，从动件导路偏于凸轮轴心A 0的左侧，偏距为e ，凸轮以等角速度ω顺时针方向转动。

从动件的位移曲线如图4-14b 所示，试设计凸轮的轮廓曲线。

图4-14 尖端从动件盘形凸轮廓线设计依据反转法原理，具体设计步骤如下。

第六讲凸轮机构及其设计（一）凸机构的用和分一、凸机构1．成：凸，推杆，机架。

2．点：只要合适地出凸的廓曲，就可以使推杆获取各种期的运律，而且机构凑。

缺点：凸廓与推杆之点、接触，易磨，所以凸机构多用在力不大的合。

二、凸机构的分1．按凸的形状分：形凸柱凸2．按推杆的形状分尖推杆：构，能与复的凸廓保持接触，任意期运。

易遭磨，只适用于作用力不大和速度低的合子推杆：摩擦力小，承力大，可用于大的力。

不能够与凹槽的凸廓保持接触。

平底推杆：不考摩擦，凸推杆的作用力与从件平底垂直，受力平；易形成油膜，滑好；效率高。

不能够与凹槽的凸廓保持接触。

3．按从件的运形式分（1）往来直运：直推杆，又有心和独爱式两种。

（ 2）往来运：推杆，也有心和独爱式两种。

4．依照凸与推杆接触方法不同样分：（1）力封的凸机构：通其他外力（如重力，性力）使推杆始与凸保持接触，（ 2）几何形状封的凸机构：利用凸或推杆的特别几何构使凸与推杆始保持接触。

①等凸机构②等径凸机构③共凸（二）推杆的运动规律一、基本名：以凸的回心O 心，以凸的最小半径r0半径所作的称凸的基，r 0称基半径。

推程：当凸以角速度，推杆被推到距凸中心最的地址的程称推程。

推杆上升的最大距离称推杆的行程，相的凸角称推程运角。

回程：推杆由最位置回到初步地址的程称回程，的凸角称回程运角。

休止：推杆于静止不的段。

推杆在最静止不，的凸角称休止角；推杆在近来静止不，的凸角称近休止角二、推杆常用的运律1．性冲：推杆在运开始和止，速度突，加速度在理大将出瞬的无大，致使推杆生特别大的性力，所以使凸碰到极大冲，种冲叫性冲。

2.柔性冲：加速度有突，所以推杆的性力也将有突，不一突有限，所以引起有限冲，叫柔性冲。

3.掌握等速运律和等加速等减速运律的推程的速度、位移、加速度的方程：推杆运律——推杆在推程或回程，其位移s、速度 v 和加速度 a 随t 化的律。

3.1 多式运律：一般表示：s = C0+ C1δ+ C2δ2+⋯ + C nδn（ 1）一次多式运律（等速运律）δδν推程：s=hδ/ δ0v = hω/δ0δa =0δ/ωh＋∞δ－∞图7-7回程： s=h(1- δ / δˊ )v=- hδ ˊ0ω/图示为其推程运动线图。

二、用图解法设计凸轮轮廓曲线 下面以偏置尖顶直动从动件盘形凸轮机构为例，讲解凸轮廓线的设计过程。

例6-1 对心直动尖顶从动件盘形凸轮机构设已确定基圆半径mm 150=r ，凸轮顺时针方向匀速转动，从动件行程mm 18=h 。

从动件运动规律如下表所示：推程 远休止 回程 近休止运动角1120δ=260δ=903=δ490δ=从动件运动规律等速运动正弦加速度运动设计步骤：1、建立推程段的位移方程：18120s δ=，回程段的位移方程：12π181sin 902π90s δδ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦，将推程运动角、回程运动角按某一分度值等分成若干份，并求得对应点的位移。

2、画基圆和从动件的导路位置3、画反转过程中从动件的各导路位置4、画从动件尖顶在复合运动中的各个位置点5、分别将推程段和回程段尖顶的各位置点连成光滑曲线，再画出远休止段和近休止段的圆弧，即完成了尖顶从动件盘形凸轮轮廓曲线的设计，如图6-18。

需要注意：同一个图上作图比例尺必须一致。

如各分点的位移与基圆应按相同比例尺量取。

2．偏置直动尖顶从动件盘形凸轮机构凸轮转动中心O 到从动件导路的垂直距离e 称为偏距。

以O 为圆心，e 为半径所作的圆称为偏距圆。

显然，从动件导路与偏距圆相切（图中K 为从动件初始位置与基圆的切点）。

在反转过程中，从动件导路必是偏距圆的切线。

如图6-19。

r0a A0A1OB0B1内 容3．直动滚子从动件盘形凸轮机构例题：已知：r r －滚子半径，0r －基圆半径，从动件运动规律。

设计该机构。

设计思路：把滚子中心看作尖顶从动件的尖顶，按前述方法先画出滚子中心所在的廓线——凸轮的理论廓线。

再以理论廓线上各点为圆心，以滚子半径r r 为半径画一系列的圆，这些圆的内包络线 即为凸轮的实际廓线（或称为工作廓线）。

如图6-16 注意：滚子从动件盘形凸轮的基圆半径是指其理论廓线的最小向径4．对心直动平底从动件盘形凸轮机构思路：把平底与导路的交点Ａ看作尖顶从动件的尖点，依次作出交点的位置，通过这些位置点画出从动件平底的各个位置线，然后作这些平底的包络线，即为凸轮的工作廓线，如图6-17图6-16图6-17图6-18图6-19内 容5．摆动尖顶从动件盘形凸轮机构已知：基圆半径0r ，摆动从动件的杆长为L （从尖点到从动件回转中心的距离），凸轮回转中心到从动件回转中心的距离a 。

机械原理大作业凸轮凸轮是一种常见的机械传动装置，通过其特殊的轮廓形状和旋转运动，可以实现对连杆机构的运动控制。

在机械原理的学习中，凸轮是一个重要的研究对象，其设计和运用涉及到机械工程、动力学、运动学等多个学科领域。

本文将从凸轮的基本原理、结构特点、工作原理和应用范围等方面进行介绍和分析。

首先，凸轮的基本原理是利用凸轮轮廓的不规则形状，在旋转运动中对连杆机构施加不同的力和运动规律，从而实现对机械装置的运动控制。

凸轮的轮廓可以是圆形、椭圆形、心形等多种形状，根据具体的运动要求和传动方式来设计选择。

凸轮的轮廓形状决定了其在运动中对连杆机构的推动和拉动效果，是凸轮传动的关键。

其次，凸轮的结构特点主要包括凸轮轴、凸轮轮廓和凸轮支撑等部分。

凸轮轴是凸轮的轴心部分，通过轴承和传动装置与动力源相连，实现旋转运动。

凸轮轮廓是凸轮的轮廓外形，根据具体的运动要求和传动方式进行设计和加工。

凸轮支撑是凸轮的固定支撑装置，通常由轴承、轴套和固定座等部分组成，用于支撑和固定凸轮的运动。

凸轮的工作原理是利用凸轮轮廓的不规则形状，在旋转运动中对连杆机构施加不同的力和运动规律，从而实现对机械装置的运动控制。

当凸轮轴转动时，凸轮轮廓与连杆机构发生接触和相互作用，通过凸轮的推动和拉动作用，实现对连杆机构的运动控制。

凸轮的工作原理是基于凸轮轮廓的不规则形状和旋转运动，通过对连杆机构施加不同的力和运动规律，实现对机械装置的运动控制。

最后，凸轮在机械工程中有着广泛的应用范围，常见的应用包括发动机气门控制、机床加工控制、自动化生产线等领域。

在发动机气门控制中，凸轮通过其特殊的轮廓形状和旋转运动，实现对气门的开启和关闭，从而控制气缸内气体的进出。

在机床加工控制中，凸轮通过其特殊的轮廓形状和旋转运动，实现对工件的加工和定位，从而实现精密加工和高效生产。

在自动化生产线中，凸轮通过其特殊的轮廓形状和旋转运动，实现对工件的输送和定位，从而实现自动化生产和装配。