投入产出模型2人大夏明老师主讲

爱考机构 中国高端考研第一品牌（保过保录限额）爱考机构-人大考研-经济学院研究生导师简介-夏明
姓名：夏明
职称/职务:副教授
办公电话:82500717
E-mail:xiamgruc@
研究领域:投入产出分析
来校时间:1992
教育背景
1992年于安徽大学经济管理系国民经济计划学专业取得学士学位，毕业后在安徽省芜湖县计划委员会从事经济计划工作。

1994年考入中国人民大学国民经济管理系，师从我国投入产出专家刘起运教授开始研究生学习，分别于1997与2000年获得经济学硕士和博士学位，毕业后留校任教。

工作经历
现为中国人民大学国民经济管理系副教授
社会兼职
中国投入产出学会常务理事。

海外讲学经历
2002至2004年经教育部选拔赴日本东京大学进行博士后研究。

论文
《结构化凯恩斯乘数方法的辨析与应用》,夏明,《统计与决策》,2010年第10期
《生产率增长的规模递增效应与经济结构转变——卡尔多—凡登定律对中国经济适用性的检验》,夏明,《经济理论与经济管理》,2007年第1期
《技术转变与资本积累体制——法国调节学派的经济增长理论述评》,夏明,《国外社会科学》,2006年第4期
《转轨以来中国经济结构转变的实证分析》,夏明,《统计研究》,2002年第2期
著作
《投入产出体系与经济结构变迁》，夏明，中国经济出版社，2006年。

系统控制方法——投入产出分析模型及其应用投入产出分析是将研究对象视为黑箱，通过系统的输入与输出分析研究，来判断和了解系统的状态、行为和功能。

具体地讲，它是研究管理系统各个部分间表现为投入与产出相互关系的经济数量分析方法。

在微观管理系统, 所谓投入是指产品生产所需原材料、辅助材料、燃料动力、固定资产折旧和劳动等等；所谓产出是指产品生产的总量及其分配使用方面的数量，如生产消费、外销量及增加储备等等，其中生产消费称为中间产品，外销产品和增加储备称为最终产品。

投入产出分析法最初是由国民经济各个产业部门（工业，农业等）间的联系发展起来的，故称其为部门联系平衡法或产业关联法，但它的应用十分广泛，不仅可应用于国民经济、地区经济的综合平衡，也可以有效地应用于企业内部的综合平衡，尤其适用于产品种类繁多，产品间联系复杂的企业。

在企业中应用投入产出分析通常包括三个步骤：一是编制投入产出表，二是建立投入产出数学模型；三是应用模型进行经济分析或实施优化分析。

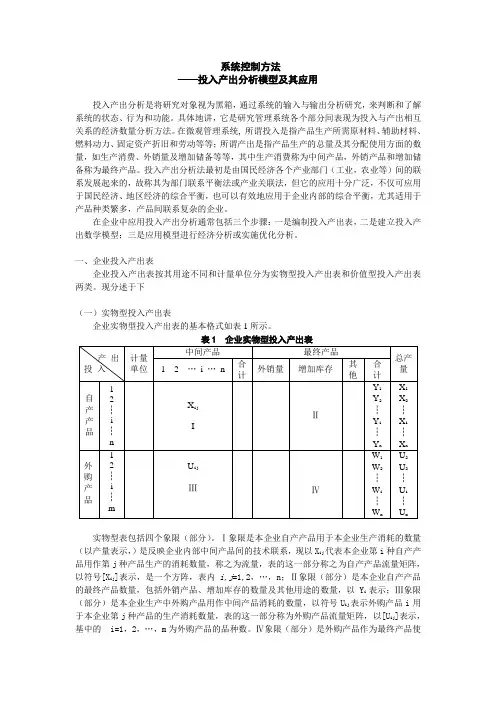
一、企业投入产出表企业投入产出表按其用途不同和计量单位分为实物型投入产出表和价值型投入产出表两类。

现分述于下（一）实物型投入产出表企业实物型投入产出表的基本格式如表1所示。

实物型表包括四个象限（部分）。

Ⅰ象限是本企业自产产品用于本企业生产消耗的数量（以产量表示，）是反映企业内部中间产品间的技术联系，现以X ij代表本企业第i种自产产品用作第j种产品生产的消耗数量，称之为流量，表的这一部分称之为自产产品流量矩阵，以符号[X ij]表示，是一个方阵，表内i,j=1,2，…，n；Ⅱ象限（部分）是本企业自产产品的最终产品数量，包括外销产品、增加库存的数量及其他用途的数量，以Y i表示；Ⅲ象限（部分）是本企业生产中外购产品用作中间产品消耗的数量，以符号U ij表示外购产品i用于本企业第j种产品的生产消耗数量，表的这一部分称为外购产品流量矩阵，以[U ij]表示，基中的i=1，2，…，m为外购产品的品种数。

投入产出模型6.1 投入产出模型投入产出模型对于研究分析国民经济各部门之间的数量依存关系，制定国民经济的计划与规划等都具有十分重要的作用。

根据投入产出模型的原理与方法，现介绍其建模与应用分析的具体方法步骤。

第1节投入产出模型概述投入产出分析是20世纪30年代由美国经济学家瓦。

列昂节夫（W. Leontif）首先提出的，它是研究整个经济系统各部门之间“投入”与“产出”关系的线性模型，一般称为投入产出模型。

国民经济各个部门之间存在着相互依存的关系，每个部门在运转中将其它部门的成品或半成品经过加工（称为投入）变为自己的产品（称为产出），如何根据各部门之间的投入-产出关系，确定各部门的产出水平，以满足社会的需求，是投入产出综合平衡模型研究的问题。

投入产出表投入平衡表简称投入产出表，它是指能够把国民经济各部门之间所有产品的投入与产出关系都表现出来的统计表格。

它是建立投入模型的基础。

主要根据所研究的目的和要求来确定投入产出表的类型。

现以价值型投入产出表为例，如列昂节夫的第一个投入产出表是研究全美国的经济结构的，他编制了全美国十大部门价值型投入产出表。

如表1是一张简化的中国2002年投入产出表，表中国民经济由农业、工业、建筑业、运输邮电业、批零餐饮业和其它服务业6个部门构成，对每个部门有初始投入和总投入，以及外部需求和总产出。

表1中国2002年投入产出表（产值单位：亿元）表中数字均以产值计算，6个部门的横行表示该部门的产品供给各部门生产使用的数量，6个部门的纵列表示该部门生产中消耗的各部门产品的数量。

直接消耗系数直接消耗系数是投入产出应用分析研究最重要的指标。

可在投入产出表的基础上求算直接消耗系数，它可显示出各个部门在生产中的技术经济联系。

如表1中运输邮电部门消耗403亿元工业部门的产品，总产出为1570亿元，于是运输邮电部门的单位产出对工业部门的直接消耗是403/1570=0.257，如此得到的直接小号系数如表2.由于每个部门的总产出等于总投入，计算式将每行数字相应地除以最后一行数字即可。

投入产出模型与经济影响分析投入产出模型是一种常用的经济分析工具，用于评估不同产业之间的相互依赖关系、经济活动的经济效益以及政策干预对经济发展的影响。

本文将介绍投入产出模型的基本原理和应用，并探讨其在经济影响分析中的作用。

一、投入产出模型的基本原理投入产出模型是由经济学家列昂惕夫提出的一种经济分析工具，旨在描述一个经济体系内各个产业之间的投入和产出关系。

其基本原理是将经济系统划分为不同产业部门，通过分析各部门之间的相互影响，揭示产业间的连锁反应和经济发展的关键因素。

在投入产出模型中，经济活动被划分为几个产业部门，例如农业、制造业、建筑业、金融业等。

每个产业部门的产出由该部门自身的投入和其他各部门的投入决定，而投入则包括物质、劳动力和资本等要素。

通过建立投入产出矩阵，可以量化各个部门之间的关系，进而评估经济活动对产业间的影响程度。

二、投入产出模型的应用1. 经济结构调整：投入产出模型可以帮助政府和企业分析不同产业之间的相互依赖关系，评估调整产业结构对整体经济的影响。

通过定量分析不同产业的关联性，可以为产业政策制定者提供决策依据，以达到优化经济结构的目标。

2. 经济政策评估：投入产出模型可用于评估经济政策的经济效益。

例如，政府实施一项新的刺激措施，通过投入产出模型可以分析该措施对各个产业的影响，并进一步估算其对经济增长、就业率和财政收入等方面的影响。

3. 区域发展规划：投入产出模型也可以用于评估区域发展规划的效果。

通过分析不同区域内各个产业部门之间的投入和产出，可以揭示经济活动对区域发展的影响程度，为制定合理的区域发展策略提供参考。

三、投入产出模型在经济影响分析中的作用投入产出模型在经济影响分析中起着重要的作用。

它可以帮助分析人员理解经济活动的复杂性，揭示经济变动对不同产业的影响，并提供决策者制定合理政策的依据。

投入产出模型的分析结果可以显示不同产业间的关联性，从而帮助评估政策的整体效果。

例如，一项投资政策对某个特定产业的增加投入，可能会产生连锁反应，进而带动其他相关产业的发展，从而实现整体经济的增长。

§ 1・5投入产出模型的基本假设和求解条件任何经济数学模型都是都实际经济活动的抽象，都是在若干基本假设下建立的，或者只有在若干基本假设下才能成立。

关键在于所舍弃的是事物的本质方面还是非本质方面。

一、投入产出模型的基本假设投入产出模型是在如下重要假设下建立的。

1.不可替代假设投入产出模型假设一个部门只生产一种产品，而且只采用一种技术生产；同时，一种产品只由一个部门生产。

为什么要作出该假设？实际经济活动是否满足这一假设？2.线性假设投入产出模型假设投入量与产出量是成正比的，比例系数就是直接消耗系数。

为什么要作出该假设？实际经济活动是否满足这一假设？3.系数不变假设投入产出模型假设直接消耗系数在一个周期内是不变的。

为什么要作出该假设？实际经济活动是否满足这一假设？4.关于生产周期的假设投入产出模型假设每个部门的生产经营活动，从生产要素的投入到产出的分配与使用，都在一个周期内完成。

为什么要作出该假设？实际经济活动是否满足这一假设？如何处理？二、投入产出模型的求解条件所谓“投入产出模型的求解条件”，是指投入产出模型能够求解的条件。

1.投入产出模型能够求解的条件投入产出模型X (I A) 1Y能够求解的条件是矩阵(I A )有逆，且逆矩阵的元素不为负。

是从数学和经济意义两方面提出的。

2.价值型投入产出模型求解条件的证明对于价值型投入产出模型，其直接消耗系数满足：n aij 1 j 1,2, ,ni 1即满足：n a 1 a j 1,2, ,ni 1而在矩阵(I A)中，主对角线元素为1 a jj,其它元素为a ij0所以该矩阵是主对角线元素占优势的矩阵。

由线性代数知识可知，I A 0。

所以矩阵(I A)有逆。

又因为对于矩阵(I A),不仅存在ai 1, 而且存在nai 1. 所以有|I A|。

对于矩阵(I A )的逆矩阵：E 由 其分子为矩阵(I A )对应元素的代数余子式作为元素构成的伴随矩阵，而这些代数余子式 都是大于0,所以(I A )的逆矩阵的元素的都大于0。

§1.4 投入产出经济数学模型本节介绍两个最基本的投入产出经济数学模型。

第三章将要介绍的各种复杂的投入产出应用模型，都是这两个最基本的投入产出经济数学模型的扩展。

一、分配方程组和按行建立的模型⒈ 分配方程组对于投入产出表的每一行，不管是价值型还是实物型，都存在如下平衡方程：n i X Y xi i n j ij ,,2,11==+∑= （1.4.1） 可以写成：n i X Y X ai i n j j ij ,,2,11 ==+∑= （1.4.2）这就是分配方程组。

它反映每个部门的总产出是如何分配与使用的。

用矩阵表示该方程组，有X Y AX =+ （1.4.3） 其中⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nn n n n n a a a a a a a a a 212222111211A ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n Y Y Y 21Y ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n X X X 21X 分别为直接消耗系数矩阵、最终使用量矩阵和总产出量矩阵。

⒉ 按行建立的经济数学模型⑴ 模型形式由（1.4.3），容易得到：Y A I X 1)(--= （1.4.4） 这就是按行建立的投入产出基本经济数学模型。

⑵ 模型的经济意义该模型揭示了最终使用量和总产出量之间的关系。

换句话说，如果知道最终使用量，通过模型就可以求出既满足最终使用的需求、又保证经济系统各部分之间综合平衡的总产出量。

这里的最终使用量就是支出法计算的国内生产总值。

⑶ 模型的应用价值该模型虽然简单，但具有很大的应用价值。

因为在投入产出分析出现以前，还没有什么方法能够揭示最终使用量和总产出量之间的关系。

而这个关系对于经济预测、经济计划、结构分析等无疑是不可缺少的。

⑷ 模型与完全消耗系数的联系所谓最终使用量和总产出量之间的关系，实际上就是完全消耗关系。

将（1.4.4）中Y 前的系数矩阵1)(--A I 与完全消耗系数矩阵I A I B --=-1)(比较，二者仅相差一个单位阵。

投入产出模型第9章投入产出模型投入产出模型对于研究分析国民经济各部门之间的数量依存关系，制定国民经济的计划与规划等都具有十分重要的作用。

根据投入产出模型的原理与方法，现介绍其建模与应用分析的具体方法步骤。

第1节投入产出模型概述1.1 概念投入产出模型是指在马克思主义经济理论指导下，利用数学方法和电子计算机技术，来研究各种经济活动的投入与产出之间的数量依存关系，特别是研究与分析国民经济各个部门在产品的生产与消耗之间的数量依存关系所建立的一种数学模型，其主要含义如下：1）投入产出模型的指导思想是马克思主义经济理论；2）投入产出模型的理论基础是计量经济学理论，集中体现在投入产出方法的原理与方法；3）投入产出模型的关键任务是直接消耗系数与列昂节夫逆矩阵的求算；4）投入产出模型的主要方法是数学方法与计算机技术的应用，集中体现在投入产出模型数学模型的建立及运用计算机进行矩阵运算的求解应用；5）投入产出模型的最终目的是研究与分析各个经济部门之间的数量依存关系，为社会主义经济建设中的科学决策服务。

主要用途是用于研究与分析国民经济各个部门在产品的生产与消耗之间的数量依存关系，反映各个部门之间的直接与间接的经济联系及各个部门之间的综合平衡问题。

目前，已拓展到用于研究与分析各个地区，各个企业内部及之间的各种经济联系。

1.2 作用1）编制国民经济计划。

2）经济指标的预测。

3）经济政策研究，研究重要经济政策对经济建设的影响。

4）专题研究，研究专门的社会经济问题。

5）编制区际经济计划。

1.3 发展概况投入产出法产生于20世纪30年代，是由俄国出生的美国经济学家瓦。

列昂节夫（w. Leontif）首先提出于1931年开始研究“投入产出分析法”，来分析研究美国的经济结构，随后发表了不少的论文和论著，在1944年他编制了美国经济部门的1939年投入产出表，它可称是世界上第一个“投入产出表”，当时，引起了美国政府的重视，此后，美国先后又编制了1947年，1958年，1963年，和1966年的投入产出表。

投入产出模型投入产出模型是指对于经济系统（这一经济系统可以是一个国家，一个地区，一个行业或一个企业的经济活动）的多部门的投入与产出进行研究，编制投入产出表，并建立其数学模型，称作投入产出模型。

这种将经济系统的投入产出关系编制成投入产出表，建立投入产出模型进行研究的方法叫做投入产出法。

投入产出法是由美国著名经济学家瓦西里·列昂节夫20世纪30年代首先提出的。

最初是由研究一国的国民经济各个产业部门间的联系发展起来的,因此被人们称作部门联系平衡法,又叫产业关联法。

利用投入产出模型对经济活动进行分析和进行经济预测，这是一种重要的经济数量分析，叫做投入产出分析。

投入产出分析的理论基础是第七章我们所介绍的一般均衡理论，主要是对一个国家或一个地区宏观经济的研究。

但随着这一方法的广泛应用，它也可以研究一个部门（行业）的经济活动，一个公司或企业的生产经营活动。

本章将在介绍投入产出模型的基础上，着重介绍投入产出模型在国民经济预测和企业经济预测方面的应用。

第一节投入产出模型的基本形式一、投入产出表所谓投入，是指产品生产所需原材料、辅助材料、燃料、动力、固定资产折旧和劳动力的投入；所谓产出，是指产品生产的总量及其分配使用的方向和数量，包括生产消费（中间产品）、生活消费、积累和净出口等。

生产过程就是投入与产出关系的客观反映，一定时期内产品的产出受投入的影响。

投入与产出的数量关系可以编制成一种矩形的表格表示，即投入产出表。

投入产出表可以按实物形态编制，也可以按价值形态编制。

按实物形态编制的投入产出表叫实物表，按价值形态编制的投入产出表叫价值表，两者基本结构形式是相同的，它们之间只差一个价格因素。

投入产出表按编制的范围不同，可以分作世界投入产出表、国家投入产出表、地区投入产出表、部门投入产出表和企业投入产出表。

这里仅以价值形态的全国表为例介绍投入产出表的结构。

假设把国民经济划分为n 个部分，用1，2，…，n 等号码表示。

§3.6 企业投入产出模型一、企业投入产出表对于一个部门或一个大中型企业，包括能源工业部门或能源工业企业，生产多种产品，一部分作为企业（或部门）的最终产品，一部分在企业（或部门）内部生产过程中作为中间产品被消耗，多种产品间也存在着复杂的联系。

一般讲，在计划经济下，国家对该企业（或部门）下达一定的销售指标，给予该企业（或部门）一定的物资（如能源、原材料等），企业（或部门）如何根据国家下达的销售指标来安排企业（或部门）内部各种产品的生产呢？如何安排各种外购物质（包括能源）的供应呢？如何在保证完成国家任务和国家给定的能源和其它物资限制下最优地安排企业（或部门）的生产呢？投入产出法是解决这些问题的一种好方法。

在市场经济下，企业根据市场需要预测销售指标，同样存在如何根据销售指标来安排企业内部各种产品的生产，如何安排各种外购物质（包括能源）的供应，以及如何在保证满足市场需求下最优地安排企业的生产等问题。

而且在市场经济下，企业内部具有很强的计划性。

所以，企业投入产出模型无论对于计划经济，还是市场经济，都是重要的。

部门是同类企业的集合，下面仅就企业为例加以说明。

表3.6.1为企业投入产出表表式。

表中包括企业内部产品n 种，外购物质m 种。

企业销售产品一般即为企业最终产品，国家或者市场给企业下达的生产任务一般就是销售指标。

用x ij 表示企业在生产第j 种产品过程中直接消耗的第i 种产品的数量，v i 、m j 分别表示生产第j 种产品的劳动报酬和纯收入。

这样，从投入产出表中，可以得到下列系数： j j vj X v a = j ij ij X x a =jj mj X m a =jij ij X w =γa ij 为对本企业产品的直接消耗系数，γij 为对外购物资的直接消耗系数，a vj 为劳动报酬系数，a mj 为纯收入系数。

若企业的销售指标为Y Y Y n 12，，…，，则为完成该销售指标，企业必须安排各种产品的生产量为X X X n 12，，， ，企业必须外购各种物资数量为n W W W ,21 ，，，这里2⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-n n Y Y Y A I X X X 21121)(⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡m m X X X R W W W 2121 其中A 为对本企业产品的直接消耗系数矩阵，R 为对外购物资的直接消耗系数矩阵。