小学数学趣题巧算百题百讲百练综合分册
- 格式:docx
- 大小:3.54 MB
- 文档页数:14

小学数学趣题巧算百题百讲百练--应用题部分怎样运用数学概念及运算意义去解应用题呢?首先是要用数学概念去分析题中的数量关系。
这种分析应该说是全面的、深刻的。
要分析已知数量与已知数量,已知数量与未知数量间的关系。
然后根据运算意义,用式子表示出题中要求的数量,使问题得到解决。
小学生在分析应用题中数量关系时,常常缺少更深的思考,只满足于得出一般的解答方法,这是不够的。
重要的是通过全面的、深刻的分析,综合运用数学概念、运算意义,会寻找巧妙的解法,这对发展小学生观察比较、分析综合、判断推理、想象类比的能力是极为有利的。
牢固而清晰地掌握数学概念、运算意义才能使你去深刻地思考问题。
也要学会一些帮你思考的方法。
比如把题中的条件排列出来,画一画示意图、线段图等,总之,把题中的条件、问题形象化是一种常见的、有效的办法。
它能帮你想得更深刻。
解答应用题最忌讳死背题型、死记解题模式,这样往往束缚了你的手脚。
时间久了,你的思维就僵化了,这对今后的学习极为不利。
例45红花衬衫厂要制做一批衬衫,原计划每天生产400件,60天完成。
实际每天生产的件数是原计划每天生产件数的1.5倍。
完成这批衬衫的制做任务,实际用了多少天?分析与解要求完成这批衬衫的制做任务,实际用了多少天,必须知道这批衬衫的总数和实际每天生产的件数。
已知原计划每天生产400件,60天完成,就可以求出这批衬衫的总数量;又知道实际每天生产的件数是原计划生产件数的1.5倍,就可以求出实际每天生产的件数。
完成这批衬衫的制做任务,实际用的天数是:400某60÷(400某1.5)=24000÷600=40(天)也可以这样想:要生产的衬衫的总数量是一定的,所以,完成这批衬衫制做任务所需要的天数与每天生产衬衫的件数成反比例关系。
由此可得,实际完成这批衬衫制做任务的天数的1.5倍,正好是60天,于是得出制做这批衬衫实际需要的天数是:60÷1.5=40(天)答:完成这批衬衫制做任务,实际用了40天。

小学数学趣题巧算百题百讲百练杂题部分3 小学数学六年级人教版分析与解题中告诉我们,四个数的平均数是17,那么这四个数的和就是17×4=68。
题中问d最大是多少。
要使d最大,那么a就要尽量小。
因为这四个数都是自然数,所以a最小为1。
又因为a比b小5,所以这时b为6。
这样不难求出这时c与d的和是68-1-6=61。
题中又告诉我们,d比c大7,这样就可以求出这时d是61+7/2=34,即d最大是34。
那么d最小是多少呢?题中告诉我们,a比b小5,d比c大7,a、b、c、d四个数之和是68,而68+5+7之和正好是b与d的和的2倍,因此b与d 的和是(68+5+7)÷2=40。
要使d最小,那么a、b、c就要尽量大,而b与c的差应该尽量小,而b与c的差最小是1,这样b与d之差就是1+7=8。
由此得出d最小是:40+8/2=24答:d最大是34,最小是24。
例94一个正方体有六个面,分别用字母A、B、C、D、E、F 表示。
图56是从三个不同角度看到的这个正方体的部分面的字母。
那么这个正方体到底哪个面与哪个面相对?分析与解观察题中给出的三个图,不容易看出哪个面与哪个面相对。
那就换一种思考方法,看看哪个面不对着哪个面,从而得出哪个面与哪个面相对的正确结论。
观察图(1)可知,A面不对着D面、E面;观察图(2)可知,A面不对着B面、F面。
由此得出,A面一定对着C面。
再观察图(2),可以知道,F面不对着A面、B面;观察(3)可以知道,F面不对着C面、D面。
那么F面一定对着E面。
这样剩下的B面一定对着D面。
答:这个正方体的A面对着C面;B面对着D面;E面对着F面。
例95一次乒乓球比赛,共有512名乒乓球运动员参加比赛。
比赛采用淘汰制赛法,两个人赛一场,失败者被淘汰,将不再参加比赛;获胜者进入下轮比赛,如此进行下去,直到决赛出第一名为止。
问这次乒乓球比赛一共要比赛多少场?分析与解如果这样去想,第一轮512名运动员参赛,要赛256场;第二轮256名运动员参赛,要赛128场;……直到决赛出第一名为止,再将各轮比赛场次加起来,计算出一共要比赛多少场。


小学数学趣题巧算百题百讲百练--杂题部分数学网为广大小学生和家长整理的“小学数学趣题巧算百题百讲百练系列”,包括计算、几何、应用题、杂题以及各部分练习题,每部分都有100道精选例题及讲解,以提高广大小学生的综合解题能力。
本篇为杂题部分。
小学生的课外数学活动,包括一些数学竞赛活动,极大地提高了小学生学习数学的兴趣和热情。
通过参加各种数学课外活动,提高了学生思维和探索能力。
杂题中选编的例题,更突出了小学数学知识的综合运用。
有的题涉及一点小学尚未学习的知识,但是学生还是可以理解的,题中介绍的各种解法,小学生应该掌握。
例84 将奇数1、3、5、7、9、……按下表排成五列。
例如,13排在第2行第2列,25排在第4行第4列。
那么1993排在第几行第几列?分析与解首先要算出1993这个数是这列数中的第几个数。
由上表可看出,每行有4个数,而997÷4=249……1。
就是说第997个数是第250行中最小的一个。
偶数行的数是从小到大依次排在第4、3、2、1列的,因此1993这个数排在第250行第 4列。
例85 在自然数中有很多三位数,其中三个数字之和是5的倍数的三位数共有多少个?分析与解要想求出三个数字之和是5的倍数的三位数共有多少个,不妨按从小到大的顺序把这些数写出来:104、109、113、118、122、127、……显然,用这种寻找的方法是可以的,但是太费时间了。
我们可以按下面的思路去思考。
这10个连续的三位数的三个数字之和,也正好是10个连续的自然数。
例如,a=1,b=2,那么上面写出的10个连续的三位数的三个数字之和为3、4、5、6、7、8、9、10、11、12。
其中有而且只有两个三位数的三个数字之和是5的倍数。
从100~999,这些三位数共900个,每10个连续三位数为一个“数段”,一共可以分成90个“数段”。
而每10个连续的三位数中有而且只有2个三位数的三个数字之和是5的倍数,所以在所有的三位数中共有2×90=180个三位数,它们的三个数字和是5的倍数。

小学数学趣题巧算百题百讲百练 --应用题部分练习数学网为广大小学生和家长整理的小学数学趣题巧算百题百讲百练系列,包含计算、几何、应用题、杂题以及各部分练习题,每部分都有100 道优选例题及解说,以提升广大小学生的综合解题能力。
本篇为应用题部分练习。
1.小明看一本书,原计划每日看35 页, 32 天看完。
实质每天比计划多看 5 页,实质用多少天看完?2.修一条路,原计划每日修0.4 千米, 70 天能够修完。
实质每日修的米数是计划的 1.25 倍。
实质用多少天达成?3.绿化队植树,计划8 天达成任务。
实质每日植树240 棵, 7天就达成了所有的植树任务。
实质比计划每日多植树多少棵?4.某街道居委会慰劳军烈属,给他们送去红糖和白糖。
每到一户送去 2 袋红糖和 5 袋白糖,送到最后一户时,红糖正好送完,还剩下10 袋白糖。
已知带去的白糖的袋数是红糖袋数的 3 倍,那么带去的红糖、白糖各多少袋?5.服饰厂要加工一批服饰。
第一车间和第二车间同时加工60天正好达成。
已知第一车间加工的服饰占服饰总数的45%,第二车间每日加工132 件。
第一车间每日加工多少件?6.洗衣机厂计划生产一批洗衣机。
结果9 天恰巧达成了计划的 37.5%。
照这样计算,达成计划还要多少天?7.有一堆煤能够烧120 天。
因为改良烧煤技术,每日节俭用煤 0.25 吨,结果这堆煤烧了 150 天。
这堆煤共有多少吨?牵走7 头黄牛放在水牛群之中,那么这三群牛的头数正好相等。
问奶牛有多少头?9.甲乙两个车间加工一批相同的部件。
假如甲车间先加工35个,而后乙先加工 1 天,而后乙车间再开始加工,经过 5 天后两车间加工的部件数相等。
那么乙车间一天加工多少个部件?10.修路队原计划用240 天修睦一条长91200 米的公路。
实际每日比计12.有 100 千克青草,含水量为 66%,晾晒后含水量降到15%。
这些青草晾晒后重多少千克?13.将一个正方形的一边减少1/5,另一边增添 4 米,获得一个长方形。


小学数学趣题巧算百题百讲百练--杂题部分数学网为广大小学生和家长整理的“小学数学趣题巧算百题百讲百练系列”,包括计算、几何、应用题、杂题以及各部分练习题,每部分都有100道精选例题及讲解,以提高广大小学生的综合解题能力。
本篇为杂题部分。
小学生的课外数学活动,包括一些数学竞赛活动,极大地提高了小学生学习数学的兴趣和热情。
通过参加各种数学课外活动,提高了学生思维和探索能力。
杂题中选编的例题,更突出了小学数学知识的综合运用。
有的题涉及一点小学尚未学习的知识,但是学生还是可以理解的,题中介绍的各种解法,小学生应该掌握。
例84 将奇数1、3、5、7、9、……按下表排成五列。
例如,13排在第2行第2列,25排在第4行第4列。
那么1993排在第几行第几列?分析与解首先要算出1993这个数是这列数中的第几个数。
由上表可看出,每行有4个数,而997÷4=249……1。
就是说第997个数是第250行中最小的一个。
偶数行的数是从小到大依次排在第4、3、2、1列的,因此1993这个数排在第250行第4列。
例85 在自然数中有很多三位数,其中三个数字之和是5的倍数的三位数共有多少个?分析与解要想求出三个数字之和是5的倍数的三位数共有多少个,不妨按从小到大的顺序把这些数写出来:104、109、113、118、122、127、……显然,用这种寻找的方法是可以的,但是太费时间了。
我们可以按下面的思路去思考。
这10个连续的三位数的三个数字之和,也正好是10个连续的自然数。
例如,a=1,b=2,那么上面写出的10个连续的三位数的三个数字之和为3、4、5、6、7、8、9、10、11、12。
其中有而且只有两个三位数的三个数字之和是5的倍数。
从100~999,这些三位数共900个,每10个连续三位数为一个“数段”,一共可以分成90个“数段”。
而每10个连续的三位数中有而且只有2个三位数的三个数字之和是5的倍数,所以在所有的三位数中共有2×90=180个三位数,它们的三个数字和是5的倍数。

小学数学趣题巧算百题百讲百练--应用题部分练习1.小明看一本书,原计划每天看35页,32天看完。
实际每天比计划多看5页,实际用多少天看完?2.修一条路,原计划每天修0.4千米,70天可以修完。
实际每天修的米数是计划的1.25倍。
实际用多少天完成?3.绿化队植树,计划8天完成任务。
实际每天植树240棵,7天就完成了全部的植树任务。
实际比计划每天多植树多少棵?4.某街道居委会慰问军烈属,给他们送去红糖和白糖。
每到一户送去2袋红糖和5袋白糖,送到最后一户时,红糖正好送完,还剩下10袋白糖。
已知带去的白糖的袋数是红糖袋数的3倍,那么带去的红糖、白糖各多少袋?5.服装厂要加工一批服装。
第一车间和第二车间同时加工60天正好完成。
已知第一车间加工的7.150天。
牵走9.10.12.有13.14.24个乙种15.16.17.多少人?18.1/4。
那么19.容器里纯酒精含量为40%。
那么原来容器里的酒精溶液共几升?浓度为百分之几?20.甲、乙、丙三人合抄一份稿件,1小时可以完成。
如果甲、乙二人合抄,要80分钟完成;如果乙、丙二人合抄,要100分钟完成。
如果这份稿件由乙一人独抄,要几小时完成?21.一件工程,甲独做,20天可以完成;乙独做,30天可以完成。
现在两人合做,中间甲休息了3天,乙休息了若干天,结果经过16天才完成。
问乙休息了几天?22.注满一池水,只打开甲管,要8小时;只打开乙管,要12小时;只打开丙管,要15小时。
今开始只打开甲、乙两管,中途关掉甲、乙两管,然后打开丙管,前后共用了10小时才注满一池水。
那么打开丙管注水几小时?23.某工程队承建一项工程,要用12天完成。
如果只让其中的甲、乙两个小队交换一下工作内容,那么全工程就要推迟3天完成;如果让其中甲、乙两个小队交换一下工作内容的同时,也让丙、丁两个小队交换工作内容,仍然可以按期完成全工程。
如果只让丙、丁两个小队交换工作内容,那么可以使全工程提前几天完成?24.甲、乙两队合干一项工程,甲队先独干了6天后,乙队参加和甲队一起干,又过了4天完成了全工程的1/3。

几何部分:小学数学趣题巧算百题百讲百练小学生学习几何初步知识,不仅要掌握一些基本的平面图形和立体图形的性质、特征,还要会求这些平面图形的周长、面积及这些立体图形的表面积、体积,而且还要会综合地、巧妙地运用这些知识来进行计算。
特别是计算一些组合图形的面积时,常常用到割补、剪拼、平移、翻转等办法,使得计算巧妙、简便。
要学会这些方法,应用这些方法。
通过解几何题的训练,更好地培养空间想象力,这对学好小学几何初步知识是极有利的,同时也为将来到中学进一步学习几何知识,打下良好而坚实的基础。
例21 下图中圆O的面积和长方形OABC的面积相等。
已知圆O的周长是9.42厘米,那么长方形OABC的周长是多少厘米?分析与解题中告诉我们,圆O的面积和长方形OABC的面积相等。
我们知道,圆的面积等于π·r·r,而图中圆O的半径恰好是长方形的宽,因此长方形OABC的长正好是π·r,即圆O的周长的一半。
而长方形的周长等于2个长与2个宽的和,也就是圆O的周长与直径的和。
长方形OABC的周长是:9.42+9.42÷3.14=9.42+3=12.42(厘米)答:长方形OABC的周长是12.42厘米。
例22桌面上有一条长80厘米的线段,另外有直径为1厘米、2厘米、3厘米、4厘米、5厘米、8厘米的圆形纸片若干张,现在用这些纸片将桌上线段盖住,并且使所用纸片圆周长总和最短,问这个周长总和是多少厘米?分析与解要想盖住桌上线段,并且使所用纸片圆周长总和最短,那么盖住线段的圆形纸片应该是互不重叠,一个挨一个地排开,这时若干个圆形纸片直径的总和正好是80厘米。
这些圆形纸片周长的总和与直径为80厘米的圆的周长相等,因此盖住桌子上线段的若干个圆形纸片的周长总和是:3.14×80=251.2(厘米)答:这个周长总和是251.2厘米。
例23 图2为三个同心圆形的跑道,跑道宽1米。
某人沿每条圆形跑道的中间(虚线所示)各跑了1圈,共3圈。

小学数学趣题巧算百题百讲百练--杂题部分小学生的课外数学活动,包括一些数学竞赛活动,极大地提高了小学生学习数学的兴趣和热情。
通过参加各种数学课外活动,提高了学生思维和探索能力。
杂题中选编的例题,更突出了小学数学知识的综合运用。
有的题涉及一点小学尚未学习的知识,但是学生还是可以理解的,题中介绍的各种解法,小学生应该掌握。
例84 将奇数1、3、5、7、9、……按下表排成五列。
例如,13排在第2行第2列,25排在第4行第4列。
那么1993排在第几行第几列?分析与解首先要算出1993这个数是这列数中的第几个数。
由上表可看出,每行有4个数,而997÷4=249……1。
就是说第997个数是第250行中最小的一个。
偶数行的数是从小到大依次排在第4、3、2、1列的,因此1993这个数排在第250行第 4列。
例85在自然数中有很多三位数,其中三个数字之和是5的倍数的三位数共有多少个?分析与解要想求出三个数字之和是5的倍数的三位数共有多少个,不妨按从小到大的顺序把这些数写出来:104、109、113、118、122、127、……显然,用这种寻找答案的方法是可以的,但是太费时间了。
我们可以按下面的思路去思考。
这10个连续的三位数的三个数字之和,也正好是10个连续的自然数。
例如,A=1,B=2,那么上面写出的10个连续的三位数的三个数字之和为3、4、5、6、7、8、9、10、11、12。
其中有而且只有两个三位数的三个数字之和是5的倍数。
从100~999,这些三位数共900个,每10个连续三位数为一个“数段”,一共可以分成90个“数段”。
而每10个连续的三位数中有而且只有2个三位数的三个数字之和是5的倍数,所以在所有的三位数中共有 2×90=180个三位数,它们的三个数字和是5的倍数。
答:三位数中三个数字之和是5的倍数的共有180个。
例86 有一串数 1、4、9、16、25、26、49、……它们是按一定的规律排列的。
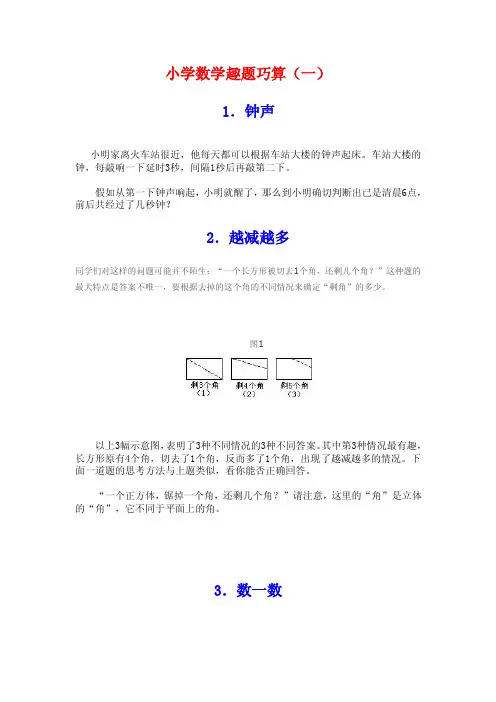
小学数学趣题巧算(一)1.钟声小明家离火车站很近,他每天都可以根据车站大楼的钟声起床。
车站大楼的钟,每敲响一下延时3秒,间隔1秒后再敲第二下。
假如从第一下钟声响起,小明就醒了,那么到小明确切判断出已是清晨6点,前后共经过了几秒钟?2.越减越多同学们对这样的问题可能并不陌生:“一个长方形被切去1个角,还剩几个角?”这种题的最大特点是答案不唯一,要根据去掉的这个角的不同情况来确定“剩角”的多少。
图1以上3幅示意图,表明了3种不同情况的3种不同答案。
其中第3种情况最有趣,长方形原有4个角,切去了1个角,反而多了1个角,出现了越减越多的情况。
下面一道题的思考方法与上题类似,看你能否正确回答。
“一个正方体,锯掉一个角,还剩几个角?”请注意,这里的“角”是立体的“角”,它不同于平面上的角。
3.数一数如果有人问你“会数数儿吗?”,你会不屑一顾地说:“这么大了,还不会数数儿!”其实,数数儿的学问还是很大的。
不信,请你数出下面几何图形的个数。
图24.画一画下面这些图形你能一笔画出来吗?(不重复画)图35.最短的路线养貂专业户养殖场内安置了9个貂笼(如下图)。
为了节省每次喂食的时间,他必须走一条最短的路,但又不能漏掉一个貂笼,喂完食后还要回到原出发点。
你能替他设计一条最短的路线吗?并算出每喂食一次,至少要走多少米的路。
6.切西瓜六(1)班召开夏夜乘凉晚会,买来了许多西瓜。
班主任李老师说:“今天买来了许多西瓜请大家吃。
在吃以前我先要以切西瓜为名请大家做一道数学题。
我规定,西瓜只能竖切,不能横剖。
大家知道,切一刀最多分成2块,切2刀最分成多4块,那么切3刀最多能分成几块?切4刀、切5刀、切6刀呢?这中间有没有规律?如果有规律,请同学们找出来。
”李老师刚说完,同学们就七嘴八舌地讨论起来。
请你也参加他们的讨论吧。
7.均分承包田有一块等腰梯形菜地(如下图),地边有一口水井。
现在3户种菜专业户都提出要承包这块地。
经研究,决定让这3户共同承包这块地,因此必须把这块地分成面积相等、形状相同且与这口水井的距离也要相等的3块地。
小学数学趣题巧算百题百讲百练--杂题部分小学生的课外数学活动,包括一些数学竞赛活动,极大地提高了小学生学习数学的兴趣和热情。
通过参加各种数学课外活动,提高了学生思维和探索能力。
杂题中选编的例题,更突出了小学数学知识的综合运用。
有的题涉及一点小学尚未学习的知识,但是学生还是可以理解的,题中介绍的各种解法,小学生应该掌握。
例84 将奇数1、3、5、7、9、……按下表排成五列。
例如,13排在第2行第2列,25排在第4行第4列。
那么1993排在第几行第几列?分析与解 首先要算出1993这个数是这列数中的第几个数。
分析与解由上表可看出,每行有4个数,而997÷4=249……1。
就是说第997个数是第250行中最小的一个。
偶数行的数是从小到大依次排在第4、3、2、1列的,因此1993这个数排在第250行第 4列。
例85 在自然数中有很多三位数,其中三个数字之和是5的倍数的三位数共有多少个?分析与解 要想求出三个数字之和是5的倍数的三位数共有多少个,不妨按从小分析与解到大的顺序把这些数写出来:104、109、113、118、122、127、……显然,用这种寻找答案的方法是可以的,但是太费时间了。
我们可以按下面的思路去思考。
这10个连续的三位数的三个数字之和,也正好是10个连续的自然数。
例如,A=1,B=2,那么上面写出的10个连续的三位数的三个数字之和为3、4、5、6、7、8、9、10、11、12。
其中有而且只有两个三位数的三个数字之和是5的倍数。
从100~999,这些三位数共900个,每10个连续三位数为一个“数段”,一共可以分成90个“数段”。
而每10个连续的三位数中有而且只有2个三位数的三个数字之和是5的倍数,所以在所有的三位数中共有 2×90=180个三位数,它们的三个数字和是5的倍数。
答:三位数中三个数字之和是5的倍数的共有180个。
例86 有一串数 1、4、9、16、25、26、49、……它们是按一定的规律排列的。
一位教育家说过:“教会学生思考,这对学生来说,是一生中最有价值的本钱。
”学习数学的本身,就是要在学懂数学知识的同时,学会思考,掌握思考的方法,培养和发展思维能力,提高思维水平。
我们几位从事小学数学教学工作的老师,就是以教会学生思考为出发点,结合学生学习的知识内容,编写《趣题巧算——百题百讲百练》这套书的。
全书分为一、二年级分册,三年级分册,四年级分册,五年级分册,六年级分册和综合分册。
书中列举百例,讲解这百题,同时又设计了一百道练习题供学生练习用。
通过小学生的自学,使他们学会思考。
另外,这本书也是教师开展课外数学小组活动及家长指导孩子学习数学的资料。
在编写这本小册子的过程中,我们选用了一些竞赛试题或一些他人设计的趣题,在此向这些作者致谢!编者水平有限,经验不足,书中如有不当之处,敬请读者提出批评指正。
编者1994年 10月李树德 1941年生。
原任北京市东城区地坛小学副校长,北京市和东城区数学奥林匹克学校骨干教师,特级教师,中学高级教师,中国数学奥林匹克一级教练员,第四届“华罗庚金杯”少年数学邀请赛主试委员会委员,第八届“北京市迎春杯数学竞赛”命题组成员。
长期从事小学数学教学工作,有扎实的专业知识和理论基础,他撰写的论文多次获优秀成果奖,多次在省市级刊物上发表有关数学教学文章。
热心于小学数学奥林匹克教学工作,是东城区数学奥林匹克学校创始人之一。
他培养的学生多次在区、市、全国数学竞赛中获奖。
为历届“迎春杯”赛主教练,为东城区在北京市迎春杯数学竞赛中夺得三连冠做出了贡献。
近年来参加编写了《“华罗庚金杯”少年数学邀请赛试题分析》、《小学数学标准化题型研究与练习》、《小学数学百问》、《数学奥林匹克电视讲座》等十余本书。
张玉山 1940年生。
北京市东城区和平里第二小学副校长,中学高级教师,中国奥林匹克一级教练员。
多年从事小学数学教学工作,有扎实的专业知识和理论基础。
撰写多篇论文,多次获优秀成果奖,多次应省市级刊物的邀请撰写有关数学的专栏文章及专题讲座。
小学数学趣题巧算百题百讲百练--杂题部分(1)小学生的课外数学活动,包括一些数学竞赛活动,极大地提高了小学生学习数学的兴趣和热情。
通过参加各种数学课外活动,提高了学生思维和探索能力。
杂题中选编的例题,更突出了小学数学知识的综合运用。
有的题涉及一点小学尚未学习的知识,但是学生还是可以理解的,题中介绍的各种解法,小学生应该掌握。
例84 将奇数1、3、5、7、9、……按下表排成五列。
例如,13排在第2行第2列,25排在第4行第4列。
那么1993排在第几行第几列?分析与解首先要算出1993这个数是这列数中的第几个数。
由上表可看出,每行有4个数,而997÷4=249……1。
就是说第997个数是第250行中最小的一个。
偶数行的数是从小到大依次排在第4、3、2、1列的,因此1993这个数排在第250行第 4列。
例85在自然数中有很多三位数,其中三个数字之和是5的倍数的三位数共有多少个?分析与解要想求出三个数字之和是5的倍数的三位数共有多少个,不妨按从小到大的顺序把这些数写出来:104、109、113、118、122、127、……显然,用这种寻找答案的方法是可以的,但是太费时间了。
我们可以按下面的思路去思考。
这10个连续的三位数的三个数字之和,也正好是10个连续的自然数。
例如,A=1,B=2,那么上面写出的10个连续的三位数的三个数字之和为3、4、5、6、7、8、9、10、11、12。
其中有而且只有两个三位数的三个数字之和是5的倍数。
从100~999,这些三位数共900个,每10个连续三位数为一个“数段”,一共可以分成90个“数段”。
而每10个连续的三位数中有而且只有2个三位数的三个数字之和是5的倍数,所以在所有的三位数中共有 2×90=180个三位数,它们的三个数字和是5的倍数。
答:三位数中三个数字之和是5的倍数的共有180个。
例86 有一串数 1、4、9、16、25、26、49、……它们是按一定的规律排列的。