小学数学趣题巧算 三年级分册含大量练习题、解析过程及答案
- 格式:pdf
- 大小:229.55 KB
- 文档页数:85

【导语】在⽇常⽣活中,常有⼀些妙趣横⽣、带有智⼒测试性质的问题,如:3个⼩朋友同时唱⼀⾸歌要3分钟,100个⼩朋友同时唱这⾸歌要⼏分钟?类似这样的问题⼀般不需要较复杂的计算,也不能⽤常规⽅法来解决,⽽常常需要⽤⼩朋友的灵感、技巧和机智获得答案。
以下是⽆忧考整理的《⼩学三年级奥数数学趣题》,希望帮助到您。
【篇⼀】 【例题】舒舒和思思到书店去买书,两⼈都想买《动脑筋》这本书,但钱都不够。
舒舒缺2元8⾓,思思缺1分钱,⽤两个⼈合起来的⼉买⼀本,仍然不够。
这本书多少钱? 【思路导航】思思买这本书缺1分钱,两个⼈合起来的钱买⼀本书仍然不够,这说明舒舒根本没有钱,所以这本书的价钱是2元8⾓。
练习题: 1、⼩华和娟娟到商店买⽂具盒,两⼈看中同⼀个⽂具盒,但钱都不够。
⼩华缺9元4⾓,娟娟缺1分,两⼈合起来买⼀个仍然不够。
这个⽂具盒多少钱? 2、李华和张洁到商店买同⼀种练本,但发现钱都没带够,李华缺6⾓,张洁缺2分钱,但两⼈合起来买⼀本仍不够。
这种本⼦⼀本多少钱? 3、王阿姨和李阿姨到商场买电视机,两⼈都看中同⼀种电视机,但王阿姨缺600元,李阿姨缺900元,⽤两⼈带的钱合起来买这⼀台电视机正好。
这台电视机多少钱?【篇⼆】 【例题】如果每⼈步⾏的速度相同,2个⼈⼀起从学校到⼉童乐园要3⼩时,那么6个⼈⼀起从学校到⼉童乐园要多少⼩时? 【思路导航】2个⼈⼀起从学校到⼉童乐园要3⼩时,也就是1个⼈从学校到⼉童乐园要3⼩时;6个⼈⼀起从学校到⼉童乐园所⽤的时间与⼀个⼈所⽤的时间相等,所以6个⼈⼀起从学校到⼉童乐园还是⽤3⼩时。
练习题: 1、3个⼈同时唱3⾸歌⽤9分钟,9个⼈同时唱同样的3⾸歌⽤⼏分钟? 2、5只猫5天能捉5只⽼⿏,照这样计算,要在100天⾥捉100只⽼⿏要多少只猫? 3、6个⼈从甲地到⼄地⽤4⼩时,如果每⼈的步⾏速度相同,那么3个⼈从甲地到⼄地要⽤⼏⼩时?【篇三】 【例题】⼩猫要把15条鱼分成数量不相等的4堆,问最多的⼀堆中最多可放⼏条鱼? 【思路导航】⼩猫要把15条鱼分成数量各不相等的4堆,要让最多的⼀堆中⼩鱼条数尽量多,那么其余三堆⼩鱼的条数就要尽量少。

三年级奥数讲座智巧趣题1、用数字1 , 1, 2, 2, 3, 3拼凑出一个六位数,使两个1之间有1个数字,两个2之间有2 个数字,两个3之间有3个数字。
解答:312132 2312132、把一根线绳对折,对折,再对折,然后从对折后的中间处剪开,这根线绳被剪成了多少段?解答:对折一次:2*2-仁3 段对折二次:4*2-3=5段对折三次:8*2-7=9段.3、有10张,卡片分别标有从2开始的10个连续偶数。
如果将它们分成5组,每组两张,计算同组中两个偶数和分别得到①34,②22,③16,④30,⑤&那么每组中的两张卡片上标的数各是多少?解答:10 个连续偶数是24,6,8,10,12,14,16,18,208=2+6 16=4+12 22=14+8 30=20+10 34=16+184、售货员把29个乒乓球分装在5个盒子里,使得只要顾客所买的乒乓个数小于30,他总可以恰好把其中的一盒或几盒卖出,而不必拆盒。
问这5个盒子里分别装着多少个乒乓球?解答:1+2+4+8+14=295、小明的左衣袋和右衣袋中分别装有6枚和8枚硬币,并且两衣袋中硬币的总钱数相等。
当任意从左边衣袋取出两个硬币与右边衣袋的任意两个硬币交换时,左边衣袋的钱总数要么比原来的钱数多2分,要么比原来的钱数少2分,那么两个衣袋中共有多少分钱?解答:2*6=5+7*1 共:2*6*2=24 分=2 角 4 分.6、如图10-1,这是用24根火柴摆成的两个正方形,请你只移动其中的4根火柴,使它变成两个完全相同的正方形。
■ • • • ■1、请将W 亍棋子分放在边长曲厘米、20煙米、W 匣米的3个盒子里,使大盒子里的棋子数 是中盒子毘棋子数的2倍,中盒子毘的棋子数是小盒子里棋子数的2倍。
河应当如何放置?解答*把小盒子放进中盒子里,大盒子另外放+小盒里放4亍,中盒里放4个,大盒里放W 个+ 歆今有101校硬币,其中有100枚同样的貞帀和I 枚伪币,伪币与真币和車量不同"现需弄清 楚伪帀究竟比真币轻,还是比真币重,但只有一架没有祛码的天平口那么怎样利用这架天平称两次, 来达到冃的?解答:分成50、50. t 三堆:第一次称两个5山如果平了,第二次从这40个任意拿1个〔当 然是真的)与第三堆的I 个称,自然会出结果:第一次称两个50不平是正常的,第二次我们把其中 的一堆(或重的或轻的都行)分成2乩25.称第二次:X 把轻的分成厉、25,如果平了.说明那 堆重的有假,当然假的是超重;如果不平,说明这50个轻的有假’假的是轻了; 2.把重的分成為、 25,道理同上。
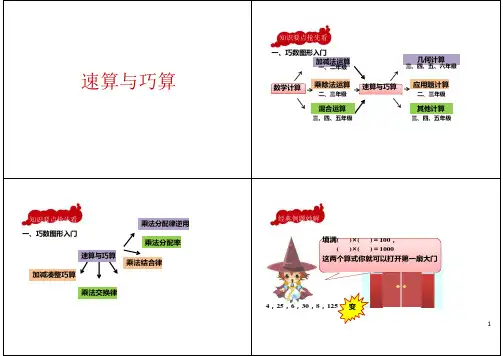
知识要点抢先看一、巧数图形入门加减法运算一、二年级几何计算三、四、五、六年级速算与巧算数学计算乘除法运算二、三年级混合运算三、四、五年级速算与巧算应用题计算二、三年级其他计算三、四、五年级知识要点抢先看一、巧数图形入门速算与巧算加减凑整巧算乘法分配律逆用乘法分配率乘法结合律经典例题妙解填满( )×( )=100,( )×( )=1000这两个算式你就可以打开第一扇大门乘法交换律4,25,6,30,8,125 变1党经典例题妙解 乘法交换律: 经典例题妙解 乘法结合律: 【例1】计算:⑴17 ⨯ 4 ⨯ 25,⑵125 ⨯ 19 ⨯ 8, ⑶8 ⨯ 375 ⨯ 125【例2】计算:⑴25 ⨯ 13 ⨯ 125 ⨯ 4 ⨯ 8,⑵25 ⨯ 9 ⨯ 8 ⨯ 8 ⨯ 125,常用乘除法基本运算公式(用字母表示) 乘法交换律:a ⨯ b = b ⨯ a乘法结合律:a ⨯ b ⨯ c = (a ⨯ b ) ⨯ c = a ⨯ (b ⨯ c ) 25×4=100 125×8=1000爱共 爱产 爱2乘法分配律:(a +b) ⨯c =a ⨯c +b ⨯c;(a -b) ⨯c =a ⨯c -b ⨯c经典例题妙解【例3】199772 ⨯ 199911 - 199771⨯ 199912 =经典例题妙解11×12=11×23=11×45=经典例题妙解【例4】29×11=,309×11=,149×11=,3672×11=,拉面大法变113变经典例题妙解重码数 101经典例题妙解【例5】12×101= ,123×1001 , 1234×10001 , 765×( )=765765经典例题妙解 经典例题妙解【拓展】12×10101123×1001001001【例6】今年是2012年,也是传说中的世界末日年,解开下面的算式,就能解除世界末日的魔咒啦! 快 来 拯 救 人 类 吧 ! 20122012×2013-20132013×20124经典例题妙解经典例题妙解【拓展】22×202=22×303=22×203=你们知道一根面条和个大饼拼成数字9退1补9法经典例题妙解【例7】23×99=123×999=123×9999=234×9999=5测试题1.计算:17⨯39 +17⨯ 25 +17⨯362.填空:777 + 777 - 777 ⨯777 ÷777 =3.填空:98⨯196 + 2 ⨯196 +198 =4.⑴125⨯(80 -4)⑵125⨯(80 +8)⑶(200 - 4) ⨯ 25 5.⑴54 + 99 ⨯99 + 45 ⑵9999⨯2222 + 3333⨯33346.计算⑴ 25⨯ (20 -4)⑵125⨯(40 +8)⑶(2000 + 8) ⨯125答案1.答案:17⨯39 +17⨯ 25 +17⨯36 =17⨯ (39 + 25 + 36) =17002.答案: 777 + 777 - 777 ⨯ 777 ÷ 777 = 777 + 777 - 777 ⨯(777 ÷ 777)= 777 + 777 - 777 = 777 +(777 - 777)= 777 3.答案: 98⨯196 + 2 ⨯196 +198 =196 ⨯(98 + 2)+198 =19600 +198 =197984.答案:⑴125⨯ (80 - 4) =125⨯80 -125⨯ 4 =10000 - 500 = 9500 ;⑵125⨯ (80 + 8) =125⨯80 +125⨯8 =10000 +1000 =11000 ;⑶(200 - 4) ⨯ 25 = 200⨯ 25 - 4⨯ 25 = 5000 -100 = 4900 。

第15讲趣题巧解为了考考同学们的智力和灵气,先提几个问题:一张长方形的纸,用剪刀剪掉一个角,还剩几个角把一根毛线对折两次后剪一刀,毛线被剪成了几段一树枝上有10只鸟,用汽枪打中了一只,树枝上还剩几只鸟这类智力问题很有趣,但回答时要小心,稍有不慎,就可能落入“圈套”;要想正确地解答这类题目,一是要全面考虑各种情况,二是要充分运用学过的数学知识,再就是还需要些思考问题的灵气和非常规的思考方法;例1一张长方形纸片有四个角,用剪刀沿直线剪掉一个角后,还剩几个角分析:由于已知“剪掉一个角”,但没有限制如何剪,所以必须对这个已知条件中的“剪法”有一个全面的考虑;否则,不加思索地顺口答出“还剩3个角”,答案就不全面了;当我们仔细考虑“剪法”的各种可能性后,再根据角的定义,就会得到全面而正确的答案;解:由于剪掉长方形纸片的一个角有下页图所示的三种不同剪法图中阴影部分为剪掉的角,所以,可能还有5个角、4个角或3个角;答:还剩5个角、4个角或3个角;例2 37个同学要坐船过河,渡口处只有一只能载5人的小船无船工;他们要全部渡过河去,至少要使用这只小船渡河多少次分析:如果由37÷5=7……2,得出7+1=8次,那么就错了;因为忽视了至少要有1个人将小船划回来这个特定的要求;实际情况是:小船前面的每一个来回至多只能渡4个人过河去,只有最后一次小船不用返回才能渡5个人过河;解:因为除最后一次可以渡5个人外,前面若干个来回每个来回只能渡过4个人,每个来回是2次渡河,所以至少渡河37-5÷4×2+1=17次;答:至少要渡河17次;例31右图是10枚硬币,移动其中1枚硬币,使每一行上都有6枚硬币;2用12根火柴拼出6个边长为1根火柴的正方形;分析与解:110枚硬币摆两行,一般来说每行有10÷2=5枚;图中的两行却是一行5枚一行6枚,原因是中间有1枚在两行的交叉点上,所以出现了5+6>10;由于题中并没有规定每个位置上只准放一枚,所以,只要使其中1枚硬币在两直行的交叉点上再“重复”一下,即在两行的交叉点上重叠地放2枚硬币见右上图,就可达到目的;2一个正方形需要4根火柴才能拼出,12根火柴只能拼出3个正方形,即使如左下图所示,也只能拼出4个正方形;如果我们放弃“在平面上拼”这种平常的思路,而改为在“立体空间中去拼”的新思路,那么就可能“柳暗花明”;当思路转向立体空间后,自然会联想到正方体图形;因为它有六个正方形表面,而且正方体的棱恰好是12条,所以完全符合题意;拼法如右上图所示;例3的解法说明,“换一个角度”或“换一个方向”去思考问题,往往能收到“奇效”本题2如果把思路始终局限在平面上那么就绝无出路;事实上,题目中并没有这样的限制,而是习惯的思维方式把我们限制了;一旦转到立体空间去思考,问题就迎刃而解了;例4一群动物在一起玩叠罗汉游戏;每只动物的重量都是整千克数,其中,最轻的重1千克,最重的重60千克;叠罗汉规定每只动物上面的总重量不能超过自己的重量;在重1~60千克的动物都有的情况下,它们最多能叠几层叠一个动物算一层分析与解:由于要求叠的层数尽量多,所以应该想到:①最上一层应是最轻的动物;②每只动物上面的总重量尽量等于自己的重量也满足“不超过”自己的重量要求;按这两条原则叠罗汉,能很容易找出各层的动物重量,从上到下,它们依次为:第1层第2层第3层第4层第5层第6层第7层第8层1 2 3612 24 4896因为96>60,所以这群动物最多只能叠七层罗汉;叠法不唯一如果只有重1,3,5,7,9,11,21千克的七个动物,按例4中的要求叠罗汉,那么最多能叠几层它是由哪些重量的动物叠出来的答案:5层;由重1, 3, 5, 9, 21千克的动物叠出例51小丽家里的闹钟每天早晨6点半准时响铃,提醒小丽起床,准备上学;有一次,小丽第二天要6点钟起床到学校去大扫除,她在头天晚上9点时把闹钟钟面时间调到8点半还是调到9点半,才能使闹钟第二天早晨6点钟响铃2小明和小强约定10点钟在学校门口碰面,小明的表慢5分钟,而他却以为慢10分钟;小强的表慢10分钟,而他却以为快5分钟;他俩会面时,谁迟到了先到者等了多少时间才见到迟到者分析与解:解决这两个问题的关键是弄清“正确时间”和“钟面时间”的含意;1要使闹铃6点钟响,即比平常提前半小时响,此时的钟面时间是6点半,它比正确时间多半小时;所以,在头天晚上9点调时针时,必须使钟面时间比正确时间多半小时,即应调到9点半;2以正确时间为准;小明以为他的表慢10分,所以,他比钟面时间提早10分到达,实际上他的钟面时间只比正确时间慢5分,所以小明提前了10-5=5分;小强以为他的表快5分,所以,他比钟面时间晚到5分,实际上他的钟面时间比正确时间慢10分,小强迟到了10+5=15分;会面时,小强迟到了,小明等了小强5+15=20分;例61三个小朋友三分钟削三支铅笔,照此效率,六个小朋友几分钟削六支铅笔2三只猫三天吃三只老鼠,照此效率,六只猫六天吃几只老鼠分析与解:这两个问题用来训练对倍数关系的准确理解;1中小朋友个数变成2倍,削的铅笔也变成2倍,所以,完成的时间应不变,即3分钟;如果具体分析,那么由已知条件推知,一个小朋友削一支铅笔需3分钟,所以,六个小朋友削六支铅笔还是需3分钟;2中猫的只数变成2倍,天数也变成2倍,所以,吃的老鼠只数就变成了2×2=4倍,即吃了3×4=12只;具体分析,由已知条件推知,一只猫三天吃一只老鼠,所以,当猫变成6倍六只,而天数不变时,就有六只猫三天吃1×6=6只老鼠;进而,当猫不变六只,而天数变为2倍六天时,就有六只猫六天吃老鼠6×2=12只;151.画三条线段,能构成几个角2.用6根长短、粗细一样的火柴棍拼出四个等边三角形即三边相等的三角形,如何拼3.一只挂钟,1点整敲1下,2点整敲2下……12点整敲12下,每半点整敲1下;一昼夜24时一共要敲多少下4.打靶时,小林和小峰各打了三枪,环数为1,2,4,5,7,9环;已知小林的总环数比小峰的总环数多6环;哪几环是小峰打的5.五个小朋友围坐在一个大圆桌边,按顺时针方向依次编为1,2,3,4,5号;老师给1,2,3,4,5号小朋友分别发1,2,3,4,5个苹果;从5号小朋友开始,依次按顺时针方向看,若邻坐的苹果比自己少,则送给对方一个;若邻坐的苹果不比自己少就不送;照此做下去,到第三圈为止,他们每人手中各有多少个苹果6.球场休息时,保管员慌忙中把甲、乙、丙三个运动员先前交给他的水瓶都递送错了,结果甲喝的是丙的;乙、丙各喝的是谁的7.有一个台称,只能称40千克以上的重量,甲、乙、丙三个小朋友的体重都在20~39千克之间,他们都想知道自己的体重;用这台称怎样才能知道他们各自的体重8.1三个小朋友三分钟削三支铅笔,九个小朋友六分钟削几支铅笔2三只猫三天吃三只老鼠,六只猫几天吃18只老鼠。


第二讲 速算与巧算(一)本讲主要介绍两种速算与巧算的方法: 1、理解并掌握分组凑整法; 2、理解并掌握加补凑整法.本章内容只涉及加减法中的速算与巧算,帮助学生在加减法运算中掌握基本的运算技巧,更加快速,更加准确地解决加减法运算中的 “难题”.计算: (1)6+6+6+6+6+4 (2)6+7+8+9+10+11+12+13+14分析:原式=5×6+4 分析:原式=(6+14)+(7+13)+(8+12)+(9+11)+10 =34 =90(3)1+2+3+4+5+4+3+2 (4)7+17+27+37=88分析:原式=24 分析:原式=(10-3)+(20-3)+(30-3)+(40-3) =88(5)58-26-28 (6)64-(25+14)分析:原式=58-28-26 分析:原式=64-14-25 =4 =25教学目标想挑 战吗 ?一位济贫劫富的大侠夜间潜入一吝啬的财主家,盗得一宝箱,非常高兴离去,但是当他要打开宝箱时却发愁了,宝箱是一个密码箱,要在6 4 8 9 7四个数之间填入“+”和“-”,使他们的结果等于4,这样宝箱才会自动打开。
哪位同学可以帮助这位大侠? 答案:6+4-8+9-7=4. 你还记得吗?专题精讲在这一讲中我们我们将会学习有关加减法的速算与巧算的方法.我们在进行加减法运算时,为了又快又准确,除了熟练地掌握计算法则以外,还需要掌握一些巧算方法.加减法的巧算主要是“凑整”,就是将算式中的数分成若干组,使每组的运算结果都是整十、整百、整千......的数,再将各组的结果求和(差),这样使我们在加减法运算中更加迅速,更加准确.在具体的凑数运算过程中,我们主要涉及到几种计算方法:(1)分组凑整法,(2)加补凑整法,(3)其他类型的巧算.我们在进行加法的巧算时,经常运用以下两个运算律:(1)加法交换律:两个数相加,交换加数的位置,他们的和不变.即a+b=b+a其中a,b各表示任意一数.例如,7+8=8+7=15.将此运算律推广,多个数相加,任意交换相加的次序,其和不变.(2)加法结合律:三个数相加,先把前两个数相加,再加上第三个数;或者先把后两个数相加,再与第一个数相加,他们的和不变.即a+b+c=(a+b)+c=a+(b+c)其中a,b,c各表示任意一数.例如,5+6+8=(5+6)+8=5+(6+8).将此运算律推广,多个数相加,也可以把其中的任意两个数或者多个数相加,其和不变.我们在进行减法运算时,经常运用以下性质:(3)在连减或者加减混合运算中,如果算式中没有括号,那么计算时要带数字前面的运算符号“搬家”.例如:a-b-c=a-c-b,a-b+c=a+c-b,其中a,b,c各表示一个数.(4)在加减法混合运算中,去括号时:如果括号前面是“+”号,那么去掉括号后,括号内的数的运算符号不变;如果括号前面是“-”号,那么去掉括号后,括号内的数的运算符号“+”变为“-”,“-”变为“+”.如:a+(b-c)=a+b-ca-(b+c)=a-b-ca-(b-c)=a-b+c(5)在加、减法混合运算中,添括号时:如果添加的括号前面是“+”,那么括号内的数的原运算符号不变;如果添加的括号前面是“-”,那么括号内的数的原运算符号“+”变为“-”,“-”变为“+”.如:a+b-c=a+(b-c)a-b+c=a-(b-c),a-b-c=a-(b+c)(一)分组凑整法【例1】(★★★奥数网题库)计算:(1)117+229+333+471+528+622(2)168+253+532(3)(1350+249+468)+(251+332+1650)(4)358+127+142+73分析:在这个例题中,主要让学生掌握加法分组凑整的方法.具体分析如下:(1)原式=(117+333)+(229+471)+(528+622)=450+700+1150=(450+1150)+700=1600+700=2300(2)原式=(168+532)+253=700+253=953(3)原式=1350+249+468+251+332+1650=(1350+1650)+(249+251)+(468+332)=3000+500+800=4300(4)原式=(358+142)+(127+73)=500+200=700【例2】(★★★奥数网题库)计算:(1)265-68-132(2)756-248-352(3)268-56-82-44-18(4)894-89-111-95-105-94分析:在这个例题中,主要让学生掌握减法分组凑整的方法.一个数连续减去两个数,可以先把后两个数相加凑整,再用这个数减去后两个数的和.具体分析如下:(1)原式=265-(68+132)=265-200=65(2)原式=756-(248+352)=756-600=156(3)原式=268-(56+44)-(82+18)=268-100-100=68(4)原式=(894-94)-(89+111)-(95+105)=800-200-200=400【例3】(★★★奥数网题库)计算:(1)98-53+102+63(2)163-154+245+137+55-146(3)1348-234-76+2234-48-24(4)1847-1936+536-154-46分析:在这个例题中,主要让学生掌握加减法混合运算分组凑整的方法,在凑整的过程中,要注意运算符号的变化或者带着符号搬家.具体分析如下:(1)原式=(98+102)+(63-53)=200+10=210(2)原式=(163+137)-(154+146)+(245+55)=300-300+300=300(3)原式=(1348-48)+(2234-234)-(76+24)=1300+2000-100=3200(4)原式=1847-(1936-536)-(154+46)=1847-1400-200=247[巩固] :(1)968-561-168-139,(2)456-(256+165),(3)582+(436-482),(4)264+451-216+136-184+149分析:(1)原式=(968-168)-(561+139)=800-700=100(2)原式=456-256-165=200-165=35(3)原式=582-482+436=100+436=536(4)原式=(264+136)+(451+149)-(216+184)=400+600-400=600[拓展1](我爱数学少年数学夏令营)计算:1997+1-2-3+4+5-6-7+8+9-10-11+……+1993-1994-1995+1996 分析:原式=1997+(1-2-3+4)+(5-6-7+8)+……+(1993-1994-1995+1996)=1997+0+0+……+0=1997[拓展2](2005全国小学数学奥林匹克)计算:2005+2004-2003-2002+2001+2000-1999-1998+1997+1996-……-7-6+5+4-3-2+1分析:将后四项每四项分为一组,每组的计算结果都是0,后2004项的计算结果都是0,剩下第一项,结果是2005.[拓展3](北大数学邀请赛)计算:1989+1988+1987-1986-1985-1984+1983+1982+1981-1980-1979-1978+……+9+8+7-6-5-4+3+2+1分析:从1989开始,每6个数一组,1989+1988+1987-1986-1985-1984=9,以后每一组6个数加、减后都等于9.1989÷6=331……3.最后剩下三个数3,2,1,3+2+1=6.因此,原式=331×9+6=2985.[拓展4] 计算 6472-(4476-2480)+5319-(3323-1327)+9354-(7358-5362)+6839-(4843-2847)分析:原式=(6472+5318+1)+(9354+6836+3)-(4480-2480-4)-(3327-1327-4)-(7362-5362-4)-(4847-2847-4)=11790+16190-2000-2000-2000-2000+20=27980-8000+20=20000(二)加补凑整法【例4】(★★★奥数网题库)计算:(1)165+199(2)198+96+297+10(3)298+396+495+691+799+21(4)195+196+197+198+199+15分析:在这个例题中,主要让学生掌握加法运算加补凑整的方法.具体分析如下:(1)(法1)原式=165+200-1 (法2)原式=164+1+199=365-1 =164+200=364 =364(2)(法1)原式=(198+2)+(96+4)+(297+3)+1=200+100+300+1=601(法2)原式=(200-2)+(100-4)+(300-3)+10=200+100+300-2-4-3+10=601(3)(法1)原式=298+396+495+691+799+2+4+5+9+1=(298+2)+(396+4)+(495+5)+(691+9)+(799+1)=300+400+500+700+800=2700(法2)原式=(300-3)+(400-4)+(500-5)+(700-9)+(800-1)+21=300+400+500+700+800-3-4-5-9-1+21=2700(4)(法1)原式=(195+5)+(196+4)+(197+3)+(198+2)+(199+1)=200+200+200+200+200=1000(法2)原式=(200-5)+(200-4)+(200-3)+(200-2)+(200-1)+15=200+200+200+200+200=1000[前铺] 计算:(1)65+99 (2) 36+102 (3) 258-98 (4) 351-103分析:(1)原式=65+100-1=165-1=164;(2)原式=36+100+2=136+2=138;(3)原式=258-100+2=158+2=160;(4)原式=351-100-3=251-3=248;通过以上题目的运算,我们发现一个快捷运算的规律:在(1)中,在加100时多加了1,所以要减去,这样保证结果不变,所以“多加的要减去”;(2)中,少加了2,在后面要加上,所以“少加的要加上”;(3)中,多减了2,所以要加上,所以“多减的要加上”;(4)中,少减了3,后面要再减去3,所以“少减的要再减”.这几种基本的加补凑整计算的方法,老师要引导学生理解,并加深巩固.【例5】(★★★奥数网题库)计算:(1)895-504-97(2)98-96-97-105+102+101(3)399+403+297-501(4)196+198-102-97分析:在这个例题中,主要让学生掌握加减法混合运算中加补凑整的方法.具体分析如下:(1)原式=(900-5)-(500+4)-(100-3)=900-500-100-5-4+3=294(2)原式=(100-2)-(100-4)-(100-3)-(100+5)+(100+2)+(100+1)=100-100-100-100+100+100-2+4+3-5+2+1=3(3)原式=(400-1)+(400+3)+(300-3)-(500+1)=400-1+400+3+300-3-500-1=598(4)原式=(200-4)+(200-2)-(100+2)-(100-3)=200+200-100-100-4-2-2+3=195[巩固] :(1)697+811,(2)709-698,(3)198-205-308+509,(4)501+502+503-398-397-396.分析:(1)原式=(700-3)+(800+11)=700+800-3+11=1508(2)原式=(700+9)-(700-2)=11(3)原式=(200-2)-(200+5)-(300+8)+(500+9)=200-200-300+500-2-5-8+9=194(4)原式=(500+1)+(500+2)+(500+3)-(400-2)-(400-3)-(400-4)=315. [拓展1] 计算:195+196+197+198+199分析:原式=(200-5)+(200-4)+(200-3)+(200-2)+(200-1)=200×5-(5+4+3+2+1)=1000-15=985[拓展2] (07年7月仁华入学测试题)83+86+95-85+86-94+95+94+86+92+87+80+93+100-89+83+96+98分析:原式=83+86+95-83-2+86-94+95+94+86+92+87+80+93+100-87-2+83+96+98 =90×12-4+5-2-4+5-4+2-10+3+10-2-7+6+8=1080+6=1086[拓展3](2006香港圣公会小学数学奥林匹克)89+899+8999+89999+899999分析:原式=(90-1)+(900-1)+(9000-1)+(90000-1)+(900000-1)=90+900+9000+90000+900000-5=999990-5=999985[拓展4](华罗庚金杯少年数学邀请赛)计算 11+192+1993+19994+199995所得和数的数字之和是多少?分析:原式=(20-9)+(200-8)+(2000-7)+(20000-6)+(200000-5)=(20+200+2000+20000+200000)-(9+8+7+6+5)=222220-35=222185故所得数字之和等于2+2+2+1+8+5=20.(三)其他常见类型巧算【例6】(★★★仁华试题)计算100-101+102-103+104-105+106-107+108分析:原式=100+(102-101)+(104-103)+(106-105)+(108-107)=100+1+1+1+1=104【例7】(★★★仁华试题)计算:123+234+345-456+567-678+789分析:方法1:原式=123+234+345+(567-456)+(789-678)=123+234+345+111+111=234+(123+567)=234+690=924方法2:原式=123+(123+111)+(123+222)-(123+333)+(123+444)-(123+555)+(123+666)=123×3+(111+222-333+444-555+666)=369+555=924【例8】(★★★仁华试题)计算1234+3142+4321+2413分析:原式=(1000+200+30+4)+(3000+100+40+2)+(4000+300+20+1)+(2000+400+10+3)=(1000+2000+3000+4000)+(100+200+300+400)+(10+20+30+40)+(1+2+3+4)=10000+1000+100+10=11110【例9】(★★★★仁华试题)计算19971997+9971997+971997+71997+1997+997+97+7分析:原式=(19972000-3)+(9972000-3)+(972000-3)+(72000-3)+(2000-3)+(1000-3)+(100-3)+(10-3)=19972000+9972000+972000+72000+2000+1000+100+10-8×3=30991110-24=30991086【例10】(★★★★★仁华试题)在右图的36个格子中各有一个数,最上面一横行和最左面一竖列中的数已经填好,其余每个格子中的数等于每个格子同一横行最左面数与同一竖列最上面数之和(例如:a=14+17=31),问这36个数的总和是多少?分析:第二横行的空格应该填的数字分别是11+12,13+12,15+12,17+12,19+12,同理,下面每一横行都是用竖列的一个数与横行的每一个数相加.我们最后要求这36个格子中的所有数字之和,第一横行的和为:10+11+13+15+17+19=(10+15)+(11+19)+(13+17)=85,第二横行的和为:12+11+12+13+12+15+12+17+12+19+12=12×6+(11+13+15+17+19)=147,同理,第三横行的和为:14+11+14+13+14+15+14+17+14+19+14=14×6+(11+13+15+17+19)=159,第四横行的和为16×6+75=171,第五横行的和为:18×6+75=183,第六横行的和为:20×6+75=195.所以36个格子的和为85+147+159+171+183+195=940.方法2:法1比较笨拙,没有体现该题解法的精髓,在我们解这道题之前,我们看看下面的例子:2 3 4 5468上表空格处的数等于每个格子同一横行最左面数与同一竖列最上面数之和,求这16个数之和。

第二讲 速算与巧算(一)本讲主要介绍两种速算与巧算的方法: 1、理解并掌握分组凑整法; 2、理解并掌握加补凑整法.本章内容只涉及加减法中的速算与巧算,帮助学生在加减法运算中掌握基本的运算技巧,更加快速,更加准确地解决加减法运算中的 “难题”.计算: (1)6+6+6+6+6+4 (2)6+7+8+9+10+11+12+13+14分析:原式=5×6+4 分析:原式=(6+14)+(7+13)+(8+12)+(9+11)+10 =34 =90(3)1+2+3+4+5+4+3+2 (4)7+17+27+37=88分析:原式=24 分析:原式=(10-3)+(20-3)+(30-3)+(40-3) =88(5)58-26-28 (6)64-(25+14)分析:原式=58-28-26 分析:原式=64-14-25 =4 =25教学目标想挑 战吗 ?一位济贫劫富的大侠夜间潜入一吝啬的财主家,盗得一宝箱,非常高兴离去,但是当他要打开宝箱时却发愁了,宝箱是一个密码箱,要在6 4 8 9 7四个数之间填入“+”和“-”,使他们的结果等于4,这样宝箱才会自动打开。
哪位同学可以帮助这位大侠? 答案:6+4-8+9-7=4. 你还记得吗?专题精讲在这一讲中我们我们将会学习有关加减法的速算与巧算的方法.我们在进行加减法运算时,为了又快又准确,除了熟练地掌握计算法则以外,还需要掌握一些巧算方法.加减法的巧算主要是“凑整”,就是将算式中的数分成若干组,使每组的运算结果都是整十、整百、整千......的数,再将各组的结果求和(差),这样使我们在加减法运算中更加迅速,更加准确.在具体的凑数运算过程中,我们主要涉及到几种计算方法:(1)分组凑整法,(2)加补凑整法,(3)其他类型的巧算.我们在进行加法的巧算时,经常运用以下两个运算律:(1)加法交换律:两个数相加,交换加数的位置,他们的和不变.即a+b=b+a其中a,b各表示任意一数.例如,7+8=8+7=15.将此运算律推广,多个数相加,任意交换相加的次序,其和不变.(2)加法结合律:三个数相加,先把前两个数相加,再加上第三个数;或者先把后两个数相加,再与第一个数相加,他们的和不变.即a+b+c=(a+b)+c=a+(b+c)其中a,b,c各表示任意一数.例如,5+6+8=(5+6)+8=5+(6+8).将此运算律推广,多个数相加,也可以把其中的任意两个数或者多个数相加,其和不变.我们在进行减法运算时,经常运用以下性质:(3)在连减或者加减混合运算中,如果算式中没有括号,那么计算时要带数字前面的运算符号“搬家”.例如:a-b-c=a-c-b,a-b+c=a+c-b,其中a,b,c各表示一个数.(4)在加减法混合运算中,去括号时:如果括号前面是“+”号,那么去掉括号后,括号内的数的运算符号不变;如果括号前面是“-”号,那么去掉括号后,括号内的数的运算符号“+”变为“-”,“-”变为“+”.如:a+(b-c)=a+b-ca-(b+c)=a-b-ca-(b-c)=a-b+c(5)在加、减法混合运算中,添括号时:如果添加的括号前面是“+”,那么括号内的数的原运算符号不变;如果添加的括号前面是“-”,那么括号内的数的原运算符号“+”变为“-”,“-”变为“+”.如:a+b-c=a+(b-c)a-b+c=a-(b-c),a-b-c=a-(b+c)(一)分组凑整法【例1】(★★★奥数网题库)计算:(1)117+229+333+471+528+622(2)168+253+532(3)(1350+249+468)+(251+332+1650)(4)358+127+142+73分析:在这个例题中,主要让学生掌握加法分组凑整的方法.具体分析如下:(1)原式=(117+333)+(229+471)+(528+622)=450+700+1150=(450+1150)+700=1600+700=2300(2)原式=(168+532)+253=700+253=953(3)原式=1350+249+468+251+332+1650=(1350+1650)+(249+251)+(468+332)=3000+500+800=4300(4)原式=(358+142)+(127+73)=500+200=700【例2】(★★★奥数网题库)计算:(1)265-68-132(2)756-248-352(3)268-56-82-44-18(4)894-89-111-95-105-94分析:在这个例题中,主要让学生掌握减法分组凑整的方法.一个数连续减去两个数,可以先把后两个数相加凑整,再用这个数减去后两个数的和.具体分析如下:(1)原式=265-(68+132)=265-200=65(2)原式=756-(248+352)=756-600=156(3)原式=268-(56+44)-(82+18)=268-100-100=68(4)原式=(894-94)-(89+111)-(95+105)=800-200-200=400【例3】(★★★奥数网题库)计算:(1)98-53+102+63(2)163-154+245+137+55-146(3)1348-234-76+2234-48-24(4)1847-1936+536-154-46分析:在这个例题中,主要让学生掌握加减法混合运算分组凑整的方法,在凑整的过程中,要注意运算符号的变化或者带着符号搬家.具体分析如下:(1)原式=(98+102)+(63-53)=200+10=210(2)原式=(163+137)-(154+146)+(245+55)=300-300+300=300(3)原式=(1348-48)+(2234-234)-(76+24)=1300+2000-100=3200(4)原式=1847-(1936-536)-(154+46)=1847-1400-200=247[巩固] :(1)968-561-168-139,(2)456-(256+165),(3)582+(436-482),(4)264+451-216+136-184+149分析:(1)原式=(968-168)-(561+139)=800-700=100(2)原式=456-256-165=200-165=35(3)原式=582-482+436=100+436=536(4)原式=(264+136)+(451+149)-(216+184)=400+600-400=600[拓展1](我爱数学少年数学夏令营)计算:1997+1-2-3+4+5-6-7+8+9-10-11+……+1993-1994-1995+1996 分析:原式=1997+(1-2-3+4)+(5-6-7+8)+……+(1993-1994-1995+1996)=1997+0+0+……+0=1997[拓展2](2005全国小学数学奥林匹克)计算:2005+2004-2003-2002+2001+2000-1999-1998+1997+1996-……-7-6+5+4-3-2+1分析:将后四项每四项分为一组,每组的计算结果都是0,后2004项的计算结果都是0,剩下第一项,结果是2005.[拓展3](北大数学邀请赛)计算:1989+1988+1987-1986-1985-1984+1983+1982+1981-1980-1979-1978+……+9+8+7-6-5-4+3+2+1分析:从1989开始,每6个数一组,1989+1988+1987-1986-1985-1984=9,以后每一组6个数加、减后都等于9.1989÷6=331……3.最后剩下三个数3,2,1,3+2+1=6.因此,原式=331×9+6=2985.[拓展4] 计算 6472-(4476-2480)+5319-(3323-1327)+9354-(7358-5362)+6839-(4843-2847)分析:原式=(6472+5318+1)+(9354+6836+3)-(4480-2480-4)-(3327-1327-4)-(7362-5362-4)-(4847-2847-4)=11790+16190-2000-2000-2000-2000+20=27980-8000+20=20000(二)加补凑整法【例4】(★★★奥数网题库)计算:(1)165+199(2)198+96+297+10(3)298+396+495+691+799+21(4)195+196+197+198+199+15分析:在这个例题中,主要让学生掌握加法运算加补凑整的方法.具体分析如下:(1)(法1)原式=165+200-1 (法2)原式=164+1+199=365-1 =164+200=364 =364(2)(法1)原式=(198+2)+(96+4)+(297+3)+1=200+100+300+1=601(法2)原式=(200-2)+(100-4)+(300-3)+10=200+100+300-2-4-3+10=601(3)(法1)原式=298+396+495+691+799+2+4+5+9+1=(298+2)+(396+4)+(495+5)+(691+9)+(799+1)=300+400+500+700+800=2700(法2)原式=(300-3)+(400-4)+(500-5)+(700-9)+(800-1)+21=300+400+500+700+800-3-4-5-9-1+21=2700(4)(法1)原式=(195+5)+(196+4)+(197+3)+(198+2)+(199+1)=200+200+200+200+200=1000(法2)原式=(200-5)+(200-4)+(200-3)+(200-2)+(200-1)+15=200+200+200+200+200=1000[前铺] 计算:(1)65+99 (2) 36+102 (3) 258-98 (4) 351-103分析:(1)原式=65+100-1=165-1=164;(2)原式=36+100+2=136+2=138;(3)原式=258-100+2=158+2=160;(4)原式=351-100-3=251-3=248;通过以上题目的运算,我们发现一个快捷运算的规律:在(1)中,在加100时多加了1,所以要减去,这样保证结果不变,所以“多加的要减去”;(2)中,少加了2,在后面要加上,所以“少加的要加上”;(3)中,多减了2,所以要加上,所以“多减的要加上”;(4)中,少减了3,后面要再减去3,所以“少减的要再减”.这几种基本的加补凑整计算的方法,老师要引导学生理解,并加深巩固.【例5】(★★★奥数网题库)计算:(1)895-504-97(2)98-96-97-105+102+101(3)399+403+297-501(4)196+198-102-97分析:在这个例题中,主要让学生掌握加减法混合运算中加补凑整的方法.具体分析如下:(1)原式=(900-5)-(500+4)-(100-3)=900-500-100-5-4+3=294(2)原式=(100-2)-(100-4)-(100-3)-(100+5)+(100+2)+(100+1)=100-100-100-100+100+100-2+4+3-5+2+1=3(3)原式=(400-1)+(400+3)+(300-3)-(500+1)=400-1+400+3+300-3-500-1=598(4)原式=(200-4)+(200-2)-(100+2)-(100-3)=200+200-100-100-4-2-2+3=195[巩固] :(1)697+811,(2)709-698,(3)198-205-308+509,(4)501+502+503-398-397-396.分析:(1)原式=(700-3)+(800+11)=700+800-3+11=1508(2)原式=(700+9)-(700-2)=11(3)原式=(200-2)-(200+5)-(300+8)+(500+9)=200-200-300+500-2-5-8+9=194(4)原式=(500+1)+(500+2)+(500+3)-(400-2)-(400-3)-(400-4)=315. [拓展1] 计算:195+196+197+198+199分析:原式=(200-5)+(200-4)+(200-3)+(200-2)+(200-1)=200×5-(5+4+3+2+1)=1000-15=985[拓展2] (07年7月仁华入学测试题)83+86+95-85+86-94+95+94+86+92+87+80+93+100-89+83+96+98分析:原式=83+86+95-83-2+86-94+95+94+86+92+87+80+93+100-87-2+83+96+98 =90×12-4+5-2-4+5-4+2-10+3+10-2-7+6+8=1080+6=1086[拓展3](2006香港圣公会小学数学奥林匹克)89+899+8999+89999+899999分析:原式=(90-1)+(900-1)+(9000-1)+(90000-1)+(900000-1)=90+900+9000+90000+900000-5=999990-5=999985[拓展4](华罗庚金杯少年数学邀请赛)计算 11+192+1993+19994+199995所得和数的数字之和是多少?分析:原式=(20-9)+(200-8)+(2000-7)+(20000-6)+(200000-5)=(20+200+2000+20000+200000)-(9+8+7+6+5)=222220-35=222185故所得数字之和等于2+2+2+1+8+5=20.(三)其他常见类型巧算【例6】(★★★仁华试题)计算100-101+102-103+104-105+106-107+108分析:原式=100+(102-101)+(104-103)+(106-105)+(108-107)=100+1+1+1+1=104【例7】(★★★仁华试题)计算:123+234+345-456+567-678+789分析:方法1:原式=123+234+345+(567-456)+(789-678)=123+234+345+111+111=234+(123+567)=234+690=924方法2:原式=123+(123+111)+(123+222)-(123+333)+(123+444)-(123+555)+(123+666)=123×3+(111+222-333+444-555+666)=369+555=924【例8】(★★★仁华试题)计算1234+3142+4321+2413分析:原式=(1000+200+30+4)+(3000+100+40+2)+(4000+300+20+1)+(2000+400+10+3)=(1000+2000+3000+4000)+(100+200+300+400)+(10+20+30+40)+(1+2+3+4)=10000+1000+100+10=11110【例9】(★★★★仁华试题)计算19971997+9971997+971997+71997+1997+997+97+7分析:原式=(19972000-3)+(9972000-3)+(972000-3)+(72000-3)+(2000-3)+(1000-3)+(100-3)+(10-3)=19972000+9972000+972000+72000+2000+1000+100+10-8×3=30991110-24=30991086【例10】(★★★★★仁华试题)在右图的36个格子中各有一个数,最上面一横行和最左面一竖列中的数已经填好,其余每个格子中的数等于每个格子同一横行最左面数与同一竖列最上面数之和(例如:a=14+17=31),问这36个数的总和是多少?分析:第二横行的空格应该填的数字分别是11+12,13+12,15+12,17+12,19+12,同理,下面每一横行都是用竖列的一个数与横行的每一个数相加.我们最后要求这36个格子中的所有数字之和,第一横行的和为:10+11+13+15+17+19=(10+15)+(11+19)+(13+17)=85,第二横行的和为:12+11+12+13+12+15+12+17+12+19+12=12×6+(11+13+15+17+19)=147,同理,第三横行的和为:14+11+14+13+14+15+14+17+14+19+14=14×6+(11+13+15+17+19)=159,第四横行的和为16×6+75=171,第五横行的和为:18×6+75=183,第六横行的和为:20×6+75=195.所以36个格子的和为85+147+159+171+183+195=940.方法2:法1比较笨拙,没有体现该题解法的精髓,在我们解这道题之前,我们看看下面的例子:2 3 4 5468上表空格处的数等于每个格子同一横行最左面数与同一竖列最上面数之和,求这16个数之和。
小学数学趣题巧算(一)1.钟声小明家离火车站很近,他每天都可以根据车站大楼的钟声起床。
车站大楼的钟,每敲响一下延时3秒,间隔1秒后再敲第二下。
假如从第一下钟声响起,小明就醒了,那么到小明确切判断出已是清晨6点,前后共经过了几秒钟?2.越减越多同学们对这样的问题可能并不陌生:“一个长方形被切去1个角,还剩几个角?”这种题的最大特点是答案不唯一,要根据去掉的这个角的不同情况来确定“剩角”的多少。
图1以上3幅示意图,表明了3种不同情况的3种不同答案。
其中第3种情况最有趣,长方形原有4个角,切去了1个角,反而多了1个角,出现了越减越多的情况。
下面一道题的思考方法与上题类似,看你能否正确回答。
“一个正方体,锯掉一个角,还剩几个角?”请注意,这里的“角”是立体的“角”,它不同于平面上的角。
3.数一数如果有人问你“会数数儿吗?”,你会不屑一顾地说:“这么大了,还不会数数儿!”其实,数数儿的学问还是很大的。
不信,请你数出下面几何图形的个数。
图24.画一画下面这些图形你能一笔画出来吗?(不重复画)图35.最短的路线养貂专业户养殖场内安置了9个貂笼(如下图)。
为了节省每次喂食的时间,他必须走一条最短的路,但又不能漏掉一个貂笼,喂完食后还要回到原出发点。
你能替他设计一条最短的路线吗?并算出每喂食一次,至少要走多少米的路。
6.切西瓜六(1)班召开夏夜乘凉晚会,买来了许多西瓜。
班主任李老师说:“今天买来了许多西瓜请大家吃。
在吃以前我先要以切西瓜为名请大家做一道数学题。
我规定,西瓜只能竖切,不能横剖。
大家知道,切一刀最多分成2块,切2刀最分成多4块,那么切3刀最多能分成几块?切4刀、切5刀、切6刀呢?这中间有没有规律?如果有规律,请同学们找出来。
”李老师刚说完,同学们就七嘴八舌地讨论起来。
请你也参加他们的讨论吧。
7.均分承包田有一块等腰梯形菜地(如下图),地边有一口水井。
现在3户种菜专业户都提出要承包这块地。
经研究,决定让这3户共同承包这块地,因此必须把这块地分成面积相等、形状相同且与这口水井的距离也要相等的3块地。

三年级奥数讲座智巧趣题1、用数字1,1,2,2,3,3拼凑出一个六位数,使两个1之间有1个数字,两个2之间有2个数字,两个3之间有3个数字。
解答:312132 2312132、把一根线绳对折,对折,再对折,然后从对折后的中间处剪开,这根线绳被剪成了多少段?解答:对折一次: 2*2-1=3段对折二次:4*2-3=5段对折三次:8*2-7=9段.3、有10张,卡片分别标有从2开始的10个连续偶数。
如果将它们分成5组,每组两张,计算同组中两个偶数和分别得到①34,②22,③16,④30,⑤8。
那么每组中的两张卡片上标的数各是多少?解答:10个连续偶数是:2,4,6,8,10,12,14,16,18,208=2+6 16=4+12 22=14+8 30=20+10 34=16+184、售货员把29个乒乓球分装在5个盒子里,使得只要顾客所买的乒乓个数小于30,他总可以恰好把其中的一盒或几盒卖出,而不必拆盒。
问这5个盒子里分别装着多少个乒乓球?解答:1+2+4+8+14=295、小明的左衣袋和右衣袋中分别装有6枚和8枚硬币,并且两衣袋中硬币的总钱数相等。
当任意从左边衣袋取出两个硬币与右边衣袋的任意两个硬币交换时,左边衣袋的钱总数要么比原来的钱数多2分,要么比原来的钱数少2分,那么两个衣袋中共有多少分钱?解答:2*6=5+7*1 共:2*6*2=24分=2角4分.6、如图10-1,这是用24根火柴摆成的两个正方形,请你只移动其中的4根火柴,使它变成两个完全相同的正方形。
解答:7、请将16个棋子分放在边长30厘米、20厘米、10厘米的3个盒子里,使大盒子里的棋子数是中盒子里棋子数的2倍,中盒子里的棋子数是小盒子里棋子数的2倍。
问应当如何放置?解答:把小盒子放进中盒子里,大盒子另外放.小盒里放4个,中盒里放4个,大盒里放8个.8、今有101枚硬币,其中有100枚同样的真币和1枚伪币,伪币与真币和重量不同。
现需弄清楚伪币究竟比真币轻,还是比真币重,但只有一架没有砝码的天平。

一位教育家说过:“教会学生思考,这对学生来说,是一生中最有价值的本钱。
”学习数学的本身,就是要在学懂数学知识的同时,学会思考,掌握思考的方法,培养和发展思维能力,提高思维水平。
我们几位从事小学数学教学工作的老师,就是以教会学生思考为出发点,结合学生学习的知识内容,编写《趣题巧算——百题百讲百练》这套书的。
全书分为一、二年级分册,三年级分册,四年级分册,五年级分册,六年级分册和综合分册。
书中列举百例,讲解这百题,同时又设计了一百道练习题供学生练习用。
通过小学生的自学,使他们学会思考。
另外,这本书也是教师开展课外数学小组活动及家长指导孩子学习数学的资料。
在编写这本小册子的过程中,我们选用了一些竞赛试题或一些他人设计的趣题,在此向这些作者致谢!编者水平有限,经验不足,书中如有不当之处,敬请读者提出批评指正。
编者1994年 10月李树德 1941年生。
原任北京市东城区地坛小学副校长,北京市和东城区数学奥林匹克学校骨干教师,特级教师,中学高级教师,中国数学奥林匹克一级教练员,第四届“华罗庚金杯”少年数学邀请赛主试委员会委员,第八届“北京市迎春杯数学竞赛”命题组成员。
长期从事小学数学教学工作,有扎实的专业知识和理论基础,他撰写的论文多次获优秀成果奖,多次在省市级刊物上发表有关数学教学文章。
热心于小学数学奥林匹克教学工作,是东城区数学奥林匹克学校创始人之一。
他培养的学生多次在区、市、全国数学竞赛中获奖。
为历届“迎春杯”赛主教练,为东城区在北京市迎春杯数学竞赛中夺得三连冠做出了贡献。
近年来参加编写了《“华罗庚金杯”少年数学邀请赛试题分析》、《小学数学标准化题型研究与练习》、《小学数学百问》、《数学奥林匹克电视讲座》等十余本书。
张玉山 1940年生。
北京市东城区和平里第二小学副校长,中学高级教师,中国奥林匹克一级教练员。
多年从事小学数学教学工作,有扎实的专业知识和理论基础。
撰写多篇论文,多次获优秀成果奖,多次应省市级刊物的邀请撰写有关数学的专栏文章及专题讲座。
