公法线计算 公式

公法线长度及其极限偏差
一、什么是公法线
公法线，也称为公坐标系统（GCC），是一种特殊的度量标准，用来衡量地球表面两
个点间的距离和方位。

它通常是由地球的赤道（即连接北半球和南半球的圆弧）以及由两
个赤道之外的等圈组成的，两个等圈间的角度称为大圆度（准确的说是大圆偏移），大圆
度的基本单位是角度（秒）。

二、公法线的长度
公法线长度是指地球上两点之间的大圆距离，即从一点出发到另一点所经历的大圆弧
距离，通常单位是米（公尺）。

矩形坐标系统（例如经纬度）和圆形坐标系统（如公法线）之间的距离就是公法线长度。

公法线长度的长度取决于地球的周长，一般可以约定地球的
横径在4000公里左右，故公法线长度也接近4000公里。

三、公法线长度的极限偏差
由于地球表面存在着一定的曲面，所以在计算两点之间距离时，不能只考虑它们间的
直线距离，还需要受到地球曲面影响。

由于地球是一个琸球形，它的曲率不是均匀的，因此，地球表面上两个点的长度距离可能会和其直角距离大不相同，这就是所谓的偏差。

公
法线长度的极限偏差是指地球表面两点间的大圆距离的最大偏差，约为15米。

四、公法线长度的计算
计算公法线长度需要较大的计算量，一般使用计算机进行计算。

为此，需要根据地球
表面上两点的经纬度信息，然后使用一系列的计算公式，根据地球的曲度计算出两点的公
法线长度。

公法线计算公式公法线（Digitech's Rule）是用于天体观测中计算一个天体在天球上的位置和运动的工具。

它是由17世纪末德国天文学家Erhard Weigel 创立的，并由约翰内斯·哥白尼进一步发展和完善。

公法线的计算涉及到复杂的几何运算和三角学，并在现代天文学中仍然得到广泛应用。

公法线的计算基于地球绕太阳公转的基本原理。

地球的公转轨迹近似为一个椭圆，因此，太阳和地球之间的距离是不断变化的。

公法线主要用来计算天体在不同时刻的地心距离。

公法线的计算公式如下：R = P / (1 + e * cos(v))其中R是天体到地心的距离，P是椭圆轨道的半径，e是离心率，v 是真近点角。

首先，我们需要确定天体所在的椭圆轨道参数，包括轨道半径P和离心率e。

对于太阳和地球之间的距离，可以通过测量地球与天体之间的视差和知道地球的轨道参数来推算。

视差是指地球观测者在不同时间测量到的天体位置不同，从而得出的天体的地心距离。

对于太阳和地球之间的公法线，在给定时间 t 的地心距离 R 可以通过三角计算得到。

观测者可以观测到太阳和天体之间的角度，从而得到真近点角 v。

真近点角是天体距离椭圆轨道近日点的角度。

公法线的计算公式中的 cos(v) 是该角度的余弦值。

因为地球绕太阳的轨道是椭圆形的，离心率e大于零。

当e接近于零时，椭圆轨道趋近于一个圆，相应的公法线就趋近于一个常数。

而当e接近于1时，椭圆轨道趋近于一个长椭圆，相应的公法线就会有较大的变化。

公法线对于天文学研究非常重要。

通过测量地心距离，天文学家可以计算出天体的距离、运动速度等关键参数，从而研究天体的性质和运动。

公法线的计算为天文学研究提供了重要的工具，也使得科学家能够更好地理解地球和宇宙的运行规律。

需要注意的是，公法线的计算是一项复杂的几何运算和数学问题，需要借助计算机和专业软件进行计算。

科学家和天文学家通常会使用专门的软件来计算公法线，以确保精度和准确性。

公法线长度计算公式根据几何学原理，公法线为一个点到直线或曲线的垂直线段。

因此，公法线长度的计算取决于所给直线或曲线的方程形式。

对于直线：假设直线的方程为 y = mx + c，其中 m 是直线的斜率，c 是直线与y 轴的交点。

公法线的斜率是直线斜率的负倒数，即-1/m。

因此，公法线的方程为y=(-1/m)x+c'，其中c'是公法线与y轴的交点。

将两个方程相减，得到两条直线的交点为(x*,y*)，其中x*=(c'-c)/(m-1/m)，y*=m*x*+c。

然后，求解从交点到给定直线的垂直距离作为公法线的长度，即根据勾股定理计算((x*-x)^2+(y*-y)^2)^(1/2)。

对于曲线：假设曲线的方程为f(x)=y，其中f(x)是给定的曲线函数。

公法线的斜率是f'(x)的负倒数，即-1/f'(x)。

因此，公法线的方程为y=(-1/f'(x))*x+c'，其中c'是公法线与y轴的交点。

求解方程f'(x)=(-1/f'(x))*x+c'，得到两条曲线的交点为(x*,y*)。

然后，求解交点到给定曲线的垂直距离作为公法线的长度，即根据勾股定理计算((x*-x)^2+(y*-y)^2)^(1/2)。

需要注意的是，曲线的方程可能是复杂的，求解其斜率和交点可能需要使用微积分等高级数学方法。

以上是计算公法线长度的一般原理和方法。

对于具体的直线或曲线方程形式，需要根据方程的具体形式进行相应的数学推导和计算。

总结起来1.根据所给直线或曲线方程，计算出其斜率和与y轴的交点。

2.根据斜率的负倒数，得到公法线的方程。

3.求解公法线方程与原方程的交点坐标。

4.根据交点坐标和原点坐标，计算出公法线的长度（即垂直距离）。

需要注意的是，对于复杂的曲线方程，计算公法线长度可能需要使用高级数学方法，并不能简单地给出一个通用的计算公式。

因此，具体的计算方法和公式需要根据曲线的具体形式进行推导和计算。

公法线计算程序
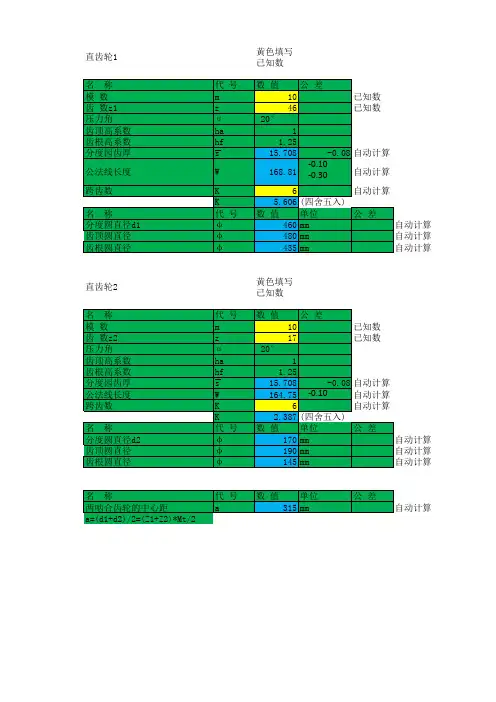
公法线长度计算公式：W=Wh+p/tan(Bp)。

其中W为公法线长度，Wh为齿高，p为跨测齿数，Bp为压力角。

以下是具体步骤：
1.将已知参数带入公式，可以得到另一个齿轮的模数。

2.利用双齿轮啮合传动的特点，可以得出新齿轮的分度圆直径、基圆直径、
中心距。

3.最后用标准值来计算其啮合的最大及最小宽度，并用和差模宽与平均模宽
之比来判断新齿轮的优劣。

在程序实现方面，一般可以通过使用C语言或Python语言来实现公法线计算。

需要调用相关的数学库，例如数学库或者numpy等。

这些库提供了一系列函数，如sin()、cos()、tan()等，以处理角度和进行计算。

在计算过程中，要注意考虑舍入误差的问题，使用合适的方法进行误差控制和计算结果的输出。

压力角30度齿轮公法线表
（实用版）
目录
1.压力角与齿轮的基本概念
2.30 度压力角齿轮的公法线公式
3.齿轮的基圆直径、分度圆直径和模数
4.30 度压力角齿轮公法线的应用实例
正文
一、压力角与齿轮的基本概念
在机械传动领域，齿轮是一种常见的传动装置。

齿轮的传动效率和磨损寿命与其压力角、齿数、模数等参数密切相关。

压力角是指齿轮齿廓线上任意一点处的法线与切线间的夹角，通常用来描述齿轮的齿廓形状。

二、30 度压力角齿轮的公法线公式
在齿轮设计中，公法线是一项重要的参数。

公法线是指齿轮的分度圆上，任意一点到齿轮基准圆的连线。

对于 30 度压力角的齿轮，其公法线公式如下：
公法线 = m * z
其中，m 为模数，z 为齿数。

三、齿轮的基圆直径、分度圆直径和模数
在齿轮的设计和制造过程中，齿轮的基圆直径、分度圆直径和模数都是重要的参数。

基圆直径是齿轮的基准圆直径，也是齿轮齿廓的起始圆直径。

分度圆直径是齿轮上每个齿所对应的圆直径。

模数是齿轮齿廓的高与齿距的比值，是一个无量纲的参数。

四、30 度压力角齿轮公法线的应用实例
在实际应用中，30 度压力角齿轮公法线被广泛应用于各种齿轮的设计和制造过程中。

例如，在设计一个 30 度压力角、齿数为 10、模数为 5 的齿轮时，可以先根据公法线公式计算出公法线的长度，然后根据公法线长度和其他参数进行齿轮的详细设计。

压力角30度齿轮公法线表【原创版】目录1.压力角 30 度齿轮的概念2.齿轮公法线公式3.齿轮的基圆直径、分度圆直径和压力角4.30 度压力角齿轮的优点5.结论正文一、压力角 30 度齿轮的概念压力角 30 度齿轮是一种在机械传动系统中应用广泛的齿轮类型。

它是指齿轮齿廓曲线上某一点的法线与齿轮齿廓曲线的切线之间的夹角为 30 度。

这种齿轮的齿廓曲线比较平缓，因此能够承受较大的载荷。

二、齿轮公法线公式齿轮公法线是指齿轮的分度圆上任意一点到齿轮基准圆的连线。

齿轮公法线公式如下：公法线 = m × z其中，m 为齿轮的模数，z 为齿轮的齿数。

三、齿轮的基圆直径、分度圆直径和压力角1.基圆直径：齿轮的基圆直径是齿轮的最小直径，通常用于确定齿轮的尺寸。

2.分度圆直径：齿轮的分度圆直径是齿轮上每个齿所对应的圆的直径，也称为节圆直径。

3.压力角：压力角是齿轮齿廓曲线上某一点的法线与齿轮齿廓曲线的切线之间的夹角。

压力角越大，齿轮的承载能力越强。

四、30 度压力角齿轮的优点1.承载能力强：与较小的压力角相比，30 度压力角齿轮的齿廓曲线更加平缓，因此能够承受更大的载荷。

2.传动比稳定：30 度压力角齿轮的齿廓曲线设计使得齿轮的传动比更加稳定，有利于提高机械传动系统的可靠性。

3.磨损小：30 度压力角齿轮的齿廓曲线更加平缓，因此齿轮在传动过程中的磨损较小，寿命较长。

五、结论压力角 30 度齿轮具有较强的承载能力、稳定的传动比和较小的磨损，因此在机械传动系统中得到了广泛的应用。

第1页共1页。

公法线长度计算公式
江庆辉;余梅
【期刊名称】《金属加工：冷加工》
【年(卷),期】2005(000)009
【总页数】2页(P52-53)
【作者】江庆辉;余梅
【作者单位】山东德隆集团机床有限责任公司,德州,253003;中国水利水电第十三工程局,山东,德州,253000
【正文语种】中文
【相关文献】
1.标准斜齿轮公法线长度的简易计算公式
2.DIN5480渐开线花键公法线长度和量棒测量值的计算
3.齿轮公法线长度参数化计算模型的研究与应用
4.齿轮公法线长度参数化计算模型的研究与应用
5.公法线长度测量在齿轮检测和测绘中的应用
因版权原因，仅展示原文概要，查看原文内容请购买。

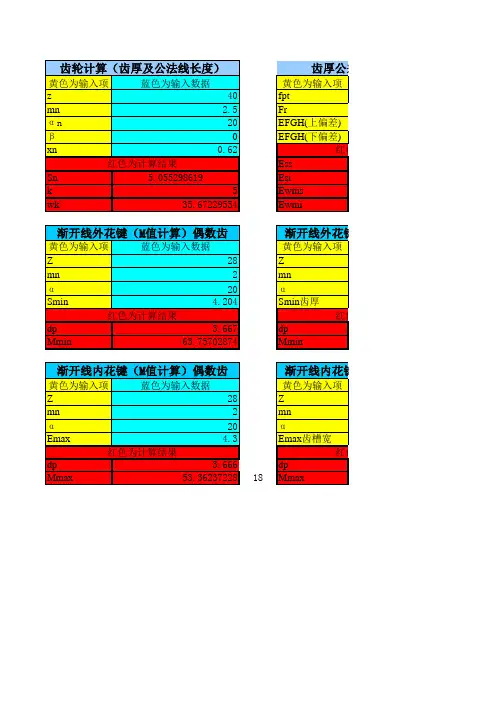
齿轮公法线上下偏差计算公式公法线平均长度上偏差Ews=Es*scosа-2e*sinа,公法线平均长度下偏差Ews=Esi*cosа+2e*sinа,公法线平均长度公差：Tw=Ts*cosа-4esinа,1、式中2e为齿轮一转内最大的几何偏心量，为ΔFr2e=ΔFr=KFr,根据国标取K=,式中Fr齿圈径向跳动公差有精度等级和分度圆直径决定（你未给出分度圆直径及应用，所以我没办法给你准确数，你自己查表）。

2、式中α为压力角，标准渐开线圆柱齿轮α=20°3、式中Ess和Esi为齿轮齿厚上偏差和下偏差，通常齿轮副，两齿轮的Ess 相同，Ess=fa*tagа+(jn min+J)/2cosа①式中fa为齿轮副中心距极限偏差，②式中jn min为齿轮副公法线方向极限侧隙，叫作法向极限侧隙，jn min=jn1+jn2jn1=a(α1Δt1+α2Δt2)*2sinа(单位mm)a---齿轮副中心距α1，α2---线膨胀系数（45#钢齿：*10^-6,铸铁箱体：*10^-6）Δt---工作温升（相对于20℃）脚注1为齿轮，脚注2为壳体jn2=K*mn （单位um)mn---法向模数系数K---5~10（油池润滑）10（V<10m/s)齿轮线速度(喷油润滑）20（10<V<25)30(25<v<60)30~50(V>60)Esi=Ess+TsTs=(Fr^2+br^2)^1/2*2tagαFr---齿圈径向跳动（查表）br---切齿径向进刀公差（查表）4、小结要得到公法线长度上下偏差必须根据应用环境来确定精度等级，有三组公差精度分别为：运动精度、平稳性精度、接触精度，示例一、7-6-6GM、示例二、7FL第一个示例表示运动精度7，平稳性精度和接触精度6，G和M代表齿厚上下偏差分别为-6fpt和-20fpt(买本书或下载齿轮手册上面有标准），fpt查表得，它属平稳性精度参数，第二个示例表示三组公差精度都为7，其他同上，只是齿厚公差带偏上一点了，F=-4fpt,L=-16fpt。

公法线和侧隙关系
公法线是描述齿轮齿廓与法线的交点之间的距离，而侧隙则是指齿轮在啮合过程中，为了防止卡死或过载而预留的空隙。

公法线与侧隙之间的关系可以用以下公式表示：
ΔE = ΔW / cosα
其中，ΔE表示侧隙，ΔW表示公法线微小变化量，α表示齿轮压力角。

这
个公式表明，公法线的微小变化量与侧隙的大小成正比，即公法线变化越大，侧隙也越大。

此外，中心距偏差也会影响侧隙。

如果中心距存在偏差，那么两齿轮的啮合中心距会产生偏差，进而导致啮合传动时有侧隙。

这类偏差属于第二类误差引起的偏差，主要来源于减速差速器的箱体两个平行孔之间的距离的偏差。

以上内容仅供参考，建议查阅齿轮设计、制造相关书籍或咨询专业人士以获取更准确的信息。

齿轮的公法线长度齿轮是一种常见的机械传动装置，广泛应用于各个领域。

在研究齿轮的特性和性能时，公法线长度是一个重要的指标。

本文将围绕齿轮的公法线长度展开讨论，介绍其概念、计算方法以及影响因素。

一、公法线长度的概念公法线长度是指齿轮齿面上两点之间的最短弧长，也可以理解为齿轮齿面曲线与公法面的交线的长度。

公法线长度是确定齿轮啮合性能的重要参数之一，它直接影响到啮合传动的平稳性、传动效率以及齿轮的寿命。

二、公法线长度的计算方法1. 近似计算法：根据齿轮的模数、齿数和压力角等基本参数，利用近似公式进行计算。

这种方法适用于一般情况下的齿轮计算，计算结果较为简便但精度有限。

2. 准确计算法：通过数学方法，根据齿轮齿面曲线的几何特性，进行精确计算。

这种方法适用于对齿轮公法线长度要求较高的特殊情况，计算结果更为准确。

三、公法线长度的影响因素1. 齿轮参数：齿轮的模数、齿数、压力角等参数会直接影响到公法线长度。

一般情况下，齿数越多、模数越小、压力角越小，公法线长度越大。

2. 齿轮啮合方式：不同的啮合方式会导致公法线长度的变化。

例如，直齿轮的公法线长度相对较短，而斜齿轮的公法线长度相对较长。

3. 齿轮加工精度：齿轮的加工精度直接影响到公法线长度的准确性。

加工精度越高，公法线长度越接近设计值。

4. 齿轮材料和磨损情况：不同材料的齿轮在使用过程中会出现不同程度的磨损，从而影响到公法线长度。

磨损越严重，公法线长度越大。

四、公法线长度的意义和应用1. 齿轮传动的平稳性：公法线长度的大小直接影响到齿轮传动的平稳性。

公法线长度越大，齿轮啮合时的冲击和振动越小，传动平稳性越好。

2. 传动效率：公法线长度的大小也会对齿轮传动的效率产生影响。

公法线长度越短，齿轮的传动效率越高。

3. 齿轮寿命：公法线长度对齿轮的寿命也有重要影响。

公法线长度越小，齿轮的接触应力越大，容易导致齿面疲劳破坏，从而影响到齿轮的寿命。

总结：本文围绕齿轮的公法线长度展开讨论，介绍了其概念、计算方法以及影响因素。

公法线的计算公式公法线，这听起来好像是个有点陌生又有点神秘的概念，对吧？其实啊，公法线在机械工程和齿轮传动的领域里可是相当重要的呢！先来说说啥是公法线。

公法线就是指在两个相互啮合的齿轮上，跨越若干个齿的两个异侧齿廓的公共法线。

简单点儿说，就是一条在齿轮上很关键的线。

那公法线的计算公式是啥呢？公法线长度的计算公式是：W = m ×cosα × [π×(k - 0.5) + z × invα] 。

这里面的 m 是齿轮的模数，α 是压力角，k 是跨齿数，z 是齿数，invα 是压力角的渐开线函数。

哎呀，别一看到这一堆公式和符号就头疼。

我给您举个例子哈。

就说有个小机械厂，里面的师傅们正在加工一批齿轮。

其中有个年轻的小徒弟，就被这公法线的计算给难住了。

师傅过来一看，笑了笑说：“别着急，咱们一步步来。

”师傅拿起图纸，指着上面的参数说：“你看啊，这模数是 3，齿数是 20，压力角是 20 度，咱们先算算跨齿数。

”小徒弟眨眨眼睛，一脸认真地听着。

师傅接着说：“跨齿数可以用这个公式算，k = z × α / 180 + 0.5 ，算出来跨齿数是 3 。

”然后师傅带着小徒弟，把数字一个个代入公法线长度的公式里，一点点计算。

小徒弟边看边点头，恍然大悟：“原来也没那么难嘛！”在实际的工程应用中，准确计算公法线的长度非常重要。

如果计算不准确，齿轮之间的啮合就可能出问题，要么运转不顺畅，要么磨损得特别快。

所以说，这公法线的计算公式可得掌握好咯。

再深入想想，这公法线的计算其实也反映了数学和工程实践的紧密结合。

数学公式看起来可能枯燥，但在解决实际问题的时候，那可真是威力无穷。

您瞧，无论是大型的机械制造，还是小小的零件加工，公法线的计算都像是一个精准的指南，指引着工程师们打造出完美运转的齿轮系统。

总之，公法线的计算公式虽然有点复杂，但只要咱们耐心琢磨，多实践多练习，就能熟练掌握，为各种机械设计和制造提供准确可靠的支持。

两个圆相接触的公法线
公法线是物理术语，意思是两个曲线或曲面，过特定点，拥有共同的一条垂线，这条垂线就是公法线。

两个曲线或曲面，通过特定点，拥有共同的一条垂线，这条垂线就是公法线。

对于齿轮，相邻几个轮齿两外侧渐开线齿廓的公共法线。

公法线长度是一条与基圆相切的直线同时跨过几个齿轮时，直线上某两齿廓外侧间的距离。

测绘时标注出公法线长度为检验齿轮齿厚尺寸提供了准确的依据，公法线长度一般使用公法线千分尺测量，在实践中相对来说比较方便，经济。

它综合反映了齿轮模数，齿数，压力角，变位系数等有关参数是齿轮测绘中最主要的标注参数。

公法线长W为两平行平面与齿轮轮齿两异名齿面相切的两切点
间的直线距离。

测量时，使用公法线长度千分尺，它的两个测量面应与渐开线齿形面相切于齿轮的分度圆附近。

同时必须在齿轮圆周均匀分布的4个位置上进行测量，并取其4次测量的平均值，在公差范围内即为合格。

公法线长度变动是指在同一齿轮上公法线的最大长度与最小长度之差。

测量时必须在齿轮的整个圆周上逐步依次进行测量，才能测出公法线长度的最大和最小值。

用公式表示式中，max——公法线长度的最大值；min——公法线长度的最小值。

公法线长度计算以此次320改造为例，Ⅰ齿Step1. 跨测齿数k《机修手册》第一卷（下册）P11-152表11-6-3 公法线长度跨测齿数k 的计算公式0.111110.5=0.11111360.55k Z =+⨯+≈（四舍五入）Step2. 公法线长度W《机修手册》第一卷（下册）P11-156表11-6-5 直齿轮公法线长度根据跨测齿数k=5和齿轮齿数Z=36，查上表，得到模数m=1，压力角=20α的公法线长度5=13.7888W ；那么模数m=7的公法线长度5=7W =96.5216W ⨯。

Step3. 最终公法线长度W 及公法线长度公差min =()sW n SS T W W F j E ----最终公法线①. 《机修手册》第一卷（下册）P11-264表11-9-25 公法线长度变动公差W F 值根据精度等级：6级精度；分度圆直径区间：125252400<≤mm 。

查得：0.025W F mm =。

②. 《机修手册》第一卷（下册）P11-265表11-9-27 最小法向极限侧隙min n j根据侧隙种类：d 类；中心距231a =，180231250<≤mm 。

查得：min 0.072n j mm =。

③. 《机修手册》第一卷（下册）P11-267表11-9-29 齿厚上偏差ss E根据侧隙种类：d 类；法向模数m=7，1710≤≤；分度圆直径区间：250252315<≤mm ；精度等级：6级精度。

查得：0.063ss E mm =。

④. 《机修手册》第一卷（下册）P11-269根据精度等级：6级精度；法向模数m=7，1710≤≤；分度圆直径区间：250252315<≤mm 。

查得：0.080S T mm =。

那么：0min =()s W n SS T W W F j E ----最终公法线00.0800.08=(96.520.0250.0720.063)96.36W -----=。