公法线长度定义

公法线长度及其极限偏差
一、什么是公法线
公法线，也称为公坐标系统（GCC），是一种特殊的度量标准，用来衡量地球表面两
个点间的距离和方位。

它通常是由地球的赤道（即连接北半球和南半球的圆弧）以及由两
个赤道之外的等圈组成的，两个等圈间的角度称为大圆度（准确的说是大圆偏移），大圆
度的基本单位是角度（秒）。

二、公法线的长度
公法线长度是指地球上两点之间的大圆距离，即从一点出发到另一点所经历的大圆弧
距离，通常单位是米（公尺）。

矩形坐标系统（例如经纬度）和圆形坐标系统（如公法线）之间的距离就是公法线长度。

公法线长度的长度取决于地球的周长，一般可以约定地球的
横径在4000公里左右，故公法线长度也接近4000公里。

三、公法线长度的极限偏差
由于地球表面存在着一定的曲面，所以在计算两点之间距离时，不能只考虑它们间的
直线距离，还需要受到地球曲面影响。

由于地球是一个琸球形，它的曲率不是均匀的，因此，地球表面上两个点的长度距离可能会和其直角距离大不相同，这就是所谓的偏差。

公
法线长度的极限偏差是指地球表面两点间的大圆距离的最大偏差，约为15米。

四、公法线长度的计算
计算公法线长度需要较大的计算量，一般使用计算机进行计算。

为此，需要根据地球
表面上两点的经纬度信息，然后使用一系列的计算公式，根据地球的曲度计算出两点的公
法线长度。

公法线长度表是大地测量学中的重要工具，用来计算地球表面上两点之间的直线距离。

公法线是指地球上某个经度上的曲线，其切线方向就是该点处的南北向。

是以公里为单位的一种距离测量工具，具有精度高、可靠性好等优点，被广泛应用于地球物理勘探、地图制作、航空航海等领域。

的起源可以追溯到18世纪，当时法国学者拉普拉斯为了解决天文测量中的问题，提出了公法线距离测量的概念，并提出了一种具体的计算方法。

随着时间的推移，这种方法不断得到改进和完善，最终形成了的现代版本。

的计算方法基于大地测量学中的基本原理，即地球的曲率半径在不同地点有所不同，因此两个点之间的直线距离需要以曲线距离来计算。

在实际计算中，需要先确定两点之间的经度差，然后根据所处经度所对应的大地曲率半径来计算两点间的曲线距离。

最终，通过对每个经度差进行累加，就可以得到两点之间的公法线长度。

具有非常高的准确度和精度，其计算结果可以达到毫米级别的精度。

这一点非常重要，因为在现代社会中，很多行业都需要进行高精度地测量，如建筑工程、地理信息系统、电力勘探等。

的出现，可以大大提高这些行业的工作效率和测量精度。

除了在现代工程技术领域应用外，在历史上也发挥了重要作用。

在18世纪欧洲，许多国家都在进行地图制作和领土划定工作，而公法线距离测量方法则成为了当时最为流行的一种测量方式。

由于当时各国之间的地图标准不一致，因此需要一个能够统一测量单位和标准的工具，就成为了当时的最佳选择。

总之，是一项非常重要的大地测量学成果，它不仅能够提高现代工程技术领域的工作效率和精度，也是历史上一项非常重要的测量工具。

随着科学技术的不断进步，的精度和应用范围还将得到进一步提高。

公法线长度与齿厚关系（原创实用版）目录1.公法线长度与齿厚的概念2.公法线长度与齿厚的关系3.齿厚的测量方法4.公法线长度变动偏差与公法线平均长度偏差的关系5.测量公法线长度在齿轮制造中的应用6.结论正文一、公法线长度与齿厚的概念公法线长度是指齿轮上任意一点到齿顶圆的连线，在齿轮制造中，它是一个重要的参数。

齿厚是齿轮齿廓的厚度，也是齿轮制造中的一个关键参数。

在齿轮的设计和制造过程中，公法线长度和齿厚有着密切的关系。

二、公法线长度与齿厚的关系齿厚上下偏差与公法线上下偏差有对应关系。

公法线平均长度及偏差，就是控制齿厚的。

换句话说，公法线长度的变动可以直接影响到齿厚的精度。

因此，在齿轮的制造过程中，通过控制公法线的长度，可以有效地控制齿厚的精度。

三、齿厚的测量方法齿厚的测量方法有很多，其中常用的、比较准确的测量方法是使用齿厚计。

这种测量方法的精度较高，可以满足大部分齿轮制造过程中的精度要求。

另外，固定弦齿厚也是测量、控制齿厚的一种方法，它需要借助齿顶圆，精度稍差，适于模数很大的齿轮。

四、公法线长度变动偏差与公法线平均长度偏差的关系公法线长度变动偏差可以度量齿距误差，而公法线平均长度偏差可以度量齿厚（及偏差）。

因此，公法线长度变动偏差与公法线平均长度偏差之间存在着直接的关系。

五、测量公法线长度在齿轮制造中的应用测量公法线长度是渐开线圆柱齿轮控制齿厚的常用方法，对变位齿轮同样适用。

在齿轮的制造过程中，通过测量公法线长度，可以有效地控制齿轮的齿厚，从而保证齿轮的精度。

六、结论公法线长度与齿厚在齿轮制造过程中有着密切的关系。

通过控制公法线长度，可以有效地控制齿厚的精度，从而保证齿轮的质量。

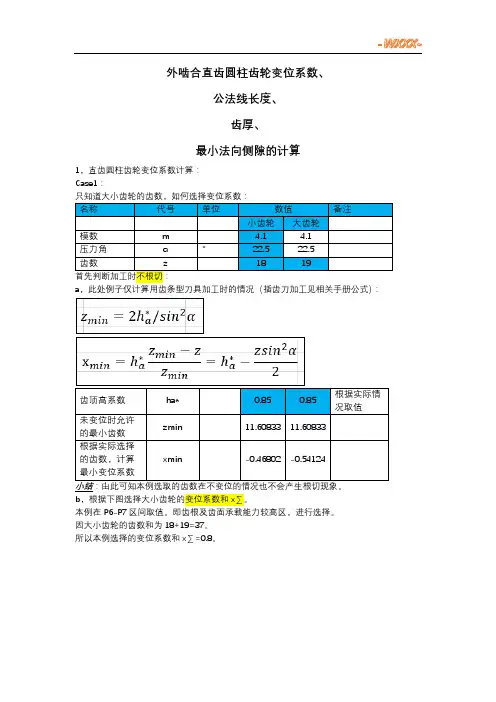
外啮合直齿圆柱齿轮变位系数、公法线长度、齿厚、最小法向侧隙的计算1，直齿圆柱齿轮变位系数计算：Case1：a，此处例子仅计算用齿条型刀具加工时的情况（插齿刀加工见相关手册公式）：小结：由此可知本例选取的齿数在不变位的情况也不会产生根切现象。

b，根据下图选择大小齿轮的变位系数和x∑。

本例在P6-P7区间取值。

即齿根及齿面承载能力较高区，进行选择。

因大小齿轮的齿数和为18+19=37。

所以本例选择的变位系数和x∑=0.8。

本例我们的两个齿轮在工作时属于减速运动，所以按减速运动的变位系数分配线图，进行2个齿轮的变位系数的选择。

先按(z1+z1)/2=18.5，作为横坐标，做一条垂线（图中蓝色的线），再按x∑/2=0.4，作为纵坐标，做一条水平线（图中橙色的线），接着沿着L线的趋势，穿过上面2条线的交点做一条射线（图中红色的线）最后按大小齿轮的齿数做相应的垂线（图中紫色的线），即得到需要的各自变位系数。

最后我们选择的变位系数即为：小齿轮x1=0.42，大齿轮x2=0.38。

【基本保障其和与之前x ∑一致，即可】。

c，验算变位后的齿顶厚度：注：一般要求齿顶厚Sa≥0.25m；对于表面淬火的齿轮要求Sa≥0.4m下表中的da的计算见后面的计算表格中的计算公式（因为当齿轮变位后，齿顶圆的计算和未变位齿轮的计算稍有差别-涉及到变位系数和中心距变位系数。

）。

分度圆直径db mm 73.8 77.9齿轮的齿顶圆直径da mm 83.027 86.799齿轮的齿顶压力角αa °27.27 26.17中间值invα0.0215 0.0215中间值invαa 0.0587 0.0347齿顶厚Sα 5.77 7.47判断值0.25m 1.025 1.025判断值0.4m 1.64 1.64小结：计算发现变位后的齿轮齿顶厚满足设计需求。

根据上面确定的变位系数，计算齿轮的中心距变位系数和节圆直径、齿根圆直径、齿顶圆直径。

公法线长度计算公式根据几何学原理，公法线为一个点到直线或曲线的垂直线段。

因此，公法线长度的计算取决于所给直线或曲线的方程形式。

对于直线：假设直线的方程为 y = mx + c，其中 m 是直线的斜率，c 是直线与y 轴的交点。

公法线的斜率是直线斜率的负倒数，即-1/m。

因此，公法线的方程为y=(-1/m)x+c'，其中c'是公法线与y轴的交点。

将两个方程相减，得到两条直线的交点为(x*,y*)，其中x*=(c'-c)/(m-1/m)，y*=m*x*+c。

然后，求解从交点到给定直线的垂直距离作为公法线的长度，即根据勾股定理计算((x*-x)^2+(y*-y)^2)^(1/2)。

对于曲线：假设曲线的方程为f(x)=y，其中f(x)是给定的曲线函数。

公法线的斜率是f'(x)的负倒数，即-1/f'(x)。

因此，公法线的方程为y=(-1/f'(x))*x+c'，其中c'是公法线与y轴的交点。

求解方程f'(x)=(-1/f'(x))*x+c'，得到两条曲线的交点为(x*,y*)。

然后，求解交点到给定曲线的垂直距离作为公法线的长度，即根据勾股定理计算((x*-x)^2+(y*-y)^2)^(1/2)。

需要注意的是，曲线的方程可能是复杂的，求解其斜率和交点可能需要使用微积分等高级数学方法。

以上是计算公法线长度的一般原理和方法。

对于具体的直线或曲线方程形式，需要根据方程的具体形式进行相应的数学推导和计算。

总结起来1.根据所给直线或曲线方程，计算出其斜率和与y轴的交点。

2.根据斜率的负倒数，得到公法线的方程。

3.求解公法线方程与原方程的交点坐标。

4.根据交点坐标和原点坐标，计算出公法线的长度（即垂直距离）。

需要注意的是，对于复杂的曲线方程，计算公法线长度可能需要使用高级数学方法，并不能简单地给出一个通用的计算公式。

因此，具体的计算方法和公式需要根据曲线的具体形式进行推导和计算。

公法线长度偏差定义标题：探究公法线长度偏差定义：从基本概念到深入解析前言：在几何学和测量学中，公法线长度偏差是一个关键术语，其定义和理解对于正确评估物体的形状和尺寸至关重要。

本文将从基本概念开始，逐步深入地探讨公法线长度偏差的定义及其重要性，并分享个人观点和理解。

第一部分：基本概念和定义1. 什么是公法线长度偏差？公法线长度偏差是用于描述曲线与其对应切线（公法线）之间的长度差异的概念。

它衡量了曲线在某一点的切线段与实际曲线段之间的差异，它是判定曲线形状是否趋于光滑的重要指标之一。

2. 公法线长度偏差的计算方法公法线长度偏差的计算方法通常涉及连续微积分和相应的数学模型。

一种常见的计算方法是使用曲线的参数方程，并利用导数来计算曲线在每一点的切线长度。

通过将切线长度与实际曲线长度进行比较，我们可以得到公法线长度偏差的数值。

第二部分：公法线长度偏差的重要性1. 公法线长度偏差在几何建模中的应用公法线长度偏差在几何建模中扮演着关键角色。

通过评估曲线的公法线长度偏差，我们可以检查曲线的光滑程度和精度，这对于涉及复杂形状和曲线的工程项目、艺术设计和数字化建模是至关重要的。

2. 公法线长度偏差对产品质量的影响在制造业中，公法线长度偏差的定义对于确保产品质量至关重要。

通过控制公法线长度偏差，我们可以评估产品的尺寸精度和形状准确性，从而确保产品符合设计要求，并满足客户的期望和需求。

第三部分：个人观点和理解1. 公法线长度偏差的灵活性和应用广度公法线长度偏差的定义和应用是多样化和广泛的。

它不仅可以用于评估曲线的光滑程度，还可以用于测量各种复杂形状的尺寸精度。

在当今快速发展的科技领域，公法线长度偏差的概念也被广泛应用于3D打印、机器人技术和虚拟现实等领域。

2. 公法线长度偏差与人类感知的关系我相信，公法线长度偏差的定义和评估与人类感知密切相关。

公法线长度偏差的小幅度变化可能会对人类感知形状和质量的判断产生重要影响。

准确理解和评估公法线长度偏差对于更好地满足人类需求和提高用户体验至关重要。

公法线的定义：
A 公法线就是两个齿轮分度圆（变位后节圆）的公切线与两个啮合齿轮的中心线垂直
B 渐开线齿轮的公法线长度是指与两个异侧齿面相切的两平行平面间的距离W。

通常用测量公法线长度的方法来检验齿轮的精度，既简便又准确，同时避免了采用齿顶圆作为测量基准而造成齿顶圆精度的无谓提高。

公法线的影响：
一、公法线偏大的影响
1、渐开线轮廓线加工误差会产生明显的干涉，严重的不能构成理想的接触纯滚动，造成的结果是：啮合运行时，齿面在不同区域产出相对滑移
2、在齿轮设计和加工中，渐开线曲面一般都没有“面轮廓度”的限定，但实际上，面轮廓度是随加工精度的不同而发生区域性不确定变化的，这将导致传动的瞬时突变，传动比瞬时不准，载荷的瞬时突变
3、在润滑不良的前提下，运行粗暴、产生瞬时冲击的附加载荷、以及噪音等将会随之发生
二、公法线偏小的影响
公法线偏小将直接导致齿侧隙将变大，随之产生的不良结果有：
1、系统若是交变载荷时，将会导致反向冲击
2、在交变载荷下，瞬时传动比失准
3、若是单项载荷，上述两项将被忽略，但轮齿强度较之公法线偏大状态有偏弱趋向
4、对润滑的要求没有公法线偏大的齿轮强
5、运行噪音小。

齿轮的公法线长度齿轮是一种常见的机械传动装置，广泛应用于各个领域。

在研究齿轮的特性和性能时，公法线长度是一个重要的指标。

本文将围绕齿轮的公法线长度展开讨论，介绍其概念、计算方法以及影响因素。

一、公法线长度的概念公法线长度是指齿轮齿面上两点之间的最短弧长，也可以理解为齿轮齿面曲线与公法面的交线的长度。

公法线长度是确定齿轮啮合性能的重要参数之一，它直接影响到啮合传动的平稳性、传动效率以及齿轮的寿命。

二、公法线长度的计算方法1. 近似计算法：根据齿轮的模数、齿数和压力角等基本参数，利用近似公式进行计算。

这种方法适用于一般情况下的齿轮计算，计算结果较为简便但精度有限。

2. 准确计算法：通过数学方法，根据齿轮齿面曲线的几何特性，进行精确计算。

这种方法适用于对齿轮公法线长度要求较高的特殊情况，计算结果更为准确。

三、公法线长度的影响因素1. 齿轮参数：齿轮的模数、齿数、压力角等参数会直接影响到公法线长度。

一般情况下，齿数越多、模数越小、压力角越小，公法线长度越大。

2. 齿轮啮合方式：不同的啮合方式会导致公法线长度的变化。

例如，直齿轮的公法线长度相对较短，而斜齿轮的公法线长度相对较长。

3. 齿轮加工精度：齿轮的加工精度直接影响到公法线长度的准确性。

加工精度越高，公法线长度越接近设计值。

4. 齿轮材料和磨损情况：不同材料的齿轮在使用过程中会出现不同程度的磨损，从而影响到公法线长度。

磨损越严重，公法线长度越大。

四、公法线长度的意义和应用1. 齿轮传动的平稳性：公法线长度的大小直接影响到齿轮传动的平稳性。

公法线长度越大，齿轮啮合时的冲击和振动越小，传动平稳性越好。

2. 传动效率：公法线长度的大小也会对齿轮传动的效率产生影响。

公法线长度越短，齿轮的传动效率越高。

3. 齿轮寿命：公法线长度对齿轮的寿命也有重要影响。

公法线长度越小，齿轮的接触应力越大，容易导致齿面疲劳破坏，从而影响到齿轮的寿命。

总结：本文围绕齿轮的公法线长度展开讨论，介绍了其概念、计算方法以及影响因素。

公法线的计算公式公法线，这听起来好像是个有点陌生又有点神秘的概念，对吧？其实啊，公法线在机械工程和齿轮传动的领域里可是相当重要的呢！先来说说啥是公法线。

公法线就是指在两个相互啮合的齿轮上，跨越若干个齿的两个异侧齿廓的公共法线。

简单点儿说，就是一条在齿轮上很关键的线。

那公法线的计算公式是啥呢？公法线长度的计算公式是：W = m ×cosα × [π×(k - 0.5) + z × invα] 。

这里面的 m 是齿轮的模数，α 是压力角，k 是跨齿数，z 是齿数，invα 是压力角的渐开线函数。

哎呀，别一看到这一堆公式和符号就头疼。

我给您举个例子哈。

就说有个小机械厂，里面的师傅们正在加工一批齿轮。

其中有个年轻的小徒弟，就被这公法线的计算给难住了。

师傅过来一看，笑了笑说：“别着急，咱们一步步来。

”师傅拿起图纸，指着上面的参数说：“你看啊，这模数是 3，齿数是 20，压力角是 20 度，咱们先算算跨齿数。

”小徒弟眨眨眼睛，一脸认真地听着。

师傅接着说：“跨齿数可以用这个公式算，k = z × α / 180 + 0.5 ，算出来跨齿数是 3 。

”然后师傅带着小徒弟，把数字一个个代入公法线长度的公式里，一点点计算。

小徒弟边看边点头，恍然大悟：“原来也没那么难嘛！”在实际的工程应用中，准确计算公法线的长度非常重要。

如果计算不准确，齿轮之间的啮合就可能出问题，要么运转不顺畅，要么磨损得特别快。

所以说，这公法线的计算公式可得掌握好咯。

再深入想想，这公法线的计算其实也反映了数学和工程实践的紧密结合。

数学公式看起来可能枯燥，但在解决实际问题的时候，那可真是威力无穷。

您瞧，无论是大型的机械制造，还是小小的零件加工，公法线的计算都像是一个精准的指南，指引着工程师们打造出完美运转的齿轮系统。

总之，公法线的计算公式虽然有点复杂，但只要咱们耐心琢磨，多实践多练习，就能熟练掌握，为各种机械设计和制造提供准确可靠的支持。

公法线长度
科技名词定义
中文名称：公法线长度
英文名称：base tangent length
定义：对于外齿轮,指相隔若干个齿的两外侧齿面各与两平行平面中的一个平面相切，此两平行平面之间的垂直距离。

对于内齿轮，指相隔若干个齿槽的两外侧齿面。

所属学科：机械工程（一级学科)；传动（二级学科）；齿轮传动（三级学科）
本内容由全国科学技术名词审定委员会审定公布
渐开线齿轮的公法线长度是指与两个异侧齿面相切的两平行平面间的距离W。

对直齿圆柱齿轮,公法线长度的公称值W按下式计算:
W=mcosα［π（k-0.5)+zinvα］+2xminvα
α＝20 °时
W＝m［2．9521（k—0．5）+0．014006z］+0．68404xm
式中 m 模数；
a 齿形角；
z 齿数；
x 变位系数；
k 跨齿数。

齿轮测量:。

公法线长度计算范文公法线长度指的是一国境内公路网的总长度，包括高速公路、国道、省道、县道等各级道路的总和。

公法线长度的计算对于交通规划、资源调配等具有重要的参考价值。

本文将介绍公法线长度计算的方法，并对其应用进行简要分析。

直接测量法一般采用全线测量法或地理信息系统（GIS）测量法。

全线测量法是指利用测量仪器和设备对各级道路进行测量，包括直线段和曲线段的测量，通过累加测得的各段长度来计算总长度。

GIS测量法则是利用遥感技术、GPS定位等手段，获取道路坐标数据后进行测量。

这两种方法都需要耗费大量人力、物力和时间，适用于小范围的道路测量。

间接统计法则是收集各级道路的长度数据，通过统计计算得出公法线长度。

这种方法相对简单、高效，并且可以得到较准确的结果。

具体的流程包括：1.收集各级道路长度数据：通过相关机构、部门提供的数据，或者通过公开的交通规划文件、统计年鉴等信息源获取各级道路的长度数据。

2.整理数据：将收集到的不同级别的道路长度数据进行整理和分类，确定各级道路的长度。

3.去重处理：在整理数据的过程中，可能会出现不同数据源中道路长度的重复或冲突情况，需要进行去重处理，确保数据的准确性。

4.统计计算：根据整理好的数据，对各级道路的长度进行统计计算，累加得到总长度。

5.验证和核对：根据计算出的结果，与其他相关数据进行对比和核对，确保计算结果的准确性。

公法线长度的应用主要体现在交通规划和资源调配方面。

通过公法线长度的计算，可以了解一个国家或地区的交通发展状况和现状，为交通规划提供依据。

同时，公法线长度也是交通资源分配的重要依据，可以用于评估各地区的道路需求和资源分布，合理配置交通资源。

此外，公法线长度也是交通运输行业的重要指标之一，对于交通行业的监管和管理具有重要意义。

总之，公法线长度的计算是一项复杂而重要的任务，涉及到数据收集、统计计算、核对验证等多个环节。

通过合理选择测量方法和严格的数据整理、处理，可以得出准确的公法线长度结果，为交通规划和资源调配提供科学依据。

齿轮公法线它被用来确定两个齿轮啮合的间隙，比如说一对标准直齿圆柱齿轮，分度圆直径和公法线长度可以直接确定这对齿轮的中心距。

另外，它也是确定齿条或凸轮轴相对位置的重要参数。

本文就齿轮公法线与齿条及凸轮轴的相关问题进行简单的探讨。

在我们的现实生活中，经常遇到这样的问题：汽车发动机上为什么会有一根直的金属导轨？就是为了确定齿轮（或者凸轮）与发动机的相对位置；工厂里，为什么在加工一些零件时要把一些圆柱形的零件顶尖磨平，这就是为了保证齿轮（或者凸轮）的相互位置；而一些齿轮与齿轮啮合时需要确定其齿数，或某一特定尺寸时，为了找出齿数与齿轮相应尺寸之间的关系，同样要用到公法线。

那么公法线究竟是怎么回事呢？为了解决这个问题，我查阅了有关资料。

中学物理课本里面讲到这个问题，指的是两个不同齿数的齿轮要想能够正常啮合并且不脱落，则两齿轮的轴线必须保持平行，否则，齿轮就无法正常啮合，甚至还会产生冲击，因此，要想保证两个齿轮能正常啮合并且不脱落，则必须保证两齿轮的轴线必须保持平行。

也就是说，当把齿轮转到啮合点的时候，它们之间的连线即为公法线。

如果没有公法线，齿轮就不能正常啮合。

而公法线的存在使得两齿轮的轴线保持平行，从而达到了“正常啮合”的效果。

1、如果没有了公法线，齿轮（或者凸轮）与发动机的相对位置会发生改变。

可能是方向相反，这时，发动机可能会运转不稳定；可能是方向相同，这时，发动机的力量会不足。

因此，有了公法线，齿轮才能够“正常啮合”。

2、有些螺旋线是假象，其实根本不存在。

比如说：有一种螺旋齿刀具，它虽然在电脑模拟显示屏上看上去似乎像螺旋线，但实际上并不存在，只不过电脑显示屏把它表现成这种状态罢了。

所以，在分析问题时，不要轻易被假象迷惑了。

3、在直角三角形中，各边上的中线把它们垂直于纸面放置时，其角度叫做三角形的倾斜角，这时，斜边的长度就是公法线长度。

注意，公法线长度只跟两边的夹角有关，跟两边的长短没有关系。

总之，公法线起着极其重要的作用。

和两个非对应齿面相切的两个平行平面之间的距离称为公法线长度。

是齿轮的k个齿之间的与两渐开线面相切的平行平面间距离,---------k为公法线跨齿数一般取分度圆上的相应两点作为测量距离
直齿轮(分度圆压力角20度,齿顶高系数ha为1)
跨齿轮数k=20/180*Z+0.5若是小数,取大于小数的最近整数,,如1.1取2
公法线长度Wk=m(2.9521(k-0.5)+0.014Z)
既然是普通的斜齿轮，那么压力角αn=20°我们可以求出端面压力角αt
tgαt=tgαn/tgβ=0.3768097 β为螺旋角
αt=20.646896°
则相当齿数Z\1=Z ×invαt/invαn=84×0.016453÷0.0149044=92.73
invαt/invαn为查表求得见机械原理之类的书
跨齿数K=0.111 Z\1+0.5 带入数值德K=10.8 取整K=11
公法线长度为
W=m[2.9521(K-0.5)+0.014 Z\1]=2[2.9521(11-0.5)+0.014*92.73]=64.6。

谈谈对《机械设计手册》上“公法线长度表”的看法中煤北京煤机公司退休职工 周万峰摘要：手册上的“公法线长度表”中将“基圆弧长”说成是“公法线长度”是不合理的。

本文对此进行了分析和论证，并给出了公法线长度计算的合理选择用表。

关键词：公法线长度，基圆弧长。

1、将“基圆弧长”说成是“公法线长度”是不合理的2005年4月间一个偶然的机会笔者看到了化工出版社2002年新修订出版的《机械设计手册》。

然而新手册对“公法线长度表”中原有的某些不合理之处并未有所改变，仍称k 对应的**kn W W (）“为1=m （或)1=n m 的标准齿轮的公法线长度”（见表1）。

笔者认为这种说法是不合理的。

今从新手册的“公法线长度表”中随意取z=50这个齿数进行分析，看看它的说法为什么是不合理的。

大家知道，公法线长度有合理与否的问题。

所谓合理，就是说公法线的测量点（量具卡脚与齿廓的切点）应在齿高的中点部位。

因为在这个部位测出的公法线长度比较准确。

所谓不合理，就是说公法线的测量点在齿顶部或齿根部了。

因为在这个部位公法线长度测量不准，影响齿厚的精度。

如果测量点在齿顶圆之外或齿根圆以内，那就说明这条线段已不是公法线长度了；因为测量点不在渐开线齿廓上，无法测量。

这些论点都是大家所公认的。

现在就根据大家所公认的论点，对表1中的跨齿数k 对应的“公法线长度”进行验证，看看它们是否都是公法线长度。

表1 公法线长度*W020 1====n n m m αα， 齿数z ' 跨齿数k公法线长度*W 50 411.0327 513.9849 616.9370 719.8891 822.8413 9 25.7934注：表1是从《机械设计手册》 （2002年化工出版社）上节录的。

表2 基 圆 弧 长 *L1==n m m ，020==n αα 齿 数变 位 系 数 跨（含）齿数 基圆弧长 z 'x k *L50 ＞︱0.745︱～︱1.804︱ 4 11.0327 ＞︱0.299︱～︱0.745︱ 5 13.9849 ＜︱0.299︱～0.2666 16.9370 ＞0.266～0.9637 19.8891 ＞0.963～1.8088 22.8413 ＞1.808～2.823 9 25.7934注：① 表2是笔者根据表1改造的。

公法线长度的基本尺寸
公法线长度，即公制计量单位之间的转换，是维护质量和准确性的重
要标准。

公法线长度可以定义为一个国家或地区规定用于测量长度和距离
的基本尺寸。

在美国，公法线长度由国家计量局（NIST）定义为米或英尺。

在这种情况下，一米等于3.2808398950131英尺，而一英尺等于0.3048米。

公法线长度也可以用于把其他计量单位转换成米或英尺，以确保准确
测量。

例如，一公里等于1000米，约等于3280.8398950131英尺；一英
里等于1609.344米，约等于5280英尺。

除了米和英尺，其他常用的公法线长度还有英寸、厘米、千米、里程等。

一英寸等于2.54厘米，一千米等于1000米，一里程等于1.609公里。

此外，公法线长度也可以应用于实际场景，例如路的宽度、桥的长度
和建筑的高度都需要使用公法线长度来准确计算和参考。

公法线长度计算式公法线的长度计算式可以通过下列步骤推导得到：1.首先，我们需要了解公法线的定义。

公法线是从一个点到一些曲线的垂直线段，它与该曲线相切于该点。

公法线的长度可以通过测量该垂直线段的长度来确定。

2.假设我们有一个曲线的方程为y=f(x)，其中f(x)是x的函数。

我们想要计算曲线上其中一点(x1,y1)处的公法线长度。

3.公法线是与曲线相切的直线，因此我们可以通过求解曲线和公法线的斜率相等来找到公法线的具体方程。

假设公法线的斜率为m，那么曲线在点(x1,y1)处的切线的斜率为f'(x1)（即f(x)关于x的导数在x=x1的值）。

4.我们知道切线的方程可以表示为y-y1=m(x-x1)。

将切线的斜率替换为f'(x1)得到y-y1=f'(x1)(x-x1)。

现在我们需要找到公法线的方程。

5.考虑到公法线与切线垂直，我们知道公法线的斜率是切线斜率的负倒数。

所以，公法线的斜率为-1/f'(x1)。

6.将公法线的斜率替换切线斜率，得到公法线的方程为y-y1=-1/f'(x1)(x-x1)。

7.我们可以将公法线方程与曲线方程联立，解这个方程组来找到公法线与曲线的交点。

8.解这个方程组可能是一个复杂的过程，因此我们可以借助数值计算软件或图形计算器来求解。

9.一旦我们找到了公法线与曲线的交点，我们可以使用勾股定理来计算公法线的长度。

公法线的长度即为从曲线上的其中一点到该交点的直线段长度。

10.将勾股定理应用于公法线交点与曲线上的其中一点，根据坐标计算两点之间的距离。

这样，我们可以通过上述步骤确定公法线的具体长度。

然而，需要注意的是，公法线的长度可能在不同的点处不同。

因此，在计算公法线长度时，我们需要确定特定的点和曲线方程，并根据具体的数值来计算。

跨公法线长度计算公式公法线长度是指从一个点到直线的垂直距离。

在几何学中，我们常常需要计算两个点之间的距离，而其中一点到直线的距离就是公法线长度。

公法线长度的计算可以通过以下公式进行：L = |Ax + By + C| / sqrt(A^2 + B^2)其中，L表示公法线长度，(x, y)表示点的坐标，A、B、C分别是直线的系数。

我们需要明确直线的方程形式。

一般来说，直线可以用一般式方程表示为Ax + By + C = 0。

在此方程中，A、B、C分别表示直线的系数。

对于给定的点P(x, y)和直线Ax + By + C = 0，我们可以使用公式来计算点P到直线的公法线长度。

下面，我们通过一个具体的例子来解释如何应用这个公式。

假设我们需要计算点P(2, 3)到直线2x + 3y - 6 = 0的公法线长度。

我们根据直线的方程，得到直线的系数A = 2，B = 3，C = -6。

接下来，我们将这些值代入公式中：L = |2*2 + 3*3 - 6| / sqrt(2^2 + 3^2)= |4 + 9 - 6| / sqrt(4 + 9)= |7| / sqrt(13)= 7 / sqrt(13)因此，点P(2, 3)到直线2x + 3y - 6 = 0的公法线长度为7 / sqrt(13)。

通过这个例子，我们可以看到如何使用跨公法线长度计算公式来计算点到直线的距离。

这个公式可以在解决几何问题中起到重要的作用。

除了计算点到直线的距离，公法线长度的计算公式还可以应用于其他几何问题。

例如，我们可以使用这个公式来计算两条直线之间的距离。

只需将其中一条直线的方程代入公式中，即可得到两条直线之间的公法线长度。

跨公法线长度计算公式是一种在几何学中常用的计算方法。

通过这个公式，我们可以准确地计算点到直线的距离，并解决各种与几何相关的问题。

在实际应用中，我们可以根据具体情况灵活运用这个公式，以求得准确的结果。