下载文档原格式
全国周培源大学生力学竞赛考试范围（参考）Ⅰ.理论力学(一)静力学(1)掌握力、力矩和力系的基本概念及其性质。
能熟练地计算力的投影、力对点的矩和力对轴的矩。
(2)掌握力偶、力偶矩和力偶系的基本概念及其性质。
能熟练地计算力偶矩及其投影。
(3)掌握力系的主矢和主矩的基本概念及其性质。
掌握汇交力系、平行力系与一般力系的简化方法、熟悉简化结果。
能熟练地计算各类力系的主矢和主矩。
掌握重心的概念及其位置计算的方法。
(4)掌握约束的概念及各种常见理想约束力的性质。
能熟练地画出单个刚体及刚体系受力图。
(5)掌握各种力系的平衡条件和平衡方程。
能熟练地求解单个刚体和简单刚体系的平衡问题。
(6)掌握滑动摩擦力和摩擦角的概念。
会求解考虑滑动摩擦时单个刚体和简单平面刚体系的平衡问题。
(二)运动学(1)掌握描述点运动的矢量法、直角坐标法和自然坐标法，会求点的运动轨迹，并能熟练地求解点的速度和加速度。
(2)掌握刚体平移和定轴转动的概念及其运动特征、定轴转动刚体上各点速度和加速度的矢量表示法。
能熟练求解定轴转动刚体的角速度、角加速度以及刚体上各点的速度和加速度。
(3)掌握点的复合运动的基本概念，掌握并能应用点的速度合成定理和加速度合成定理。
(4)掌握刚体平面运动的概念及其描述，掌握平面运动刚体速度瞬心的概念。
能熟练求解平面运动刚体的角速度与角加速度以及刚体上各点的速度和加速度。
(三)动力学(1)掌握建立质点的运动微分方程的方法。
了解两类动力学基本问题的求解方法。
(2)掌握刚体转动惯量的计算。
了解刚体惯性积和惯性主轴的概念。
(3)能熟练计算质点系与刚体的动量、动量矩和动能；并能熟练计算力的冲量（矩），力的功和势能。
(4)掌握动力学普遍定理(包括动量定理、质心运动定理、对固定点和质心的动量矩定理、动能定理)及相应的守恒定理，并会综合应用。
(5)掌握建立刚体平面运动动力学方程的方法。
了解其两类动力学基本问题的求解方法。
(6)掌握达朗贝尔惯性力的概念，掌握平面运动刚体达朗贝尔惯性力系的简化。
一力学竞赛简介在各门科学中，力学和数学是最为基础和影响范围最广的两门学科，也是关系最为密切的两门学科。
简练的说数理化天地生可统一归纳为物理科学，形象的说，物理科学是一根梁，力学和数学就是两根支柱。
1988年第一届全国青年力学竞赛，每四年举行一次，后来受到周培源基金会的支持，改名周培源大学生力学竞赛，1996年第三届全国周培源大学生力学竞赛，2007年开始每两年举行一次。
力学竞赛宗旨：推动作为基础课的力学教学，增加学生对力学学科的兴趣，活跃教学与学习氛围，发现人才，吸引全社会对力学学科的关注与投入。
竞赛题目特点，总体新颖有趣，难度适中，简明又富于启发性，特别从实践中提炼出来的赛题是亮点。
竞赛题目围绕理论力学和材料力学两门课程进行。
材料力学以理论力学知识为基础，两门课程密切相关。
理论力学主要研究刚体，材料力学研究变形体，两门课程在力学模型和分析方法方面都有所不同。
应仔细研究和了解两门课程在理论模型和方法方面的联系与区别。
力学建模是不可或缺的基本能力之一，也是材料力学教学中相对薄弱的环节。
力学建模要求对实际问题的力学机制有深刻理解，要求有把握全局的定性分析能力。
从不同的角度切入，同一工程问题的力学模型可能具有多样性，对关键因素的提炼有不同见解，造成结果有所差别，只是精度之差，而非正确与错误之别。
二近几届力学竞赛题目分析从2007年开始每两年举行一届全国周培源大学生力学竞赛，出题学校是清华大学，个人卷满分120分，时间三小时，试题总共四题，每道题设置三个问题，内容包括理论力学和材料力学，两个科目的内容和分数基本上各占一半。
不乏理论力学和材料力学的混合问题。
本次试题的风格是趣味性，灵活性和发散性，特点是，把学生所熟悉的力学问题改写成未经加工提炼的状态，这样学生看到的是“问题”或“现象”，而不再是熟悉的“习题”了。
所以特别考察学生的基础知识是否扎实，解题技巧是否灵活，观察能力是否敏锐，建模能力，以及面对复杂问题时能否抓住问题的核心，直接洞察问题实质的能力。
第6届周培源全国大学生力学竞赛初赛（样题）时间3小时，满分120分一、奇怪的独木桥（25分）一位游客在某处发现有座独木桥，上面写着：禁止独自一人过桥。
他发现当地居民的确都是成双结队并且好像以某种相互配合的方式过桥。
他觉得很奇怪，为什么2个人可以过桥而1个人却不能。
等周围没有其它人时他想独自试试，结果没走到半程，就把独木桥压断了而掉入水中。
根据事后他的调查，小河宽4米，独木桥长6米，如图1所示横跨在小河上（支撑点可以认为是铰链约束）。
独木桥采用当地的轻质木材做成，等截面，允许最大弯矩为[]600N mM=⋅。
为方便假设每人的体重均为800N，而独木桥的重量不计。
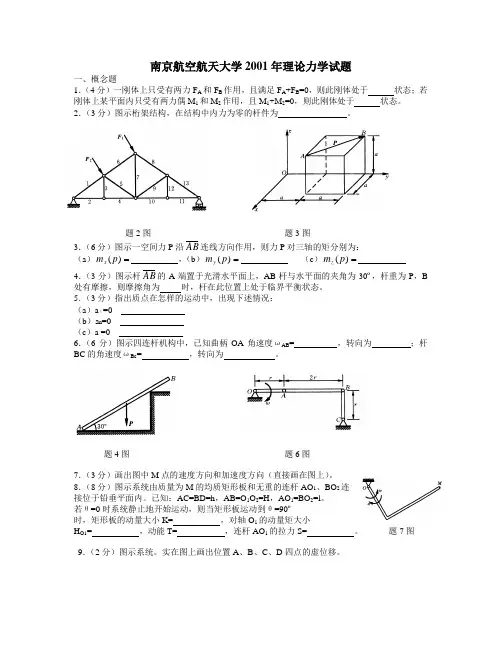
请你分析一下：（1）本问题与力学中的什么内容有关系？（2）如果一个人想过桥，最多能走多远？（3）当地居民过桥时两人需要进行配合，你认为两人应如何配合才能安全过桥？图1 奇怪的独木桥二、模特儿与新型舞台（35分）2a a 有位模特儿在一种新型舞台上练习走台步。
该舞台类似长方形桌子，长为，宽为，有6条等长的桌腿（图2）。
每条桌腿都与水平地面有接触开关，如果接触处有压力就会使对应的一盏灯亮起来。
该模特儿发现，站到舞台不同的位置会有不同数目的灯亮起来，如图2，她站在舞台右上角附近时，左下角的灯就不亮。
如果把模特儿的重量认为是集中载荷，把舞台认为是刚体且不计质量，则（1）本问题与力学中的什么内容有关系？（2）如果模特儿站在舞台的正中央，会有几盏灯亮起来？（3）模特儿在不同区域时会有不同数目的灯亮起来，请在长方形舞台上确定各区域的边界并画出示意图，然后在该区域内写上亮灯的数目（提示，亮灯的数目有可能为6、5、4、3、2、1）。
aa a a图2 模特儿的新舞台 三、魔术师的表演（25分） 魔术师要表演一个节目。
其中一个道具是边长为的不透明立方体箱子，质量为a 1M；另一个道具是长为L 的均质刚性板AB ，质量为2M ，可绕光滑的A 铰转动；最后一个道具是半径为R 的刚性球，质量为3M ，放在刚性的水平面上。
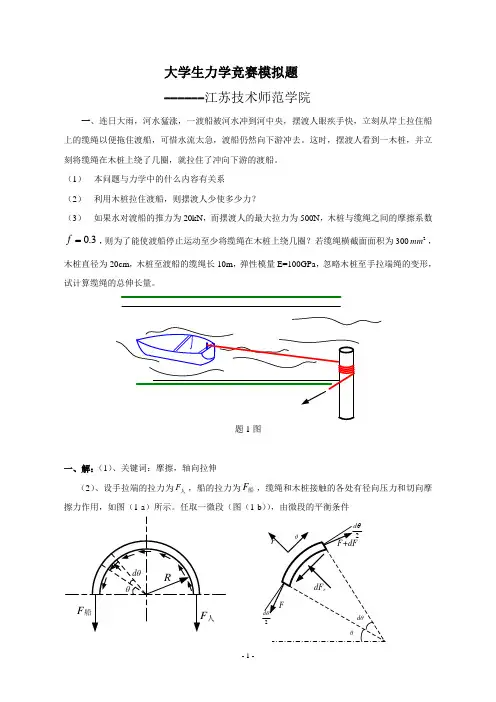
大学生力学竞赛模拟题 ------江苏技术师范学院一、连日大雨，河水猛涨，一渡船被河水冲到河中央，摆渡人眼疾手快，立刻从岸上拉住船上的缆绳以便拖住渡船，可惜水流太急，渡船仍然向下游冲去。
这时，摆渡人看到一木桩，并立刻将缆绳在木桩上绕了几圈，就拉住了冲向下游的渡船。
（1） 本问题与力学中的什么内容有关系 （2） 利用木桩拉住渡船，则摆渡人少使多少力？（3） 如果水对渡船的推力为20kN ，而摆渡人的最大拉力为500N ，木桩与缆绳之间的摩擦系数3.0=f ，则为了能使渡船停止运动至少将缆绳在木桩上绕几圈？若缆绳横截面面积为3002mm ，木桩直径为20cm ，木桩至渡船的缆绳长10m ，弹性模量E=100GPa ，忽略木桩至手拉端绳的变形，试计算缆绳的总伸长量。
题1图一、解：（1）、关键词：摩擦，轴向拉伸（2）、设手拉端的拉力为人F ，船的拉力为船F ，缆绳和木桩接触的各处有径向压力和切向摩擦力作用，如图（1-a ）所示。
任取一微段（图（1-b ）），由微段的平衡条件（1-a ） （1-b ）0=∑r F 02sin 2sin )(=-+-θθd F d dF F dF r （1） 0=∑θF ()02cos 2cos=--+r fdF d F d dF F θθ （2） 对于微小角度θd ，可令 22sinθθd d ≈，12cos ≈θd ，并略去高阶微量2θd dF ⨯，即得fF d dF=θ（3） 分离变量，积分得θf Ae F = （4）其中积分常数由缆绳两端的边界条件确定，有0=θ， 船F F =； 船F A =所以，绕在木桩上缆绳任一截面的拉力为θf e F F 船= （5）所以θf e F F =船人，其中θ为缆绳绕过木桩的角度。
（3）、将N F 500=人，kN F 20=船，f = 0.3代入式（5），得θ3.031020500e ⨯=解得 3.12≈θ rad 所以至少将缆绳绕两圈。
周培源全国大学生力学竞赛模拟题（徐州工程学院）一 某杂技团作飞车走壁表演，设车由A 点开始沿路径AEDBCE 运动，路径的DBC 段为一圆的缺口，而α==<<BOD BOC ，不计摩擦。
（25分）（1）小车在DBC 段运动时与力学中的哪些知识相关？ （2）问高度h 应为多少才能使小车越过缺口循上述路径运动？ （3）又如欲使h 值为最小，则α角应为若干？题一图二 长为l 的钢尺，用两手食指在两端水平托起，当两手食指慢慢平行靠近时，钢尺首先只在一只手上滑动，当滑动一定长度后，又换为只在另一只手上滑动。
（35分）（1）用力学知识简要解释这一现象。
（2）钢尺沿长度方向自重的荷载集度为q ，钢尺与手之间的静摩擦因数为s f ，动摩擦因数为f ，求钢尺在首先滑动的手上能滑动的最大距离d 。
（3）钢尺的材料弹性模量为E ，横截面对中性轴的惯性矩为z I ，求当钢尺在首先滑动的手上滑动最大距离d 时，钢尺两端的转角。
三 人们常可见到这样的杂技表演：一人躺在地上，身上压着一块石板，另一人挥铁锤击石板，石板破了而其底下的人却安然无恙。
（25分）(1)请指出这一表演中所包含的力学概念（或力学问题）。
(2)如果铁锤的质量为1m ，击石头时的速度为1v ，石头的质量为2m ，两者间的恢复因数为k ，碰撞的能量损失为多少？(3)如果铁锤与石板的恢复系数.k=0.5,铁锤1m =5kg ， 2m ＝75kg ，被表演者吸收转变为身体的变形能的能量为多少？四 一条长为2m 的黄铜管，外径D ＝150mm ，壁厚δ＝5mm ，两端封闭，用直径d ＝2.5mm 的钢丝绕在上面，如图1所示（已知钢的弹性模量s E ＝200GPa ，泊松比s μ＝0.25，黄铜的弹性模量c E ＝200GPa ，泊松比c μ＝0.34）。
（35分）题四 图1（1）计算该钢丝中产生的最大应力如下：MPa 7.32785.21505.210200223maxmax max max =+⨯⨯=+=+====d D Ed d D dEEy I y EI I My z z z ρρσ如果钢丝的屈服极限为235Mpa ，上述算式是否正确，为什么？（2）如果在力F ＝400N 作用下用钢丝将管紧密地缠绕一层，计算该钢丝中产生的最大应力，求铜管的应力。
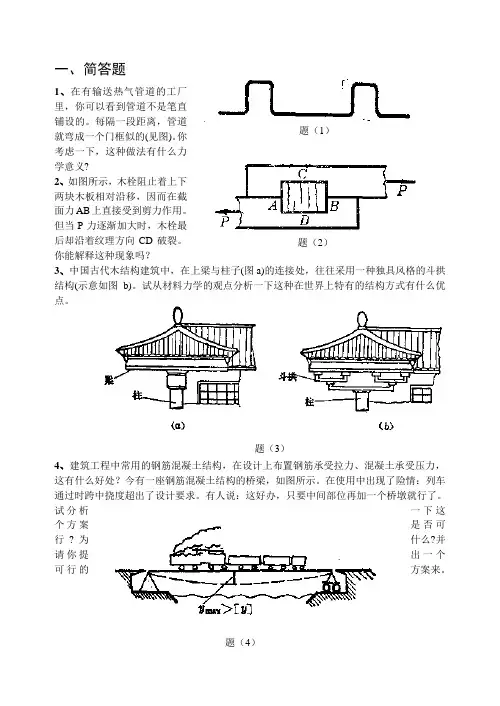
题（3） 一、简答题1、在有输送热气管道的工厂里，你可以看到管道不是笔直铺设的。
每隔一段距离，管道就弯成一个门框似的(见图)。
你考虑一下，这种做法有什么力学意义?2、如图所示，木栓阻止着上下两块木板相对沿移，因而在截面力AB 上直接受到剪力作用。
但当P 力逐渐加大时，木栓最后却沿着纹理方向CD 破裂。
你能解释这种现象吗？3、中国古代木结构建筑中，在上梁与柱子(图a)的连接处，往往采用一种独具风格的斗拱结构(示意如图b)。
试从材料力学的观点分析一下这种在世界上特有的结构方式有什么优点。
4、建筑工程中常用的钢筋混凝土结构，在设计上布置钢筋承受拉力、混凝土承受压力，这有什么好处？今有一座钢筋混凝土结构的桥梁，如图所示。
在使用中出现了险情：列车通过时跨中挠度超出了设计要求。
有人说：这好办，只要中间部位再加一个桥墩就行了。
试分析一下这个方案是否可行?为什么?并请你提出一个可行的方案来。
题（1）题（2）题（4）5、有人作过计算，钢制潜艇在安全的极限潜水深度下，它的浮力要减小3％左右。
这是什么缘故?从材料力学的角度来说，在潜艇的设计中，除了强度和稳定性问题外，还有什么重要问题需要考虑？6、如果你开始学习空手道(气功)，有一件事看来是有趣的。
用赤手空拳作一次击断木板的表演，这牵涉到肌肉强度、打击速度、木材强度以及技术的水平和观众的注意、……等等许多问题。
从材料力学的观点，有一个问题似乎是基本的。
应该对单块木板还是对一叠木板(两者总厚相同，见图)作练功表演呢? 当然，所比较的这两种方案中除单块与层叠这点不同之外，其他条件完全相同。
此外，假定观众离你只有3m ，因而不易受骗，所以你在采用某种巧妙的方案时，还要注意不致露出破绽。
二、计算题7、公元前221—205年，古埃及一个君主下令首席工程师Belisatius 设计一艘特大的战舰。
舰长128m ，宽18．3m ，一个桨就要40个人来划。
显然，在当时这只是一种幻想。
