第6章 互感电路图文

第6章 互感电路
第6章 互感电路
6.1 互感与互感电压 6.2 同名端及其判定 6.3 具有互感电路的计算 *6.4 空芯变压器 本章小结 习题
第6章 互感电路
6.1 互感与互感电压
6.1.1 图6.1中，设两个线圈的匝数分别为N1、N2。在线
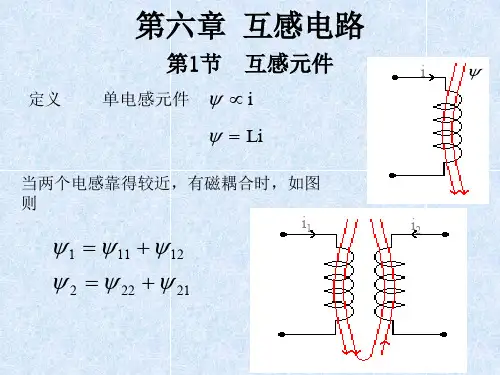
圈1中通以交变电流i1, 使线圈1具有的磁通Φ11叫自感磁 通, Ψ11=N1Φ11叫线圈1的自感磁链。由于线圈2处在i1所 产生的磁场之中, Φ11的一部分穿过线圈2, 线圈2具有的 磁通Φ21叫做互感磁通, Ψ21=N2Φ21叫做互感磁链。这种 由于一个线圈电流的磁场使另一个线圈具有的磁通、 磁链分别叫做互感磁通、 互感磁链。
i2
N2 22
i2
M12
12
i2
N1 12
i2
, M 21
11
i1
N2 21
i1
k M 12M 21 12 21 12 21
L1L2
11 22
1122
而Φ21≤Φ11, Φ12≤Φ22, 所以有0≤k≤1, 0≤M≤
。
L1L2
第6章 互感电路
6.1.4 互感电压
互感电压与互感磁链的关系也遵循电磁感应定律。 与讨论自感现象相似, 选择互感电压与互感磁链两者的 参考方向符合右手螺旋法则时, 因线圈1中电流i1的变化 在线圈2中产生的互感电压为
第6章 互感电路
6.2.2 同名端的测定 如果已知磁耦合线圈的绕向及相对位置, 同名端便很
容易利用其概念进行判定。但是, 实际的磁耦合线圈的绕 向一般是无法确定的, 因而同名端就很难判别。在生产实 际中, 经常用实验的方法来进行同名端的判断。
测定同名端比较常用的一种方法为直流法, 其接线方 式如图6.4所示。当开关S接通瞬间, 线圈1的电流i1经图示 方向流入且增加, 若此时直流电压表指针正偏（不必读取 指示值）, 则电压表“+”柱所接线圈端钮和另一线圈接电 源正极的端钮为同名端。反之, 电压表指针反偏, 则电压 表“-”柱所接线圈端钮与另一线圈接电源正极的端钮为 同名端。
线圈2对线圈1的互感为
M 12
12
i2
可以证明, M12=M21（本书不作证明）, 今后讨论时无须 区分M12和M21。两线圈间的互感系数用M表示, 即
M=M12=M21 互感M的SI单位是亨（H）。
线圈间的互感M不仅与两线圈的匝数、 形状及尺寸有 关, 还和线圈间的相对位置及磁介质有关。当用铁磁材料作 为介质时, M将不是常数。本章只讨论M为常数的情况。
第6章 互感电路
6.2 同名端及其判定
6.2.1 用同名端来反映磁耦合线圈的相对绕向, 从而在分析互
感电压时不需要考虑线圈的实际绕向及相对位置。 当两个线圈的电流分别从端钮1和端钮2流进时, 每个线
圈的自感磁通和互感磁通的方向一致, 就认为磁通相助, 则 端钮1、 2就称为同名端。如图6.1中的两个线圈, i1、i2分别 从端钮a、 c流入, 线圈1的自感磁通Φ11和互感磁通Φ12方向 一致, 线圈2的自感磁通Φ22和互感磁通Φ21方向一致, 则线圈 1的端钮a和线圈2的端钮c为同名端。显然, 端钮b和端钮d也 是同名端。而a、 d及b、 c端钮则称异名端。
u21
d 21
dt
M
di 1 dt
(6.3)
第6章 互感电路
同样， 因线圈2中电流i2的变化在线圈1中产生的互
感电压为
u12
d 21
dt
M
di2 dt
(6.4)
由式（6.3）和式（6.4）可看出, 互感电压的大小 取决于电流的变化率。当di/dt>0 时, 互感电压为正值, 表示互感电压的实际方向与参考方向一致； 当 di/dt <0 时, 互感电压为负值, 表明互感电压的实际方向与参考 方向相反。
第6章 互感电路 图6.2 互感电压与线圈绕向的关系
第6章 互感电路 图6.3 有耦合电感的电路模型
第6章 互感电路
同名端用相同的符号“*”或“Δ”标记。为了便于 区别, 仅将两个线圈的一对同名端用标记标出, 另一对 同名端不需标注。
在电路理论中, 把有互感的一对电感元件称为耦合 电感元件, 简称耦合电感。图6.3所示为耦合电感的电路 模型, 其中两线圈的互感为M, 自感分别为L1、L2。图中 “*”号表示它们的同名端。
第6章 互感电路
当线圈中通过的电流为正弦交流电时, 如
i1=I1msinωt,
i2=I2msinωt
则
u21
M
d1 dt
M
d(I1m sin t)
dt
MI
1m
cos t
MI
1m
sin(t
2
)
第6章 互感电路
同理
u12
MI
2
ms
in(t
2
)
互感电压可用相量表示，即
U 21 jMI1 jX M I1,U12 jMI2 jX M I2
第6章 互感电路 图 6.1 互感应现象
第6章 互感电路
由于i1的变化引起Ψ21的变化, 从而在线圈2中产生 的电压叫互感电压。同理, 线圈2中电流i2的变化, 也会 在线圈1中产生互感电压。这种由一个线圈的交变电流 在另一个线圈中产生感应电压的现象叫做互感现象。
为明确起见, 磁通、磁链、感应电压等应用双下标 表示。第一个下标代表该量所在线圈的编号, 第二个下 标代表产生该量的原因所在线圈的编号。例如，Ψ21表 示由线圈1产生的穿过线圈2的磁链。
第6章 互感电路
6.1.3
两个耦合线圈的电流所产生的磁通, 一般情况下, 只有部分相交链。两耦合线圈相交链的磁通越多, 说 明两个线圈耦合越紧密。耦合系数k用来表示磁耦合线 圈的耦合程度。
耦合系数定义为
k M
(6.2)
L1L 2
第6章 互感电路
因为 所以
L1
11
i1
N1 11
i1
, L1
22
式中，XM=ωM称为互感抗, 单位为欧姆（Ω）。
第6章 互感电路
思考题
1. 互感应现象与自感应现象有什么异同？
2. 互感系数与线圈的哪些因素有关？
3. 已知两耦合线圈的L1=0.04 H, L2=0.06 H, k=0.4, 试求其互感。
4. U 21 jmI1中互感电压的参考方向与互感磁通及
电流的参考方向之间有什么关系？
第6章 互感电路
6.1.2
在非铁磁性的介质中, 电流产生的磁通与电流成正 比, 当匝数一定时, 磁链也与电流大小成正比。选择电 流的参考方向与它产生的磁通的参考方向满足右手螺
旋法则时,
Ψ21∝i1 设比例系数为M21, 则
Ψ21 =M21i1
或
M 12
21
i1
M21叫做线圈1对线圈2的互感系数,