当前位置：文档之家 › 第3章 布尔代数与逻辑函数化简

第3章 布尔代数与逻辑函数化简

  • 格式：ppt
  • 大小：2.01 MB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

第三章布尔代数与逻辑函数化简

第三章布尔代数与逻辑函数化简
F = A B C + BC( A + A) + A C ( B + B) = A B C + ABC + A BC + AB C + A B C
_ _ _ _ _ _ _ _ _ _ _ _ _
和 ( A + A)
_
乘第二项和第三项， ( B + B)
_
(2) 真值表法。将原逻辑函数A、B、C 取不同 值组合起来，得其真值表，而该逻辑函数是将F=1 那些输入变量相或而成的，如表3 - 3所示。
_ _ _ _
_
_
_ _
= A B + A B + ( A B + A B )CD
令 A B + A B = G, 则
F = G + G CD = G + CD = A B + A B + CD
_ _ _
_ _
_
_
_
_
3. 应用多余项定律 ( AB + A C + BC = AB + A C )
例 10 解 化简
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
此例就是用 (C + C ) 和 ( A + A) 分别去乘第三项和第四项， 然后再进行化简。
_
_
6. 添项法
在函数中加入零项因子 x . x 或 x . x f ( AB . ..) ，利用 加进的新项，进一步化简函数。 例 14 化简 = AB C + ABC AB 。 F
第三章 布尔代数与逻辑函数化简
3.1 3.2 3.3 基本公式和规则 逻辑函数的代数法化简 卡诺图化简

布尔代数与逻辑函数化简

布尔代数与逻辑函数化简
根据对偶法则，原式F成立，则其对偶式也一 定成立。
在求对偶式时，为保持原式的逻辑优先关系， 应正确使用括号。
3.1.2 基本法则
公式名称
公式
1、0-1律 2、自等律 3、等幂律 4、互补律 5、交换律 6、结合律 7、分配律 8、吸收律1
A•0 0 A•1 A A• A A A• A 0 A•B B• A A • (B • C) (A • B) • C A(B C) AB AC (A B)(A B) A
F AB AC
A&
B
A&
C
1
F
3.1.3 基本公式的应用
（1）与非-与非式
F AB AC
将与或式两次取反，利用摩根定律一次即可。
F F AB AC AB• AC
A&
B
A&
C
&
F
3.1.3 基本公式的应用
（2）与或非式
F AB AC
① 求出反函数，化简为与或式
② 对反函数取反，即得与或非表达式
F AB AC AB AC
F AB AC
A & 1
B
F
A
C
3.1.3 基本公式的应用
（3）或与式 将与或非式用摩根定律展开，即得或与表达式
F AB AC
AB • AC ( A B)( A C)
A 1 B
A 1 C
&
F
3.1.3 基本公式的应用
（4）或非-或非式 将或与式两次取反，并用摩根定律展开一次即 得或非-或非表达式。
推广：在两项组成的与或表达式中，如果其中一项中含 有原变量 X，而另一项含有反变量 X ，将这两项的其余 因子各自取反，就可得到该函数的反函数。

数字逻辑电路 第三章 布尔代数与逻辑函数化简(52P)

数字逻辑电路 第三章 布尔代数与逻辑函数化简(52P)

例4 F=AD+AD+AB+AC+BD+ACEG+BEG+DEGH 解: 原式=A+AB+AC+BD+ACEG+BEG+DEGH （吸收律1）
=A+AC+BD+BEG+DEGH (吸收律2)
=A+C+BD+BEG+DEGH（吸收律3） =A+C+BD+BEG （多余项定律）
例5
F=AB+BC+BC+AB F=AB+BC+BC（A+A）+AB（C+C） （互补律A+A=1） =AB+BC+ABC+ABC+ABC+ABC （分配律） =AB+BC+ABC+ABC+ABC（吸收律2： AB+ABC=AB） =AB+BC+ABC+ABC （吸收律2： BC+ABC=BC） =AB+BC+AC（吸收律1:ABC+ABC=AC）
反函数
③ 反演法则
例：求F A B C D E的反函数F
F A B C D E A B C D E A BC D E A BC DE
上述过程要反复应用求反律。而利用反演法则直接写出结果。
F A B C D E
3.1.3 基本公式应用
5.交换律
6.结合律 7.分配律 8.吸收律1
A· B= B· A
A· (B· C)= (A· B)· C A(B+C)=AB+AC (A+B)(A+B)=A

数字电子技术教学大纲(物联网工程专业)

数字电子技术教学大纲(物联网工程专业)

《数字电子技术》课程教学大纲课程名称：数字电子技术英文名称：Digital Electronic Technology 课程代码: 课程类别: 必修专业基础学分: 2 学时: 32开课单位: 计算机科学与信息工程学院适用专业: 物联网工程制订人：谭晓东审核人：黄华升审定人: 陶程仁一、课程的性质和目的（一）课程性质本课程是计算机与技术、物联网工程等本科专业的必修专业基础课。

且为主干课程。

本课程主要讲述数字逻辑的基本概念、基本定律和基本分析方法，数字逻辑电路的特性、功能，分析方法及应用。

（二）课程目的课程教学所要达到的目的是：1．能正确理解本课程的基本概念、基本理论；2．掌握数字电路的工作原理、性能和特点；3．掌握数字电路的基本分析方法和设计方法；4．能独立的应用所学的知识去分析和求解从工程中抽象出的逻辑问题以及与专业有关的某些数字电路的实际问题，并具有工程计算和分析能力，为后续专业课程的学习打下基础。

二、与相关课程的联系与分工要求学生具备高等数学、大学物理、电路理论、半导体器件等方面的知识，才能进入该课程的学习，该课程为后续电子计算机及接口技术等方面的课程及专业课程中的电子电路实际应用奠定基础。

三、教学内容及要求第一章数制与代码本章是学习数字逻辑电路及其工作原理的基础，应掌握各种数制、代码的特点及相互之间的转换规律。

1.1 进位计数制1.1.1进位计数制的基本概念1.1.2 常用进位计数制1.2 数制转化1.2.1 非十进制转化成十进制数1.2.2 十进制数转化成其它进制数1.2.3 二进制数转化成八进制数或十六进制数1.2.4 八进制数或十六进制数转化成二进制数1.3 常用代码1.3.1 二—十进制码（BCD码）1.3.2 可靠性编码1.3.3 字符代码【重点与难点】本章主要讲述简单的逻辑运算及常用的逻辑门。

重点是熟练掌握基本逻辑运算、各种门电路的图形符号及其输出函数表达式，正确处理各种门电路使用中的实际问题。

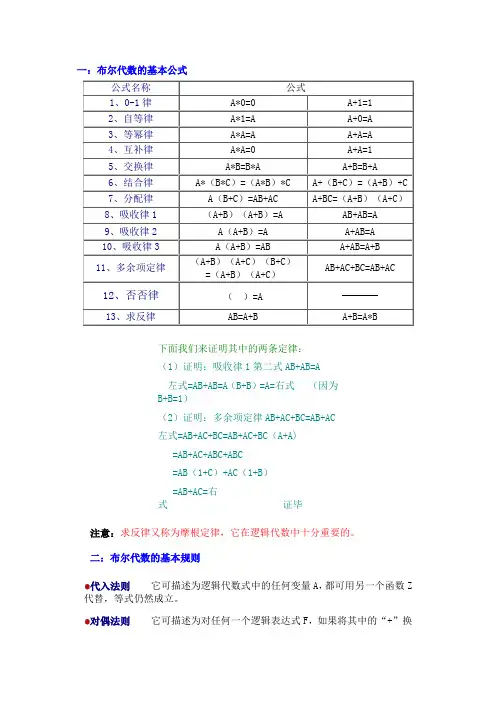
第三章 逻辑函数化简

第三章 逻辑函数化简

一：布尔代数的基本公式公式名称公式1、0-1律A*0=0 A+1=12、自等律A*1=A A+0=A3、等幂律A*A=A A+A=A4、互补律A*A=0 A+A=15、交换律A*B=B*A A+B=B+A6、结合律A*（B*C）=（A*B）*C A+（B+C）=（A+B）+C7、分配律A（B+C）=AB+AC A+BC=（A+B）（A+C）8、吸收律1（A+B）（A+B）=A AB+AB=A9、吸收律2A（A+B）=A A+AB=A10、吸收律3A（A+B）=AB A+AB=A+B11、多余项定律（A+B）（A+C）（B+C）=（A+B）（A+C）AB+AC+BC=AB+AC12、否否律（）=A13、求反律AB=A+B A+B=A*B下面我们来证明其中的两条定律：（1）证明：吸收律1第二式AB+AB=A左式=AB+AB=A（B+B）=A=右式（因为B+B=1）（2）证明：多余项定律AB+AC+BC=AB+AC左式=AB+AC+BC=AB+AC+BC（A+A)=AB+AC+ABC+ABC=AB（1+C）+AC（1+B）=AB+AC=右式证毕注意：求反律又称为摩根定律，它在逻辑代数中十分重要的。

二：布尔代数的基本规则代入法则它可描述为逻辑代数式中的任何变量A，都可用另一个函数Z 代替，等式仍然成立。

对偶法则它可描述为对任何一个逻辑表达式F，如果将其中的“+”换成“*”，“*”换成“+”“1”换成“0”，“0”换成“1”，仍保持原来的逻辑优先级，则可得到原函数F的对偶式G，而且F与G互为对偶式。

我们可以看出基本公式是成对出现的，二都互为对偶式。

反演法则有原函数求反函数就称为反演（利用摩根定律），我们可以把反演法则这样描述：将原函数F中的“*”换成“+”，“+”换成“*”，“0”换成“1”，“1”换成“0”；原变量换成反变量，反变量换成原变量，长非号即两个或两个以上变量的非号不变，就得到原函数的反函数。

逻辑函数公式法化简

逻辑函数公式法化简

逻辑函数公式法化简逻辑函数是分析和设计数字电路的数学依据和基础，用化简后的表达式构成逻辑电路可节省器件，降低成本，提高工作的可靠性，因此将逻辑函数化简为最简式是至关重要的。

逻辑函数的化简一般有两种方法：卡诺图化简法、公式化简法。

本文主要阐述公式化简法的注意事项，其目的在于帮助学生理清解题步骤，减轻学生学习负担。

标签：逻辑函数，公式法，化简1 引言逻辑函数又称布尔代数，是分析和设计数字电路的数学依据和基础，它最初的表达式一般重复性较多，使构成的电路复杂化.用化简后的表达式构成逻辑电路可节省器件，降低成本，提高工作的可靠性，因此将逻辑函数化简为最简式是至关重要的。

而公式化简法是学生学习数字电路中的一个难点，大部分学生在看到题目之后，不知从何处开始下手，不知道用何种方法，即没有解题思路。

2 最简式的判断依据一个与或表达式的最简标准是：1、乘积项个数最少，2、每个乘积项中变量因子最少。

这个标准是一个模糊概念，一个逻辑函数的最简结果应是几个乘积项，乘积项中应是几个变量，显然是不能定论的，鉴别的方法是用基本公式再无法化简时，可认为该逻辑表达式是最简函数。

这就要求逻辑设计者具有一定的逻辑函数化简经验并掌握技巧才行乘积项个数最少。

因此本人通过教学和参考相关教学资料，总结出最简式的判断依据为：1、函数表达式中只存在“与” 、“与-或”逻辑运算（单个自变量可看作它本身与1）；2、与运算乘积项中自变量的个数最少；3、每个自变量在式子中重复出现的机会最少：一般情况下每个自变量以相同的形式出现一次。

以上依据只是定性表达，“最少”的含义只有在具体实例中才能领会，下面就公式法举例说明。

比如：化简函数化简得到：我们来判断此式，勉强符合依据1和2，但A和B以原变量的形式分别出现了两次，不符合依据3中的“最少”条件，因此不是最简式.继续化简如下：3 公式法化简技巧（1）尽量减少记忆的公式由于公式繁多，不易记住，学生即使记住公式，也不知道如何应用公式化简，因此在教学中要尽量减少学生记忆公式，对于能简单计算出的公式，要求学生通过计算或简单化简得到。

第3章 布尔代数与逻辑函数化简

第3章 布尔代数与逻辑函数化简

F = GC + G C = G = A B
布尔代数与逻辑函数化简
例8. F = A B C + AB C 解：令 B C = G ，则
F = A G + AG = A
例9. F = A B C + A B C + A B C + AB C 解：原式 = A C + A C = C 利用等幂律，一项可以重复用几次。 利用等幂律，一项可以重复用几次。
F = AB + AC = A B + A C
布尔代数与逻辑函数化简
2. 逻辑函数不同形式的转换 逻辑函数的形式是多种多样的， 逻辑函数的形式是多种多样的，一个逻辑问题可以用 多种形式的逻辑函数来表示， 多种形式的逻辑函数来表示，每一种函数对应一种逻辑电 路。逻辑函数的表达形式通常可分为五种：与或表达式、 逻辑函数的表达形式通常可分为五种：与或表达式、 与非−与非表达式、与或非表达式、或与表达式、或非 或 与非 与非表达式、与或非表达式、或与表达式、或非−或 与非表达式 非表达式。 非表达式。
布尔代数与逻辑函数化简
例10. F = A B C D + A B C D + A BCD + AB C D + A B C D , 与其余四项均是相邻关系，可以重复使用。 其中 A B C D 与其余四项均是相邻关系，可以重复使用。 解：
ABC D + ABC D = BC D A B C D + AB C D = AC D A B C D + A B CD = A B D ABC D + ABC D = ABC
F = A B + AC
布尔代数与逻辑函数化简

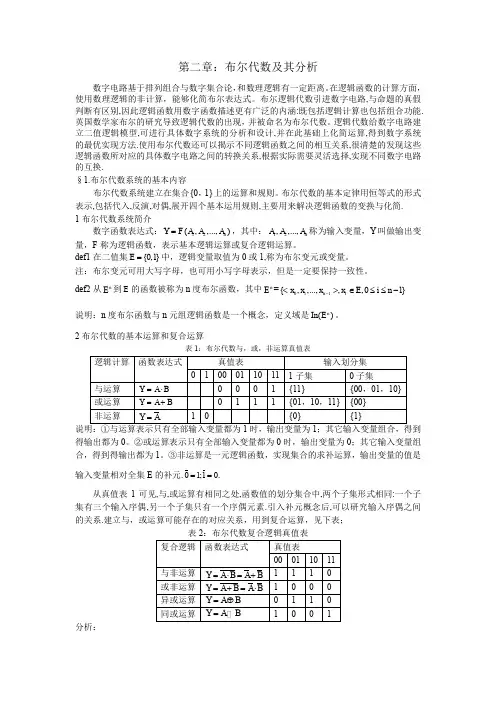
第三章：布尔代数分析与数字电路逻辑化简表示(不同的展开方式)

第三章：布尔代数分析与数字电路逻辑化简表示(不同的展开方式)

第二章：布尔代数及其分析数字电路基于排列组合与数字集合论，和数理逻辑有一定距离。

在逻辑函数的计算方面，使用数理逻辑的非计算，能够化简布尔表达式。

布尔逻辑代数引进数字电路,与命题的真假判断有区别,因此逻辑函数用数字函数描述更有广泛的内涵:既包括逻辑计算也包括组合功能.英国数学家布尔的研究导致逻辑代数的出现，并被命名为布尔代数。

逻辑代数给数字电路建立二值逻辑模型,可进行具体数字系统的分析和设计,并在此基础上化简运算,得到数字系统的最优实现方法.使用布尔代数还可以揭示不同逻辑函数之间的相互关系,很清楚的发现这些逻辑函数所对应的具体数字电路之间的转换关系,根据实际需要灵活选择,实现不同数字电路的互换.§1.布尔代数系统的基本内容布尔代数系统建立在集合{0，1}上的运算和规则。

布尔代数的基本定律用恒等式的形式表示,包括代入,反演,对偶,展开四个基本运用规则,主要用来解决逻辑函数的变换与化简. 1布尔代数系统简介数字函数表达式：12(,,...,)n Y F A A A =，其中：12,,...,n A A A 称为输入变量，Y 叫做输出变量，F 称为逻辑函数，表示基本逻辑运算或复合逻辑运算。

def1在二值集{0,1}E =中，逻辑变量取值为0或1,称为布尔变元或变量。

注：布尔变元可用大写字母，也可用小写字母表示，但是一定要保持一致性。

def2从n E 到E 的函数被称为n 度布尔函数，其中n E =011{,,...,,,01}n i x x x x E i n -<>∈≤≤- 说明：n 度布尔函数与n 元组逻辑函数是一个概念，定义域是()n In E 。

2布尔代数的基本运算和复合运算表1：布尔代数与，或，非运算真值表说明：①与运算表示只有全部输入变量都为1时，输出变量为1；其它输入变量组合，得到得输出都为0。

②或运算表示只有全部输入变量都为0时，输出变量为0；其它输入变量组合，得到得输出都为1。

《数字电子技术(第三版)》3布尔代数与逻辑函数化简

《数字电子技术(第三版)》3布尔代数与逻辑函数化简

《数字电子技术(第三版)》3布尔代数与逻辑函数化简数字电子技术第3章布而代数与逻辑函数化简学习要点：学习要点：三种基本运算，基本公式、定理和规则。

逻辑函数及其表示方法。

逻辑函数的公式化简法与卡诺图化简法。

无关项及其在逻辑函数化简中的应用。

3.1基本公式和规则3.1.1逻辑代数的公式和定理(1)常量之间的关系与运算：00=001=010=011=1或运算：0+0=0非运算：1=00+1=10=11+0=11+1=1(2)基本公式A+0=A0-1律：A1=A互补律：A+A=1A+1=1A0=0AA=0双重否定律：A=A等幂律：A+A=A(3)基本定理AB=BA交换律：A+B=B+A(AB)C=A(BC)结合律：(A+B)+C=A+(B+C)A00A(B+C)=AB+AC1分配律：A+BC=(A+B)(A+C)1BA.BB.A000100000111A.B=A+B反演律(摩根定律):A+B=AB证明分配率：A+BC=(A+B)(A+C)证明：证明：(A+B)(A+C)=AA+AB+AC+BC=A+AB+AC+BC=A(1+B+C)+BC=A+BC分配率A(B+C)=AB+AC等幂率AA=A等幂率AA=A分配率A(B+C)=AB+AC0-1率A+1=1(4)常用公式AB+AB=A还原律：(A+B)(A+B)=AA+AB=A吸收率：A(A+B)=AA(A+B)=ABA+AB=A+B证：A+AB=(A+A)(A+B)明分配率A+BC=(A+B)(A+C)互补率A+A=1互补率A+A=10-1率A·1=11=1 =1(A+B)=A+B冗余律：AB+AC+BC=AB+AC证明：AB+AC+BC=AB+AC+(A+A)BC=AB+AC+ABC+ABC互补率A+A=1互补率A+A=1分配率A(B+C)=AB+AC0-1率A+1=1=AB(1+C)+AC(1+B)3.1.2逻辑代数运算的基本法则(1)代入法则：任何一个含有变量A的等式，如果将所有出现A的位置都用同一个逻辑函数代替，则等式仍然成立。

逻辑函数的化简方法

逻辑函数的化简方法

逻辑函数的化简方法逻辑函数的化简是数理逻辑中的一个重要概念，它指的是将复杂的逻辑函数表示形式简化为更为简洁的形式。

逻辑函数化简的目的是为了方便逻辑分析、简化逻辑电路的设计和优化等。

在进行逻辑函数的化简时，可以使用多种方法，包括真值表、卡诺图、代数法等。

下面我将介绍一些常用的逻辑函数化简方法。

1. 真值表法：真值表法是一种直观的方法，适用于简单的逻辑函数。

它通过列出逻辑函数的所有可能输入和对应的输出，通过观察输入和输出之间的关系，找出逻辑函数的简化形式。

2. 卡诺图法：卡诺图法是一种图形化的方法，适用于中等规模的逻辑函数。

它将逻辑函数的输入和输出用二进制位表示，并用一个方格来表示逻辑函数的真值。

通过观察方格的分布情况，将含有相同输出的方格组合起来，得到逻辑函数的简化形式。

3. 代数法：代数法是一种基于代数运算的方法，适用于任意规模的逻辑函数。

它利用逻辑函数的布尔代数性质，通过运用逻辑运算规则和化简规则，将逻辑函数逐步化简为最简形式。

逻辑函数的化简过程一般包括以下几个步骤：1. 将逻辑函数的输入和输出用适当的变量表示。

例如，对于一个三输入的逻辑函数，可以用A、B、C来表示输入变量，用F表示输出变量。

2. 根据逻辑函数的真值表或卡诺图，观察输入变量与输出变量之间的关系，找出可能的化简形式。

这一步可以根据特定的方法进行，如真值表中可以用观察方式寻找具有相同输出的输入组合，卡诺图中可以利用方格分布情况找到可以合并的项等。

3. 利用逻辑运算规则和化简规则，将逻辑函数逐步化简。

逻辑运算规则包括与、或、非、异或、与非、或非等运算规则，化简规则包括吸收律、分配律、德摩根定理等。

4. 不断重复第3步，直到无法再进行化简为止。

最终得到逻辑函数的最简形式。

需要注意的是，逻辑函数的化简目标是找到最简形式，而不一定是最简单形式。

最简形式是指逻辑函数无法再进行化简，而最简单形式是指逻辑函数中只包含最少的逻辑门。

总的来说，逻辑函数的化简方法包括真值表法、卡诺图法和代数法等。

第3章 逻辑代数

第3章 逻辑代数
解解：：Y Y ABACBCBBDDAABCBCDD
mmm50 5mm1m7 m72mm8m83mmm994mmm11600mmm111133 m 1mm21155m14 mm((55,,77,,88,,99,,1100,,1133,,1155)) MAMB0 MC0M1DM1M2AM2BM3CM3DM4M4MA6BM6MC11D11MM1A122MBMC1144D ABMCMD((00,,11A,,22B,,33C,,44D,,66,,11A11,B,11C22,,1D144))ABC D ABC D
2 真值表
输入变量 输出 A B C···· Y1 Y2 ···· 输入变量所 输出对应的取值 有可能的取 值
ABC F 000 0 001 0 010 0 011 1 100 0 101 1 110 1 111 1
2. 逻辑函数（表达）式 将逻辑函数中输出变量与输入变量之间的逻辑关系 用与、或、非三种运算符号连接起来的表达式
交换律
7
A·(B·C) = (A·B)·C
16 A+(B+C)=(A+B)+C 结合律
8
A·(B+C)=A·B + A·C 17 A+B·C =(A+B) ·(A+C) 分配律
9
AB A B
18
A B AB
反演律
公式（17）的证明：A+BC=(A+B)(A+C)
证明:
右边 =(A+B)(A+C)
偶式，记作 Y 。
所谓对偶定理是指，若两个逻辑函数式相等，那 么它们的对偶式也相等。
AB AC BC AB AC
( A B)( A C)(B C) ( A B)( A C)

第3章-布尔代数与逻辑函数化简

第3章-布尔代数与逻辑函数化简

与项用与门实现
运算次序为先非后与再或，因此用三级电路实现之。
根据逻辑式画逻辑图的方法:
将各级逻辑运算用 相应逻辑门去实现。
布尔代数与逻辑函数化简
例1 图示为控制楼道照明的开关电路。两 个单刀双掷开关 A 和 B 分别安装在楼上和 楼下。上楼之前，在楼下开灯，上楼后关 灯；反之，下楼之前，在楼上开灯，下楼 后关灯。试画出控制功能与之相同的逻辑 电路。
ACB AC D BD ACB ACD ABC AD CD
布尔代数与逻辑函数化简
消去法 运用吸收律 A AB A B ，消去多余因子。
Y AB AC BC AB ( A B)C AB ABC AB C
Y AB AB ABCD ABCD
布尔代数与逻辑函数化简
但如果将函数化简后其函数式为 F=AC+B
只要两个门就够了， 如图3 - 4所示。
A
&
C
B
≥1 F
图 3 – 4 函数化简后的逻辑 图
布尔代数与逻辑函数化简
三、代数化简法
运用逻辑代数的基本定律和
公式对逻辑式进行化简。
并项法 运用 AB AB A，
将两项合并为一项，并消去一个变量。
0 –1 ·11律= 1
0+A=A
重叠律
互补律
1+A=1 A+A=A
1 ·A = A A ·A = A
0 ·A = 0
还原律
布尔代数与逻辑函数化简
二、基本定律 (一) 与普通代数相似的定律
交换律 A + B = B + A
A ·B = B ·A
结合律 (A + B) + C = A + (B + C) (A ·B) ·C = A ·(B ·C)

第3章布尔代数与逻辑函数化简分解

第3章布尔代数与逻辑函数化简分解

_
________
(e)F A B A C 或非表达式
布尔代数与逻辑函数化简
3.2 逻辑函数的代数法化简
一、逻辑函数及其表示方法
逻辑函数描述了某种逻辑关系。 常采用真值表、逻辑函数式、卡诺图和逻辑图等表示。
1. 真值表
列出输入变量的各种取值组合及其对
应输出逻辑函数值的表格称真值表。
列 (1)按 n 位二进制数递增的方式列
A + AB = A (1 + B) = A
布尔代数与逻辑函数化简
(二) 逻辑代数的特殊定理
吸收律 A + AB = A 推广公式：
摩根定律(又称反演律)
推A广B公式A ·：B A+B A B A+B A ·B
00 1 1
00 1 1
思110 考101：((12011))
若已1知 若已01知
A+ AB
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
输出变量 Y 1 1 1 0 1 1 1 0 1 1 1 0 0 0 0 0
布尔代数与逻辑函数化简
2. 逻辑函数式 表示输出函数和输入变量逻辑关系的 表达式。又称逻辑表达式，简称逻辑式。
真值表 (1)找出函数值为 1 的项。 逻辑(函2)数将式这一些般项根中据输真入值变表量、取卡值诺为图1或的逻用辑原图变写量出代。替，
逻辑式
取值为 0 的用反变量代替，则得到一系列与项。
(3)将这些与项相加即得逻辑式。

逻辑函数的化简

逻辑函数的化简

A BC (A B)(A C)
注意：在运用反演规则和对偶规则时，必须按照逻辑运算 的优先顺序进行：先算括号，接着与运算，然后或运算，最后非 运算，否则容易出错。
逻辑函数的表达式
一个逻辑函数的表达式可以有与或表达式、或与表达式、 与非-与非表达式、或非-或非表达式、与或非表达式5种表示 形式。
（１）利用公式Ａ＋ＡＢ＝Ａ，消去多余的项。
是另项是
Y1 AB ABCD(E F ) AB
多外的另
运用摩根定律 余 一 因 外 如
的个子一果
。乘，个乘
Y2 A B CD ADB A BCD AD B ( A AD) (B BCD) A B
积则乘积 项这积项
（２）利用公式Ａ＋ＡＢ＝Ａ+Ｂ，消去多余的变量。
m4 ABC、m5 ABC、m6 ABC、m7 ABC
最小项的编号： 把与最小项对应的变量取值当成二进制数，与之
相应的十进制数，就是该最小项的编号，用 mi 表示。 对应规律：原变量 1 反变量 0
ABC ABC ABC ABC ABC ABC ABC ABC
000 001 010 011 100 101 110 111
例如： Y AB AC
= AB• AC
与-或 与非-与非
A B•A C AB AC
AB AC AB• AC A B AC
与-或-非 或-与
A BA C A B A C或非-或非
2、最简与-或表达式
所谓最简与-或表达式，是指乘积项的个数是最少 的，而且每个乘积项中变量的个数也是最少的与-或 表达式。这样的表达式逻辑关系更明显，而且便于 用最简的电路加以实现（因为乘积项最少，则所用 的与门最少；而每个乘积项中变量的个数最少，则 每个与门的输入端数也最少），所以化简有其实用 意义。

逻辑代数基本原理及公式化简

逻辑代数基本原理及公式化简

THANKS
感谢观看
未来发展方向与挑战
新技术与新应用
随着技术的不断发展，数字电路设计面临着 新的挑战和机遇，需要不断探索新的设计方 法和工具，以适应新的需求。
复杂系统设计
随着系统规模的扩大和复杂性的增加，需要研究更 加高效的设计方法和算法，以应对复杂系统的设计 挑战。
人工智能与自动化
人工智能和自动化技术的发展为数字电路设 计提供了新的思路和方法，可以进一步提高 设计的效率和智能化水平。
02
利用逻辑代数基本原理，可以分析组合逻辑电路的输入和输出
关系，简化电路结构。
通过公式化简，可以将复杂的逻辑表达式转换为简单的形式，
03
便于理解和应用。
时序逻辑电路的分析与设计
01
02
03
时序逻辑电路由触发器 和逻辑门电路组成，具
有记忆功能。
利用逻辑代数基本原理 ，可以分析时序逻辑电 路的状态转移和输出特
分配律与结合律
分配律
A⋅(B+C)=A⋅B+A⋅C，(A+B)⋅C=A⋅C+B⋅C
结合律
(A+B)+C=A+(B+C)，(A⋅B)⋅C=A⋅(B⋅C)
公式化简的步骤与技巧
利用分配律和结合律化简
利用吸收律和消去律化简
利用吸收律和消去律简化表达式 ，消除冗余项。
利用分配律和结合律将表达式重 组，便于化简。
在自动化控制系统中，逻辑代数用于描述和优化控制逻辑。
逻辑代数的发展历程
起源
逻辑代数由英国数学家乔治·布尔（George Boole ）在19世纪中叶提出。
发展
随着电子技术和计算机科学的进步，逻辑代数在 20世纪得到了广泛的应用和发展。

第3章 布尔代数与逻辑函数化简

第3章 布尔代数与逻辑函数化简

由上面可以看出反复用摩根定律即可，当函数较 复杂时，求反过程就相当麻烦。
逻辑代数与逻辑函数
练习二
反演和对偶法则
1、求下面函数F的反函数F
F = AB+C+AD
2、求下面函数F的对偶式F’
F = A（BC+BC）+AC
3、说明对偶法则和反演法则的区别
逻辑代数与逻辑函数
3.1.3 逻辑函数的表达式的形式与转换方法
_ _ _ _ _ _
_
逻辑代数与逻辑函数
例2（2）法2
F A B C D E
F A B C D E A B C D E A B C D E A B C D E
_ _ _ _ _ _ _ _ _ _
_
_
解：用摩根定律
________
( e) F A B A C 或非表达式
逻辑代数与逻辑函数
3.2
逻辑函数的代数法化简
3.2.1 逻辑函数与逻辑图 从实际问题总结出的逻辑函数可以用门电路组合 成逻辑图。
A B
&
≥1
1
1
F
&
图 2 – 14 AB A B 函数的逻辑图
_ _
逻辑代数与逻辑函数
从逻辑问题概括出来的逻辑函数式， 不一定是最 简式。化简电路，就是为了降低系统的成本，提高电 路的可靠性，以便用最少的门实现它们。例如函数：
_
_ ___Fra bibliotek_例4 求 F AB A C 的反函数 解： F AB AC ( A B) ( A C )
AA AB BC AC AB AC
_
逻辑代数与逻辑函数
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

布尔代数与逻辑函数化简
(二) 逻辑代数的特殊定理
吸收律 A + AB = A
A + AB = A (1 + B) = A
布尔代数与逻辑函数化简
(二) 逻辑代数的特殊定理
吸收律 A + AB = A 推广公式：
摩根定律(又称反演律) 推广公式： A+B A B A· B A B A+B A · B 0 0 1 1 0 0 1 1 0 1 1 1 0 A 0 0 思考：(1) 若已知 A + B = 1 + C，则 B = C 吗？ 1 0 1 1 1 0 0 0 (2) 若已知 AB = AC，则 B = C 吗？ 1 1 0 0 1 1 0 0
逻辑变量与常量的运算公式
0–1律 0+A=A 1+A=1 1· =A A 0· =0 A
重叠律
A+A=A A· =A A
互补律
还原律
布尔代数与逻辑函数化简
二、基本定律
(一) 与普通代数相似的定律
交换律 结合律 分配律 A+B=B+A (A + B) + C = A + (B + C) A (B + C) = AB + AC A· =B· B A (A · · = A · · B) C (B C) A + BC = (A + B) (A + C) 普通代数没有！ 逻辑等式的 证明方法 利用真值表
例如 A 0 0 0 0 1 1 1 1 B 0 0 1 1 0 0 1 1 C 0 1 0 1 0 1 0 1 Y 1 0 0 0 0 0 0 1
逻辑式为
ABC
布尔代数与逻辑函数化简
3. 逻辑图
例如 画
由逻辑符号及相应连线构成的电路图。 的逻辑图 相加项用或门实现
反变量用非门实现
与项用与门实现 运算次序为先非后与再或，因此用三级电路实现之。 根据逻辑式画逻辑图的方法: 将各级逻辑运算用 相应逻辑门去实现。
变换时注意： (1) 不能改变原来的运算顺序。 (2) 反变量换成原变量只对单个变量有效，而长非 号保持不变。
原运算次序为 可见，求逻辑函数的反函数有两种方法： 利用反演规则或摩根定律。
布尔代数与逻辑函数化简
(三) 对偶规则
对任一个逻辑函数式 Y，将“· ”换成 “+”，“+”换成“· ”，“0”换成 “1”，“1”换成“0”，则得到原逻 辑函数式的对偶式 Y 。
_ _ _ _
A B AB A B AB ( A B )( A B)
A A AB A B B B AB A B
_ _ _ _ _ _
布尔代数与逻辑函数化简
2. 逻辑函数不同形式的转换 逻辑函数的形式是多种多样的，一个逻辑问题可以 用多种形式的逻辑函数来表示， 每一种函数对应一种逻
列 真 值 表 方 法
出输入变量的各种取值组合。
(2) 分别求出各种组合对应的输出 逻辑值填入表格。
布尔代数与逻辑函数化简
例如 求函数 Y AB CD 的真值表。
输 A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 B 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 入 变 C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 量 D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 输出变量 Y 1 1 1 0 1 1 1 0 1 1 1 0 0 0 0 0
&
≥1 F
(c)
A B A C
≥1
&
≥1
F
A C
(d)
(e)
图 3 –1 同一逻辑的五种逻辑图
( a ) F AB A C与或表达式; (b) F AB A C与非表达式;
( c ) F A B A C 与或非表达式 ( d ) F ( A B )( A C )或与表达式;
对偶规则：两个函数式相等，则它们的对偶式也相等。 变换时注意：(1) 变量不改变 (2) 不能改变原来的运算顺序 A + AB = A
A · + B) = A (A
应用对偶规则可将基本公式和定律扩展。
布尔代数与逻辑函数化简
四、基本公式应用 1. 证明等式
例 3 用公式证明 A B A B A B AB 解
_
_
_
A B A B 这是两变量的求反公式， 若将等
A B C A B C A B C
__________ __ _ _______ _ _ _
_
_
式两边的B用B+C代入便得到
这样就得到三变量的摩根定律。
布尔代数与逻辑函数化简
(二) 反演规则
对任一个逻辑函数式 Y，将“· ”换成 “+”，“+”换成“· ”，“0”换成“1”， “1”换成“0”，原变量换成反变量，反变量 换成原变量，则得到原逻辑函数的反函数 Y 。
化 使逻辑式最简，以便设计出最简的逻辑电路， 简 从而节省元器件、优化生产工艺、降低成本和提 意 义 高系统可靠性。 不同形式逻辑式有不同的最简式，一般先求取 最简与 - 或式，然后通过变换得到所需最简式。
布尔代数与逻辑函数化简
最简与 - 或式标准
(1)乘积项(即与项)的个数最少 (2)每个乘积项中的变量数最少
4 个输入 变量有 24 = 16 种取 值组合。
布尔代数与逻辑函数化简
2.
逻辑函数式
表示输出函数和输入变量逻辑关系的 表达式。又称逻辑表达式，简称逻辑式。
真值表 (1)找出函数值为 1 的项。 (2)将这些项中输入变量取值为 1 的用原变量代替， 逻辑函数式一般根据真值表、卡诺图或逻辑图写出。 取值为 0 的用反变量代替，则得到一系列与项。 逻辑式 (3)将这些与项相加即得逻辑式。
A B C
A BC
A B C
&
B C
B
图3-3 F原函数的逻辑图
布尔代数与逻辑函数化简
但如果将函数化简后其函数式为 F=AC+B
只要两个门就够了， 如图3 - 4所示。
A C B
&
≥1 F
图 3 – 4 函数化简后的逻辑 图
布尔代数与逻辑函数化简
三、代数化简法
运用逻辑代数的基本定律和 公式对逻辑式进行化简。
利用基本公式和基本定律
布尔代数与逻辑函数化简
例1 证明等式 A + BC = (A + B) (A + C) 解： 真值表法 A B C A + BC (A + B) (A + C) 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 1 1 0 1 1 1 1 1 0 0 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 公式法 右式 = (A + B) (A + C) 用分配律展开 = AA + AC + BA + BC = A + AC + AB + BC = A (1 + C + B) + BC = A · +BC 1 = A + BC = 左式
Y A( BC BC ) A( BC BC ) AB C A( B C ) A
布尔代数与逻辑函数化简
F AB C AB C
解
_
_
令 B C G, 则
_
F A G AG A
_
F A B C A B C A B C AB C
解
F AC AC C
_ _ _ _
_ _ _
_
_
_ _
_
利用等幂律，一项可以重复用几次。
布尔代数与逻辑函数化简
F A B C D A B C D A B CD A B C D A B C D,
_ _ _
_ _ _
_
_ _ _
_ _
_
_
_ _
其中 A B C D与其余四项均是相邻关系，可以重复使用。 解
(2) 与或非式。 首先求出反函数
_
_
F AB A C A B A C
_
_
_
_ _
然后再取反一次即得与或非表达式
F A B AC
_
_ _
布尔代数与逻辑函数化简
(3) 或与式。 将与或非式用摩根定律展开， 即得或与表达式如下：
F A B A C A B A C ( A B )( A C )
(4) 或非-或非式。
将或与表达式两次取反， 用摩根定律展开一次得或非 -或非表达式
_
_ _
_ _ _
_
F ( A B )( A C ) A B A C
_
_
布尔代数与逻辑函数化简
A B A C
&
≥1
A B F A C
& & &
(b) A B ≥1 ≥1 ≥1 F
&
(a)
A B A C
辑电路。 逻辑函数的表达形式通常可分为五种： 与或表
达式、 与非-与非表达式、与或非表达式、或与表达式、 或非-或非表达式。
布尔代数与逻辑函数化简
_
例 4 将函数与或表达式 F AB A C 转换为其它形式。 解 (1) 与非-与非式。 将与或式两次取反，利用摩根定律可得
F AB A C AB A C
用与门个数最少 与门的输入端数最少
最简与非式标准 (1)非号个数最少 (2)每个非号中的变量数最少 用与非门个数最少 与非门的输入端数最少