当前位置：文档之家 › 135-5具有无关项的逻辑函数及其化简(精)

135-5具有无关项的逻辑函数及其化简(精)

  • 格式：ppt
  • 大小：263.00 KB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

具有无关项的逻辑函数及其化简PPT培训课件

具有无关项的逻辑函数及其化简PPT培训课件

04
实例演示与解析
实例一：具有无关项的逻辑函数化简
总结词
通过实例演示，介绍如何对具有无关项的逻辑函数进行化简。
详细描述
首先，介绍具有无关项的逻辑函数的概念，即函数中存在一些与输出无关的项。 接着，通过具体实例演示如何识别这些无关项，并运用逻辑代数的基本定律和规 则，将这些无关项化简掉，得到一个更简洁的逻辑函数表达式。
总结词
适用于任意复杂的逻辑函数，通用性强。
详细描述
公式法化简适用于任意复杂的逻辑函数，不受函数形式 限制，通用性强，是逻辑函数化简中最常用的方法之一 。
总结词
需要熟练掌握逻辑代数的基本公式和定律。
详细描述
公式法化简要求熟练掌握逻辑代数的基本公式和定律， 能够灵活运用进行化简，对于初学者可能需要一定时间 来熟悉和掌握。
具有无关项的逻辑函数及 其化简ppt培训课件
• 引言 • 具有无关项的逻辑函数 • 逻辑函数的化简方法 • 实例演示与解析 • 总结与展望
01
引言
逻辑函数及其化简的定义
逻辑函数
在逻辑电路中，输入和输出之间存在 一定的逻辑关系，这种关系可以用逻 辑函数来表示。逻辑函数通常由逻辑 变量和逻辑运算符组成。
通过具体实例演示了如何运用不同的化简 方法对具有无关项的逻辑函数进行化简。
未来研究方向与挑战
研究方向
探讨了未来在逻辑函数及其化简 领域可能的研究方向，如更高效 的化简算法、多值逻辑函数的化
简等。
挑战与问题
指出了当前研究中存在的一些挑战 和问题，如如何处理大规模逻辑函 数的化简、如何提高化简的精度和 效率等。
05
总结与展望
逻辑函数及其化简的总结
逻辑函数及其化简的基本概念

逻辑函数及其化简

逻辑函数及其化简

上页 下页
2.4 逻辑函数及其表示方法
2.4 .1逻辑函数
逻辑函数的定义 实际的逻辑问题描述
2.4 .2逻辑函数的表示方法
逻辑真值表
逻辑函数式
逻辑图
各种表示方法间的互相转换
2.4 .3逻辑函数的两种标准形式
最小项
最小项表达形式
最大项
最大项表达形式
电子技术基础精品课程——数字电子技术基础
上页 下页
2.4.1 逻辑函数
例如 : L ( A B )( A C)，则其对偶式为 L' AB AC
如恒等式( A B )( A C ) A BC成立, 则其对偶式为AB AC A( B C )也成立。 例如：1 A A,0 A 0成立。 则其对偶式为0 A A,1 A 1也成立。
电子技术基础精品课程——数字电子技术基础
一、(逻辑)真值表 利用表格的形式罗列逻辑函数输入变量的所有可能取值及输
出变量之间的一一对应的数值关系的一种数值表。
输入
例如：举重裁判电路
A
B
C
的真值表
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
输出 Y 0 0 0 0 0 1 ABC 1 ABC 1 ABC
电子技术基础精品课程——数字电子技术基础
上页 下页
二、逻辑函数式 把输出与输入变量的关系写成与，或、非等运算的组合关
系式.
例如： Y AB AC
Y F ( A, B, C)
Y A( B C )
ABC ABC ABC

逻辑函数的卡诺图化简

逻辑函数的卡诺图化简

第5讲 逻辑函数 的卡诺图化简
例1. 化简函数F(A,B,C,D)=∑m(3,4,5,7,9,13,14,15)。 解：首先作出逻辑函数F的卡诺图如下：
Digital Logic Circuit
F ( A, B,C, D) ABC ABC ACD ACD
Digital Logic Circuit
F(A,B,C)=∑m(0,1,5,7)+∑d(4,6)
化简具有任意项的逻辑函数的步骤是：
①画出函数对应的卡诺图，任意项对应的小方格填上φ 或d或×。 ②按2的整数次幂为一组构成卡诺圈，如果任意项方格为1时可以圈得 更大，则将任意项当作1来处理，否则当0处理。未被圈过的任意项一律当 作0处理。
③写出化简的表达式。
可见，函数的化简结果不具有唯一性，函数表示的唯一性仅在最大项 表达式或最小表达式中才具有。
5. 具有任意项的逻辑函数的化简
第5讲 逻辑函数 的卡诺图化简
Digital Logic Circuit
任意项（无关最小项）：不决定函数的值的最小项。
从定义可以看出，与任意项对应的逻辑函数值既可以看成1，也可以看 成0。因此在卡诺图或真值表中，任意项常用φ 或d或×来表示；在函数表 达式中常用φ 或d来表示任意项。如：
④写出最简的函数表达式。
演示1
演示2
基本步骤图示
第5讲 逻辑函数 的卡诺图化简
逻辑表达式 Y(A,B,C,D)=m(3,5,7,8,11,12,13,15) 或真值表
Digital Logic Circuit
1
卡诺图
1
AB
CD
00 01 11
10
00 0
0
1
1

利用无关项化简逻辑函数

利用无关项化简逻辑函数
注意：化简时，需要的d当作“1”； 不需要的d当作“0”。
尽量使用与尽量不用的辩证关系！
2.5.4 具有多个输出的逻辑函数的化简 本小节内容，请同学根据课件及教材，自学！ 不作为教学要求。
对于同一组输入变量，具有多个输出的函数称为多数出函数。 单输出函数的化简目标是：逻辑函数的表达式中项数最少，每项中的 变量数最少。 多输出函数的化简目标是总体最简，即多输出函数的总项数最少，每 项中的变量数最少。其方法是在单个函数化简的基础上，谋求使用多 输出函数的各个函数间的公共项。
请同学自画化简前后电路，比较之。
2. 禁止逻辑法
与项
AC BD
BC AD
CDAB
头因子
A
BC
CD
尾因子 C
BD AD
AB
替代尾因子 C , AC
BD , ABD AD , ACD , ABD , ABCD
AB , ABC , ABD , ABCD
按照共享替代尾因子的选择原则，应选 ABD 和 C
F = AC ABD + BC ABD + CD ABD
2.5.3 利用无关项化简逻辑函数
或称：不（非）完全定义的逻辑函数的化简
前面讨论中，逻辑函数取值和输入变量的 2n 种取值均相关，即： 有m种取值使函数值为1，则有（ 2n - m）种取值使函数值为0。
在某些特殊电路中，其输出并不是与 2n 种输入组合都有关的， 而是仅与其中一部分有关，而另一部分输入组合（无关项）不影响 输出。
例1：已知多数出函数，试用最少数目的与非门实现其电路。
⎧ ⎪ ⎨
F1 = ∑ m 4 ( 2 ,3,4 ,6 ,7 ,9 ,12 ,13 ,14 ,15 ) F2 = ∑ m 4 (0 ,2 ,4 ,6 ,7 ,8 ,12 ,14 ,15 )

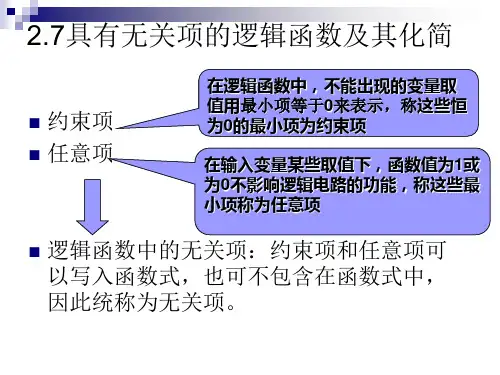
2.7 具有无关项的逻辑函数及其化简

2.7 具有无关项的逻辑函数及其化简

Y B AC
[例] 化简逻辑函数
约束条件
Y AC D ABC D AB C D AB AC 0
CD AB 简与或表达式
01 11 10
1
1
Y C D B D AD AB AC 0
1
注意：合并时，究竟把 ╳ 作为 1 还是作为 0 应以得到 的包围圈最大且个数最少为原则。
111
(2) 约束项：不会出现的变量取值所对应的最小项。
(3) 约束条件： 由约束项相加所构成的值为 0 的 逻辑表达式。
2. 约束条件的表示方法
① 在真值表和卡诺图上用叉号(╳)表示。 ② 在逻辑表达式中，用等于 0 的条件等式表示。 例如，上例中 ABC 的不可能取值为 000 011 101 110 约束项： ABC
例:
Y ( A, B, C , D) m(1,2,5,6,9) 约束条项: m10 m11 m12 m13 m14 0
CD AB 00 01 11 10 1 1 00 1 1 01 11 10 1
Y CD C D
一、 约束的概念和约束条件
1. 约束、约束项、约束条件 (1) 约束： 输入变量取值所受的限制 例如，逻辑变量 A、B、C，分别表示电梯的 升、降、停 命令。 A = 1 表示升，B = 1 表示降，C = 1 表示停。
ABC 的可能取值 001 不可能取值 000
010 011
100 101
110
2.7具有无关项的逻辑函数及其化简
约束项 任意项
在逻辑函数中，不能出现的变量取 值用最小项等于0来表示，称这些恒 为0的最小项为约束项 在输入变量某些取值下，函数值为1 或为0不影响逻辑电路的功能，称这 些最小项称为任意项

第11讲 具有无关项的逻辑函数的化简

第11讲 具有无关项的逻辑函数的化简
CD AB 00 01 11 10
00 × × 1 × 01 × × 0 0 11 1 0 0 1 1100 11 11 11 ××
（3）写出逻辑函数的最简与或表达式。
Y AD11 B
第1章 逻辑代数基础
[例2] 将含有约束项的逻辑函数用卡诺图化简为最简与或式
F(A，B，C，D) m(0，2，4，8，9，14) d(1，6，10，11，12，15)
2
第1章 逻辑代数基础
例1-9 十字路口的交通信号灯，设红、绿、黄分别用A、 B、C来表示；灯亮用1表示，灯灭用0表示；停车时Y=1，通 车时Y=0。写出该问题的逻辑表达式。
解 交通信号灯在实际工作时，一次只允许一个灯亮， 不允许有两个或两个以上的灯同时亮。在灯全灭时，表示此 处交通不受管制，车辆可以自由通行。该逻辑问题可用表 1.8来表示。
第1章 逻辑代数基础
第11讲 具有无关项的逻辑函数的化简
1
第1章 逻辑代数基础
1.6.4 具有无关项的逻辑函数化简 1. 具有无关项的逻辑函数 一般的逻辑函数，对应于每一组变量的取值，都能得到
一个完全确定的函数值(0或1)，如果一个逻辑函数有n个变 量，函数就有2n个最小项，对应于每一个最小项，函数都有 一个确定的值。
第1章 逻辑代数基础 21
解 (1) 列出函数的真值表，如表1.9所示。
14
第1章 逻辑代数基础 15
第1章 逻辑代数基础
由真值表写出函数的逻辑表达式为
也可以根据真值表画出函数的卡诺图，如图1.25(a)所示。 (2) 用图形法化简。合并函数的最小项，得到函数的最
简与或表达式为
(3) 画出函数的逻辑图，如图1.25(b)所示。
6
第1章 逻辑代数基础

逻辑函数的卡诺图法化简

例4 ：用卡诺图表示4变量逻辑函数：F = ABC + CD + BD
数字电路与逻辑设计
解: 直接填入
CD 00
01
00 01 11 10
0
10
0
1
11
0
11 0
11
1
10 0
00
0
电子工 程学院
School of Electronic Engineering
厚夜博学
第二章逻辑函数及其简化
例5:用卡诺图表示4变量逻辑函 数:
School of Electronic Engineering
厚饱博学
第二章逻辑函数及其简化
数字电路与逻辑设计
(2)如不是最小项表达式，应先将其先化成最小项表达式，再填入卡诺图。
例3 ：用卡诺图表示4变量逻辑函数：F = ABC + ABD +
AC 解：F = ABC+ABD+AC
=ABCD + ABCD + ABCD + ABCD +
F B 00 01 11 10
C 0
Jq
0
0
0
0
0
0
1
F
IF = AC
B 00 01
11
10
C
0
0
0
0
0
0
0
1
F
B 00 01 11 10
C
0A 0
0
0
0
0
0
1
IF = BC
\ F = AB
电子工 程学院
School of Electronic Engineering
厚饱博学

(完整版)逻辑函数的卡诺图化简法

第十章 数字逻辑基础补充：逻辑函数的卡诺图化简法1．图形图象法：用卡诺图化简逻辑函数，求最简与或表达式的方法。

卡诺图是按一定规则画出来的方框图。

优点：有比较明确的步骤可以遵循，结果是否最简，判断起来比较容易。

缺点：当变量超过六个以上，就没有什么实用价值了。

公式化简法优点：变量个数不受限制缺点：结果是否最简有时不易判断。

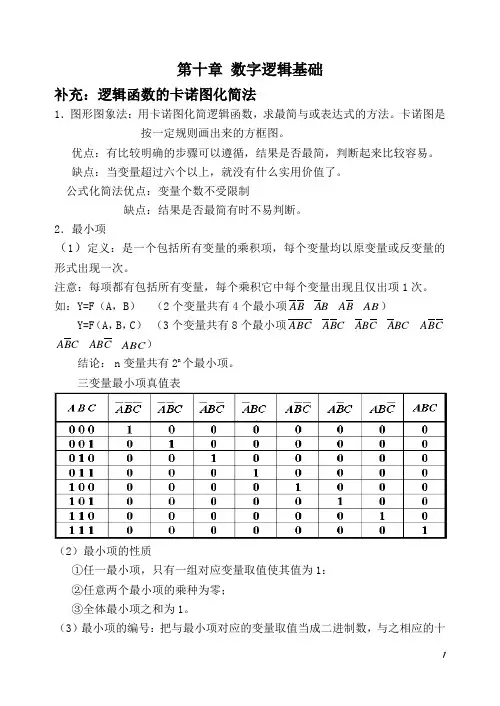
2．最小项（1）定义：是一个包括所有变量的乘积项，每个变量均以原变量或反变量的形式出现一次。

注意：每项都有包括所有变量，每个乘积它中每个变量出现且仅出项1次。

如：Y=F （A ，B ） （2个变量共有4个最小项B A B A B A AB ）Y=F （A ，B ，C ） （3个变量共有8个最小项C B A C B A C B A BC A C B AC B A C AB ABC ）结论： n 变量共有2n 个最小项。

三变量最小项真值表（2）最小项的性质①任一最小项，只有一组对应变量取值使其值为1： ②任意两个最小项的乘种为零； ③全体最小项之和为1。

（3）最小项的编号：把与最小项对应的变量取值当成二进制数，与之相应的十进制数，就是该最小项的编号，用m i 表示。

3．最小项表达式——标准与或式任何逻辑函数都可以表示为最小项之和的形式——标准与或式。

而且这种形式是惟一的，即一个逻辑函数只有一种最小项表达式。

例1．写出下列函数的标准与或式：Y=F(A,B,C)=AB+BC+CA 解：Y=AB(C +C)+BC(A +A)+CA(B +B)=ABC C B A ABC BC A ABC C AB +++++ =ABC C B A BC A C AB +++ =3567m m m m +++例2.写出下列函数的标准与或式：C B AD AB Y ++=解：))()(C B D A B A Y +++=（ ))((C B D B A ++= D C B C A B A B A +++=D C B A D C B A C B A C B A BC A ++++=D C B A D C B A D C B A D C B A D C B A D BC A BCD A ++++++=_ 8014567m m m m m m m ++++++= ＝）8,7,6,5,4,1,0(m ∑ 列真值表写最小项表达式。

电工电子技术-逻辑函数的化简


（2）吸收法
运用公式 A AB A 消去多余的项，其中，A、B可以是
任意一个复杂的逻辑式。例如：
Y1 AB AC DEB AB
Y2 AB ABC ABD AB D E AB AB C D D E AB
（3）消去法
运用公式 A AB A B 消去多余的因子。例如：
例如：逻辑函数Y的卡诺图。 Y ABCD ABCD ABCD ABCD
ABCD ABCD ABCD ABCD
（3）用卡诺图化简逻辑函数式 使用卡诺图化简逻辑函数所依据的原理是：具有相邻性 的最小项可以合并消去不同的因子。 ①2个相邻的最小项结合（用一个包围圈表示），可以消 去1个取值不同的变量而合并为1项，如下图所示。
00 01 11 10 00
01 11 10
②4个相邻的最小项结合（用一个包围圈表示），可以消 去2个取值不同的变量而合并为l项，如下图所示。
00 01 11 10 00
01 11 10
③8个相邻的最小项结合（用一个包围圈表示），可以消 去3个取值不同的变量而合并为l项，如下图所示。
00 01 11 10 00
②化简具有无关项的逻辑函数 在卡诺图中用×表示无关项。使用卡诺图化简逻辑函数 式时，要充分利用无关项可以当0也可以当1的特点，尽量扩 大卡诺圈，使逻辑函数式更简。
（2）卡诺图
卡诺图就是将n变量的全部最小项各用一个小方块表示，
并使具有逻辑相邻性的最小项在几何位置上也相邻的排列起 来所得的图形。下图所示为2到4变量最小项的卡诺图。
若要画出某一逻辑函数的卡诺图，只需将该逻辑函数式 化为最小项之和的标准形式后，在卡诺图中这些最小项对应 的位置上填入1，在其余的位置上填入0即可。
1．公式化简法

2、具有无关项的逻辑函数及


解：列真值表，见表1-20所示。
表1-20 例1-12的真值表
画卡诺图并化简。
5
图1-20 例1-12的卡诺图
利用无关项化简结果为：Y＝A＋BD＋BC 充分利用无关项化简后得到的结果要简单得 多。注意：当圈组后，圈内的无关项已自动取值 为1，而圈外无关项自动取值为0。
2012-11-2 6
例1-13化简逻辑函数 Y(A、B、C、D)= ∑m(1,2,5,6,9)+ ∑d(10,11,12,13,14,15) 式中d表示无关项。 解：画函数的卡诺图并化简。
2012-11-2 3
② 具有无关项的逻辑函数及其化简 因为无关项的值可以根据需要取0或取1，所以在 用卡诺图化简逻辑函数时，充分利用无关项，可以使 逻辑函数进一步得到简化。
2012-11-2
4
例1-12 设ABCD是十进制数X的二进制编码，当 X≥5时输出Y为1，求Y的最简与或表达式。
X A B 0 0 0 1 0 0 2 0 0 3 0 0 4 0 1 5 0 1 6 0 1 7 0 1 8 1 0 9 1 0 / 1 0 / 1 0 / 1 1 / 1 1 / 1 1 / 2012-11-2 1 1 C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 Y 0 0 0 0 0 1 1 1 1 1 × × × × × ×
1.3
1.3.5
逻辑函数及其化简
结束 放映
逻辑函数的卡诺图化简法
5. 具有无关项的逻辑函数及其化简
本章小结
2012-11-2
1
复习
卡诺图化简法的特点？步骤？ 什么叫逻辑相邻？ 正确圈组的原则？
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1.3
1.3.5
5.
逻辑函数及其化简
结束 放映
逻辑函数的卡诺图化简法
具有无关项的逻辑函数及其化简
本章小结
2018/8/2
1
复习
卡诺图化简法的特点？步骤？ 什么叫逻辑相邻？ 正确圈组的原则？
2018/8/2
2
5. 具有无关项的逻辑函数及其化简 ① 无关项的概念 对应于输入变量的某些取值下，输出函数的值可 以是任意的(随意项、任意项)，或者这些输入变量的取 值根本不会（也不允许）出现(约束项)，通常把这些输 入变量取值所对应的最小项称为无关项或任意项，在 卡诺图中用符号“×”表示，在标准与或表达式中用∑d （ ）表示。 例：当8421BCD码作为输入变量时，禁止码1010～ 1111这六种状态所对应的最小项就是无关项。
以上），则因为图形复杂，不宜使用。在实际化简
逻辑函数时，将两种化简方法结合起来使用，往往
效果更佳。
2018/8/2 10
作业题
1-13单
2018/8/2
11
或运算和非运算。
2018/8/2 8
逻辑函数有四种表示方法：真值表、逻辑表达式、
逻辑图和卡诺图。这四种方法之间可以互相转换，真
值表和卡诺图是逻辑函数的最小项表示法，它们具有 惟一性。而逻辑表达式和逻辑图都不是惟一的。使用 这些方法时，应当根据具体情况选择最适合的一种方 法表示所研究的逻辑函数。
2018/8/2
9
本章介绍了两种逻辑函数化简法。公式化简法
是利用逻辑代数的公式和规则，经过运算，对逻辑
表达式进行化简。它的优点是不受变量个数的限制， 但是否能够得到最简的结果，不仅需要熟练地运用 公式和规则，而且需要有一定的运算技巧。卡诺图 化简法是利用逻辑函数的卡诺图进行化简，其优点
是方便直观，容易掌握，但变量个数较多时（五个
图1-21 例1-13的卡诺图
2018/8/2
结果为：Y＝CD＋CD
7
本章小结
数字电路中广泛采用二进制，二进制的特点是
逢二进一，用0和1表示逻辑变量的两种状态。二进
制可以方便地转换成八进制、十进制和十六制。
BCD 码是十进制数的二进制代码表示，常用的 BCD码是8421码。 数字电路的输入变量和输出变量之间的关系可 以用逻辑代数来描述，最基本的逻辑运算是与运算、
2018/8/2 3
② 具有无关项的逻辑函数及其化简 因为无关项的值可以根据需要取 0 或取 1 ，所以在 用卡诺图化简逻辑函数时，充分利用无关项，可以使 逻辑函数进一步得到简化。
2018/8/2
ቤተ መጻሕፍቲ ባይዱ
4
例1-12 设ABCD是十进制数X的二进制编码，当 X≥5时输出Y为1，求Y的最简与或表达式。
X A B 0 0 0 1 0 0 2 0 0 3 0 0 4 0 1 5 0 1 6 0 1 7 0 1 8 1 0 9 1 0 / 1 0 / 1 0 / 1 1 / 1 1 / 1 1 / 2018/8/2 1 1 C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 Y 0 0 0 0 0 1 1 1 1 1 × × × × × ×
解：列真值表，见表1-20所示。
表1-20 例1-12的真值表
画卡诺图并化简。
5
图1-20 例1-12的卡诺图
利用无关项化简结果为：Y＝A＋BD＋BC 充分利用无关项化简后得到的结果要简单得 多。注意：当圈组后，圈内的无关项已自动取值 为1，而圈外无关项自动取值为0。
2018/8/2 6
例1-13化简逻辑函数 Y(A、B、C、D)= ∑m(1,2,5,6,9)+ ∑d(10,11,12,13,14,15) 式中d表示无关项。 解：画函数的卡诺图并化简。