逻辑代数及逻辑函数化简.doc
- 格式:doc
- 大小:1.20 MB
- 文档页数:21







笫二章逻辑函数及其简化一、选择题1.以下表达式屮符合逻辑运算法则的是—0A・C・Og B. 1+1=10 C. 0<1 D. A+l=l2.逻辑变量的取值1和0町以表示:_________ 。
A.开关的闭合、断开B.电位的高、低C.真与假D.电流的有、无3.当逻辑函数有n个变量时,共有 ______ 个变量取值组合?A. nB. 2n C・ r? D. 2n4.逻辑函数的表示方法屮具有唯一性的是 _______ 。
A •真值表 B.表达式 C.逻辑图D.卡诺图5.F二A B +BD+CDE+ A D= _______ 。
A. AB + DB. (A + B)DC. (A + D)(B + D)D. (4 + D)(B +万)6.逻辑函数1:二A㊉(A㊉8) = ___ oA.BB. AC. A㊉BD.勿㊉B7.求一个逻辑函数F的对偶式,可将F中的 _______ oA •“ •” 换成“ + ”,“ + ”换成“ •”B.原变量换成反变量,反变量换成原变量C.变量不变D.常数中“0”换成“1”,“1”换成“0”E.常数不变& A+BC 二____ oA . A+B B. A+C C. (A+B) (A+C) D. B+C9.在何种输入情况下,“与非”运算的结果是逻辑0。
—A.全部输入是0B.任一输入是0C.仅一输入是0D.全部输入是110.在何种输入情况下,“或非”运算的结果是逻辑0。
—A.全部输入是0B.全部输入是1C.任一输入为0,其他输入为1D.任一输入为1二、判断题(正确打J,错误的打X)1.逻辑变量的取值,1比0大。
()。
2.异或函数与同或函数在逻辑上互为反函数。
()。
3.若两个函数具有相同的真值表,则两个逻辑函数必然相等。
()o4.因为逻辑表达式A+B+AB二A+B成立,所以AB=O成立。
()5.若两个函数具有不同的真值表,则两个逻辑函数必然不相等。
()6.若两个函数具有不同的逻辑函数式,则两个逻辑函数必然不相等。


常用逻辑函数表示方法有:1、逻辑真值表2、逻辑表达式3、逻辑图各种表示方法间的相互转换4、工作波形图常用逻辑函数表示形式:1、逻辑函数的八种表示形式2、逻辑函数的标准表示形式标准表示形式间的相互转换= A利用代入规则:五、综合法 合并项法、吸收法、消去法、配项法。
F = AD + A D + AB + AC + BD + ACEF + BEF + DEFG= A(D + D ) + AB + AC + BD + ACEF + BEF = A(1 + B + CEF ) + AC + BD + BEF = A + AC + BD + BEF 加对乘分配率:A + AC = ( A + A)( A + C ) = A + C + BD + BEFF = A( A + B )( A + C )( B + D )( A + C + E + F )(B + F )( D + E + F ) 解:首先将或-与表达式通过求对偶变为与-或表达式,利用 公式法在与-或表达式中进行化简。
(分配率) ' F = A + AB + AC + BD + ACEF + BF + DEF (合并项) = A + AC (1 + EF ) + BD + BF (包含率)= A + AC + BD + BF (分配率) = A + C + BD + BF第二步:将对偶式再次求对偶,得到原函数的最简或-与式。
F = F = AC ( B + D )(B + F )''代数化简法优点 : 不受变量限制。
缺点:化简方向不明确,一般采用试凑法,要有一定技巧。
对于任何一个逻辑函数的功能描述都可以作出真值表,根 据真值表可以写出该函数的最小项之和及最大项之积的形式。
例:F = A ⊕ B真值表A 0 0 1 1 B 0 1 0 1 F F = 1 的输入变量组合有 AB = 01、10 两组。
= m1 + m 2 = ∑ (1.2 ) 最小项之和: F = A B + A B 0 1 F = 0 的输入变量组合有 AB = 00、11 两组。

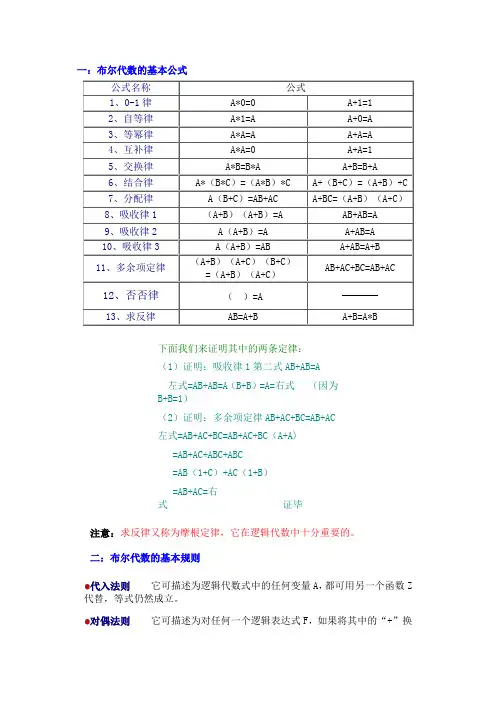
一:布尔代数的基本公式公式名称公式1、0-1律A*0=0 A+1=12、自等律A*1=A A+0=A3、等幂律A*A=A A+A=A4、互补律A*A=0 A+A=15、交换律A*B=B*A A+B=B+A6、结合律A*(B*C)=(A*B)*C A+(B+C)=(A+B)+C7、分配律A(B+C)=AB+AC A+BC=(A+B)(A+C)8、吸收律1(A+B)(A+B)=A AB+AB=A9、吸收律2A(A+B)=A A+AB=A10、吸收律3A(A+B)=AB A+AB=A+B11、多余项定律(A+B)(A+C)(B+C)=(A+B)(A+C)AB+AC+BC=AB+AC12、否否律()=A13、求反律AB=A+B A+B=A*B下面我们来证明其中的两条定律:(1)证明:吸收律1第二式AB+AB=A左式=AB+AB=A(B+B)=A=右式(因为B+B=1)(2)证明:多余项定律AB+AC+BC=AB+AC左式=AB+AC+BC=AB+AC+BC(A+A)=AB+AC+ABC+ABC=AB(1+C)+AC(1+B)=AB+AC=右式证毕注意:求反律又称为摩根定律,它在逻辑代数中十分重要的。
二:布尔代数的基本规则代入法则它可描述为逻辑代数式中的任何变量A,都可用另一个函数Z 代替,等式仍然成立。
对偶法则它可描述为对任何一个逻辑表达式F,如果将其中的“+”换成“*”,“*”换成“+”“1”换成“0”,“0”换成“1”,仍保持原来的逻辑优先级,则可得到原函数F的对偶式G,而且F与G互为对偶式。
我们可以看出基本公式是成对出现的,二都互为对偶式。
反演法则有原函数求反函数就称为反演(利用摩根定律),我们可以把反演法则这样描述:将原函数F中的“*”换成“+”,“+”换成“*”,“0”换成“1”,“1”换成“0”;原变量换成反变量,反变量换成原变量,长非号即两个或两个以上变量的非号不变,就得到原函数的反函数。
第 2 章逻辑代数和逻辑函数化简基本概念:逻辑代数是有美国数学家 George Boole 在十九世纪提出 , 因此也称布尔代数 , 是分析和设计数字逻辑电路的数学工具。
也叫开关代数, 是研究只用 0 和1 构成的数字系统的数学。
基本逻辑运算和复合逻辑运算基本逻辑运算:“与”、“或”、“非”。
复合逻辑运算:“与非”、“或非”、“与或非”、“异 或”、“同或”等。
AB基本逻辑运算~ 220VF1. “与”运算①逻辑含义:当决定事件成立的所有条件全部具备时,事件才会发生。
②运算电路:开关 A 、B 都闭合,灯 F 才亮。
③表示逻辑功能的方法:真值表A B F 灯 F 的状态代表 开关 A 、B 的状态代0 0表输入:0 1 0 输出:1 0 0 “ 0”表示亮;“0”表示断开;111表达式: F A B= ? 逻辑符号:A &FA FA FBBB国家标准 以前的符号欧美符号功能说明: 有 0 出 0,全 1 出 1。
在大规模集成电路可编程逻辑器件中的表示符号:A BA BA B&FFF通过“ ?”接入到此线上的输入信号都是该与门的一个输入端。
推广:当有 n 个变量时: F=A 1A 2 A 3 ? ? ? A n “与”运算的几个等式:0?0=0,0?1=0, 1?1=1A?0=0(0-1 律), A?1=A (自等律),A?A=A (同一律), A?A?A=A (同一律)。
2. “或”运算①逻辑含义:在决定事件成立的所有条件中,只要具备一个,事件就会发生。
A②运算电路: 开关 A 、B 只要闭合一个,灯 F 就亮。
B~220VF③表示逻辑功能的方法:逻辑功能: 有 1 出 1,全 0 出 0。
真值表:(略)表达式: F=A+B逻辑符号:A≥ 1FA FAFB+BB国家标准以前的符号欧美符号推广:当有 n 个变量时: F=A 1+A 2+ A 3+? ? ? +A n“或”运算的几个等式:0+0=0,0+1=1, 1+1=1A+0=A (自等律) A+1=1( 0-1 律),A+A=A (同一律)。
上次课小结:与、或的功能、表达式等,几个等式。
3.“非”运算①逻辑含义:当决定事件的条件具备时, 事件不发生;当条件不具备时,事件反而发生了。
R②运算电路:开关 A 闭合,灯 F 不亮。
~ 220VAF③表示逻辑功能的方法:逻辑功能: 入 0 出 1,入 1 出 0。
真值表:(略)表达式: F= A逻辑符号:A1F AF AF国家标准以前的符号欧美符号“非”运算的几个等式:A =A (还原律);A+ A =1、AA =0(互补律)。
2.1.2复合逻辑运算1.“与非”运算“与”和“非”的组合。
有专门实现这种运算的实际器件(如TTL 与非门等)。
逻辑符号:A &FA FA FBBB国家标准以前的符号欧美符号表达式: F= AB ;真值表:(略),逻辑功能为: 有 0 出 1,全 1 出 0。
2.“或非”运算“或”和“非”的组合。
也有专门实现这种运算的实际器件(如TTL 、 CMOS 与非门等)。
逻辑符号:A≥1FA FAFB+BB国家标准 以前的符号欧美符号表达式: F= A B ;真值表:(略),逻辑功能为: 有 1 出 0,全 0 出 1。
3.“与或非”运算逻辑符号:A & ≥ 1AAB FB FB FCC +CDDD国家标准 以前的符号 欧美符号表达式: F= AB CD ;真值表:(略)。
4.“异或”运算逻辑功能:两变量状态 相异出 1,相同出 0。
真值表:(略)。
表达式: F=A B= A B + A B逻辑符号:A =1A A BFFFBB国家标准以前的符号欧美符号“异或”运算的几个等式:A0 = A ;A 1 = A ;A;AAA =1 = 05.“同或”运算逻辑功能:两变量状态 相异出 0,相同出 1。
逻辑符号:A =1A FA BF⊙FBB国家标准 以前的符号欧美符号与“异或” 运算正好相反, 也称“异或非” 运算。
“异或” 运算的几个等式 (略)。
逻辑代数的基本定律及规则2.2.1 逻辑代数的基本定律或者称为基本公式:0-1 律: 1· A=A ; 0+A=A 。
0· A=0; 1+A=1。
交换律: AB=BA ; A+B=B+A 。
结合律: A ( BC )=(AB ) C ; A+(B+C ) =( A+B )+C 。
分配律: A ( B+C )=AB+AC ;A+BC=( A+B )( A+C )。
互补律: A A =0;A+ A =1。
重叠律: AA=A ; A+A=A 。
还原律: A =A ; 反演律: AB = AB ; AB = A B吸收律 1: A+AB= A ; A (A+B ) = A 。
吸收律 2: A+ A B= A+B ; A ( A +B ) = AB 。
吸收律 3: AB+ A B = A ;(A+B )(A+ B )= A 。
冗余定理: AB+ A C+BC= AB+ A C ;(A+B )( A +C )(B+C )=(A+B )( A +C )。
证明:左边 =AB+ A C+BC (A+ A )= AB+ A C+ABC+ A BC= AB ( C ) + A C ( B ) = AB + A C=右边(证毕)1+ 1+冗余定理指出:当某变量以互补形式出现在两个与项中时,这两个与项的其余因子组成的第三项为多余项。
推论:ABC+BCf( a ,b ,,⋯ = ABC+ Ac )+ A多余项2.2.2 逻辑代数的基本规则1.代入规则将逻辑等式中的某一变量都代之以另一个逻辑函数,此等式仍成立。
例: AB = A B 。
用 BC 代替等式中的 B 得A( BC ) = A BC = A B C反复运用代入规则可得:ABCD= A B C D。
扩大了等式的应用范围。
2.对偶规则如果将任一逻辑函数式 F=f ( A ,B ,C ,⋯ ) 中所有的·换成 +所得到的新函数 F ˊ就是 F 的对偶式。
此即对偶规+ 换成 ·则。
运用时 注意:0 换成 11 换成 0①原运算顺序不变(可运用扩号保证) 。
例:求 FCD (C D) B 的对偶式。
= AB B解: F =[( A B) B(C D)] (C D B)F 与F 互为对偶, ( F ) F 。
=还要注意到: 对偶关系不是相等的关系,即 F ≠F 。
运用对偶规则可以使要记忆的公式减少一半。
观察 P27 中的基本公式可以发现,只要记住左半部分,运用对偶规则就能得到右半部分。
3.反演规则如果将任一逻辑函数式F=f( A,B,C,⋯ ) 中所有的·换成 ++换成·0换成 11换成 0原变量换成反变量反变量换成原变量所得到的新函数 F 就是 F 的反函数。
此即反演规则。
运用时注意:①原运算顺序不变(可运用扩号保证)。
②原式的公共非号保持不变。
例:求 F=( A B C D ) E 的反函数。
解: F = A (B C D) E公共非号也可以改变,但在消去公共非号的同时,公共非号下面的子函数保持原状。
如上例:F A (B C? D) E ,与F A ( B C D) E 相等。
(应用摩根定律)从原函数求反函数的过程叫做反演。
摩根定律是进行反演重要工具。
例如,将 F=( A B C D ) E 两边同时取反并反复运用摩根定律的:F = ( A B C D ) E = (A B C D ) E = A B C D E = A ( B C D ) E当函数较简单时,可以用摩根定律求反,当函数比较复杂时,用反演规则求反比较方便。
逻辑函数的表示方法及其转换除用文字描述以外,还有四种描述形式:真值表、表达式、卡诺图、逻辑图2.3.1逻辑表达式完备函数的概念:我们已经学习过三种最基本的逻辑运算:逻辑与;逻辑或;逻辑非,用他们,可以解决所有的逻辑运算问题,因此可以称之为一个“完备逻辑集”。
一. 逻辑表达式的类型每种函数对应一种逻辑电路。
同一个函数逻辑有多种表达形式:F AC AB = AC BC AAC (A B) A ( A B) (冗余定理 、互补律) = + + + A B = = ( A B)( A C )= AC AC← AC A B (还原律、摩根定律) = A B AC← ( A B)(AC ) (还原律、摩根定律)= AC AB = AB AC← (A B)( A C ) (反演规则再求反)= ABCABC A BC A BC← AC A B = AC ( B B ) AB(C C )用互补律配项二.逻辑函数的标准形式1.最小项( 1)定义:对于 N 个变量,如果 P 是一个含有 N 个因子的乘积项,而且在 P 中每个变量都以原变量或反变量的形式作为一个因子出现,且仅出现一次,则称P 是N 个变量的一个最小项。
简单地说:最小项就是包含全部变量的与项。
例如:AB C 、 AB C 、 ABC 、 A BC 、 AB C 、 AB C 、 ABC 、 ABC 都是三个变量的最小项。
而 A B 、 AB 、 AB 、AB 都是两个变量的最小项,而对于三个或者三个以上的变量来说,它们就是一般乘积项。
所以:提及最小项一定要说明变量的数目。
N 个变量共有 2n 个最小项。
(2) 性质取三个变量的全体最小项观察:A BC 、 ABC 、 ABC 、 ABC 、 AB C 、 AB C 、 ABC 、 ABC对应的取值组合: 000 001 010 011 100 101 110 111①每个最小项都对应了一组变量取值。
对任一最小项,只有与之对应的那一组变量取值才是它的值为“1”;②任意两个不同最小项之积恒为 0;③全体最小项的逻辑和恒为 1;④两个逻辑相邻的最小项可以合并为一项,从而消去一个因子。
(3) 最小项标准表达式任何一个逻辑函数都能表示成最小项之和的形式, 而且这种表示形式是唯一的,这就是标准与或式, 也叫最小项标准表达式。
由一般式→标准与或式 的变换步骤: ①用公式把一般式化为一般与或式;②若式中的某一项缺少某个变量,就用该变量的原变量和反变量之和去乘这一项,然后拆成两项,直到补齐所缺变量为止。
例:写出 F= ABB C 的标准与或式。
(F= AB B C = ABACB C )解: ①化为一般与或式F A B B C 冗余=②补齐所缺变量 F = A B(C C ) BC ( A A ) = A BC AB C A BC ABC也可以由 F ABBC 列出真值表,直接写出最小项标准表达式。
=最小项标准表达式的另一种表示形式:A BC 、 ABC 、 ABC 、 ABC 、 AB C 、 AB C 、 ABC 、 ABC对应的取值组合: 000 001 010 011 100 101 110 111 二进制换十进制123 4 5 6 7记为m 0m 1m 2m 3m 4m 5m 6 m 7F A BCAB CA BCABC 还可以表示成:=m 4 m 3 m 2 F ∑m ( , , , ) F m 0+ + + 或者写成= = 0 2 3 4根据逻辑函数的特点, 这种表示方法 ①便于转换成卡诺图; ②便于写出反函数。