材料力学专题一梁的内力和内力图

格式：doc
大小：1.18 MB
文档页数：6

下载文档原格式

/ 6

材料力学专题一梁的内力和内力图

专题一梁的内力和内力图例1求图1(a)所示梁截面 A 、C 的剪力和弯矩。

解：1）求反力kN 5=A F ，kN 4=B F2）求A 左截面的内力，如图(a)所示。

0=∑i Y ， 0=+左SA p F F ，kN 3-=左SA F0=∑O M ，02=+⨯左A p M F ， m kN 6⋅-=左A M3）求A 右截面的内力，如图(b)所示。

0=∑i Y ，0=+--A SA p F F F 左，kN 2=左SA F0=∑O M ，02=+⨯右A p M F ， m kN 6⋅-=右A M4）求C 左截面的内力，如图(c)所示。

0=∑i Y ，02=-⨯--左SC P A F q F F ，0=左SC F0=∑O M ，01224=+⨯⨯+⨯-⨯左C A p M q F F ，=左C M m kN 4⋅-=5）求C 右截面的内力，如图(d)所示。

0=∑i Y ，02=-⨯--右SC P A F q F F ，0235=--=右SC F 0=∑O M ，012241=++⨯⨯+⨯-⨯右C A p M M q F F ，=右C M m kN 6⋅-=【小结】①求指定截面上的内力时，既可取梁的左段为脱离体，也可取右段为脱离体，两者计算结果一致。

一般取外力比较简单的一段进行分析。

②在解题时，通常假设截面上把内力为正，若最后计算结果是正，则表示假设的内力方向（转向）与实际是相同的，否则是相反的。

③该题也可以不画受力图，不写平衡方程而由前面的结论直接求得结果。

图1(a)(b)(c)(d) (e)例2试计算图2所示各梁指定截面（标有细线者）的剪力与弯矩。

解：(a)取A +截面左段研究，, 0SA A F F M ++==取C 截面左段研究，, 2SC C Fl F F M == 取B -截面左段研究， , SB BF F M Fl ==(b) 求A 、B 处约束反力如图(d)所示，l M F F e B A /==取A +截面左段研究，, e SA A A e M F F M M l++=-=-=取C 截面左段研究，, 22e e SC A A e A M Ml F F M M F l +=-=-=-⨯=取B 截面右段研究，, 0e SB B B MF F M l=-=-=(c) 求A 、B 处约束反力取A +截面右段研究，233, 22248SA A l ql l l ql F q M q ++=⨯==-⨯⨯=-取C -截面右段研究，2, 22248SC C l ql l l ql F q M q --=⨯==-⨯⨯=-取C +截面右段研究，2, 22248SC C l ql l l ql F q M q ++=⨯==-⨯⨯=-取B -截面右段研究，0, 0SB B F M --==图2 (b) (a) qB (c) B图(d)例3试写出图3所示梁的内力方程，并画出剪力图和弯矩图。

第6章-梁的内力PPT课件

l ql l M CLM Cq4L l2 FA2240
（3）计算截面C稍右处的剪力FsR、弯矩MCR。
M C
MCR
A
l/2
FA
Fy 0
FsR
ql FsRFA2 0
MCF0
解之得：
FsR
ql 4
M CR MFA2 lq 2 l4 l0
精选PPT课M件CR 0
14
建筑力学
❖ 计算剪力和弯矩的规律
(1) 梁内任一截面上的剪力，其大小等于该截面左侧(或右侧) 梁上所有外力的代数和；梁内任一截面的弯矩，其大小等于该截面左侧(或右侧)梁上所有外力对于该截面形心之矩的
★ 由平衡方程 F得y ，0
F s x F s x d s x F q x d 0 x
dFsx qx
dx
（9-1）
几何意义：剪力图上某点处的切线斜率等于该点处荷载
集度的大小。
精选PPT课件
23
建筑力学
★ 由平衡方程 MC 得，0
M x dx M M x F sx d q x x d d 2 x 0 x
(3)列出各段的剪力方程和弯矩方程：各段列剪力方程和弯矩方程时，所取的坐标原点与坐标轴x的正向可视计算方便而定，不必一致。
(4) 画剪力图和弯矩图：先根据剪力方程(或弯矩方程)判断剪力图(或弯矩图)的形状，确定其控制截面，再根据剪力方程(或弯矩方程)计算其相应截面的剪力值(或弯矩值)，然后描点并画出整个全梁的剪力图(或弯矩图)
解之得： Fs 4kN 精选PPTM 课件144 kNm
12
[例]
简支梁受均布荷载q和集中力偶M=ql2/4的作用，如图所示。求截面C 的剪力和弯矩。
M
q

材料力学内力与内力图.

由 M A 0得
5
RA
74
qa
RB 4 qa
（2）求剪力与弯矩
FQ1 RA 5qa / 4 M 2 M1 RA a 5qa2 / 5
FQ3 FQ2 RA qa qa/ 4
M 3 2aRA qa a 3qa2 / 2
FQ4 qa RB
3qa 4
,
M4
5qa 2 4
图
(3) 弯矩的数值标在受拉边，轴力、
刚架
剪力画在里侧和外侧均可，但需标出正负号；
内力
(4) 注意节点处的平衡关系。
图
例:绘刚架内力图
解：一）求支反力：
MA 0:
8kN
1m D
2m C
E
q=1kN/m 4m 3m
RB
81 811 3
5kN
X 0:
4q RAx 1 0 RAx 3k N
静定梁的基本形式1求支反力211面上的内力梁的剪力与弯矩剪力弯矩剪力f的符号规定弯矩m的符号规定左上右下为正上压下拉上凹下凸为正例61求梁112233和44截面上的剪力和弯矩
弯曲内力
§6-1对称弯曲的概念及梁的计算简图
一. 弯曲的概念
1.工程实例桥梁，屋梁，车轴都是最常见梁的例子。 2.定义
当作用在杆件上的载荷和支反力都垂直于杆件轴线时，杆件的轴线因变形由直线变成了曲线，此变形称为弯曲变形。
N3 RAy 3k N Q( x3 ) RAx qx3
8kN
DN13m
2m C
M (x3 ) EQ( x3X)2
q=1kN/m 4Xm3 3m
(3) 1x3 3 x3
M
( x2
)
RAx x3
1 2

第六章梁的内力图--剪力图和弯矩图

第三节梁的内力图—剪力图和弯矩图(1)
一、列剪力方程、弯矩方程，作梁的剪力图、弯矩图梁内各截面上的剪力和弯矩一般都随截面的位置而变化，以横坐标 x表示梁横截面的位置，反映梁的剪力、弯矩值随 x值变化的方程分别就是剪力方程 Q(X) 和弯矩方程 M(X)。
根据剪力方程和弯矩方程可分别绘制剪力图和弯矩图，其画法与轴力图相似。用平行于梁轴的坐标 x表示横截面的位置，垂直于梁第六轴的纵坐标表示相应截面的剪力或弯矩。一般习惯把正剪章建直力画在 X 轴的上方，负剪力画在 X 轴下方；而把弯矩图画在筑梁力弯梁受拉的一侧。学曲
第六章直梁弯曲
建筑力学
第三节梁的内力图—剪力图和弯矩图(1)
第六章直梁弯曲
建筑力学
第三节梁的内力图—剪力图和弯矩图(1)
第六章直梁弯曲
建筑力学
第三节梁的内力图—剪力图和弯矩图(1)
第六章直梁弯曲
建筑力学
第三节梁的内力图—剪力图和弯矩图(1)
建筑力学
第三节梁的内力图—剪力图和弯矩图(1)
二、在集中力偶作用下梁的内力图：例6－6简支梁AB在C截面处作用有集中力偶m(如图)，试画出梁的剪力图和弯矩图
绝对值等于该集中力偶的力偶矩。
第六章直梁弯曲
建筑特点：在集中力偶作用处V图无变化，M图发生突变，突变的力学
第三节梁的内力图—剪力图和弯矩图(1)
建筑力学
第三节梁的内力图—剪力图和弯矩图(1)
在集中力作用下梁的内力图的特点：在梁上只有集中力作用时，集中力把梁分为若干段无荷载作用区。在无荷载作用区：V图是与x轴平行的直线；M图是斜直线。在集中力作用处：V图发生突变，突变的绝对值等于该集中力；M图发生转折。

建筑力学材料力学梁的内力

x
②写出内力方程 Q( x ) YO P
M ( x) YO x M O P( x L)
x
③根据方程画内力图。
q
解：①写出内力方程
L Q(x) ○ x – qL
qL2 2
Q( x ) qx
1 M ( x ) qx2 2
②根据方程画内力图
⊕ M(x) x
x
Q(x)
2
106 .30 1.855rad
3.14 1 0.01 7800 9.8 [3.14 0.52 1 0.52(1.855 sin106.3)] 1000 9.8 2
9 (kN/m)
q — 均布力
§4–3 一、弯曲内力：
举例
梁的内力及其求法
目
录
§4–1 工程中的弯曲问题 §4–2 梁的荷载和支座反力 §4–3 梁的内及其求法 §4–4 内力图 — 剪力图和弯矩图
§4–5 弯矩、剪力、荷载集度间的关系
§4–1 工程中的弯曲问题一、弯曲的概念
1. 弯曲: 杆受垂直于轴线的外力或外力偶矩矢的作用时,轴线变成了曲线，这种变形称为弯曲。 2. 梁：以弯曲变形为主的构件通常称为梁。
mB (Fi ) 0 , 1 2 qLx2 M 2 q( x2 a) 0 2
图（a） B M2 x2 Q2
1 M 2 q( x2 a)2 qLx2 2
图（c）
§4–4 内力图 — 剪力图和弯矩图
一、内力方程：内力与截面位置坐标（x）间的函数关系式。
Q Q( x ) M M (x)
Q Q 图特征
水平直线
Q Q
斜直线
Q

梁的内力图2-2-3-1

注：最后利用规律3、4、5校核规律3 规律
例：画出 V图和 M 图。图和解：1、求反力由∑MA= 0，FB= 148 kN. ， ∑MB= 0，FA= 72 kN. ， 2、判断各段V、M图形状判断各段V 分段 q V M AC q=0 水平线斜直线 CB q=c＜0 ＜下斜直线下凸曲线下凸曲线 BD q=c＜0 ＜下斜直线下凸曲线下凸曲线 A FA
0
画剪力图和弯矩图时，一定要将梁正确分段，画剪力图和弯矩图时，一定要将梁正确分段，分段建立方程，分段建立方程，依方程而作图。
0 x x
M
二、列方程法画内力图（基本方法）列方程法画内力图（基本方法）列方程法画内力图例：简支梁受均布荷载作用，如图示，简支梁受均布荷载作用，如图示，作此梁的剪力图和弯矩图。作此梁的剪力图和弯矩图。解：1 、求支座反力 (利用结构对称利用结构对称性简化计算；性简化计算；悬臂结构可不求反力）
2
、剪力图和弯矩图
以梁横截面沿梁轴线的位置为横坐标，以梁横截面沿梁轴线的位置为横坐标，以垂直于梁轴线方向的剪力或弯矩为纵坐标，于梁轴线方向的剪力或弯矩为纵坐标，分别绘制表示V(x) M(x)的图象 V(x)和的图象。制表示V(x)和M(x)的图象。这种图象分别称为剪力图和弯矩图，简称V图和M 剪力图和弯矩图，简称V图和M图。绘图时一般规定正号的剪力画在x轴的上侧，绘图时一般规定正号的剪力画在x轴的上侧，负号的剪力画在x轴的下侧；正弯矩画在x 负号的剪力画在x轴的下侧；正弯矩画在x轴下负弯矩画在x轴上侧，即把弯矩画在梁受侧，负弯矩画在x轴上侧，即把弯矩画在梁受拉的一侧。拉的一侧。 V
A FA V
(kN)
1

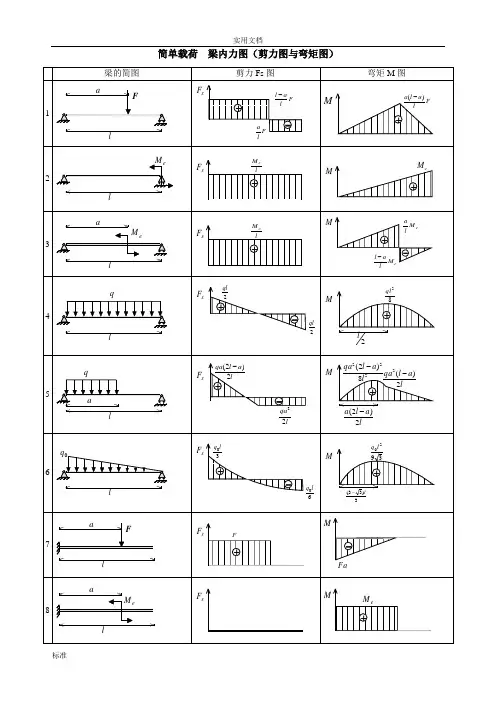
梁弯矩图梁内力图 (剪力图与弯矩图)

简单载荷梁内力图（剪力图与弯矩图）表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注：力边界条件即剪力图、弯矩图在该约束处的特征。

常用截面几何与力学特征表表2-5标准标准标准标准标准标准标准注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）。

基本计算公式如下：⎰•=AdA yI 22．W 称为截面抵抗矩（mm 3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：maxy I W =3．i 称截面回转半径（mm ），其基本计算公式如下：AIi =4．上列各式中，A 为截面面积（mm 2），y 为截面边缘到主轴（形心轴）的距离（mm ），I 为对主轴（形心轴）的惯性矩。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

实用文档2．单跨梁的内力及变形表（表2-6~表2-10）（1）简支梁的反力、剪力、弯矩、挠度表2-6（2）悬臂梁的反力、剪力、弯矩和挠度表2-7（3）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8（4）两端固定梁的反力、剪力、弯矩和挠度表2-9（5）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的内力及变形表（1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14）1）二跨等跨梁的内力和挠度系数表2-11注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

[例1] 已知二跨等跨梁l ＝5m ，均布荷载q ＝11.76kN/m ，每跨各有一集中荷载F ＝29.4kN ，求中间支座的最大弯矩和剪力。

[解] M B 支＝（－0.125×11.76×52）＋（－0.188×29.4×5）＝（－36.75）＋（-27.64）＝－64.39kN ·m V B 左＝（－0.625×11.76×5）＋（－0.688×29.4）＝（－36.75）＋（－20.23）＝－56.98kN[例2] 已知三跨等跨梁l ＝6m ，均布荷载q ＝11.76kN/m ，求边跨最大跨中弯矩。

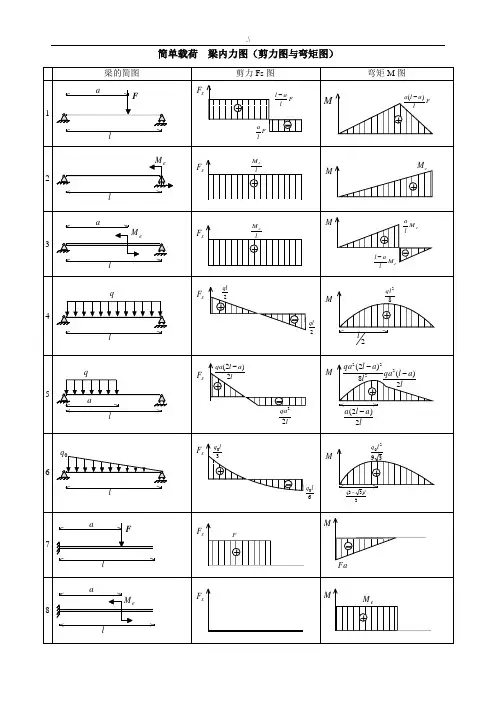
梁弯矩图梁内力图(剪力图与弯矩图)

常用截面几何与力学特征表表2-5注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

.\2．单跨梁的内力及变形表（表2-6~表2-10）（1）简支梁的反力、剪力、弯矩、挠度表2-6（2）悬臂梁的反力、剪力、弯矩和挠度表2-7（3）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8（4）两端固定梁的反力、剪力、弯矩和挠度表2-9（5）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的内力及变形表（1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14）1）二跨等跨梁的内力和挠度系数表2-11注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

[例1] 已知二跨等跨梁l ＝5m ，均布荷载q ＝11.76kN/m ，每跨各有一集中荷载F ＝29.4kN ，求中间支座的最大弯矩和剪力。

建筑力学第4章内力和内力图

建筑力学
内力和内力图
38
§4-3 扭矩和扭矩图
A l
B
建筑力学
内力和内力图
39
如上图所示，杆件在横向平面内的外力偶作用下发生扭转变形。其侧面上原有的直线ab变为螺旋线ab′, 诸横截面绕杆的轴线相对转动，例如B截面相对于A截面转过一角度∠bO'b′。为了分析横截面上的内力，取m--m截面。
建筑力学
内力和内力图
1
第 4 章内力和内力图
§4-1 平面桁架的内力 §4-2 轴力和轴力图 §4-3 扭矩和扭矩图 §4-4 剪力和弯矩·剪力图和弯矩图
建筑力学
内力和内力图
2
外力：物体或系统所承受的其它物体对它的作用力（包括约束力）。内力：物体或系统内部，因外力作用而产生的各物体之间或各部分之间的相互作用力。内力必然成对存在，它们是大小相等、指向相反的力，或大小相等、转向相反的力偶。为了求得物体内部各部分之间的相互作用力，需将物体假想地截开，取其一部分来研究；对于系统，也须截取某一部分来研究。
内力和内力图
19
2. 截面法
例题 4-2
F A a a C FC E FE a D a B
如图平面桁架，已知铅垂力FC = 4 kN，水平力FE = 2 kN。求FE， CE，CD杆内力。
建筑力学
内力和内力图
20
例题 4-2
解：先取整体为研究对象,受力如图所示。由平衡方程
FAy A FAx
F a a
建筑力学
内力和内力图
33
例题 4-3
3 30 kN A 2 20 kN 1 1 20kN D 20kN D 20kN 30 kN B 20 kN C D B 2 FN2

内力与内力图

常见载荷作用下剪力图和弯矩图的特点
若一段梁上无载荷（即q=0），则剪力图为水平直线，弯矩图为倾斜直线。剪力为正时，弯矩图为向右上方倾斜的直线，剪力为负时则弯矩图向右下方倾斜，剪力为零时弯矩图成为水平直线。若一段梁上作用着均布载荷，则剪力图为斜直线，弯矩图为二次抛物线。若均布力方向向下，则剪力图为向右下方倾斜的直线，弯矩图为开口向下的抛物线，抛物线的顶点的剪力等于零的截面。在集中力作用的截面上，剪力图有突变，变化值等于该集中力的大小，弯矩图上由出现折角。在集中力偶作用的截面上，剪力图无变化，弯矩图上有突变，变化值等于该集中力偶的力偶矩的大小。
2
ql
五弯矩、剪力与载荷集度间的关系
在例3中，将弯矩方程对x求一阶导数，得
dM qx F Q dx
将剪力方程对x求一阶导数，得
dF Q dx
q
也就是说，弯矩方程对x的一阶导数等于剪力方程；剪力方程对x的一阶导数等于载荷集度。这一关系并非只存在于该问题中，而是普遍成立的一个规律。根据导数的几何意义，以上关系表明：弯矩图上某点的切线的斜率，等于对应截面上的剪力；剪力图上某点切线的斜率等于对应截面上的载荷集度。根据这一规律，还可得到常见载荷下剪力图和弯矩图的特点。
例4
例4 外伸梁受力如图所示，试画出其剪力图和弯矩图。
解：（1）根据梁的平衡条件求出梁的支座反力。
FA
qa 4
FB
3qa 4

例1 杆件受力如图所示,求指定截面上的轴力并画出轴力图。
• • • • • • • • • • • • • • 解：（1）用截面法求内力。沿截面1-1截开，由左侧一段的平衡，有 FN1+10=0 所以 FN1=-10（kN）沿截面2-2截开，由左侧一段的平衡，有 FN2-40+10=0 所以 FN2=40-10=30（kN）沿截面3-3截开，由右侧一段的平衡，有 -FN3+20=0 所以 FN3=20（ kN ）（2）根据计算结果作出轴力图。（3）讨论：由以上计算过程可以看出，将平衡方程中的外力都移至等号右端，则有 FN=ΣFie 也就是说，横截面上的轴力，等于其左侧（或右侧）一段杆上所有外力的代数和。掌握这一关系，有利于快速计算轴力并画出轴力图。

材料力学-内力与内力图

结论直梁某横截面上的弯矩等于该截面一端（左或右端）
全部力偶矩及全部作用力(包括支反力)对该截面矩的代数和。
MI m(F, q, Me ) （左顺右逆取＋号，反之取负号）
26
例3 求承受均布荷载作用的简支梁的内力方程，并画出相应的剪力图和弯矩图。 1 [ 解] （1）先求支反力 RA R qL [解] B A B y 2 （2）求梁的内力方程 q M 1 x FSS qL qx 剪力 2 x FS S 所有力对截面形心的力矩平衡 L qL / 2 m0 1 2 1 qx 2 qLx M ( x) 0 2 2 1 弯矩 M ( x) qx( L x) 2 结论直梁某横截面上的弯矩等于该截面一端（左或右端）全部力偶矩及全部作用力(包括支反力)对该截面矩的代数和。
准确理解杆件内力的定义和符号规定。能利用截面法建立内力方程，能迅速求出指定截面的内力。深入理解梁中弯矩、剪力和分布荷载之间的微分关系，并能利用这些关系熟练地画出梁的剪力弯矩图；能正确画出刚架、曲杆的内力图。
4
2.1 内力 ( internal forces ) 定义和符号规定定义和符号规定
0,
M
z z
0
T T ( x), M yy M yy( x), M zz M zz( x).
由内力方程作出杆件的内力图
(a x b) —作内力图的列方程法
14
2.2 内力方程及内力图
用截面法求内力方程方法和步骤－“截面法”
“切” 、（“留 ”)、“代”、“平”
1) 在必要和可能的条件下，先求出所有约束的反力。 2) 在要求内力的截面位置，用一假想截面将杆件切开。（留下一部分作为研究对象，舍去另一部分) 下一部分作为研究对象，舍去另一部分 3) 舍去部分对留下部分的作用代之以相应的力 ( 即为要求的舍去部分对留下部分的作用 (即为要求的内力 ) 。将这种内力作用的方向按假设为正内力方向（即设内力) 正法）画在截面上。 4) 留下部分的所有内力、外力（包括约束反力）按照理论力学的符号规定建立力或力矩的平衡方程式。 5) 求解方程即可得内力。若所得内力为负值，表明实际内力方向与设想方向相反。 15

14-梁的内力及梁的内力图

x
B FB CB段（x > a）时 M2(x) FS2(x) FB
AC段（x < a）时 M1(x) FA
x
FS1(x)
Fb (0 < x < a ) FS1 ( x ) = l
Fb M 1 (x ) = x (0 ≤ x ≤ a ) l
Fa (a < x < l ) FS2 ( x ) = − FB = − l Fa (l − x ) M 2 ( x ) = FB (l − x) = l (a ≤ x ≤ l )
M M 2 ( x ) = FB (l − x ) = − (l − x ) l
(0 ≤ x < a )
(a < x ≤ l )
第九章梁的内力
(3)作剪力图和弯矩图 M a A C l FS图
bM l
b
B
M FS1 ( x ) = l M FS2 ( x ) = l
M M 1 (x ) = x l
FS1 = − F
M1 + F × a = 0
M 1 = − Fa
1 FS1 截面2—2 F C22 M2 FA 2 F
S2
∑F
y
=0
− FS2 + FA − F = 0
FS 2 = FA − F = 2 F
∑M
o2
=0
M2 + F ×a = 0
M 2 = − Fa
第九章梁的内力
y F 1A2 1 2 FA a
工程力学
第九章梁的内力
第九章梁的内力
§9-1 弯曲变形
梁 ——以弯曲为主要变形的杆件。
第九章梁的内力
最基本最常见的弯曲问题 ——对称弯曲

材料力学教材--内力与内力图

F1 1 kN F2 3 kN
例最大剪力。
L 10 m d 1 m
求图示结构中梁的最大弯矩和
梁中弯矩图呈如图形状，故弯
RA RB
矩极大值出现在 C 截面或 D 截面。
设 C 截面到 A 端距离为，可得 A 端支反力
L L d 1 RA F1 F2 37 4 L L 10 1 M C RA 37 4 2 故有 C 截面弯矩 10
C
YB 14 kN
m
F
0
X C 5 kN
X 0
X B 11 kN
例
画出结构的剪力和弯矩图。
F=5 2 kN/m XXF F
画剪力图
4m 4m
2 kN/m
E XE=8 YF=10 YF Y X XA =11 YEE=4CC=5 C XB B=11 B X =5
YA=4
4m 4m助学习资料
重点与难点
◆ 应透彻理解内力符号规定与外力的区别，尤其应熟练掌握轴力和
弯矩的正负规定。 ◆ 截面法是建立内力方程的最基本的方法，应熟练掌握。注意先将未知内力设正，建立方程时，内力和外力在一起按理论力学的规则进入方程。因此建立内力方程过程中事实上用了两套符号规定。 ◆ 但是在求某个指定截面的内力时，尽量用更简便的方法，不必通过建立内力方程求解。 ◆ 计算梁横截面的内力时，应特别注意外力的方向与其引起的内力符号的关系，以保证内力的正负号正确。 ◆ 正确地计算支座反力是绘制内力图的关键，应确保无误。利用平衡方程求出支反力后，应进行校核。
例
画出结构的内力图。
A
P1 在 BC 段引起剪力和弯矩。
z
L

梁弯矩图梁内力图

常用截面几何与力学特征表表2-5注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）。

基本计算公式如下：⎰•=AdA yI 22．W 称为截面抵抗矩（mm 3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：m axy I W =3．i 称截面回转半径（mm ），其基本计算公式如下：AIi =4．上列各式中，A 为截面面积（mm 2），y 为截面边缘到主轴（形心轴）的距离（mm ），I 为对主轴（形心轴）的惯性矩。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

2．单跨梁的内力及变形表（表2-6~表2-10）（1）简支梁的反力、剪力、弯矩、挠度表2-6（2）悬臂梁的反力、剪力、弯矩和挠度表2-7（3）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8（4）两端固定梁的反力、剪力、弯矩和挠度表2-9（5）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的内力及变形表（1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14）1）二跨等跨梁的内力和挠度系数表2-11注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

[例1] 已知二跨等跨梁l ＝5m ，均布荷载q ＝11.76kN/m ，每跨各有一集中荷载F ＝29.4kN ，求中间支座的最大弯矩和剪力。

梁-弯矩图-梁-内力图--(剪力图与弯矩图)

常用截面几何与力学特征表表2-5授课：XXX授课：XXX授课：XXX授课：XXX授课：XXX授课：XXX授课：XXX注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）。

基本计算公式如下：⎰•=AdA yI 22．W 称为截面抵抗矩（mm 3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：m axy I W =3．i 称截面回转半径（mm ），其基本计算公式如下：AIi =4．上列各式中，A 为截面面积（mm 2），y 为截面边缘到主轴（形心轴）的距离（mm ），I 为对主轴（形心轴）的惯性矩。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

[例1] 已知二跨等跨梁l ＝5m ，均布荷载q ＝11.76kN/m ，每跨各有一集中荷载F ＝29.4kN ，求中间支座的最大弯矩和剪力。

2018年材料力学专题一梁的内力和内力图

材料力学专题一梁的内力和内力图专题一梁的内力和内力图例1求图1(a)所示梁截面 A、C的剪力和弯矩。

解：1）求反力FA=5kN，FB=4kN2）求A左截面的内力，如图(a)所示。

∑Yi=0， Fp+FSA左=0，FSA左=-3kN∑MO=0，Fp⨯2+MA左=0， MA左=-6kN⋅m3）求A右截面的内力，如图(b)所示。

∑Yi=0，-Fp-FSA左+FA=0，FSA左=2kN∑MO=0，Fp⨯2+MA右=0， MA右=-6kN⋅m4）求C左截面的内力，如图(c)所示。

∑Yi=0，FA-FP-q⨯2-FSC左=0，FSC左=0∑MO=0，Fp⨯4-FA⨯2+q⨯2⨯1+MC左=0，MC左==-4kN⋅m5）求C右截面的内力，如图(d)所示。

∑Yi=0，FA-FP-q⨯2-FSC右=0，FSC右=5-3-2=0∑MO=0，Fp⨯4-FA⨯2+q⨯2⨯1+M1+MC右=0，MC右==-6kN⋅m(a)(b)(c)(d) (e)图1【小结】①求指定截面上的内力时，既可取梁的左段为脱离体，也可取右段为脱离体，两者计算结果一致。

一般取外力比较简单的一段进行分析。

②在解题时，通常假设截面上把内力为正，若最后计算结果是正，则表示假设的内力方向（转向）与实际是相同的，否则是相反的。

③该题也可以不画受力图，不写平衡方程而由前面的结论直接求得结果。

例2试计算图2所示各梁指定截面（标有细线者）的剪力与弯矩。

(b) (a)qB图2 图(d) (c)解：(a)取A+截面左段研究，FSA+=F, MA+=0取C截面左段研究，FSC=F, MC=取B-截面左段研究， FSB=F, MB =Fl(b) 求A、B处约束反力如图(d)所示，FA=FB=Me/l取A+截面左段研究，FSA+=-FA=-Me, MA+=Mel取C截面左段研究，MlMFSC=-FA=-e, MA+=Me-FA⨯=el22M取B截面右段研究，FSB=-FB=-e, MB=0l(c) 求A、B处约束反力取A截面右段研究，FSA++BFl 2lqll3l3ql2=q⨯=, MA+=-q⨯⨯=-222482取C-截面右段研究，FSC-=q⨯l=ql, MC-=-q⨯l⨯l=-ql22248lqlllql2取C截面右段研究，FSC+=q⨯=, MC+=-q⨯⨯=-22248-取B截面右段研究，FSB-=0, MB-=0+例3试写出图3所示梁的内力方程，并画出剪力图和弯矩图。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

如有你有帮助，请购买下载，谢谢！
专题一梁的内力和内力图
例1求图1(a)所示梁截面 A 、C 的剪力和弯矩。

解：1）求反力
kN 5=A F ，kN 4=B F
2）求A 左截面的内力，如图(a)所示。

0=∑i Y ， 0=+左SA p F F ，kN 3-=左SA F
0=∑O M ，02=+⨯左A p M F ， m kN 6⋅-=左A M
3）求A 右截面的内力，如图(b)所示。

0=∑i Y ，0=+--A SA p F F F 左，kN 2=左SA F
0=∑O M ，02=+⨯右A p M F ， m kN 6⋅-=右A M
4）求C 左截面的内力，如图(c)所示。

0=∑i Y ，02=-⨯--左SC P A F q F F ，0=左SC F
0=∑O M ，01224=+⨯⨯+⨯-⨯左C A p M q F F ，=左C M m kN 4⋅-=
5）求C 右截面的内力，如图(d)所示。

0=∑i Y ，02=-⨯--右SC P A F q F F ，0235=--=右SC F 0=∑O M ，012241=++⨯⨯+⨯-⨯右C A p M M q F F ，=右C M m kN 6⋅-=
【小结】①求指定截面上的内力时，既可取梁的左段为脱离体，也可取右段为脱离体，两者计算结果一致。

一般取外力比较简单的一段进行分析。

②在解题时，通常假设截面上把内力为正，若最后计算结果是正，则表示假设的内力方向（转向）与实际是相同的，否则是相反的。

③该题也可以不画受力图，不写平衡方程而由前面的结论直接求得结果。

例2试计算图2所示各梁指定截面（标有细线者）的剪力与弯矩。

解：, A F M +==, 2C Fl
M = 取B -SB B M Fl =
(b) 求A 、B 处约束反力
如图(d)所示，l M F F /==
, e A M F M l =-取B 截面右段研究，, 0e
SB B B M F F M l
=-=-= (c) 求A 、B 处约束反力
取A +
截面右段研究，2
33, 22248
SA A l ql l l ql F q M q +
+=⨯==-⨯⨯=-
图1 (d) 图2 (b) (a) q B (c) B
图(d)
如有你有帮助，请购买下载，谢谢！
(a) (b) (c)
图4
取C -截面右段研究，2, 22248
SC C l ql l l ql F q M q --
=⨯==-⨯⨯=-
取C +
截面右段研究，2
, 22248
SC C l ql l l ql F q M q +
+=⨯==-⨯⨯=-
取B -截面右段研究，0, 0SB B F M --==
例3试写出图3所示梁的内力方程，并画出剪力图和弯矩图。

解：(a ) 求支反力
0=∑C M ： 0310126=⨯--⋅Ay F ， kN 7=Ay F
0=∑Y ： 010=-+By Ay F F ， kN 3=By F 列内力方程，
⎩⎨
⎧<<-<<=63
kN 330 kN 7)(S x x x F ， ⎩⎨⎧≤≤≤≤⋅-⋅-=63 30 m kN )6(3m kN 127)(x x x x x M 作剪力图和弯矩图。

(b ) 求支反力
0=∑B M ：02212=⋅+-⋅l
ql ql l F Ay ， F Ay =0 0=∑Y ：0=-⋅-+ql l q F F By Ay ，ql F By 2=
列内力方程
作剪力图和弯矩图。

例4利用内力方程作图4(a)所示简支梁的剪力图和弯矩图。

解：AC 段有：x x q 5)(=
25.210)(x x F S -=，
（0<x <2） 36
510)(x x x M -=，
（0≤x ≤2）
其剪力图和弯矩图如图(b)(c)所示。

由于结构是对称的，荷载也是对称的，
BC 段与AC 段的F S 图是反对称的，M 图是对称的，据此特点可方便地作出AC 段
的剪力图和弯矩图。

例5试用剪力、弯矩与荷载集度之间的微分关系判断图5所示各梁的内力图形态，画出剪力图和弯矩图。

解：(a ) 根据微分关系：()()x F x
x M S d d = 和 ()()q x x M x x F ==22S d d d d AC 段：q 为常数，且0<q ，F S 图从左到右为向下的斜直线，M 图为向上凸的抛物线。

CB 段：q 为常数，且0>q ，F S 图从左到右为向上的斜直线，M 图为向下凹的抛物线。

在C 截面处，F S 图连续，M 图光滑。

(b)
图3
(a)
如有你有帮助，请购买下载，谢谢！
求得几处特殊截面的内力值后即可作出梁的剪力图与弯矩图。

(b ) 求支反力
0=∑A M ： ()022
1322
=⋅⋅-+⋅a q qa a F By
， 3qa F By = 0=∑Y ： 02=⋅-+a q F F By Ay ， 35qa
F Ay = 判断内力图形态并作内力图
AC 段：q 为常数，且q <0，F S 图从左到右为向下的斜直线，M 图为向上凸的抛物线，在
距A 端a 3
5
截面处，M 取极大值。

CB 段：0=q ，F S 图为水平直线，且F S <0，M 图从左到右为向下的斜直线。

在C 截面处，F S 图连续，M 图光滑。

求得几处特殊截面的内力值后即可作出梁的剪力图与弯矩图。

(c) 求支反力
0=∑A M ：()022132=⋅-⋅⋅-⋅a qa a q a F By ， qa F By = 0=∑Y ： 02=-⋅-+qa a q F F By Ay ， qa F Ay 2= 判断内力图形态并作内力图
AC 段：q 为常数，且0<q ，F S 图从左到右为向下的斜直线，M 图为向上凸的抛物线。

C
截面处，有集中力F 作用，F S 图突变，M 图不光滑。

CD 段：q 为常数，且0<q ，F S 图从左到右为向下的斜直线，M 图为向上凸的抛物线。

DB 段：0=q ，Q F 图为水平直线，且F S <0； M 图从左到右为向下的斜直线。

(d)求支反力
0=∑B M ： 0462
1
862=⨯⨯--⋅Ay
F ，kN 33.9=Ay F 0=∑Y ： 046=⨯-+By Ay F F ， kN 67.14=By F 判断内力图形态，作内力图
F S 图：AD 段，0=q ，为水平直线；
DB 段，0<q ，从左到右为向下的斜直线。

M 图：AC 段，0=q ，且F S >0，从左到右为向上的斜直线； C 截面处，有集中力偶e M 作用，有突变；
CD 段，0=q ，且F S >0，从左到右为向上的斜直线，且ab c b //'； DB 段，0<q ，为向上凸的抛物线，且c b '与ce 在c 点相切；
在距D 端m 9
22
截面处，F S =0，M 取极大值17.93kN •m 。

例6试用叠加法画出图6所示梁的弯矩图。

解：(a)
(b)
(a)
(b) (c)
图5 (d)。

材料力学专题一梁的内力和内力图

合集下载