材料力学内力图绘制详细讲解
- 格式:doc
- 大小:210.00 KB
- 文档页数:8



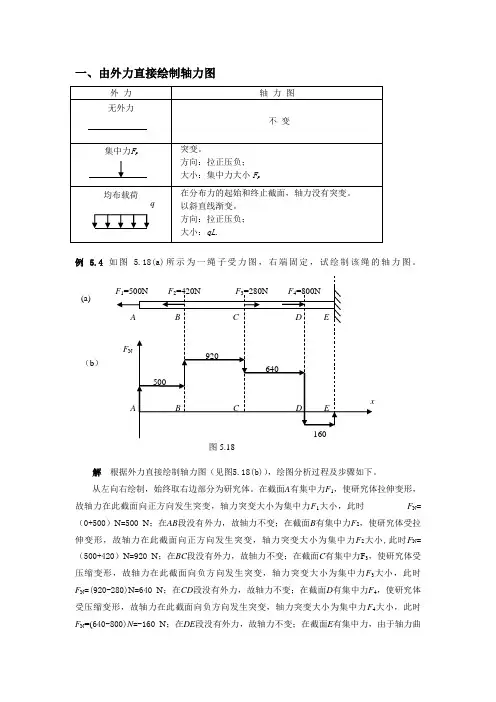
一、由外力直接绘制轴力图例 5.4 如图 5.18(a)所示为一绳子受力图,右端固定,试绘制该绳的轴力图。
解 根据外力直接绘制轴力图(见图5.18(b)),绘图分析过程及步骤如下。
从左向右绘制,始终取右边部分为研究体。
在截面A 有集中力F 1,使研究体拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F 1大小,此时 F N =(0+500)N =500 N ;在AB 段没有外力,故轴力不变;在截面B 有集中力F 2,使研究体受拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F 2大小,此时F N =(500+420)N =920 N ;在BC 段没有外力,故轴力不变;在截面C 有集中力F 3,使研究体受压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F 3大小,此时F N =(920-280)N =640 N ;在CD 段没有外力,故轴力不变;在截面D 有集中力F 4,使研究体受压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F 4大小,此时 F N =(640-800)N =-160 N ;在DE 段没有外力,故轴力不变;在截面E 有集中力,由于轴力曲(b )(a)线与轴线围成封闭图形,故轴力突变为0。
例5.5有一根阶梯轴受力如图5.19(a)所示,试绘制阶梯轴的轴力图。
图5.19解从右向左绘制,始终取左变部分为研究体。
根据外力直接绘制轴力图(见图5.19(b)),绘图分析过程及步骤如下:在截面A有集中力F1,使研究体压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F1大小,此时F N=(0-10)kN=-10 kN;在AB段有均匀分布载荷,使研究体受拉伸变形,故轴力以斜直线规律向正方向渐变,轴力渐变大小为均匀分布载荷大小,此时F N=(-10+10×2)kN=10 kN;在截面B没有力,故此截面轴力没有变化;在BC段没有外力,故轴力不变;在截面C有集中力F2,使研究体受拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F2大小,此时F N=(10+10)kN=20 kN;在CD段没有外力,故轴力不变;在截面D有集中力,由于轴力曲线与轴线围成封闭图形,故轴力突变为0.二、由外力直接绘制扭矩图制其内力图。

材料力学中内力图的直接画法摘要:介绍一种关于材料力学中轴力、扭矩、剪力和弯矩等内力图的直接画法,建立内力的增减与外力方向之间的关系。
关键词:内力图;直接画法;内力;外力。
画内力图是材料力学学习过程中的一个重点,而不少学生在学习这部分内容时感到不好理解,总是不清楚题目要求的截面上的内力应该怎么求。
尤其是弯曲内力中的剪力与弯矩。
为了使同学更好地理解构件的内力、画好内力图,经过摸索与思考,我总结出了关于内力图的一种简单的画法。
本文中约定在各内力图中向上的方向为正向,画图时从左向右画。
希望老师和同学予以指正。
1.轴力、扭矩图轴力图完全可直接根据外力的大小与方向直接画出来。
以水平杆为例,如杆左端有约束,首先求出约束力(外力),向左的外力会引起轴力增加,而向右的外力会引起轴力减小。
例如:图1中所示的杆的A、B、C、D点分别作用有大小为5P、8P、4P、P的力,方向如图1,试画出杆的轴力图。
解:用截面法求OA段内力N1设置截面如图1.X=OV1-P A+P B-P C-P D=0N1-5P+8P-4P-P=0N1=2P同理,求得AB、BC、CD段内力分别为:N2=-3P,N3=5P,N4=P。
轴力图如图1所示。
如果用直接法,只需要求出O截面的约束力R。
由平衡方程R=2P,方向向左,故O截面的轴力从0增加到2P。
OA段无外力,轴力均为2P。
A截面作用有外力PA=5P,方向向右,轴力在该截面将减小5P,即从2P降为-3P。
AB段无外力,轴力均为-3P。
B截面作用有外力8P,方向向左,该截面轴力将增加8P,即从-3P升到5P。
BC段轴力为5P,C截面有外力4P,方向向右,轴力在该截面下降4P。
CD段轴力为P,D截面有外力P,方向向右,该截面轴力下降P,最终为O轴力图终点与x轴重合。
关于扭矩图中扭矩正负的规定,用直接法,将外力偶用右手螺旋法则进行矢量化,矢量沿轴线方向,一水平轴为例,向左的外力偶矩将引起扭矩的增加,向右的外力偶矩将引起扭矩下降,因此在直接法中,扭矩图的画法与轴力图的画法完全一样。
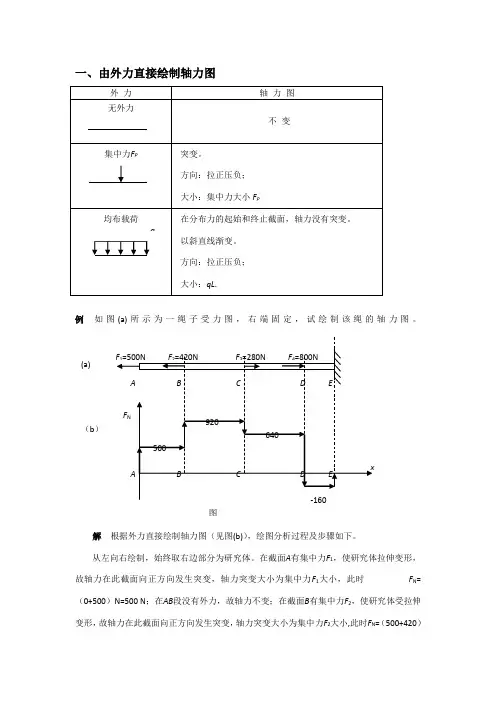
一、由外力直接绘制轴力图例 如图(a)所示为一绳子受力图,右端固定,试绘制该绳的轴力图。
解 根据外力直接绘制轴力图(见图(b)),绘图分析过程及步骤如下。
从左向右绘制,始终取右边部分为研究体。
在截面A 有集中力F 1,使研究体拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F 1大小,此时 F N =(0+500)N=500 N ;在AB 段没有外力,故轴力不变;在截面B 有集中力F 2,使研究体受拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F 2大小,此时F N =(500+420)(b )(a)N=920 N;在BC段没有外力,故轴力不变;在截面C有集中力F3,使研究体受压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F3大小,此时F N=(920-280)N=640 N;在CD段没有外力,故轴力不变;在截面D有集中力F4,使研究体受压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F4大小,此时F N=(640-800)N=-160 N;在DE 段没有外力,故轴力不变;在截面E有集中力,由于轴力曲线与轴线围成封闭图形,故轴力突变为0。
例有一根阶梯轴受力如图(a)所示,试绘制阶梯轴的轴力图。
图解从右向左绘制,始终取左变部分为研究体。
根据外力直接绘制轴力图(见图(b)),绘图分析过程及步骤如下:在截面A有集中力F1,使研究体压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F1大小,此时F N=(0-10)kN=-10 kN;在AB段有均匀分布载荷,使研究体受拉伸变形,故轴力以斜直线规律向正方向渐变,轴力渐变大小为均匀分布载荷大小,此时F N=(-10+10×2)kN=10 kN;在截面B没有力,故此截面轴力没有变化;在BC段没有外力,故轴力不变;在截面C有集中力F2,使研究体受拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F2大小,此时F N=(10+10)kN=20 kN;在CD段没有外力,故轴力不变;在截面D有集中力,由于轴力曲线与轴线围成封闭图形,故轴力突变为0.二、由外力直接绘制扭矩图例如图(a)所示圆轴,左端固定、右端自由,受到三个集中力偶作用,试绘制其内力图。





一、由外力直接绘制轴力图
例 5.4 力图。
解 根据外力直接绘制轴力图(见图5.18(b)),绘图分析过程及步骤如下。
从左向右绘制,始终取右边部分为研究体。
在截面A 有集中力F 1,使研究体拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F 1大小,此时 F N =(0+500)N=500 N ;在AB 段没有外力,故轴力不变;在截面B 有集中力F 2,使研究体受拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F 2大小,此时F N =(500+420)N=920 N ;在BC 段没有外力,故轴力不变;在截面C 有集中力F 3,使研究体受压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F 3大小,此时F N =(920-280)N=640 N ;在CD 段没有外力,故轴力不变;在截面D 有集中力F 4,使研究体受压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F 4大小,此时 F N =(640-800)N =-160 N ;在DE 段没有外力,故轴力不变;在截面E 有集中力,由于轴力曲线与轴线围成封闭图形,故轴力
(b )
(a)
突变为0。
例5.5有一根阶梯轴受力如图5.19(a)所示,试绘制阶梯轴的轴力图。
图5.19
解从右向左绘制,始终取左变部分为研究体。
根据外力直接绘制轴力图(见图5.19(b)),绘图分析过程及步骤如下:
在截面A有集中力F1,使研究体压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F1大小,此时F N=(0-10)kN=-10 kN;在AB段有均匀分布载荷,使研究体受拉伸变形,故轴力以斜直线规律向正方向渐变,轴力渐变大小为均匀分布载荷大小,此时F N=(-10+10×2)kN=10 kN;在截面B没有力,故此截面轴力没有变化;在BC段没有外力,故轴力不变;在截面C有集中力F2,使研究体受拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F2大小,此时F N=(10+10)kN=20 kN;在CD段没有外力,故轴力不变;在截面D有集中力,由于轴力曲线与轴线围成封闭图形,故轴力突变为0.
二、由外力直接绘制扭矩图
外力扭矩图
无外力
不变
集中力F P突变。
方向:右手螺旋法则,四指指向外力偶方向,拇指离开为正;
大小:集中力偶大小F P
均布力偶在分布力的起始和终止截面,扭矩没有突变。
以斜直线渐变。
方向:右手螺旋法则,四指指向外力偶方向,拇指离开为正;
大小:M q
制其力图。
图5.25
解从右向左绘制,始终取左部分为研究体。
根据外力偶直接绘制扭矩图,绘制分析过程及步骤如下:
在截面A有集中力偶M1,变形方向由右手螺旋法则判断,拇指背离截面,故扭矩在此截面向正方向发生突变,扭矩突变大小为集中力偶M1大小,此时m
kN
1
)1
0(•
=
+
=
x
M;在AB 段无外载荷,故扭矩不变;在截面B有集中力偶M2,变形方向由右手螺旋法则判断,拇指指向截面,故扭矩在此截面向负方向发生突变,扭矩突变大小为集中力偶M2大小此时M x=1-2=-1m
kN•;在BC段无外载荷,故扭矩不变;在截面C有集中力偶M3,变形方向由右手螺旋法则判断,拇指背离截面,故扭矩在此截面向正方向发生突变,扭矩突变大小为集中力偶M3大小m
kN
2
)3
1
(•
=
+
-
=
x
M;在CD段有无外载荷,故扭矩不变;在截面D有集中力,由于扭矩曲线与轴线围成封闭图形,故扭矩突变为零。
扭矩图如图5.25(b)所示。
M q
三、由外力直接绘制剪力图和弯矩图
剪力、弯矩与分布载荷间的关系
例5.10如图5.28(a)所示,简支梁AB,在C点承受集中载荷F=6 kN作用,跨度l=3 m,a,试绘制梁的力图。
2
m
解 (1)求支座反力。
取整段梁为研究对象,受力分析如图5.28(b),由平衡条件得
0)(A =∑F M ⇒0B =⋅-⋅a F l F
解得
kN 4B =F
0=∑y F ⇒0B A =-+F F F
解得
kN 2A =F
(2)由外力直接绘制力图。
从A 截面开始,有一向上的集中力F A ,故在此截面剪力向上突变,突变大小等于F A ,弯矩没有变化;AC 段没有外力,故剪力在该段没有变化,由于剪力大于零,故在该段弯矩以斜直线规律向正向变化,从截面A 到截面C 弯矩变化大小为AC 段剪力与x 轴围成的面积即
m kN 4A •=•a F ;在截面C 有一向下的集中载荷F ,故在此截面剪力向下突变F ,弯矩没
有变化;在CB 段没有外力,故剪力在该段没有变化,由剪力小于零,则该段弯矩以斜直线规
律向负向变化,从截面C 到截面B 弯矩变化大小为CB 段剪力与x 轴围成的面积即
m kN 4)(B •=-•a l F 变为0。
例5.11 如图5.29(a)所示外伸梁,试计算其力并画出力图。
图5.29
解 (1)先求支座反力。
取整段梁研究,其受力如图5.29(a),由平衡条件得
∑=-⋅+⋅⇒=020)(2
A B AB q AB F BC F F M
∑=⋅--+⇒=00B A y
AB q F F F F
解得
kN 35,kN 15B A ==F F
(2)由外力直接绘制力图。
从截面A 开始,有一向上的集中力F A ,故在此截面剪力向上突变,突变大小等于F A ,弯矩
没有变化;AB 段有向下的均布力系,故剪力在该段以斜直线规律向下渐渐变化,从截面A 到截面B 剪力值变化q AB ⋅,弯矩以开口向上的抛物线规律渐渐变化,在剪力为零的截面D 弯矩
为极值,从截面A 到截面D 变化值为小三角形面积
m kN 625.52
251515
215•=+⨯
⨯,从截面D 到截面B 变化大三角形面积
m kN 625.152
251525
225•=+⨯
⨯;在截面B 有一向上的集中力F B ,故在该截面剪力向上突变,突变大小等于F B 的大小,弯矩没有变化;BC 段没有外力,故
剪力在该段没有变化,由于剪力大于零,故该段弯矩以斜直线规律向正向变化,从截面C 到截面B 弯矩变化大小为BC 段剪力与x 轴围成的面积。
所绘力图如图5.29(b)、(c)所示。
(3)检查图形是否封闭。
例5.12 如图5.30(a)所示外伸梁,集中力F =10 kN ,均布载荷集度q =10 kN/m ,试利用剪力、弯矩与载荷集度的微分关系绘制出梁的剪力图、弯矩图。
图5.30
解:(1)求A 处约束力。
取整体研究,受力如图5.30(a),建立平衡方程。
0)(A
=∑F M
⇒05.2D =⨯⋅-⋅-⋅BD q AC F AD F
解得
kN 5.17D =F
∑=+⋅--⇒=010D A y
F q F F F
解得
kN 5.2A =F
(2)由外力直接绘制力图。
从截面A 开始,有一向上的集中力F A ,故在此截面剪力向上突变,突变大小等于F A ,弯矩没有变化;AC 段没有外力,故剪力在该段没有变化,由于剪力大于零,则该段弯矩以斜直线规律向正向变化,从截面C 到截面B 弯矩变化大小为AC 段剪力与x 轴围成的面积;截面C 有一向下的集中力F ,故在此截面剪力向下突变,突变大小等于F 的大小,弯矩没有变化;CD 段没有外力,故剪力在该段没有变化,由于剪力小于零,则该段弯矩以斜直线规律向负向变化,从截面C 到截面D 弯矩变化大小为CD 段剪力与x 轴围成的面积; 截面D 有一向上的集中力F D ,故在此截面剪力向上突变F D ,弯矩没有变化;DB 段有向下的均布力系,故剪力在该段以斜直线规律向下渐渐变化,从截面D 到截面B 剪力值变化DB q ⋅,弯矩以开口向上的抛物线规律渐渐变化,在剪力为零的截面D 弯矩为极值,从截面D 到截面B 变化大小为小三角形面积。
(3)检查图形是否封闭。