2012-2013学年高二下学期开学检测数学(理)试题(无答案)

高2014级2012－2013学年度下期2月月考数学（理）一、选择题：本大题共10小题，每小题5分，满分50分. 在每小题给出的四个选项中，只有一项是符合题目要求的.1．某雷达测速区规定：凡车速大于或等于70 km/h 的汽车视为“超速”，并将受到处罚，如图是某路段的一个检测点对200辆汽车的车速进行检测所得结果的频率分布直方图，则从图中可以看出被处罚的汽车大约有( ▲ )．A ．30辆B ．40辆C ．60辆D ．80辆 2．已知直线01)10ax y a x y -=-+-=与直线(平行，则a =( ▲ )（ ）A ．0B ．1C ．21 D ．21-3．已知3(0,)sin ,)254ππααα∈=-且=( ▲ )A ．15B ．15- C ．75D ．75-4．点E 是正四面体ABCD 的棱AD 的中点，则异面直线BE 与AC 所成的角的余弦值为( ▲ )ABCD ．565．设等差数列{}n a 的前n 项和为n S ,若111a =-,376a a +=-,则当n S 取最小值时,n 等于( ▲ ) A ．6 B ．7 C ．8 D ．96．设 A 、B 、C 、D 是空间四个不同的点，在下列命题中，不正确的是( ▲ )A. 若AC 与BD 共面，则AD 与BC 共面B. 若AC 与BD 是异面直线，则AD 与BC 是异面直线C. 若AB=AC,DB=DC,则AD ⊥BCD. 若AB=AC ，DB=DC,则AD=BC7．某单位员工按年龄分为A ，B ，C 三组，其人数之比为5：4：1，现用分层抽样的方法从总体中抽取一个容量为20的样本，已知C 组中甲、乙二人均被抽到的概率是,451则该单位员工总数为( ▲ ) A ．110B ．100C ．90D ．808. 某零件的正（主）视图与侧（左）视图均是如图所示的图形（实线组成半径为2cm 的半圆，虚线是等腰三角形的两腰），俯视图是一个半径为2cm 的圆（包括圆心），则该零件的体积是( ▲ ) A ．4π33cm B ．8π33cm C ．4π 3cm D ．20π33cm第8题图9．阅读右侧的算法框图，输出的结果S 的值为( ▲ ) AB ．C． D ．010．四面体的四个面的面积分别为1S 、2S 、3S 、4S ，记其中最大的面积为S ，则SSi i341∑=的取值范围是( ▲ )A. ]231(, B. ]231[, C.[3432,] D. (3432,] 二、填空题：本大题共5小题，每小题5分，满分25分. 11．圆222430x y x y +-++=的圆心到直线1x y -=的距离为▲ .12. 已知递增的等比数列{}n a 中,28373,2,a a a a +=⋅=则1310a a = ▲ .13. 如图，在正方体1111ABCD A B C D -中，点P 是上底面1111A B C D 内一动点，则三棱锥P ABC -的主视图与左视图的面积的比值为___▲____.14．在△ABC 中，60ABC ∠= ，2AB =，5BC =，在BC 上任取一点D ，使△ABD 为钝角三角形的概率为 ▲ .15．空间三条直线中，任何两条不共面，且两两互相垂直，直线l 与这三条直线所成的角都为α，则αtan = ▲ 。

厦门市2012~2013学年（下）高二质量检测数学试卷（理科）满分150分 考试时间120分钟第Ⅰ卷（选择题 共50分）选择题：本题共10个小题，每小题5分，共50分．在每小题给出的四个选项中，只有一个是符合题目要求的．在答题卷上相应题目的答题区域内作答． 一、1．已知i 为虚数单位，则=+2)1(i i （ ）A ．i 2B ．i 2-C ．2D ．2-2．⎰=30cos πxdx （ ）A ．23-B ．23C ．21D ．13．乘积))()((432132121c c c c b b b a a ++++++展开后共有（ ）A ．9项B ．10项C ．24项D ．32项4．先后抛掷红、蓝两枚骰子，事件:A 红骰子出现3点，事件:B 蓝骰子出现的点数为奇数，则=)/(B A P （ ）A ．61 B ．31 C ．21 D ．365 5．在回归分析中，下列结论错误的是（ ）A ．利用最小二乘法求得的回归直线一定过样本点的中心B ．可用相关指数2R 的值判断模型的拟合效果，2R 越大，模型的拟合效果越好 C ．由测算，某地区女大学生的身高（单位：cm ）预报体重的回归方程是712.85849.0ˆ-=x y，则对于身高为cm 172的女大学生，其体重一定是kg 316.60 D ．可用残差图判断模型的拟合效果，残差点比较均匀的落在水平的带状区域中，说明这样的模型比较合适合适，带状区域的宽度越窄，说明模型的拟合精度越高 6．在nxx )1(2+的二项展开式中，第三项的系数与第二项的系数的差为20，则展开式中含x1的项的系数为（ ）A ．8 B ．28 C ．56 D ．707．已知实数a 在区间)2,0(上等可能随机取值，则函数2332)(ax x x f -=在区间)1,0(上有极小值的的概率是（ ）A ．21 B ．31 C ．41 D ．51 8．某电视台连续播放6个广告，分别是三个不同的商业广告和三个不同的公益广告，要求最后播放的不能是商业广告，且任意两个公益广告不能连续播放，则不同的播放方式有（ ）A ．36种 B ．108种 C ．144种 D ．720种9．某高二学生在参加历史、地理反向会考中，两门科目考试成绩互不影响，记X 为“该学生取得优秀的科目数”，其分布列如下表所示，则)(x D 的最大值是（ ）X0 1 2Pab21 A ．21 B ．23 C ．45D ．1 10．已知函数)(x f 的定义域为]6,2[-，x 与)(x f 部分对应值如下表，)(x f 的导函数)(x f y '=的图象如图所示．给出下列说法： x2-56 )(x f32- 2-3①函数)(x f 在)3,0(上是增函数；②曲线)(x f y =在4=x 处的切线可能与y 轴垂直； ③如果当],2[t x -∈时，)(x f 的最小值是2-，那么t 的最大值为5；④]6,2[,21-∈∀x x ，都有a x f x f ≤-|)()(|21恒成立，则实数a 的最小值是5． 正确的个数是（ ）A ．0个 B ．1个 C ．2个 D ．3个第Ⅱ卷（非选择题 共100分）二、填空题：本大题共6小题，每小题4分，共24分．在答题卷上的相应题目的答题区域内作答．11．7722107)21(x a x a x a a x +⋅⋅⋅+++=-，则=+⋅⋅⋅+++7321a a a a12．如图，在复平面内，复数21,z z 对应的向量分别是OB OA ,，则复数21z z -的共轭复数是13．已知),4(~2σξN ，且7.0)62(=<<ξP ，则=<)1(ξP14．从1，3，5，7，9这五个数中，每次取出两个不同的数分别记为b a ,，则斜率不同的直线03=++by ax 共有 条15．已知函数xe x x xf )22()(2--=，方程m x f =)(有三个解，则实数m 的取值范围是 16．研究问题：“已知关于x 的不等式02>+-c bx ax 的解集为)2,1(，解关于x 的不等式02>+-a bx cx ”，有如下解法： 解：由0)1()1(022>+-⇒>+-xc x b a c bx ax ，令x t 1=，则)1,21(∈t ， 所以不等式02>+-a bx cx 的解集为)1,21(参考上述的解法，已知关于x 的不等式0log log log 222<++++cx bx a x m 的解集为)22,21(，则关于x 的不等式01log 1log 1log log 2222<--+-x c x b x a x m 的解集为 三、解答题：本大题共6小题，共76分．解答题应写出文字说明，证明过程或演算步骤，在答题卷上相应题目的答题区域内作答． 17．（本小题满分12分）已知函数bx x a x x f +-+=23)1()(，)(x f 在1=x 处的切线斜率为9-，且)(x f 的导函数)(x f '为偶函数． （Ⅰ）求b a ,的值；（Ⅱ）求)(x f 的极值．18．（本小题满分12分）为了检测某种研制出的禽流感疫苗对家禽的免疫效果，某研究中心随机抽取了50只鸡作为样本，进行家禽免疫效果试验，得到如下缺少部分数据的22⨯列联表．已知用分层抽样的方法，从对禽流感病毒没有免疫力的20只鸡中抽取8只，恰好抽到2只注射了该疫苗的鸡．（Ⅰ）从抽取到的这8只鸡随机抽取3只进行解剖研究，求至少抽到1只注射了该疫苗的鸡的概率；（Ⅱ）完成下面22⨯列联表，并帮助该研究和纵向判断：在犯错误的概率不超过%5.0的前提下，能否认为这种新研制出的禽流感疫苗对家禽具有免疫效果？有免疫力 没有免疫力总计 有注射疫苗 20 没有注射疫苗总计205019．（本小题满分12分）厦门某鱼苗养殖户，由于受养殖技术水平和环境等因素的制约，会出现一些鱼苗的死亡，根据以往经验，鱼苗的死亡数p （万条）与月养殖数x （万条）之间满足关系：2,(14)6325,(4)12x x P x x x ⎧≤≤⎪⎪=⎨⎪+-≥⎪⎩，已知每成活1万条鱼苗可以盈利2万元，但每死亡1万条鱼苗将亏损1万元．（Ⅰ）试讲该养殖户每月养殖鱼苗所获得的利润T （万元）表示为月养殖量x （万条）的函数；（Ⅱ）该养殖户鱼苗的月养殖量是多少时获得的利润最大，最大利润是多少？（利润=盈利—亏损）20．（本小题满分12分）已知),,3,2,1(0n i x i ⋅⋅⋅=>，我们知道有4)11)((2121≥++x x x x 成立．（Ⅰ）请证明9)111)((321321≥++++x x x x x x ； （Ⅱ）同理我们也可以证明处16)1111)((43214321≥++++++x x x x x x x x ．由上述几个不等式，请你猜测与n x x x +⋅⋅⋅++21和),2(111*21N n n x x x n∈≥+⋅⋅⋅++有关的不等式，并用数学归纳法证明．21．（本小题满分14分）某学校举办趣味运动会，甲、乙两名同学报名参加比赛，没人投篮2次，每次等可能选择投2分球或3分球．据赛前训练统计：甲同学投2分球命中率为53，投3分球命中率为103；乙同学投2分球命中率为21，投3分球命中率为52，且每次投篮命中与否相互之间没有影响．（Ⅰ）若甲同学两次都选择投3分球，求其总得分ξ的分布列和数学期望；（Ⅱ）记“甲、乙两人总得分之和不小于10分”为事件A ，记“甲同学总得分大于乙同学总得分”为事件B ，求)(AB P ．22．（本小题满分14分）已知函数x ax g ae x f xln 1)(,)(==，其中0>a ，若函数)(x f 和)(x g 在它们图象与坐标轴交点处的切线互相平行．（Ⅰ）求这两平行切线间的距离；（Ⅱ）若对于任意1)(,+≥∈mx x f R x （其中0>m ）恒成立，求m 的取值范围； （Ⅲ）当),0(0+∞∈x ，把|)()(|00x g x f -的值称为函数)(x f 和)(x g 在0x 处的纵差，求证：函数)(x f 和)(x g 所有纵差都大于2。

四川省成都七中2012-2013学年高二下学期入学考试（数学理）————————————————————————————————作者：————————————————————————————————日期：318212921625267454DCAA 1C 1B 1成都七中2012-2013学年高二下学期入学考试数学（理）试题一、选择题(每小题5分,共75分,在每小题给出的四个选项中,只有一项是符合要求的.) 1.已知221,n nC -=则n =( )(A)5 (B)6 (C)7 (D)8 2.从0,2,3,4,6,12六个数中任取两个不同数作积,则不同的积有( )个.(A)7 (B)9 (C)11 (D)153.已知椭圆的方程为22195x y +=,则此椭圆的离心率为( )(A)23 (B)53 (C)49 (D)594.某校高二年级15个班参加成都市调研考试的参考人数的茎叶图 如图,则这组数据的中位数和众数分别是( ) (A)51和51 (B)51和52 (C)52和51 (D)52和525.在四面体ABCD 中,,E F 分别是,AB CD 的中点,若AC BD ⊥,且4,3,AC BD ==则 EF =( )(A)5 (B)4 (C)3 (D)2.56.双曲线221412x y -=的一个焦点坐标是( )(A)(0,8) (B)(22,0)-(C)(0,23) (D)(4,0)- 7.右侧的程序执行后的结果是( )(A)910(B)9 (C)10 (D)1098.在面积为S 的ABC ∆内部任取一点P ,则PBC ∆的面积大于34S 的概率是( ) (A)116(B)14(C)34(D)9169.352()x x-展开式中的常数项为( ) (A)40- (B)40 (C)10- (D)1010.如图,在直三棱柱111ABC A B C -中,11,,2AB AC AB AC AA ⊥==D 是1AA 的中点,则1BC与平面BCD 所成的角正弦值为( ) (A)73 (B)147S=0 i=1DOS=S+1/(SQR(i )+SQR(i +1)) i=i+1 LOOP UNTILi>99PRINT S END(C)142 (D)2311.五个不同的元素(1,2,3,4,5)i a i =排成一列,规定1a 不许排第一,2a 不许排第二,则不同的排法种数为( )(A)48 (B)78 (C)96 (D)108 12.四边形ABCD 是正方形,MD ⊥平面ABCD ,NB ⊥平面ABCD ,且.MD NB AB == 则二面角A MN C --的余弦值为( )(A)63 (B)63- (C)13 (D)13-13.欢乐斗地主是一款QQ 游戏,其规则：两名农民为一方合作对战一名地主,使用一副共54张的扑克牌,每人17张牌,剩余的3张归地主,只要有一人出完手中的牌,则此盘游戏结束.地主最先出完牌,则地主一方赢；两农民中的任何一人最先出完牌,则农民一方赢.输赢用欢乐豆结算： (1)欢乐豆不足2000的人不能当地主.(2)若农民一方赢,则两农民都赢地主1000欢乐豆.若地主一方赢,则两农民都输1000欢乐豆给地主(欢乐豆不足1000的农民,则把所有欢乐豆都输给地主).甲乙丙三人玩欢乐斗地主,已知甲当地主时,最先出完牌的概率为1,2甲当农民时(不管谁当地主)最先出完牌的概率都为730；乙当地主时,最先出完牌的概率为13,30乙当农民时(不管谁当地主)最先出完牌的概率为16.现正进行的一盘游戏,甲丙的欢乐豆都不少于2000,乙的欢乐豆只有500,在甲乙丙三人斗地主的技术和牌运都不发生变化的前提下,抢不抢地主当?甲丙如何选择?( )(A)甲不抢地主当丙抢地主当 (B)甲抢地主当丙不抢地主当 (C)甲丙都抢地主当 (D)甲丙都不抢地主当,结束游戏14.设点1F 是椭圆221123x y +=的左焦点,弦AB 过椭圆的右焦点,则1F AB ∆的面积的最大值是( )(A)6 (B)12 (C)33 (D)6315.已知[0,10](1,2,,10),i x i ∈=L 1210,,,x x x L 的平均数为7.5,当2212(10)(10)x x -+-++L210(10)x -取得最大值时,1210,,,x x x L 这十个数中等于0的数的个数为( )(A)0 (B)1 (C)2 (D)3424ABCD成都七中2012-2013学年下期2014级入学考试数学试卷(理科)答题卷考试时间：120分钟 总分：150分命题人：巢中俊 审题人：张世永二、填空题(每小题5分,共30分.把答案填在题中横线上.)16.乘积126127125()()()a a a b b b c c c +++++++++L L L 展开后,共有 项. 17.在正四面体ABCD (各棱都相等)中,E 是BC 的中点,则异面直线AE 与CD 所成的角的余弦 值为18.已知椭圆224ax y +=与221129x y +=的焦距相等,则a = 19.将一张面值1元的人民币全部换成面值1角,2角和5角的硬币,则换法总数为 20.某项测试成绩满分10分,随机抽取若干名学生参加测试,得分统计如图所示,则得分的平均数为x =(第20题图) (第21题图)21.如图,在四边形ABCD 中,90,30,DAB ADC ∠=︒∠=︒4, 2.AB AD CD === 将四边形ABCD 绕AD 旋转一周,则所成几何体的体积为(台体的体积公式11221()3V S S S S h =++)三、解答题(每小题15分,共45分.解答应写出文字说明、证明过程或演算步骤.)22. (1)以正方体的顶点为顶点,可以确定多少个四棱锥?(2)黑暗中从3双尺码不同的鞋子中任意摸出3只,求摸出3只中有配成一双(事件A )的概率.(3)利用二项式定理求2013143被12除所得的余数.23.已知Rt ABC ∆中,90,4,2,ABC AB BC ∠=︒==,,D E 分别是,AB AC 的中点,将ADE ∆沿着DE 翻折成1,A DE ∆使得平面1A DE ⊥平面DECB ,F 是1A B 上一点且1A E ∥平面C A 1D E DABBE C FFDC .(1)求1A F FB.(2)求三棱锥1D ACF -的体积. (3)求1A B 与平面FDC 所成角的大小.24.已知圆221:4,C x y +=圆222:25.C x y +=点O 为坐标原点,点M 是圆2C 上的一动点,线段OM 交圆1C 于,N 过点M 作x 轴的垂线交x 轴于0M ,过点N 作0M M 的垂线交0M M 于.P(1)当动点M 在圆2C 上运动时,求点P 的轨迹C 的方程.P N M 0OMxy(2)设直线:5xl y m =+与轨迹C 交于不同的两点,求实数m 的取值范围. (3)当55m =时,直线l 与轨迹C 相交于,A B 两点, 求OAB ∆的面积.成都七中2012-2013学年下期2014级入学考试数学试卷(理科)试卷参考答案一、选择题(每小题5分,共75分,在每小题给出的四个选项中,只有一项是符合要求的.)14.设直线AB的方程为3x my=+,联立2211233x yx my⎧+=⎪⎨⎪=+⎩消x得22(4)630m y my++-=.设1122(,),(,)A x yB x y.则12122263,44my y y ym m+=-=-++.122121212121221133()4123.24F ABmS F F y y y y y y y ym ∆+ =-=-=+-=⋅+令21,t m=+则 1.t≥12123123123 6.3323F ABtSt tt∆=⋅=≤=++(3t=时等号成立)二、填空题(每小题5分,共30分.把答案填在题中横线上.)16. 210 17.3618.447或19. 10 20. 6 21.203(28)3π-三、解答题(每小题15分,共45分.解答应写出文字说明、证明过程或演算步骤.)22.解(1)141248.C=…………5分CA 1D BE xyz FOOCA 1DEDABBECF(2)1134363()5C C P A C ==. …………10分 (3)2013201322013143(1441)(121)=-=- …………12分02201312201212012212012201320132013201320132013(12)(12)(1)(12)(1)(1)C C C C =+-++-+-L20132013201312(1)M C =+-(M 是整数) …………14分 12112(1)11.M M =-=-+所以2013143被12除所得的余数为11. …………15分23.解(1)连接EB 交DC 于,O 连接.FO11111.A E FDC A E BA E A E FO FDC BA E FO ⎫⎪⊂⇒⎬⎪=⎭I 平面平面平面平面∥∥ …………3分 ,D E 分别是,AB AC 的中点12DE BC ODE OCBDE BC ⇒∆∆⎧⎪⇒⇒⎨=⎪⎩∥∽12EO DE OB CB ==. 所以在1BA E ∆中,11.2A F EO FB OB == …………5分(2) 1111 . A DE DECB A DE DECB DE A D DECB A D DE ⊥⎫⎪=⇒⊥⎬⎪⊥⎭I 平面平面平面平面平面11111133D A CF C A DF C A DB A DCB V V V V ----===11224(2).3329⨯=⨯⨯⨯= …………10分(3)1.A D DECB ⊥平面又.DE DB ⊥以1,,DE DB DA u u u r u u u r u u u u r 为正交基底建立如图所示的空间直角坐标系.D xyz - 则1(0,0,0),(0,0,2),(0,2,0),(2,2,0).D A B C …………7分设(,,).F x y z 因为11.2A F FB =所以11,2A F FB =u u u u r u u u r 即1(,,2)(,2,),2x y z x y z -=---所以24(0,,).33F24(2,2,0),(0,,).33DC DF ==u u u r u u u r 设平面FDC 的法向量000(,,).n x y z =r则000000200x y n DC y z n DF ⎧+=⋅=⎧⎪⇒⎨⎨+=⋅=⎩⎪⎩u u u r r u u u r r ,令01,z =则(2,2,1).n =-r 又1(0,2,2)A B =-u u u r .设1A B 与平面FDC 所成角的大小为θ,则1112sin cos ,.2A B n A B n A B nθ⋅=〈〉==u u u r r u u u r r u u u r r 因为[0,],2πθ∈所以1A B 与平面FDC 所成角的大小4π. …………15分 24.解(1)设点(,)P x y .则(,),(,)M N M x y N x y .从而(,),(,)M N OM x y ON x y ==u u u u r u u u r因为52OM ON =u u u u r u u u r ,所以5(,)(,)2M N x y x y =.即55,.22N M x x y y ==所以5(,)2M x y . 点M 在圆2C 上,所以225()252x y +=.整理得点P 的轨迹C 的方程：22 1.254x y += …………5分(2)联立221.254 5x y x y m ⎧+=⎪⎪⎨⎪=+⎪⎩消y 得到2225200x mx m ++-=. …………7分因为直线:5x l y m =+与轨迹C 交于不同的两点,所以22(2)4(520)0,m m ∆=--> 即2 5.m <所以实数m 的取值范围为(5,5).- …………10分(3)(方法1)直线5:.55x l y =+设1122(,),(,)A x y B x y , 联立221.2545 55x y x y ⎧+=⎪⎪⎨⎪=+⎪⎩消x 得到2251905x x +-=.则121225,19.5x x x x +=-=- 22221212121255()()()[()()]5555x x AB x x y y x x =-+-=-++-+ 2212121226262686()()4.5555x x x x x x =-=+-=⨯ 直线:550.l x y -+=设O 到直线AB 的距离为,d 则d =205055.2615-⨯+=+ 112686546.2255526OAB S AB d ∆==⨯⨯⨯= …………15分。

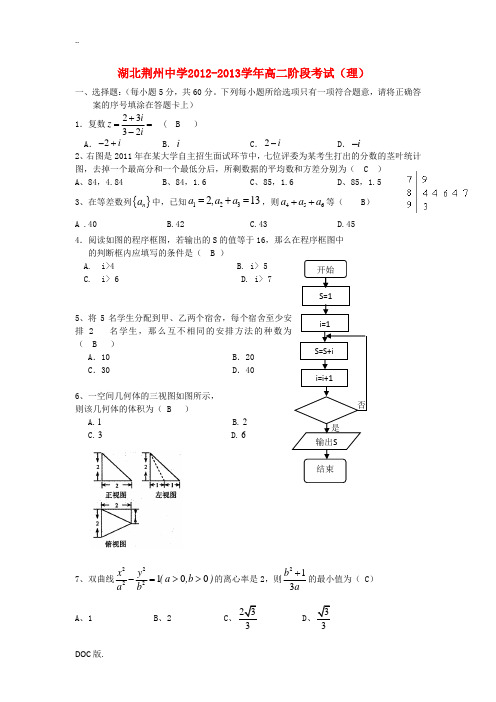
开始S=1i=1输出S结束i=i+1S=S+i是否湖北荆州中学2012-2013学年高二阶段考试（理）一、选择题：（每小题5分，共60分。

下列每小题所给选项只有一项符合题意，请将正确答案的序号填涂在答题卡上） 1．复数2332iz i+==- ( B ） A ．2i -+ B ．i C ．2i - D ．i - 2、右图是2011年在某大学自主招生面试环节中，七位评委为某考生打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为（ C ） A 、84，4.84 B 、84，1.6 C 、85，1.6 D 、85，1.5 3、在等差数列{}n a 中，已知1232,13a a a =+=，则456a a a ++等（ B ）A .40 B.42 C.43 D.45 4．阅读如图的程序框图，若输出的S 的值等于16，那么在程序框图中 的判断框内应填写的条件是（B ）A. i>4B. i> 5C. i> 6D. i> 75、将5名学生分配到甲、乙两个宿舍，每个宿舍至少安排 2 名学生，那么互不相同的安排方法的种数为（ B ）A ．10B ．20C ．30D ．406、一空间几何体的三视图如图所示，则该几何体的体积为（ B ）A.1B.2C.3D.67、双曲线2222100x y (a ,b )a b -=>>的离心率是2，则213b a+的最小值为（ C ）A 、1B 、2C 、233 D 、338、曲线||||ln x x x y =的切线的斜率的取值范围是（ B ） A. (- ∞, 0) B. (0 , + ∞) C.(- ∞,+∞) D.( 0,1 )9、在区间[－1，1]上任取两数s 和t ，则关于x 的方程20xsx t 的两根都是正数的概率为（ A ）A 、148B 、124C 、112 D 、4110、已知()()()()10210012101111x a a x a x a x +=+-+-++-…，则8a = (B) A. 180-B. 180C. 45D. 45-11、已知定义在R 上的函数)(x f y =满足 )()2(x f x f =+，当 11≤-x 时，3)(x x f = 则函数 ||log )(51x x f y +=的零点的个数（ D ）A. 3B. 4C. 5D. 6 12.已知点P 在曲线y=ex(e 自然对数的底数)上，点Q 在曲线y=lnx 上， 则丨PQ 丨的最小值是 (A )A. B. 2e C. D. e二、填空题（本大题共4小题,每小题5分,共20分）13、设变量x 、y 满足约束条件则的最大值为____5___. 14、设函数()(0)2xf x x x =>+,观察: 1()(),2xf x f x x ==+21()(()),34xf x f f x x ==+32()(()),78xf x f f x x ==+43()(()),1516xf x f f x x ==+根据以上事实，由归纳推理可得：当n N +∈且2n ≥时，1()(())n n f x f f x -== .答案：()(21)2n n nxf x x =-+ 15. 化简：()sin 40tan103︒︒-= 1- .16.已知函数()f x 的定义域为[-1,5], 部分对应值如下表，()f x 的导函数/()y f x =的图像如图所示。

“华安、连城、永安、漳平一中,龙海二中,泉港一中”六校联考2012-2013学年下学期第二次月考高二数学（理科）试题 （考试时间：120分钟 总分：150分）参考数据和公式 2×2列联表2K 公式:22()()()()()n ad bc K a b c d a c b d -=++++，2K 的临界值表：1221ni ii nii x y nx yb xnx==-=-∑∑，a y bx =-,残差和公式为)ˆ(1i ni iyy-∑= ★友情提示：要把所有答案都写在答题卷上，写在试卷上的答案无效.一、选择题（本题共10个小题,每小题5分，共50分。

在每小题给出的四个选项中,只有一项是符合题目要求的。

）1．函数2()f x x =在3x =处的导数等于A ．3B ．4C ．6D ．9 2．已知i 为虚数单位，)21(i i Z +⋅=，则复数Z 对应的点位于A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．已知随机变量X ～(,0.8)B n ,6.1)(=X D ，则n 的值是A ．8B ．10C ．12D ．144．用三段论推理命题：“任何实数的平方大于0,因为a 是实数，所以2a ＞0"，你认为这个推理A ．大前题错误B ．小前题错误C ．推理形式错误D ．是正确的5．从黄瓜、白菜、油菜、扁豆4个蔬菜品种中选出3种，分别种在不同土质的三块土地上，其中黄瓜必须种植，则不同的种植方法种数为 ks5uA ．6种B ．12种C ．18种D ．24种 6。

某次市教学质量检测,甲、乙、丙三科考试成绩的直方图如图所示（由于人数众多,成绩分布的直方图可视为正态分布），则由图中曲线可得下列说法中正确的一个是A. 甲科总体的标准差最小B. 乙科总体的标准差及平均数都居中C. 丙科总体的平均数最小D. 甲、乙、丙的总体的平均数不相同7．抛掷一颗骰子两次，定义随机变量⎪⎩⎪⎨⎧=次的点数）次的点数等于第第次的点数）次的点数不等于第第21(121(0X ，随机变量X 的方差=)(X DＡ．61 Ｂ．185 Ｃ．365 Ｄ．658．三位数中，如果十位上的数字比百位上的数字和个位上的数字都大，则称这个数为凸数，如254, 674等都是凸数，那么，各个数位上无重复数字的三位凸数有Ａ．120个 Ｂ．204个 Ｃ．240个 Ｄ．360个9．()1nax by -+展开式中不含x 的项的系数 绝对值的和为243,不含y 的项的系数绝对值的和为32，则,,a b n 的值可能为A ．2,1,5a b n ==-=B ．1,2,5a b n =-==C ．1,2,6a b n =-==D ．2,1,6a b n =-=-=10．定义在区间[0,a ］上的函数（x ）的图像如右图所示，记以A(0，（0)）,B(a ，)(a f ），C （x ，（x))为顶点的三角形面积为S(x)，则函数S(x ）的导函数S ′ （x ）的图像大致是二、填空题(本题共5小题,每小题4分,共20分）11. 复数21(1)i i++的值是 *＊＊*** ．12。

三明市2012—2013学年第二学期普通高中阶段性考试高二理科数学试题（考试时间：2013年7月 日上午8：30—10：30 满分：150分）一、选择题（本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一个选项符合题目要求，请把答案填在答题卷相应的位置上）1．集合{i ,N 5}n x x n n *=∈≤且（其中i 是虚数单位）中元素的个数是A ．1B ．2C ． 4D ．52．已知曲线C 的参数方程为2cos (2sin x y θθθ=⎧⎨=⎩，为参数），则下列各点不在曲线C 上的坐标是A ．） B．C ．D ．1,1（　） 3．用反证法证明命题“a b ∈N ，，如果ab 为偶数，那么a ，b 中至少有一个为偶数”，则正确的假设内容是A ．a ,b 都为偶数B ．ab 不为偶数C ．a ,b 都不为偶数D ．a ,b 中有一个不为偶数4．标准正态总体(0,1)N 在正态总体的研究中占有非常重要的地位，如图是标准正态曲线，已知0)0.3Pa x <<=（-， 则)P x a >（等于 A ．0.2 B ．0.3 C ．0.7D.15．在复平面上点P 对应的复数1i z =-+（其中i 是虚数单位），以原点为极点，实轴正半轴为极轴建立极坐标系，则点P 的极坐标是 A ．(1,)4πB ．3)4πC ．)4πD. 3(1,)4π6．下面是一个22⨯列联表：则表中a 、b A ．94、96 B ．52、54 C ．52、50 D ．54、527．在二项式101()x x-的展开式中，系数最大的项是（ ）A ．第5项B ．第6项C ． 第7项 D. 第5项和第7项８．设凸n 边形的对角线条数为(f n ），若凸1n +边形的对角线条数(+1=(+f n f n m ）），则m 的表达式为A ．1n +B ．nC ． 1n - D. 2n -9．从高二年段4个文科班和5个理科班中任意选出3个班级参加学校活动，若选出的班级至少有一个文科班和一个理科班，则不同的选法种数为 A ．70B ．84C ． 140D. 42010．夏令营组织25名营员去游览宁化天鹅洞、将乐玉华洞、泰宁大金湖三个景点,规定每人必须去一处,最多去两处游览．在所有可能的游览方案中,设游览景点完全相同的人数为m 人,则m 的最小值是 A.8 B. 7 C. 6 D. 5二、填空题（本大题共5小题中，每小题4分，共20分.请把答案写在答题卷相应位置上）11．在三段论中,若大前提为：无限不循环小数是无理数；小前提为：3是无限不循环小数；则结论为: ☆☆☆.12．曲线C 经过伸缩变换5,3x x y y '=⎧⎨'=⎩后得到曲线Γ：221259x y ''+=，则曲线C 的方程为☆☆☆. 13．从装有3个红球和2个白球的袋子中不放回地依次摸出两个球，则在第一次摸到红球的条件下，第二次仍然摸到红球的概率☆☆☆.14．某商场用以往的统计数据得到A 、B 两种方案的盈利表，经计算它们的均值都是50万元，根据经验，商场盈利越稳定，对商场越有利.请结合下表中的数据进行决策，该商场应选择的方案是☆☆☆. (填A 方案或B 方案)自然状况AB1S0.20 55 56 2S 0.30 45 51 3S0.50514715．高二数学研究性学习小组在研究+2+4k k k m m mC C C 、、(,)m k k m **∈∈≤N N 且是否具有某种关系时,按如下规律进行取值：第一组：2412121C C C ６２ 第二组：681022121C C C １ 第三组：111315323232C C C 第四组：171921454545C C C ……请你猜测第n 组的第三个数rp C 中r 的表达式为☆☆☆.（结果用含n 的式子表示）三、解答题（本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤） 16．（本小题满分13分）已知复数12=1i ,2i z z b =－＋（其中i 是虚数单位，R b ∈）. （Ⅰ）若21z z ⋅为纯虚数,求b 的值；（Ⅱ）若21z z 在复平面上对应点的横坐标为1,求21||zz 的值.17．（本小题满分13分）在直角坐标系xOy 中，直线l的参数方程为1,2x y ⎧=-⎪⎪⎨⎪=+⎪⎩ (t 为参数)；在极坐标系中(与直角坐标系xOy 取相同的长度单位，且以原点O 为极点，以x 轴正半轴为极轴)，抛物线C 的极坐标方程为2cos sin ρθθ=．（Ⅰ）将抛物线C 的极坐标方程化为直角坐标方程；（Ⅱ）若直线l 与抛物线C 相交于A ，B 两点，求线段AB 的长．18．（本小题满分13分）从某大学中随机选取8名女大学生,其身高和体重数据如下表所示.已知8名女大学生的平均身高为165cm ,平均体重为55kg . （Ⅰ）求345x x x ++及4y 的值；（Ⅱ）若选取身高为自变量x ，根据女大学生的身高预报体重的线性回归方程为0.8y x a =+（a 为实数）,请你预报一名身高为168cm 的女大学生的体重.19．（本小题满分13分）已知230123(12)n n n x a a x a x a x a x -=+++++．（Ⅰ）若1121n n C -+=,求3a 的值； （Ⅱ）若100123(1)3n n a a a a a -+-++-=,求012135(21)(21)n nn n n n nS C C C n C n C -=+++⋅⋅⋅+-++的值．20．（本小题满分14分）学校组织甲、乙、丙、丁4名学生到A 、B 、C 三个工厂进行社会实践活动，每个学生只能去一个工厂.（Ⅰ）问有多少种不同分配方案？（Ⅱ）若每个工厂都有学生去，求学生甲到A 工厂进行社会实践活动的概率；（Ⅲ）若每个学生选择A 工厂的概率都是13，记ξ为选择A 工厂的学生人数，求ξ的分布列及数学期望.21．（本小题满分14分）以下是求2222123(N )n n *++++∈的一种方法． 先求和1223++(1)n n ⨯+⨯+，可以通过：[]1(1)(1(2(1(13k k k k k k k k +=++-+））-）），得到以下n 个裂项式：(123012),⨯⨯⨯-⨯⨯112=3(234123),⨯⨯⨯-⨯⨯123=34(345234),⨯⨯⨯-⨯⨯13=3……()()()()1(1)1211,3n n n n n n n n ⨯+=⎡++--+⎤⎣⎦ 将上述n 个裂项式累加得到：()()1122311(2)3n n n n n ⨯+⨯+++=++，再根据2(1)k k k k +=+，得到22221(11)(22)(33)()(1)(2)3n n n n n ++++++++=++，即()22221123123(1)(2)3n n n n n +++++++++=++，从而求得22221123(1)(21).6n n n n ++++=++(Ⅰ)请你写出123⨯⨯，234⨯⨯及()()12n n n ++的裂项式；(Ⅱ)设正项数列{}n a 的前n 项和为n S ，且23333123n S n =++++，类比上述方法，求n S 的表达式；(Ⅲ)在(Ⅱ)的条件下，设211(1)(1)n n nb m a a =---，若1n n b b +>对任意n *∈N 恒成立，求实数m 的取值范围．三明市2012—2013学年第二学期普通高中阶段性考试高二理科数学试题参考答案与评分标准一、选择题：二、填空题：1112．221x y += 13．12 14．B 方案 15．2562n n ++三、解答题：16．解：（Ⅰ）12z z ⋅＝(1i)(2i)b -+＝(2)(2)i b b ++-，…………………………………4分因为21z z ⋅为纯虚数，所以2＋b ＝0且b －2≠0，则b ＝－2． ……………………6分 （Ⅱ）12z z ＝2i 1i b +-＝22i 22b b-++， ………………………………………9分 因为12z z 在复平面上对应点的横坐标为1, 所以22b-＝1，则b ＝0， ………………………………………11分 因此12z z ＝1＋i ，所以21zz． ………………………………………13分17．解：（Ⅰ）由2cos sin ρθθ=，得22cos sin ρθρθ=，即y ＝x 2，则抛物线C 的直角坐标方程为y ＝x 2. ………………………………………4分（Ⅱ）将直线l的参数方程1,2,x y ⎧=--⎪⎪⎨⎪=+⎪⎩代入抛物线C的方程，得2＝2(1)-.整理得220t -=，则12122t t t t +==-， …………………………………9分 所以|AB |＝12||t t -AB. ………13分 18．解：（Ⅰ）因为8名女大学生的平均身高为165cm ,所以345x x x ++=8⨯165-（3⨯165+155+170），即345x x x ++=500． ………………3分 因为女大学生的平均体重为55kg ，所以－7＋2－5＋(4y －55)＋9＋6－8＋4＝0，解得4y ＝54. ……………………6分 （Ⅱ）因为女大学生的平均身高为165cm ,平均体重为55kg .由回归方程0.8y x a =+（a 为实数），得550.8165a =⨯+，解得a ＝－77，………10分 所以线性回归方程为0.877y x =-，当168x =时，57.4y =．即对于女大学生的身高为168cm 时，由回归方程可预报其体重大约为57.4kg ．……13分19. 解：（Ⅰ）因为1211n n n C C -++=＝(1)2n n +＝21，所以2420n n +-=，解得n ＝6，n ＝－7（舍去）， 则n ＝6，所以333461(2)T C x =⋅⋅-＝380x -，因此380a =-. ………………………5分（Ⅱ）令1x =- ，则1033n =，所以10n =， ………………………7分因为012135(21)(21)n nn n n n nS C C C n C n C -=+++⋅⋅⋅+-++， 由组合数性质得0121(21)(21)(23)3n n n n n n n S n C n C n C C C -=++-+-+⋅⋅⋅++，……………10分 相加得2S ＝0121(22)()n nn n n n n n C C C C C -++++++＝(22)2n n +⋅，因此S ＝(1)2n n +⋅. ………………………12分 当n ＝10时，S ＝11×210＝11264. ……………………13分 20. 解：（Ⅰ）34＝81种， ………………………………………3分（Ⅱ）223323234313C A A P C A +==， ……………………………………6分 （Ⅲ）依题意，ξ的所有可能取值为0，1，2，3，4，则4411()()(1)(0,1,2,3,4)33i ii P i C i ξ-==-=， ……………………………………9分所以16(0)81P ξ==，32(1)81P ξ==，24(2)81P ξ==，8(3)81P ξ==，1(4)81P ξ==， 则ξ的概率分布列如下：数学期望E ξ＝4×3＝3. ……………………………………14分 （或16322416140123481818181813E ξ=⨯+⨯+⨯+⨯+⨯=）. 21. 解：（I ）1123=12341234⨯⨯⨯⨯⨯⨯⨯⨯（－０），123=234512344⨯⨯⨯⨯⨯⨯⨯⨯４（－），[]1(1)(2)=(1)(2)(n 3)1)(1)(2)4n n n n n n n n n n +++++-++－(. …………………3分 （Ⅱ）由（I ）得1123=12341234⨯⨯⨯⨯⨯⨯⨯⨯（－０）， 123=234512344⨯⨯⨯⨯⨯⨯⨯⨯４（－）， ……[]1(1)(2)=(1)(2)(n 3)1)(1)(2)4n n n n n n n n n n +++++-++－(，H 相加得：1123234(1)(2)=(1)(2)(n 3)4n n n n n n ⨯⨯+⨯⨯+++++++，……………5分注意到32(1)(2)32n n n n n n ++=++，所以333322221233(123)2(123)n n n ++++++++++++++1(1)(2)(n 3)4n n n =+++， …………………6分 则由已知可求得：23333221123(1)4n S n n n =++++=+， …………………7分故1(1)2n S n n =+. …………………8分(Ⅲ)由1(1)2n S n n =+，得n a n =，221112(1)(1)()1n n n m b m m a a n n -=---=++-， 则2211212111111()()()()(2)()11111n n m m b b m n n n n n n n n n n +---=+--=-++--+++++ 1111111()(2)(2)11(1)1m m n n n n n n n n=-++-=---++++， ……………10分 因为1n n b b +>对任意n *∈N 恒成立，而1(1)n n + ＞0，所以11201m n n --->+对任意n *∈N 恒成立，即1121m n n<--+对任意n *∈N 恒成立， 设11()2(1)1g x x x x=--≥+ ，容易证明()g x 在[1,)+∞上单调递增，则当n ＝1时，min 11(2)1n n --+＝12，所以m ＜12.即实数m 的取值范围是1(,)2-∞． ………………………………………………………14分欢迎下载，资料仅供参考!!!。

2012～2013学年某某市高二期末调研测试数学（理科）数学Ⅰ试题一、填空题（本大题共14小题，每小题5分，共70分．请把答案填写在答题卡相应位置上．．．．．．．．） 1． 命题“,x ∀∈R sin 1x ≤”的否定是“▲”．2． 抛物线y 2= 4x 的准线方程为▲．解：∵2p=4，∴p=2，开口向右，∴准线方程是x=-1．故答案为x=-1． 3． 设复数22i(1i)z +=+（i 为虚数单位），则z 的虚部是▲．4． “1x <”是 “2log 0x <”的▲条件．(在“充分必要”、“充分不必要”、“必要不充分”、“既不充分也不必要”中选一个合适的填空)解：由log 2x ＜0，解得0＜x ＜1，所以“x＜1”是“log 2x ＜0”的必要不充分条件．故答案为：必要不充分． 5． 61()2x x-的二项展开式中的常数项是▲（用数字作答）．6． 若定义在R 上的函数()f x 的导函数为()24f x x '=-，则函数(1)f x -的单调递减区间是▲．7．口袋中有形状、大小都相同的2只白球和1只黑球，先摸出1只球，记下颜色后放回口袋，然后再摸出1只球，则“两次摸出的球颜色不相同”的概率是▲．8．已知正四棱柱ABCD-A1B1C1D1的对角线AC1的长为6，且AC1与底面所成角的余弦值为3，则该正四棱柱的体积为▲．39．某医院有内科医生5名，外科医生6名，现要派4名医生参加赈灾医疗队，如果要求内科医生和外科医生中都有人参加，则有▲种选法（用数字作答）．10．设m，n是两条不同的直线，α，β是两个不同的平面，给出下列命题：①若α∥β，m⊂β，n⊂α，则m∥n；②若α∥β，m⊥β，n∥α，则m⊥n；③若α⊥β，m⊥α，n⊥β，则m⊥n；④若α⊥β，m⊥α，n∥β，则m∥n．上面命题中，所有真命题．．．的序号为▲ ．11． 过椭圆22221(0)x y a b a b+=>>的焦点作垂直于x 轴的直线交椭圆于A ，B 两点，若AB =2a，则双曲线22221x y a b-=的离心率为▲．12． 已知圆221:()(1)1C x a y a -+--=和圆2222:(1)2C x y a -+=有两个不同的公共点，则实数a 的取值X 围是▲．13． 定义函数(),(),(),()K f x f x K f x K f x K >⎧=⎨⎩≤（K 为给定常数），已知函数225()3ln 2f x x x x =-，若对于任意的(0,)x ∈+∞，恒有()K f x K =，则实数K 的取值X 围为▲．14． 在下图中，从第2行起，除首末两个位置外，每个位置上的数都等于它肩上的两个数的和，最初几行是：则第▲行中有三个连续位置上的数之比是3︰4︰5．二、解答题（本大题共6小题，共90分，解答时应写出文字说明、证明过程或演算步骤．） 15．（本小题满分14分）如图，已知AB ⊥平面ACD ，DE ∥AB ，△ACD 是正三角形，AD = DE = 2AB = 2，且F 是CD 的中点．（1）求证：AF ∥平面BCE ；第1行 1 1 第2行 1 2 1 第3行 1 3 3 1 第4行 1 4 6 4 1 第5行 1 5 10 10 5 1 … …EBA（2）求证：平面BCE ⊥平面CDE ； （3）求四面体BCEF 的体积．16．（本小题满分14分）已知点M 到双曲线221169x y -=的左、右焦点的距离之比为2︰3．（1）求点M 的轨迹方程；（2）若点M 的轨迹上有且仅有三个点到直线y = x + m 的距离为4，某某数m 的值．17．（本小题满分14分）如图，在长方体ABCD -A 1B 1C 1D 1中，AB = 4，AD = 2，A 1A = 2，点F 是棱BC 的中点，点E 在棱C 1D 1上，且D 1E = λ EC 1（λ为实数）． （1）求二面角D 1-AC -D 的余弦值；（2）当λ =13时，求直线EF 与平面D 1AC 所成角的正弦值的大小；（3）求证：直线EF 与直线EA 不可能垂直．18．（本小题满分16分）有两枚均匀的硬币和一枚不均匀的硬币，其中不均匀的硬币抛掷后出现正面的概率为23．小华先抛掷这三枚硬币，然后小红再抛掷这三枚硬币． （1）求小华抛得一个正面两个反面且小红抛得两个正面一个反面的概率； （2）若用ξ表示小华抛得正面的个数，求ξ的分布列和数学期望； （3）求小华和小红抛得正面个数相同（包括0个）的概率． 19．（本小题满分16分）已知函数3211()(1)323a f x x a x x =-++-． （1）若函数()f x 的图象在点(2,(2))f 处的切线方程为90x y b -+=，某某数a ，b 的1111FED C B A D C B A （第17题）值；（2）若0a≤，求()f x的单调减区间；（3）对一切实数a∈(0,1)，求f(x)的极小值的最大值．20．（本小题满分16分）如图，点A（-a，0），B（23，43）是椭圆22221(0)x ya ba b+=>>上的两点，直线AB与y轴交于点C（0，1）．（1）求椭圆的方程；（2）过点C任意作一条直线PQ与椭圆相交于P，Q，求PQ的取值X围．2012～2013学年某某市高二期末调研测试数学Ⅰ（理科）参考答案2013．6一、填空题1．x∃∈R，sin1x> 2．x = -1 3．-1 4．必要不充分 5．5 2 -6．（-∞，3） 7．498．2 9．310 10．②③（第20题）1112．a <或a 13．233[e ,)2+∞ 14．62二、解答题 15．证明：（1）取EC 中点G ，连BG ，GF ．∵F 是CD 的中点，∴FG ∥DE ，且FG =12DE ． 又∵AB ∥DE ，且AB =12DE ．∴四边形ABGF 为平行四边形．……… 3分∴AF ∥BG ．又BG ⊂平面BCE ，AF ⊄平面BCE ． （条件每少一个扣1分，最多扣2分）∴AF ∥平面BCE ． …………5分（2）∵AB ⊥ 平面ACD ，AF ⊂平面ACD ，∴AB ⊥AF ．∵AB ∥DE ，∴AF ⊥DE ．………… 6分又∵△ACD 为正三角形，∴AF ⊥CD ．………… 7分 ∵BG ∥AF ，∴BG ⊥DE ，BG ⊥CD ．………… 8分 ∵CD ∩DE = D ，∴BG ⊥平面CDE ． ………… 9分（直接用AF ∥BG ，AF ⊥平面CDE ，而得到BG ⊥平面CDE ．扣1分） ∵BG ⊂平面BCE ，∴平面BCE ⊥平面CDE ；……………11分（3）四面体BCEF 的体积13CFE V S BG ∆=⋅1111123232CF DE AF =⨯⋅⋅=⨯⨯⨯ ……………14分 16．解：（1）双曲线221169x y -=的左、右焦点为1(5,0)F -，2(5,0)F ．………1分设点(,)M x y ，则1223MF MF =，23=． ……………3分化简得点M 的轨迹方程为2226250x y x +++=． ……………7分 （2）点M 的轨迹方程即为22(13)144x y ++=，它表示以(13,0)-为圆心，12为半径的圆． ……………9分 因为圆上有且仅有三点到直线y = x + m 的距离为4， 所以圆心到直线y = x + m 的距离为88=． ……………12分解得13m =± ……………14分 17．解：（1）如图所示，建立空间直角坐标系D xyz -．则(2,0,0),(0,4,0),A C 1(0,0,2),DG F EDCB A1(2,0,2)D A =-，1(0,4,2)D C =-． ………… 2分设平面1D AC 的法向量为(,,)x y z =n ， 则110,0D A D C ⋅=⋅=n n ．即,2x z z y ==．令1y =，则2x z ==．∴平面1D AC 的一个法向量(2,1,2)=n ．…… 4分 又平面DAC 的一个法向量为(0,0,1)=m ．故22cos ,||133⋅〈〉===⋅⨯m n m n m |n |，即二面角1D AC D --的余弦值为23． ……… 6分（2）当λ =13时，E （0，1，2），F （1，4，0），(1,3,2)EF =-．所以cos ,42||||143EF EF EF ⋅〈〉===⋅⨯n n n ． ……………9分因为 cos ,0EF 〈〉>n ，所以,EF 〈〉n 为锐角，从而直线EF 与平面1D AC ．……………10分 （3）假设EF EA ⊥，则0EF EA ⋅=．∵4(0,,2),(1,4,0)1E F λλ+，∴4(2,,2)1EA λλ=--+，4(1,4,2)1EF λλ=--+． ……………12分∴442(4)4011λλλλ--+=++．化简得23230λλ-+=．该方程无解，所以假设不成立，即直线EF 不可能与直线EA 不可能垂直．……14分18．解：（1）设A 表示事件“小华抛得一个正面两个反面”，B 表示事件“小红抛得两个正面一个反面”，则P （A ）=1111121()22232233⨯⨯⨯+⨯⨯=， …………2分P （B ）=1121115()222322312⨯⨯⨯+⨯⨯=， …………4分则小华抛得一个正面两个反面且小红抛得两个正面一个反面的概率为P （AB ）= P （A ）P （B ）=15531236⨯=． …………6分（2）由题意ξ的取值为0，1，2，3，且1111(0)22312P ξ==⨯⨯=；1(1)3P ξ==；5(2)12P ξ==；1121(3)2236P ξ==⨯⨯=．所求随机变量ξ的分布列为…………10分数学期望11515()01231231263E ξ=⨯+⨯+⨯+⨯=． …………12分 （3）设C 表示事件“小华和小红抛得正面个数相同”， 则所求概率为2222()(0)(1)(2)(3)P C P P P P ξξξξ==+=+=+=2222115123()()()()12312672=+++=． 所以“小华和小红抛得正面个数相同”的概率为2372． ………… 16分 19．解：（1）2()(1)1()f x ax a x a '=-++∈R ， …………1分由(2)9f '=，得a = 5．…………2分∴3251()333f x x x x =-+-．则(2)3f =．则（2，3）在直线90x y b -+=上．∴b = -15． …………4分（2）① 若0a =，221111()(1)2326f x x x x =-+-=--+，∴()f x 的单调减区间为（1，+∞）．…………6分 ② 若0a <，则21()(1)1()(1),,f x ax a x a x x x a'=-++=--∈R令()0f x '<，得1()(1)0x x a -->．∴1x a<，或x ˃ 1． …………9分∴()f x 的单调减区间为1(,)a -∞，（1，+∞）． …………10分（3）1()(1)()f x a x x a'=--，0 ˂a ˂ 1，∴f (x ) 的极小值为32111111()(1)323a f a a a a a=⋅-++-22111111131()6236224a a a =-⋅+⋅-=--+．…………14分 当23a =时，函数f (x ) 的极小值f (1a )取得最大值为124．…………16分 20．解：（1）由B （23，43），C （0，1），得直线BC 方程为112y x =+．………… 2分令y = 0，得x = -2，∴a = 2． ………… 3分将B （23，43）代入椭圆方程，得24169914b +=．∴b 2= 2．椭圆方程为22142x y +=． ………… 5分（2）① 当PQ 与x 轴垂直时，PQ= ………… 6分② 当PQ 与x 轴不垂直时，不妨设直线PQ ：y = kx + 1（k ≥0）， 代入椭圆方程x 2+ 2y 2- 4 = 0，得x 2+ 2(kx + 1)2- 4 = 0．即 (2k 2+ 1) x 2+ 4kx - 2 = 0． ………… 8分 设P (x 1，y 1)，Q (x 2，y 2)，则1,221x k =+． 则 | x 1 -x 2．PQ．………… 10分 2242222242428(1)(41)45188(1)(21)441441k k k k k PQ k k k k k ++++==⋅=⋅++++++=2218(1)144k k⋅+++．………… 12分∵22144k k +≥，在k时取等号， ………… 14分 ∴PQ 2= 2218(1)144k k⋅+++∈（8，9]．则PQ∈． ………… 15分由①，②得PQ 的取值X围是． ………… 16分数学Ⅱ（理科附加题）参考答案A 1 证明：如图，连结BP ，∵AB = AC ，AD 是BC 边的中线，∴AD 是此等腰三角形的一条对称轴． ∴ABP ACP ∠=∠． ………… 2分 ∵BF ∥AC ，∠F = ∠ACP ．∴∠F = ∠ABP ． ………… 5分 又BPF EPB ∠=∠，∴BPF ∆∽EPB ∆． ………… 8分所以BP PF PE BP=，即2BP PE PF =⋅． ∵BP = CP ，∴CP 2= PE ·PF ． ……… 10分A 2 证明：（1）连结ED ．∵AF 为切线，∴∠FAB = ∠ACB ．………… 2分∵BD AC ⊥，CE AB ⊥，∴90AEF BDC ∠=∠=．∴F DBC ∠=∠． ………… 5分（2）∵BD AC ⊥，CE AB ⊥，∴,,,D E B C 四点共圆．则DEC DBC ∠=∠．又F DBC ∠=∠，∴DEC F ∠=∠．则DE ∥AF ． ……………8分 ∴AD FE DC EC =，即AD EC DC FE ⋅=⋅． ……… 10分B 1 解：由题设得010110101001MN -⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦． ………… 2分 设直线210x y -+=上任意一点(,)x y 在矩阵MN 对应的变换作用下变为(,)x y ''，则 1001x x y y '⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥'-⎣⎦⎣⎦⎣⎦． ………… 5分 即x x y y '⎡⎤⎡⎤=⎢⎥⎢⎥'-⎣⎦⎣⎦，∴,.x x y y '=⎧⎨'=-⎩………… 8分 ∵点(,)x y 在直线210x y -+=上，∴2()10x y ''--+=，即210x y ''++=． ∴曲线F 的方程为210x y ++=． ………… 10分B 2 解：（1）由题意得1112011a b ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦．………… 2分 即122a b +⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦，∴12,2.a b +=⎧⎨=⎩ 则1,2a b ==．………… 5分（2）由（1）得矩阵M 1102⎡⎤=⎢⎥⎣⎦， 矩阵M 的特征多项式为()()11()1202f λλλλλ--==---， 矩阵M 的另一个特征值是1．代入二元一次方程组()()10020x y x y λλ--=⎧⎪⎨⋅+-=⎪⎩，解得0y =， 于是M 的属于特征值1的一个特征向量为10⎡⎤⎢⎥⎣⎦． ………… 8分 ∴α=11210⎡⎤⎡⎤+⎢⎥⎢⎥⎣⎦⎣⎦． ∴M 10α= M 10101011111026222110101024⎛⎫⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+=+⋅= ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎝⎭．………… 10分C 1解：圆C 的直角坐标方程为2220x y x +-=，即22(1)1x y -+=． ………… 2分 圆心(1,0)C ，直线l 的直角坐标方程为40x y --=． ………… 5分 所以过点C 与直线l 垂直的直线的方程为10x y +-=． ………… 8分化为极坐标方程得cos sin 10ρθρθ+-=，即cos()4πρθ-=．………… 10分C 2 解：（1）直线l 的普通方程0x y m --=，椭圆C 的普通方程为2213x y +=； …………………… 2分 （2）设椭圆C 上一点P的坐标为[)(),sin )0,2αααπ∈，∵m ˃ 2，∴点P 到直线l 的距离d =2cos 2m πα⎛⎫-+ ⎪==．∴2cos 6m πα⎛⎫=++ ⎪⎝⎭ …………………… 5分 ∵椭圆C 上有且只有1个点到直线l 的距离为2，∴关于α的方程2cos 6m πα⎛⎫=++ ⎪⎝⎭[)0,2π上有且只有一个解．∴2m =+2m =-+． …………………… 8分若2m =+2m >，此时116πα=，点P 的坐标是31,22⎛⎫- ⎪⎝⎭；若22m =-+，不合题意．综上，实数m的值为2+31,22⎛⎫- ⎪⎝⎭．……………10分D 1证明：（1）当2n =时，因为0x ≠，()2211212x x x x +=++>+，即n = 2时不等式成立； ……… 2分（2）假设n = k （2,*k k ∈N ≥）时不等式成立，即有()11k x kx +>+，则当1n k =+时，()()()()()111111k kx x x x kx ++=++>++……… 5分 ()2111x kx kx k x =+++>++． ……… 8分即当1n k =+时，不等式也成立．综合（1）（2）可知，原不等式成立． ……… 10分D 2（1）证明：由柯西不等式得()()222222222222149123a b c a b c a b c a b c ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫++⋅++=++⋅++⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦………… 2分 212336a b c a b c ⎛⎫⋅+⋅+⋅= ⎪⎝⎭≥． ∵2221a b c ++=，∴22214936a b c++≥． …………………… 5分 （2）解：由（1）得236m m +-≤．当m ≥2时，m +m - 2≤36，∴m ≤19；当02m <<时，m + 2 -m ≤36，恒成立；当m ≤0时，-m + 2 -m ≤36，∴m ≥-17． …………………… 8分 综上，实数m 的取值X 围是[-17，19]． …………………… 10分。

2012-2013年度第二学期高二期末检测数学（理）第Ⅰ卷一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1、复数z 满足()2z i i i -=+，则z =（ ）A ．1i --B ．1i -C ．13i -+D ．1i --2、函数()()()f x x a x b =--在x a =处的导数为（ ）A ．abB ．()a a b --C ．0D ．a b -3、已知速记变量ζ服从正态分布2(1,)N σ，若(4)0.79P ζ≤=，则(2)P ζ≤-=（ ）A ．0.29B ．0.21C ．0.19D ．0.794、设某种动物的体重y （单位：千克）与身长x （单位：厘米）具有线性相关关系，根据一组样本数据建立的回归直线方程为ˆ0.8585.71y=-，则下列结论中不正确的是（ ） A ．y 与x 具有正的线性相关关系B ．回归直线必定经过样本中心点（,x y ）C ．若某一只该中动物身长增加1厘米，则其体重约增加0.85千克；D ．若某一只该种动物身长170厘米，则体重必定为58.79千克。

5、给出下列定积分：①20sin xdx π⎰ ②02sin xdx π⎰ ③23xdx -⎰ ④231x dx -⎰，其中为负值的个数为（ ） A ．1 B ．2 C ．3 D ．46、若8280128(1)(1)(1)(1)x a a x a x a x -=+++++++，则6a =（ ）A ．112B ．28C ．-28D ．-1127、一条长椅上有9个座位，三个人来坐，若相邻两个人之间至少有两个空座位，则不同的坐法种数为（ ）A ．60B ．24C ．36D ．1208、通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：参考附表，得到的正确结论是：A ．有99%以上的把握认为“爱好该项运动与性别有关”B ．有99%以上的把握认为“爱爱好该项运动与性别无关”C ．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”D ．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”9、已知函数()y xf x '=的图象如图（1）所示（其中()f x '是函数()f x 的导函数），下面四个图象中，()y f x =的图象大致是（ ）10、设,m n 分别是先后抛掷一枚骰子所得到的点数，则先后两次出现的点数中有5的情况下，方程20x mx n ++=有实根的概率是（ ）A ．1136B ．736C ．711D ．710 11、函数()sin cos ()f x x x x R =+∈的图象向左平移()m m R +∈个单位后，得到函数()y f x '=的图象，则m 的最小值为（ ）A ．4πB ．2πC ．πD ．6π 12、函数()32(1)48(3)f x ax a x b x b =+-+-+的图象关于原点中心对称，则()f x （ ）A ．在[-上为增函数B ．在[-上为减函数C ．在)+∞上为增函数，在(-∞为减函数D ．在(-∞上为增函数，在)+∞为减函数第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分，把答案填在答题卷的横线上。