新人教版八年级第十三章《轴对称》知识点及典型例题(精.选)

第十三章轴对称一、知识框架：二、知识清单：1.轴对称：⑴轴对称图形：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形.这条直线称为它的对称轴.⑵两个图形成轴对称：把一个图形沿某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称.这条直线称为这两个图形的对称轴.⑶线段的垂直平分线：经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线.2.轴对称的性质：对称的性质：①两个图形关于某一条直线对称，对称轴是任何一对对应点所连线段的垂直平分线.轴对称图形的对称轴是任何一对对应点连线段的垂直平分线.②关于某直线对称的两个图形是全等形.3.线段垂直平分线性质①线段垂直平分线上的点与这条线段两个端点的距离相等.②与一条线段两个端点距离相等的点在这条线段的垂直平分线上.③线段垂直平分线的作图a 分别以线段的两个端点为圆心，大于1/2线段的适当长度为半径画弧，两弧交于两个点；b 过两个交点作直线，则直线即为已知线段的垂直平分线.4.画已知图形的轴对称图形（步骤）a 过已知点A 作对称轴l 的垂线，垂足为O ，在垂线上截取OA'，使OA'=OA ，则点A'是点A 的对称点；b 同理分别作出其它关键点的对称点；c 将所作的对称点依次相连，得到轴对称图形.5.关于坐标轴对称的点的坐标性质①关于x 轴对称的点横坐标不变，纵坐标互为相反数； 点P (,)x y 关于x 轴对称的点的坐标为'P (,)x y -.②关于y 轴对称的点纵坐标不变，横坐标互为相反数； 点P (,)x y 关于y 轴对称的点的坐标为"P (,)x y -.③关于原点对称的点横纵坐标分别互为相反数；点P (,)x y 关于原点对称的点的坐标为P 1()y ,x --.6.等腰三角形（1）等腰三角形：有两条边相等的三角形叫做等腰三角形.相等的两条边叫做腰，另一条边叫做底边，两腰所夹的角叫做顶角，底边与腰的夹角叫做底角.（2）等腰三角形的性质（定理）：①等腰三角形的两个底角相等（简写成“等边对等角”）.②等腰三角形的顶角角平分线、底边上的中线，底边上的高相互重合.（简写成“三线合一”）（3）等腰三角形的判定（定理）如果一个三角形有两个角相等，那么这两个角所对的边也相等。

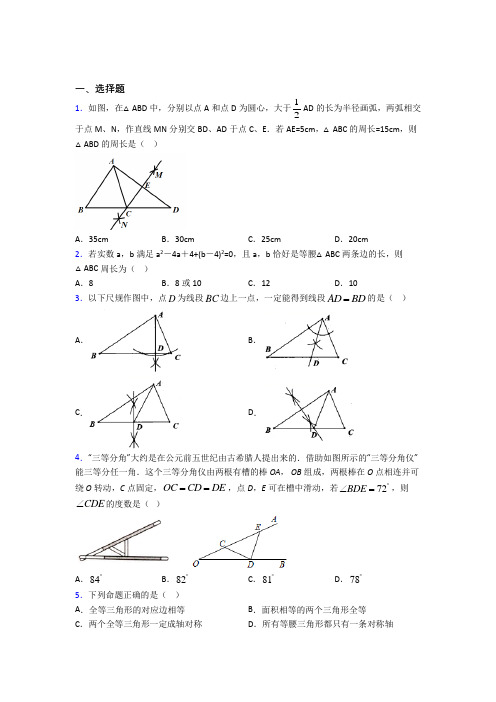
一、选择题1．如图，在△ABD 中，分别以点A 和点D 为圆心，大于12AD 的长为半径画弧，两弧相交于点M 、N ，作直线MN 分别交BD 、AD 于点C 、E ．若AE=5cm ，△ABC 的周长=15cm ，则△ABD 的周长是（ ）A ．35cmB ．30cmC ．25cmD ．20cm2．若实数a ，b 满足a 2－4a ＋4+(b －4)2=0，且a ，b 恰好是等腰△ABC 两条边的长，则△ABC 周长为（ ） A ．8B ．8或10C ．12D ．103．以下尺规作图中，点D 为线段BC 边上一点，一定能得到线段AD BD =的是（ ）A ．B ．C ．D ．4．“三等分角”大约是在公元前五世纪由古希腊人提出来的．借助如图所示的“三等分角仪”能三等分任一角．这个三等分角仪由两根有槽的棒OA ， OB 组成，两根棒在O 点相连并可绕O 转动，C 点固定，OC CD DE ==，点D ，E 可在槽中滑动，若72BDE ︒∠=，则CDE ∠的度数是（ ）A ．84︒B ．82︒C ．81︒D ．78︒5．下列命题正确的是（ ） A ．全等三角形的对应边相等 B ．面积相等的两个三角形全等 C ．两个全等三角形一定成轴对称D ．所有等腰三角形都只有一条对称轴6．下列命题中，是假命题的是（ ） A ．能够完全重合的两个图形全等 B ．两边和一角对应相等的两个三角形全等 C ．三个角都相等的三角形是等边三角形D ．等腰三角形的两底角相等7．已知点A 是直线l 外的一个点，点B ，C ，D ，E 是直线l 上不重合的四个点，再添加①AB AC =；②AD AE =；③BD CE =中的两个作为题设，余下的一个作为结论组成一个命题，组成真命题的个数为（ ）． A ．0B ．1C ．2D ．38．如图，在ABC ∆中，90,30C B ︒︒∠=∠= ，以A 为圆心，任意长为半径画弧分别交AB AC 、于点M 和N ，再分别以M N 、为圆心，大于12MN 的长为半径画弧，两弧交于点P ，连接AP ，并延长交BC 于点D ，则下列说法中正确的个数是（ ）①AD 是BAC ∠的平分线；②60ADC ︒∠=；③点D 在AB 的垂直平分线上﹔④若2AD =，则点D 到AB 的距离是1，:1:2DAC ABC S S ∆∆=A ．2B ．3C ．4D ．59．如图，在ABC 中，AB AC =，D 为BC 的中点，AD AE =，若40BAD ∠=︒，则CDE ∠的度数为（ ）A ．10︒B ．20︒C ．30D ．40︒10．如图，ABC 是等边三角形，D 是线段BC 上一点（不与点,B C 重合），连接AD ，点,E F 分别在线段,AB AC 的延长线上，且DE DF AD ==，点D 从B 运动到C的过程中，BED 周长的变化规律是（ ）A ．不变B ．一直变小C ．先变大后变小D ．先变小后变大11．如图，长方形纸片ABCD （长方形的对边平行且相等，每个角都为直角），将纸片沿EF 折叠，使点C 与点A 重合，下列结论：①AF AE =，②ABE AGF ≌，③AF CE =，④60AEF ∠=︒，其中正确的（ ）A ．①②B ．②③C ．①②③D ．①②③④ 12．平面直角坐标系中，点A (3，2)与点B 关于y 轴对称，则点B 的坐标为（ ） A ．(3，－2)B ．(－3，－2)C ．(－3，2)D ．(－2，3)13．如图，已知等腰三角形ABC 中，AB AC =，15DBC ∠=︒，分别以A 、B 两点为圆心，以大于12AB 的长为半径画圆弧，两弧分别交于点E 、F ，直线EF 与AC 相交于点D ，则A ∠的度数是（ ）A ．50°B ．60°C ．75°D ．45°14．如图，在ABC 中，18cm AC =，20cm BC =，点M 从点A 出发以每秒2cm 的速度向点C 运动，点N 从点C 出发以每秒1.6cm 的速度向点B 运动，其中一个动点到达终点时，另一个动点也随之停止运动，当CMN △是以MN 为底的等腰三角形时，则这时等腰三角形的腰长是（ ）A ．5cmB ．6cmC ．7cmD ．8cm15．下列图案中，是轴对称图形的是（ ）A ．B ．C ．D ．二、填空题16．如图，点CD 在线段AB 的同侧，CA =6，AB =14，BD =12，M 为AB 中点，∠CMD =120°．则CD 的最大值为____．17．平面直角坐标系xOy 中，先作出点P (2,3)-关于y 轴的对称点，再将该对称点先向下平移1个单位，再向左平移2个单位得到点P 1，称为完成一次图形变换，再将点P 1进行同样的图形变换得到点P 2，以此类推，则点P 2020的坐标为___________．18．如图，等腰ABC 的周长为36，底边上的高12AD =，则ABD △的周长为________．19．如图，在ABC ∆中，CD 平分,ACB ∠点,E F 分别是,CD AC 上的动点．若6,12,ABC BC S ∆==则AE EF +的最小值是______________．20．如图，已知30MON ∠=︒，点1A ，2A ，3A ，…在射线ON 上，1B ，2B ，3B ，…在射线OM 上，112A B A △，223A B A △，334A B A △，…均为等边三角形；若48OA =，则1n n n A B A +△的边长为______．21．在平面直角坐标系中，O 为坐标原点，()1,1A ，在x 轴上确定一点P ，使AOP 为等腰三角形，则符合条件的等腰三角形的顶角度数为______． 22．在△ABC 中，按以下步骤作图：①分别以A ，C 为圆心，以大于12AC 的同样长为半径画弧，两弧相交于两点M ，N ； ②作直线MN 交AB 于点D ，连结CD ．请回答：若BC=DC ，∠B=100°，则∠ACB 的度数为____．23．如图，在等边△ABC 中，AC ＝9，点O 在AC 上，且AO ＝3，点P 是AB 上一动点，连接OP ，以O 为圆心，OP 长为半径画弧交BC 于点D ，连接PD ，如果PO ＝PD ，那么AP 的长是________．24．如图，已知∠AOB=60°，点P 在边OA 上，OP=24，点M ，N 在边OB 上，PM=PN ，若NM=6，则OM=______________．25．如图，在Rt ABC 中，90ACB ∠=︒，30A ∠=︒，BD 平分ABC ∠，如果9cm AC =，那么AD = ___________cm ．26．如图，网格纸上每个小正方形的边长为1，点A ，点C 均在格点上，点P 为x 轴上任意一点，则PAC △周长的最小值为________．三、解答题27．如图，在△ABC 中， AB =AC ．过点A 作BC 的平行线交∠ABC 的角平分线于点D ，连接CD ．(1)求证：△ACD 为等腰三角形． (2)若∠BAD =140°，求∠BDC 的度数．28．已知ABC 是等边三角形，点D 是AC 的中点，点P 在射线BC 上，点Q 在线段AB 上，120PDQ ∠=︒．（1）如图1，若点Q 与点B 重合，求证：DB DP =；（2）如图2，若点P 在线段BC 上，8AC =，求AQ PC +的值．29．在如图所示的直角坐标系中，每个小方格都是边长为1的正方形，ABC 的顶点均在格点上，点A 的坐标是(3,1)--．（1）将ABC 关于x 轴对称得到111A B C △，画出111A B C △，并写出点1B 的坐标； （2）把111A B C △平移，使点B 平移到2(3,4)B ，请作出111A B C △平移后的222A B C △，并写出2A 的坐标；（3）已知ABC 中有一点(,)D a b ，求222A B C △中的对应点2D 的坐标．30．如图，在ABC 中，45B ︒∠=，60C ︒∠=，点E 为线段AB 的中点，点F 在边AC 上，连结EF ，沿EF 将AEF 折叠得到PEF ．（1）如图1，当点P 落在BC 上时，求AEP ∠的度数． （2）如图2，当PF AC ⊥时，求BEP ∠的度数．。

第十三章（精编）轴对称《轴对称、线段垂直平分线、、等腰三角形、等边三角形》轴对称图形如果一个图形沿某一条直线折叠，直线两旁的部分能够互相重合，•这个图形就叫做轴对称图形，这条直线就是它的对称轴．有的轴对称图形的对称轴不止一条，如圆就有无数条对称轴．轴对称有一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，•那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点，叫做对称点．两个图形关于直线对称也叫做轴对称．图形轴对称的性质如果两个图形成轴对称，•那么对称轴是任何一对对应点所连线段的垂直平分线；轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线．画一图形关于某条直线的轴对称图形的步骤：找到关键点，画出关键点的对应点，按照原图顺序依次连接各点。

轴对称与轴对称图形的区别轴对称是指两个图形之间的形状与位置关系，•成轴对称的两个图形是全等形；轴对称图形是一个具有特殊形状的图形，把一个轴对称图形沿对称轴分成两个图形，这两个图形是全等形，并且成轴对称．考点一、关于“轴对称图形”与“轴对称”的认识1.下列几何图形中，○1线段○2角○3直角三角形○4半圆，其中一定是轴对称图形的有【】A．1个B．2个C．3个D．4个2．图中，轴对称图形的个数是【】A．4个 B．3个 C．2个 D．1个3．正n 边形有___________条对称轴，圆有_____________条对称轴线段的垂直平分线 （1）经过线段的中点并且垂直于这条线段的直线，•叫做这条线段的垂直平分线（或线段的中垂线）．（2）线段的垂直平分线上的点与这条线段两个端点的距离相等；反过来，•与一条线段两个端点距离相等的点在这条线段的垂直平分线上．因此线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合．考点二、线段垂直平分线的性质4．如图，△ABC 中，∠A ＝90°，BD 为∠ABC 平分线，DE ⊥BC ，E 是BC 的中点，求∠C 的度数。

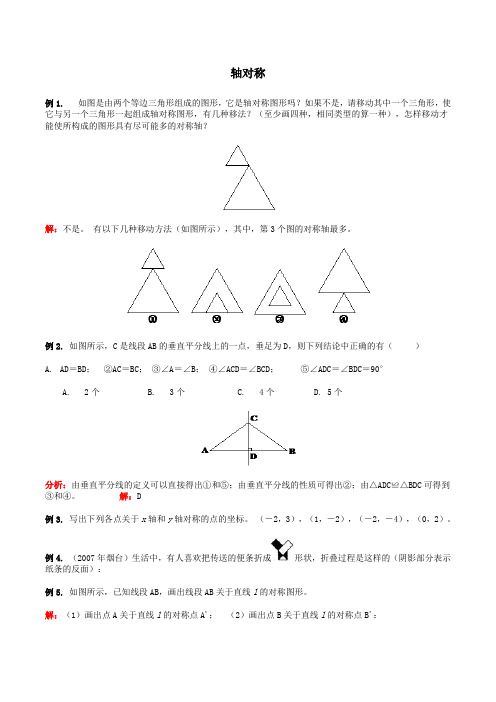
轴对称例1.如图是由两个等边三角形组成的图形，它是轴对称图形吗？如果不是，请移动其中一个三角形，使它与另一个三角形一起组成轴对称图形，有几种移法？（至少画四种，相同类型的算一种），怎样移动才能使所构成的图形具有尽可能多的对称轴？解：不是。

有以下几种移动方法（如图所示），其中，第3个图的对称轴最多。

例2. 如图所示，C是线段AB的垂直平分线上的一点，垂足为D，则下列结论中正确的有（）A.AD＝BD；②AC＝BC；③∠A＝∠B；④∠ACD＝∠BCD；⑤∠ADC＝∠BDC＝90°A. 2个B. 3个C. 4个D. 5个分析：由垂直平分线的定义可以直接得出①和⑤；由垂直平分线的性质可得出②；由△ADC≌△BDC可得到③和④。

解：D例3. 写出下列各点关于x轴和y轴对称的点的坐标。

（－2，3），（1，－2），（－2，－4），（0，2）。

例4.（2007年烟台）生活中，有人喜欢把传送的便条折成形状，折叠过程是这样的（阴影部分表示纸条的反面）：例5. 如图所示，已知线段AB，画出线段AB关于直线l的对称图形。

解：（1）画出点A关于直线l的对称点A'；（2）画出点B关于直线l的对称点B'：（3）连结A'B'，则线段A'B'即为所求。

例6.要在河边修建一个水泵站，分别向张村、李庄送水（如图）。

修在河边什么地方，可使所用水管最短？解：设张村为点A，李庄为点B，张村和李庄这一侧的河岸为直线l。

（1）作点B关于直线l的对称点，（2）连结，交直线l于点C，点C就是所求的水泵站的位置。

（如图所示）1. 下列说法错误的是（）A. 关于某直线对称的两个图形一定能完全重合B. 全等的两个三角形一定关于某直线对称C. 轴对称图形的对称轴至少有一条D. 线段是轴对称图形2. 轴对称图形的对称轴是（）A. 直线B. 线段C. 射线D. 以上都有可能3. 下面各组点关于y轴对称的是（）A. （0，10）与（0，－10）B. （－3，－2）与（3，－2）C. （－3，－2）与（3，2）D. （－3，－2）与（－3，2）*4. 下列图形中，不是轴对称图形的是（）A. 一条线段B. 两条相交直线C. 有公共端点的两条相等的线段D. 有公共端点的两条不相等的线段5. （2007年河南）如图，ΔABC与ΔA'B'C'关于直线l对称，则∠B的度数为（）A. 30°B. 50°C. 90°D. 100°6. （2008年江苏苏州）下列图形中，是轴对称图形的是（）*7. （2008年武汉）如图，六边形ABCDEF是轴对称图形，CF所在的直线是它的对称轴，若∠AFC＋∠BCF ＝150°，则∠AFE＋∠BCD的大小是（）A. 150°B. 300°C. 210°D. 330°**8. （2008年全国数学竞赛浙江预赛）如图，直线l1与直线l2相交，∠α＝60°，点P在∠α内（不在l1，l2上）。

第十三章轴对称知识点常见考点例析一.知识框架图二.轴对称和轴对称图形1、有一个图形沿着某一条直线折叠，如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点，叫做对称点．两个图形关于直线对称也叫做轴对称．2、轴对称图形：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形。

这条直线就是它的对称轴。

（对称轴必须是直线）3、对称点：折叠后重合的点是对应点，叫做对称点。

4、轴对称图形的性质：如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

类似的，轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

连接任意一对对应点的线段被对称轴垂直平分．轴对称图形上对应线段相等、对应角相等。

5．画一图形关于某条直线的轴对称图形步骤：找到关键点，画出关键点的对应点，按照原图顺序依次连接各点。

三.轴对称与轴对称图形的区别和联系区别：轴对称是指两个图形之间的形状与位置关系，成轴对称的两个图形是全等形；轴对称图形是一个具有特殊形状的图形，把一个轴对称图形沿对称轴分成两个图形，这两个图形是全等形，并且成轴对称．联系：1：都是折叠重合 2;如果把成轴对称的两个图形看成一个图形那么他就是轴对称图形，反之亦然。

线段的垂直平分线经过线段的中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线（或线段的中垂线）（2）线段的垂直平分线上的点与这条线段两个端点的距离相等；反过来，与一条线段两个端点距离相等的点在这条线段的垂直平分线上．（证明是必须有两个点）因此线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合．四.用坐标表示轴对称1、点（x，y）关于x轴对称的点的坐标为（-x，y）2、点（x，y）关于y轴对称的点的坐标为（x，-y）；五.关于坐标轴夹角平分线对称点P（x，y）关于第一、三象限坐标轴夹角平分线y＝x对称的点的坐标是（y，x）点P（x，y）关于第二、四象限坐标轴夹角平分线y＝－x对称的点的坐标是（－y，－x）六.关于平行于坐标轴的直线对称点P（x，y）关于直线x＝m对称的点的坐标是（2m－x，y）；点P（x，y）关于直线y＝n对称的点的坐标是（x，2n－y）；。

第十三章《轴对称》一、知识点归纳（一）轴对称和轴对称图形1、有一个图形沿着某一条直线折叠，如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点，叫做对称点．两个图形关于直线对称也叫做轴对称．2、轴对称图形：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形。

这条直线就是它的对称轴。

（对称轴必须是直线）3、对称点：折叠后重合的点是对应点，叫做对称点。

4、轴对称图形的性质：如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

类似的，轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

连接任意一对对应点的线段被对称轴垂直平分．轴对称图形上对应线段相等、对应角相等。

5．画一图形关于某条直线的轴对称图形步骤：找到关键点，画出关键点的对应点，按照原图顺序依次连接各点。

（二）、轴对称与轴对称图形的区别和联系区别：轴对称是指两个图形之间的形状与位置关系，成轴对称的两个图形是全等形；轴对称图形是一个具有特殊形状的图形，把一个轴对称图形沿对称轴分成两个图形，这两个图形是全等形，并且成轴对称．联系：1：都是折叠重合2;如果把成轴对称的两个图形看成一个图形那么他就是轴对称图形，反之亦然。

（三）线段的垂直平分线（1）经过线段的中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线（或线段的中垂线）（2）线段的垂直平分线上的点与这条线段两个端点的距离相等；反过来，与一条线段两个端点距离相等的点在这条线段的垂直平分线上．（证明是必须有两个点）因此线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合．（四）用坐标表示轴对称1、点（x，y）关于x轴对称的点的坐标为（-x，y）；2、点（x，y）关于y轴对称的点的坐标为（x，-y）；(五）关于坐标轴夹角平分线对称点P（x，y）关于第一、三象限坐标轴夹角平分线y＝x对称的点的坐标是（y，x）点P（x，y）关于第二、四象限坐标轴夹角平分线y＝－x对称的点的坐标是（－y，－x）（六）关于平行于坐标轴的直线对称点P（x，y）关于直线x＝m对称的点的坐标是（2m－x，y）；点P（x，y）关于直线y＝n对称的点的坐标是（x，2n－y）；(七）等腰三角形1、等腰三角形性质：性质1：等腰三角形的两个底角相等（简写成“等边对等角”）性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合。

一、选择题1．已知一个等腰三角形两个内角度数之比为1：4，则这个等腰三角形顶角度数为（ ） A ．75°B ．90°C ．105°D ．120°或20°D 解析：D【分析】设两内角的度数为x 、4x ，分两种情况，列出方程，即可求解．【详解】解：设两内角的度数为x 、4x ，当等腰三角形的顶角为x 时，x ＋4x ＋4x ＝180°，x ＝20°；当等腰三角形的顶角为4x 时，4x ＋x ＋x ＝180°，x ＝30°，4x ＝120°；因此等腰三角形的顶角度数为20°或120°．故选：D ．【点睛】本题考查了等腰三角形的性质，掌握分类讨论思想方法是解题的关键．2．如图所示，已知ABC 和DCE 均是等边三角形，点B 、C 、E 在同一条直线上，连接AE 、BD 、FG ，AE 与BD 交于点O ，AE 与CD 交于点G ，AC 与BD 交于点F ，则下列结论中：①AE BD =； ②AG BF =； ③FG//BE ； ④CF CG =，以上结论正确的有（ ）A ．1个B ．2个C ．3个D ．4个D解析：D【分析】 首先根据等边三角形性质得出BC=AC ，CD=CE ，∠ACB=∠ECD=60°，即可证明△BCD 与△ACE 全等、△BCF 与△ACG 全等以及△DFC 与△EGC 全等，最后利用全等三角形性质以及等边三角形性质证明即可．【详解】∵△ABC 与△CDE 为等边三角形，∴BC=AC ，CD=CE ，∠ACB=∠ECD=60°，∴∠ACB+∠ACD=∠ACD+∠ECD ，∠ACD=60°，即：∠ACE=∠BCD ，在△BCD 与△ACE 中，∵BC=AC ，∠ACE=∠BCD ，CD=CE ，∴△BCD ≌△ACE(SAS)，∴AE=BD ，即①正确；在△BCF 与△ACG 中，由①可知∠CBF=∠CAG ，又∵AC=BC ，∠BCF=∠ACG=60°，∴△BCF ≌△ACG(ASA)，∴AG=BF ，即②正确；在△DFC 与△EGC 中，∵△BCF ≌△ACG ，∴CF=CG ．即④正确；∵∠GCF =60°，∴△CFG 为等边三角形，∴∠CFG=∠FCB=60°，∴FG ∥BE ，即③正确；综上，①②③④都正确．故选：D ．【点睛】本题考查了等边三角形的性质，全等三角形的判定和性质以及平行线的判定，解题的关键是正确寻找全等三角形来解决问题，．3．已知点A 的坐标为()1,3，点B 的坐标为()2,1，将线段AB 沿坐标轴翻折180°后，若点A 的对应点A '的坐标为()1,3-，则点B 的对应点B '的坐标为（ ）A ．()2,2B ．(2,1)-C ．()2,1-D ．(2,1)-- C解析：C【分析】根据点A ，点A'坐标可得点A ，点A'关于y 轴对称，即可求点B'坐标．【详解】解：∵将线段AB 沿坐标轴翻折后，点A （1，3）的对应点A′的坐标为（-1，3）， ∴线段AB 沿y 轴翻折，∴点B 关于y 轴对称点B'坐标为（-2，1）故选：C ．【点睛】本题考查了翻折变换，坐标与图形变化，熟练掌握关于y 轴对称的两点纵坐标相等，横坐标互为相反数是关键．4．等腰三角形的一个内角是50度，它的一腰上的高与底边的夹角是（ ）度A ．25或60B ．40或60C ．25或40D ．40C解析：C【分析】当顶角为50°时和底角为50°两种情况进行求解．【详解】当顶角为50°时，底角为：（180°−50°）÷2＝65°．此时它的一条腰上的高与底边的夹角为：90°−65°＝25°．当底角为50°时，此时它的一条腰上的高与底边的夹角为：90°−50°＝40°．故选：C ．【点睛】本题考查等腰三角形的性质，等腰三角形中两个底角相等．同时考查了分类讨论的思想． 5．如图所示，D 为 BC 上一点，且 AB ＝AC ＝BD ，则图中∠1 与∠2 的关系是（ ）A ．∠1＝2∠2B ．∠1+∠2＝180°C ．∠1+3∠2＝180°D ．3∠2﹣∠1＝180°D 解析：D【分析】根据三角形外角的性质得12C ∠+∠=∠，再根据等腰三角形的性质得B C ∠=∠，2BAD ∠=∠，由180BAC B C ∠+∠+∠=︒即可得出1∠与2∠的关系．【详解】解：∵2∠是ACD △的外角，∴12C ∠+∠=∠，∴∠C=∠2-∠1，∵AB AC =，∴B C ∠=∠，∵AB BD =，∴2BAD ∠=∠，∴112BAC BAD ∠=∠+∠=∠+∠，∵180BAC B C ∠+∠+∠=︒，∴122121180∠+∠+∠-∠+∠-∠=︒，即321180∠-∠=︒．故选：D ．【点睛】本题考查等腰三角形的性质，解题的关键是利用等腰三角形的性质得到相等的角． 6．如图，C 是线段AB 上的一点，ACD △和BCE 都是等边三角形，AE 交CD 于M ，BD 交CE 于N ，交AE 于O ，则①DB AE =；②AMC DNC ∠=∠；③60AOB ∠=︒；④DN AM =；⑤CMN △是等边三角形．其中，正确的有（ ）A ．2个B ．3个C ．4个D ．5个C解析：C【分析】 易证△ACE ≌△DCB ，可得①正确；即可求得∠AOB ＝120°，可得③错误；再证明△ACM ≌△DCN ，可得②④正确和CM ＝CN ，即可证明⑤正确；即可解题．【详解】解：∵ACD △和BCE 都是等边三角形∵∠ACD ＝∠BCE ＝60°，∴∠DCE ＝60°，在△ACE 和△DCB 中，AC DC ACE DCB CB CE =⎧⎪∠=∠⎨⎪=⎩，∴△ACE ≌△DCB （SAS ），∴∠BDC ＝∠EAC ，DB ＝AE ，①正确；∠CBD ＝∠AEC ，∵∠AOB ＝180°−∠OAB−∠DBC ，∴∠AOB ＝180°−∠AEC−∠OAB ＝120°，③错误；在△ACM 和△DCN 中，60BDC EAC DC ACACD DCN ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩， ∴△ACM ≌△DCN （ASA ），∴AM ＝DN ，④正确；∠AMC ＝∠DNC ，②正确；CM ＝CN ，∵∠ACD ＝∠BCE ＝60°，∴∠MCN ＝180°-∠ACD-∠BCE =60°，∴△CMN 是等边三角形，⑤正确；故有①②④⑤正确．故选：C ．【点睛】本题考查了全等三角形的判定和全等三角形对应边、对应角相等的性质，本题中求证△ACE ≌△DCB 和△ACM ≌△DCN 是解题的关键．7．北京有许多高校，下面四所高校校徽主体图案是轴对称图形的有（ ）A ．1个B ．2个C ．3个D ．4个B解析：B【分析】 根据轴对称图形的概念对各图案逐一进行判断即可得答案．【详解】第一个图案是轴对称图形，第二个图案不是轴对称图形，第三个图案是轴对称图形，第四个图案不是轴对称图形，综上所述：是轴对称图形的图案有2个，故选：B ．【点睛】本题考查轴对称图形，判断轴对称图形的关键是寻找对称轴，图形沿对称轴折叠，对称轴两边的图形能够完全重合；熟练掌握轴对称图形的定义是解题关键．8．如图，已知等腰三角形ABC 中，AB AC =，15DBC ∠=︒，分别以A 、B 两点为圆心，以大于12AB 的长为半径画圆弧，两弧分别交于点E 、F ，直线EF 与AC 相交于点D ，则A ∠的度数是（ ）A ．50°B ．60°C ．75°D ．45°A解析：A【分析】 根据中垂线的性质可得DA=DB ，设∠A=x ，则∠ABD=x ，结合等腰三角形的性质以及三角形内角和定理，列出方程，即可求解．【详解】又作图可知：EF 是AB 的垂直平分线，∴DA=DB ，∴∠A=∠ABD ，设∠A=x ，则∠ABD=x ，∵15DBC ∠=︒，∴∠ABC=x+15°，∵AB=AC ，∴∠C=∠ABC=x+15°，∴2(x+15°)+x=180°，∴x=50°，故选A ．【点睛】本题主要考查等腰三角形的性质，中垂线的性质以及三角形内角和定理，掌握中垂线的性质定理以及方程思想，是解题的关键．9．如图，在锐角ABC 中，AB AC =，D ，E 是ABC 内的两点，AD 平分BAC ∠，60EBC E ∠=∠=，若6BE cm =，2DE cm =，则BC 的长度是（ ）A ．6cmB ．6.5cmC ．7cmD ．8cm D解析：D【分析】延长ED 交BC 于点M ，延长AD 交BC 于点N ，过点D 作//DF BC 交BE 于点F ，根据等腰三角形的性质得出AN BC ⊥，BN CN =，根据60EBC E ∠=∠=，得出EBM △是等边三角形，进而得到6EB EM BM cm ===，通过//DF BC ，证明EFD △是等边三角形，进而得到2EF FD ED cm ===，所以求出4DM cm =，根据直角三角形的性质得到MN 的长度，从而得出BN 的长度，最后求出BC 的长度．【详解】延长ED 交BC 于点M ，延长AD 交BC 于点N ，过点D 作//DF BC 交BE 于点F ，如图，AB AC =，AD 平分BAC ∠，∴AN BC ⊥，BN CN =，∴90ANB ANC ∠=∠=，60EBC E ∠=∠=，∴EBM △是等边三角形，6BE cm =，∴6EB EM BM cm ===，//DF BC ，∴60EFD EBM ∠=∠=，∴EFD △是等边三角形，2DE cm =，∴2EF FD ED cm ===，∴4DM cm =，EBM △是等边三角形，∴60EMB ∠=，∴30NDM ∠=，∴2NM cm =，∴4BN BM NM cm =-=，∴28BC BN cm ==．故选：D ．【点睛】本题考查了等腰三角形的性质和等边三角形的性质，直角三角形中30角所对的直角边是斜边长的一半，求出MN 的长度是解决问题的关键．10．等腰三角形腰上的高与另一腰的夹角为30，则底角度数是（ ）A ．30B ．60︒C ．40︒或50︒D ．30或60︒D解析：D【分析】由三角形的高可在三角形的内部，也可在三角形的外部，所以分锐角三角形和钝角三角形两种情况作出符合题意的图形，再结合等腰三角形的性质与三角形的内角和定理求解即可．【详解】解：如图，分两种情况：①如图，当三角形的高在三角形的内部时，AB=AC ，BD ⊥AC ，∠ABD=30°，∴∠A=60°，∴∠C=∠ABC=1802A ︒-∠ =60°； ②如图，当三角形的高在三角形的外部时，AB=AC ，BD ⊥AC ，∠ABD=30°， ∴∠DAB=60°，∠BAC=120°，∴∠C=∠ABC=180302BAC ︒-∠=︒． 故选：D ．【点睛】本题考查了等腰三角形的性质和直角三角形的两锐角互余，三角形的内角和定理的应用，三角形的高的含义，分类讨论的数学思想，掌握分类讨论解决问题是解题的关键． 二、填空题11．如图，在平面直角坐标系中，直线l 与x 轴交于点1B ，与y 轴交点于D ，且111,60OB ODB =∠=︒，以1OB 为边长作等边三角形11AOB ，过点1A 作12A B 平行于x 轴，交直线l 于点2B ，以12A B 为边长作等边三角形212A A B ，过点2A 作23A B 平行于x 轴，交直线l 于点3B ，以23A B 为边长作等边三角形323A A B ，…，按此规律进行下去，则点6A 的横坐标是______．5【分析】过A1作A1A⊥OB1于A过A2作A2B⊥A1B2于B过A3作A3C⊥A2B3于C根据等边三角形的性质以及含30°角的直角三角形的性质分别求得A1的横坐标为A2的横坐标为A3的横坐标为进而解析：5【分析】过A1作A1A⊥OB1于A，过A2作A2B⊥A1B2于B，过A3作A3C⊥A2B3于C，根据等边三角形的性质以及含30°角的直角三角形的性质，分别求得A1的横坐标为1212-，，A2的横坐标为2212-，A3的横坐标为3212-，进而得到A n的横坐标为212n-，据此可得点A6的横坐标．【详解】解：如图所示,过A1作A1A⊥OB1于A,则OA=12OB1=12，即A1的横坐标为12=1212-，∵160ODB∠=°，∴∠OB1D=30°，∵A 1B 2//x 轴，∴∠A 1B 2B 1=∠OB 1D =30°，∠B 2A 1B 1=∠A 1B 1O =60°，∴∠A 1B 1B 2=90°，∴A 1B 2=2A 1B 1=2，过A 2作A 2B ⊥A 1B 2于B ,则A 1B =12A 1B 2=1， 即A 2的横坐标为12+1=2212-， 过A 3作A 3C ⊥A 2B 3于C ，同理可得,A 2B 3=2A 2B 2=4,A 2C =12A 2B 3=2， 即A 3的横坐标为12+1+2=3212-， 同理可得,A 4的横坐标为12+1+2+4=4212-， 由此可得,A n 的横坐标为212n -， ∴点A 6的横坐标是62163==31.522-， 故答案为31.5．【点睛】本题是一道找规律问题，涉及到等边三角形的性质、含30度角的直角三角形，解题的关键要利用等边三角形的性质总结出关于点A 的系列点的规律．12．如图，在ABC ∆中，CD 平分,ACB ∠点,E F 分别是,CD AC 上的动点．若6,12,ABC BC S ∆==则AE EF +的最小值是______________．【分析】作A 关于CD 的对称点H 由CD 是△ABC 的角平分线得到点H 一定在BC 上过H 作HF ⊥AC 于F 交CD 于E 连接AE 则此时AE ＋EF 的值最小AE ＋EF 的最小值＝HF 过A 作AG ⊥BC 于G 根据垂直平分线的解析：4【分析】作A 关于CD 的对称点H ，由CD 是△ABC 的角平分线，得到点H 一定在BC 上，过H 作HF ⊥AC 于F ，交CD 于E ，连接AE ，则此时，AE ＋EF 的值最小，AE ＋EF 的最小值＝HF ，过A 作AG ⊥BC 于G ，根据垂直平分线的性质和三角形的面积即可得到结论．【详解】作A 关于CD 的对称点H ，∵CD 是△ABC 的角平分线，∴点H 一定在BC 上，过H 作HF ⊥AC 于F ，交CD 于E ，连接AE ，则此时，AE ＋EF 的值最小，AE ＋EF 的最小值＝HF ，过A 作AG ⊥BC 于G ，∵△ABC 的面积为12，BC 长为6，∴AG ＝4，∵CD 垂直平分AH ，∴AC ＝CH ，∴S △ACH ＝12AC•HF ＝12CH•AG ， ∴HF ＝AG ＝4，∴AE ＋EF 的最小值是4，故答案是：4．【点睛】本题考查了轴对称−最短路线问题，解题的关键是正确的作出对称点和利用垂直平分线的性质证明AE ＋EF 的最小值为三角形某一边上的高线．13．如图，在ABC ∆中，31C ∠=︒，ABC ∠的平分线BD 交AC 于点D ，如果DE 垂直平分BC ，那么A ∠的度数为_______．【分析】根据垂直平分线和角平分线的性质求解即可；【详解】∵垂直平分∴∴∵∴∴∵BD 平分∴∴故答案是【点睛】本题主要考查了垂直平分线和角平分线的性质结合三角形外角性质和三角形内角和定理计算是关键解析：87︒【分析】根据垂直平分线和角平分线的性质求解即可；【详解】∵DE 垂直平分BC ，∴DB DC =，∴∠=∠DBC C ，∵31C ∠=︒，∴31DBC ∠=︒，∴62ADB C DBC ∠=∠+∠=︒，∵BD 平分ABC ∠，∴31ABD DBC ∠=∠=︒，∴180623187A ∠=︒-︒-︒=︒．故答案是87︒．【点睛】本题主要考查了垂直平分线和角平分线的性质，结合三角形外角性质和三角形内角和定理计算是关键．14．如图，在ABC 中，D 是BC 上一点，,105AC AD DB BAC ==∠=︒，则B ∠=________°．25【分析】设∠ADC ＝α然后根据AC ＝AD ＝DB ∠BAC ＝105°表示出∠B 和∠BAD 的度数最后根据三角形的内角和定理求出∠ADC 的度数进而求得∠B 的度数即可【详解】解：∵AC ＝AD ＝DB ∴∠B ＝ 解析：25【分析】设∠ADC ＝α，然后根据AC ＝AD ＝DB ，∠BAC ＝105°，表示出∠B 和∠BAD 的度数，最后根据三角形的内角和定理求出∠ADC 的度数，进而求得∠B 的度数即可．【详解】解：∵AC ＝AD ＝DB ，∴∠B ＝∠BAD ，∠ADC ＝∠C ，设∠ADC ＝α，∴∠B ＝∠BAD ＝2α ， ∵∠BAC ＝105°，∴∠DAC ＝105°﹣2α， 在△ADC 中， ∵∠ADC +∠C +∠DAC ＝180°，∴2α+105°﹣2α＝180°， 解得：α＝50°，∴∠B ＝∠BAD ＝2α＝25°， 故答案为：25．【点睛】 本题考查了等腰三角形的性质：①等腰三角形的两腰相等；②等腰三角形的两个底角相等，熟练掌握等腰三角形的性质是解题的关键．15．若一条长为24cm 的细线能围成一边长等于6cm 的等腰三角形，则该等腰三角形的腰长为__________cm ．【分析】分两种情况根据等腰三角形的性质及三角形的三边关系解答【详解】分两种情况：当6cm 的边为腰时底边长=24-6-6=12（cm ）∵6+6=12故不能构成三角形；当6cm 的边为底边时腰长=（cm ）解析：9【分析】分两种情况，根据等腰三角形的性质及三角形的三边关系解答．【详解】分两种情况：当6cm 的边为腰时，底边长=24-6-6=12（cm ），∵6+6=12，故不能构成三角形； 当6cm 的边为底边时，腰长=1(246)92⨯-=（cm ），由于6+9>9，故能构成三角形， 故答案为：9．【点睛】此题考查等腰三角形的性质：两腰相等，依据三角形三边关系，解题中运用分类思想解答．16．若点P(x-y ，y)与点Q(-1，-5)关于x 轴对称，则x+y=______．9【分析】根据关于x 轴对称的点横坐标相同纵坐标互为相反数可得答案【详解】由点P （x-yy ）与点Q （-1-5）关于x 轴对称得x-y ＝-1y ＝5解得x ＝4y ＝5x+y=4+5=9故答案为：9【点睛】本题解析：9【分析】根据关于x 轴对称的点，横坐标相同，纵坐标互为相反数，可得答案．【详解】由点P （x-y ，y ）与点Q （-1，-5）关于x 轴对称，得x-y ＝-1，y ＝5．解得x ＝4，y ＝5，x+y=4+5=9，故答案为：9【点睛】本题考查了关于x 轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：关于x 轴对称的点，横坐标相同，纵坐标互为相反数；关于y 轴对称的点，纵坐标相同，横坐标互为相反数；关于原点对称的点，横坐标与纵坐标都互为相反数．17．如图所示的网格是正方形网格，点A，B，C，D，O是网格线交点，那么∠___________CODAOB∠（填“＞”，“＜”或“＝”）．>【分析】如图过点B作BE⊥AC于E证明△BOE是等腰直角三角形得到∠BOE=过点C作CF⊥OC使FC=OC证明△OCF是等腰直角三角形得到∠FOC=由图知∠FOC>∠COD即可得到∠AOB>∠CO解析：>【分析】如图，过点B作BE⊥AC于E，证明△BOE是等腰直角三角形，得到∠BOE=45︒，过点C 作CF⊥OC，使FC=OC，证明△OCF是等腰直角三角形，得到∠FOC=45︒，由图知∠FOC>∠COD，即可得到∠AOB>∠COD．【详解】如图，过点B作BE⊥AC于E，∵OB=OE=2，∠BEO=90︒，∴△BOE是等腰直角三角形，∴∠BOE=45︒，过点C作CF⊥OC，使FC=OC，∴∠FCO=90︒，∴△OCF是等腰直角三角形，∴∠FOC=45︒，由图知∠FOC>∠COD，∴∠AOB>∠COD，故答案为：>．．【点睛】此题考查等腰直角三角形的判定及性质,角的大小比较，根据图形确定角的位置关系是解题的关键．18．如图，∠AOB＝45°，OC平分∠AOB，点M为OB上一定点，P为OC上的一动点，N 为OB上一动点，当PM＋PN最小时，则∠PMO的度数为___________．45°【分析】找到点M 关于OC 对称点M′过点M′作M′N ⊥OB 于点N 交OC 于点P 则此时PM+PN 的值最小再根据角平分线的性质及三角形内角和即可得出答案【详解】解：如图找到点M 关于OC 对称点M′过点M解析：45°【分析】找到点M 关于OC 对称点M′，过点M′作M′N ⊥OB 于点N ，交OC 于点P ，则此时PM+PN 的值最小，再根据角平分线的性质及三角形内角和即可得出答案．【详解】解：如图，找到点M 关于OC 对称点M′，过点M′作M′N ⊥OB 于点N ，交OC 于点P ，则此时PM+PN 的值最小．∵PM=PM′，∴此时PM+PN=PM′+PN′=M′N′，∵点M 与点M′关于OC 对称，OC 平分∠AOB ，∴OM=OM′，∵∠AOB=45°，∴∠PM'O=∠AOB=45°，∴∠PMO=∠PM'O=45°，故答案为：45°．【点睛】本题考查了利用轴对称的知识寻找最短路径的知识，涉及到两点之间线段最短、垂线段最短的知识，有一定难度，正确确定点P 及点N 的位置是关键．19．如图，25AOB ∠=︒，点M ，N 分别是边OA ，OB 上的定点，点P ，Q 分别是边OB ，OA 上的动点，记MPQ α∠=，PQN β∠=，当MP PQ QN ++的值最小时，βα-的大小=__________（度）．50【分析】作M 关于OB 的对称点N 关于OA 的对称点连接交OB 于点P 交OA 于点Q 连接MPQN 可知此时最小此时再根据三角形外角的性质和平角的定义即可得出结论【详解】作M 关于OB 的对称点N 关于OA 的对称点解析：50【分析】作M 关于OB 的对称点M '，N 关于OA 的对称点N '，连接M N ''，交OB 于点P ，交OA 于点Q ，连接MP ，QN ，可知此时MP PQ QN ++最小，此时OPM OPM NPQ OQP AQN AQN ''∠=∠=∠∠=∠=∠，，再根据三角形外角的性质和平角的定义即可得出结论．【详解】作M 关于OB 的对称点M '，N 关于OA 的对称点N '，连接M N ''，交OB 于点P ，交OA 于点Q ，连接MP ，QN ，如图所示．根据两点之间，线段最短，可知此时MP PQ QN++最小，即MP PQ QN M N ''++=， ∴OPM OPM NPQ OQP AQN AQN ''∠=∠=∠∠=∠=∠，，∵MPQ PQN αβ∠=∠=，， ∴11(180)(180)22QPN OQP αβ∠=︒-∠=︒-，， ∵QPN AOB OQP ∠=∠+∠，25AOB ∠=︒， ∴11(180)25(180)22αβ︒-=︒+︒- ， ∴50βα-=︒ ． 故答案为：50．【点睛】本题考查轴对称-最短问题、三角形内角和，三角形外角的性质等知识，灵活运用所学知识解决问题是解题的关键，综合性较强．20．如图，ABC ∆中，ABC ∠与ACB ∠的平分线交于点F ，过点F 作//DE BC 交AB 于点D ，交AC 于点E ，那么下列结论：①BDF ∆和CEF ∆都是等腰三角形；②DE BD CE =+；③ADE ∆的周长等于AB 与AC 的和；④BF CF =；⑤若80A ∠=︒，则130BFC ∠=︒．其中正确的有_______．（填正确的序号）．①②③⑤【分析】①根据平行线性质和角平分线定义可以得到DB=DFEF=EC 从而得到△BDF 和△CEF 都是等腰三角形；②同①有DB=DFEF=EC 所以DE=DF+EF=BD+CE ；③由②得：△ADE 的解析：①②③⑤【分析】①根据平行线性质和角平分线定义可以得到DB=DF ，EF=EC ，从而得到△BDF 和△CEF 都是等腰三角形；②同①有DB=DF ，EF=EC ，所以DE=DF+EF=BD+CE ；③由②得：△ADE 的周长为：AD+DE+AE=AB+BD+CE+AE=AB+AC ；④因为∠ABC 不一定等于∠ACB ，所以∠FBC 不一定等于∠FCB ，所以BF 与CF 不一定相等；⑤由角平分线定义和三角形内角和定理可以得解．【详解】解：∵DE ∥BC ，∴∠DFB=∠FBC ，∠EFC=∠FCB ，∵△ABC 中，∠ABC 与∠ACB 的平分线交于点F ，∴∠DBF=∠FBC ，∠ECF=∠FCB ，∴∠DBF=∠DFB ，∠ECF=∠EFC ，∴DB=DF ，EF=EC ，即△BDF 和△CEF 都是等腰三角形；故①正确；∴DE=DF+EF=BD+CE ，故②正确；∴△ADE 的周长为：AD+DE+AE=AB+BD+CE+AE=AB+AC ；故③正确；∵∠ABC 不一定等于∠ACB ，∴∠FBC 不一定等于∠FCB ，∴BF 与CF 不一定相等，故④错误； 由题意知，1122FBC ABC FCB ACB ∠=∠∠=∠，， ∴()()11801802BFC FBC FCB ABC ACB ∠=︒-∠+∠=︒-∠+∠ =()()111801801801808022A ︒-︒-∠=︒-︒-︒ =130°,故⑤正确，故答案为①②③⑤．【点睛】 本题考查了等腰三角形的判定和性质、角平分线的性质、平行线的性质及三角形的内角和定理；题目利用了两直线平行，内错角相等及等角对等边来判定等腰三角形；等量代换的利用是解答本题的关键．三、解答题21．如图，点E 在ABC 的边AB 上，90ABC EAD ∠=∠=︒，30BAC ADE ∠=∠=︒，DE 的延长线交AC 于点G ，交BC 延长线于点F ．AB=AD ，BH ⊥DF ，垂足为H ．（1）求HAE ∠的度数；（2）求证：DH FB FH =+．解析：（1）=15∠HAE ；（2）见解析【分析】（1）连接BG ，先根据等腰三角形的判定得出AG=AD ，再根据SSS 得出△AGH ≌△ABH ，从而得出=∠∠HAE HAG ，继而得出HAE ∠的度数；（2）在DH 上取HM=HF ，连接BM ，根据垂直平分线的性质得出BF=BM ，再根据等腰三角形的判定得出DM=BM ，从而得出结论【详解】解：（1）连接BG∵90EAD ∠=︒，30BAC ∠=︒，∴∠DAG=120°，∵30ADE ∠=︒，∴30∠=∠=︒ADE AGD ，∴AG=AD ，∵AB=AD ，∴AG=AB ，∵30BAC ∠=︒，∴75∠=∠=︒AGB ABG ，∵BH ⊥DF ，90EAD ∠=︒，∴=90∠∠=︒BHE EAD ，∵=∠∠BEH AED ，∴30∠=∠=︒ADE EBH ，∴45∠=∠-∠=︒HBG ABG EBH ，∵90FHB ∠=︒，∴∠=∠HBG HGB ，∴GH=BH ，∵AG=AB ，AH=AH ，∴△AGH ≌△ABH ，∴=∠∠HAE HAG ，∵30BAC ∠=︒，∴=15∠HAE ；（2）在DH 上取HM=HF ，连接BM ；∵90ABC EAD ∠=∠=︒，∴AD//BF ，∴30∠=∠=︒F ADE ，∵BH ⊥DF ，HM=HF ，∴BF=BM∴30∠=∠=︒F BMF∵AB=AD ，90EAD ∠=︒∴45ADB ∠=︒，∵30ADE ∠=︒∴15∠=︒MDB ，∵30∠=︒=∠+∠BMF MBD MDB ，∴==15∠∠MBD MDB ，∴BM=DM=BF ，∵DH=DM+HM ，∴DH=FH+BF【点睛】本题考查了等腰三角形的性质和判定、全等三角形的性质和判定、垂直平分线的性质，解题的关键是学会添加常用辅助线面构造全等三角形解决问题，属于中考常考题型． 22．如图，ABC 是边长为10的等边三角形，现有两点P 、Q 沿如图所示的方向分别从点A 、点B 同时出发，沿ABC 的边运动，已知点P 的速度为每秒1个单位长度，点Q 的运度为每秒2个单位长度，当点P 第一次到达B 点时，P 、Q 同时停止运动． （1）点P 、Q 运动几秒后，可得到等边三角形APQ ？（2）点P 、Q 运动几秒后，P 、Q 两点重合？（3）当点P 、Q 在BC 边上运动时，能否得到以PQ 为底边的等腰APQ ？如存在，请求出此时P 、Q 运动的时间．解析：（1）点P 、Q 运动103秒后，可得到等边三角形APQ ；（2）点P 、Q 运动10秒后，P 、Q 两点重合；（3）当点P 、Q 在BC 边上运动时，能得到以PQ 为底边的等腰三角形，此时P 、Q 运动的时间为403秒． 【分析】（1）设点P 、Q 运动t 秒后，可得到等边三角形APQ ，利用,AP AQ = 列方程，解方程可得答案；（2）设点P 、Q 运动x 秒后，P 、Q 两点重合，由追及问题中的相等关系：Q 的运动路程等于P 的运动路程加上相距的路程，列方程，解方程即可得到答案；（3）当点P 、Q 在BC 边上运动时，可以得到以PQ 为底边的等腰三角形．先证明：ACP △≌ABQ △，可得CP BQ =，再列方程，解方程并检验即可得到答案．【详解】解：（1）设点P 、Q 运动t 秒后，可得到等边三角形APQ ，如图①，AP t =，102AQ AB BQ t =-=-，∵三角形APQ 是等边三角形，,AP AQ ∴=∴102t t =-，解得103t =， ∴点P 、Q 运动103秒后，可得到等边三角形APQ ．（2）设点P 、Q 运动x 秒后，P 、Q 两点重合，102x x +=，解得：10x =．∴点P 、Q 运动10秒后，P 、Q 两点重合．（3）当点P 、Q 在BC 边上运动时，可以得到以PQ 为底边的等腰三角形．理由如下： 由（2）知10秒时P 、Q 两点重合，恰好在C 处，如图②，假设APQ 是等腰三角形，∴AP AQ =，∴APQ AQP ∠=∠，∴APC AQB ∠=∠，∵ACB △是等边三角形，∴C B ∠=∠，在ACP △和ABQ △中，,,,AC AB C B APC AQB =⎧⎪∠=∠⎨⎪∠=∠⎩， ∴ACP △≌ABQ △，∴CP BQ =，设当点P 、Q 在BC 边上运动时，P 、Q 运动的时间y 秒时，APQ 是等腰三角形， 由题意得：10CP y =-，302QB y =-，∴ 10302y y -=-， 解得：403y =， P 的最长运动时间为2020,1s = Q 从B A C B →→→的最长时间为30=152s ， 由403＜15， ∴ 403y =符合题意， ∴当点P 、Q 在BC 边上运动时，能得到以PQ 为底边的等腰三角形，此时P 、Q 运动的时间为403秒． 【点睛】 本题考查的是三角形全等的判定与性质，等腰三角形的判定与性质，等边三角形的判定与性质，动点问题，掌握以上知识是解题的关键．23．已知AOB ∠及一点P ，利用直尺和圆规，根据下列要求作图（保留作图痕迹，不要求写作法）（1）过点P 作OA 、OB 的垂线，垂足分别为点M 、N ；（2）猜想MPN ∠与AOB ∠之间的数量关系，并说明理由．解析：（1）见解析；（2）∠MPN+∠AOB=180°或∠MPN=∠AOB，理由见解析【分析】（1）根据垂线的定义画出图形即可解决问题；（2）根据四边形内角和为360°或“8字型”的性质即可解决问题；【详解】（1）过点P作OA、OB的垂线PM、PN如图所示；（2）猜想：∠MPN+∠AOB=180°或∠MPN=∠AOB．理由：左图中，在四边形PMON中，∵∠PMO=∠PNO=90°，∴∠MPN+∠AOB=180°．右图中，∵∠PJM=∠OJN，∠PMJ=∠JNO=90°，∴∠MPN=∠AOB．【点睛】本题考查了作图-基本作图，解题的关键是熟练掌握基本知识，属于中考常考题型．24．在等边三角形ABC中，点E为线段AB上一动点，点E与A，B不重合，点D在CB的延长线上，且ED＝EC．（1）当E为边AB的中点时，如图1所示，确定线段AE与BD的大小关系，并证明你的结论；（2）如图2，当E不是边AB的中点时，（1）中的结论是否成立？若不成立，请直接写出EF BC交AC于点F）BD与AE的数量关系；若成立，请给予证明；（提示：过E作//（3）在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED＝EC，ABC 的边长为1，AE＝2，请直接写出CD的长．解析：（1）AE＝BD；见解析；（2）成立；AE＝BD；见解析；（3）CD的长为3或1.【分析】（1）根据等边三角形三线合一的性质证得∠ECB＝30°，由DE＝CE，求出∠D＝∠ECB＝30°得到∠DEB＝30°，推出BD＝BE，根据AE＝BE证得结论；（2）过E作EF∥BC交AC于点F，得到△AEF是等边三角形，推出BE=CF，利用∠DBE＝∠EFC＝120°，∠BED＝∠ECF，证得△DEB≌△ECF（AAS），得到BD＝EF=AE；（3）作EF∥BC交CA的延长线于点F，则△AEF为等边三角形，利用∠CEF＝∠EDB，EB＝CF＝3，∠F＝∠B＝60°，证得△CEF≌△EDB（AAS），得到BD＝EF＝2，求出CD＝BD－BC ＝1，同理可得CD＝3【详解】解：（1）AE＝BD；证明：∵△ABC为等边三角形，AE＝BE，∴CE平分∠ACB，∴∠ECB＝30°．∵DE＝CE，∴∠D＝∠ECB＝30°．∵∠ABC＝∠D＋∠DEB＝60°，∴∠DEB＝30°，∴∠D＝∠DEB，∴BD＝BE．∵AE＝BE，∴AE＝BD；（2）当E为边AB上任意一点时，AE＝BD仍成立；证明：如图1，过E作EF∥BC交AC于点F．∵△ABC是等边三角形，∴∠ABC＝∠ACB＝∠A＝60°，AB＝AC＝BC，∴∠AEF＝∠ABC＝60°，∠AFE＝∠ACB＝60°，即∠AEF＝∠AFE＝∠A＝60°,∴△AEF是等边三角形，∴AE＝EF＝AF．∵∠ABC＝∠ACB＝60°，∴∠DBE＝∠EFC＝120°，∠D＋∠BED＝∠FCE＋∠ECD＝60°．∵DE ＝EC ，∴∠D ＝∠ECD ，∴∠BED ＝∠ECF ，∴△DEB ≌△ECF （AAS ），∴BD ＝EF ，∴AE ＝BD ；（3）CD 的长为3或1如图2，作EF ∥BC 交CA 的延长线于点F ，则△AEF 为等边三角形，∴AF ＝AE ＝EF ＝2，∠BEF ＝60°，∴∠CEF ＝60°＋∠BEC ．∵∠EDC ＝∠ECD ＝∠B ＋∠BEC ＝60°＋∠BEC ，∴∠CEF ＝∠EDB ．又∵EB ＝CF ＝3，∠F ＝∠B ＝60°，∴△CEF ≌△EDB （AAS ），∴BD ＝EF ＝2，∴CD ＝BD －BC ＝1，如图3，同理可得CD ＝3，综上所述，CD 的长为3或1【点睛】此题考查等边三角形的性质，全等三角形的判定及性质，平行线的性质，等腰三角形等边对等角的性质，熟练掌握三角形的知识并熟练应用是解题的关键．25．如图，在Rt ABC △中，90ACB ∠=︒，CA CB =，M 是AB 的中点，点D 在BM 上，AE CD ⊥，BF CD ⊥，垂足分别为E ，F ，连接EM ．（1）求证：CE BF =；（2）求证：AEM DEM ∠=∠．解析：（1）证明见解析；（2）证明见解析【分析】（1）先证明CAE BCF ∠=∠，再证明CAE BCF ≌△△，从而可得结论；（2）连接CM ，FM ，先证明ECM FBM ∠=∠，再证明CME BMF ≌△△，可得EM FM =，EMC FMB ∠=∠，再证明FME 是等腰直角三角形，可得45MED ∠=︒，从而可得结论．【详解】证明：（1）AE CD ⊥，BF CD ⊥，90AEC CFB ∴∠=∠=︒．90ACB ∠=︒，90BCF ACE ACE EAC ∴∠+∠=︒=∠+∠CAE BCF ∴∠=∠．CA BC =． ()CAE BCF AAS ∴≌△△．CE BF ∴=．（2）连接CM ，FM在Rt ABC △中，CA CB =，点M 是AB 的中点，90,ACB ∠=︒BM AM ∴=，CM AB ⊥，CM 平分ACB ∠，45ACM BCM CBM CAM ∴∠=∠=∠=∠=︒，CM BM AM ==，由CAE BCF ≌△△可得：ACE CBF ∠=∠．,ACM ECM CBM MBF ∴∠+∠=∠+∠ECM FBM ∴∠=∠．又CE BF =，()CME BMF SAS ∴≌△△．EM FM ∴=，EMC FMB ∠=∠．90EMF FMB DME CME DME ∠=∠+∠=∠+∠=︒．FME ∴△是等腰直角三角形．45MED ∴∠=︒，90AED ∠=︒，45AEM DEM ∴∠=∠=︒．【点睛】本题考查的的三角形全等的判定与性质，等腰直角三角形的判定与性质，掌握以上知识是解题的关键．26．如图，在所给平面直角坐标系（每小格均为边长是1个单位长度的正方形）中完成下列各题．（1）已知()6,0A -，()2,0B -，()4,2C -，画出ABC 关于y 轴对称的图形△111A B C △，并写出1B 的坐标；（2）在y 轴上画出点P ，使PA PC +最小；（3）在（1）的条件下，在y 轴上画出点M ，使11MB MC -最大．解析：（1）见解析；B 1（2，0）；（2）见解析；（3）见解析【分析】（1）先作出点A 、B 、C 关于y 轴的对称点A 1、B 1、C 1，顺次连结，则△111A B C △为所求，点()2,0B -，关于y 轴对称，横坐标符号改变B 1（2，0）； （2）连结AC 1，交y 轴于点P ，两用两点之交线段最短知AC 1最短即可；（3）延长C 1B 1交y 轴于M ，利用两边之差小于第三边即可．【详解】解：（1）先作出点A 、B 、C 关于y 轴的对称点A 1、B 1、C 1，顺次连结，则△111A B C △为所求，点()2,0B -，关于y 轴对称，横坐标符号改变B 1（2，0），如图；B 1（2，0）；（2）连结AC 1，交y 轴于点P ，两用两点之交线段最短知AC 1最短，则PA+PC=PA+PC 1=AC 1，则点P 为所求，如图；（3）延长C 1B 1交y 轴于M ，利用两边之差小于第三边，11MB MC -最大=C 1B 1，如图．【点睛】 本题考查轴对称作图，线段公里，三角形三边关系，掌握轴对称作图，线段公里，三角形三边关系是解题关键．27．如图，点A ，C ，D ，B 四点共线，且AC BD =，A B ∠=∠，ADE BCF ∠=∠．（1）求证：ADE BCF ≌；（2）若9DE =，CG 4=，求线段EG 的长．解析：（1）证明见解析；（2）5EG =．【分析】（1）根据AC=BD 可得AD=BC ，然后利用已知条件根据ASA 即可证明全等；（2）根据（1）中的全等可得∠ADE=∠BCF ，再结合等角对等边可得4DG CG ==，最后利用线段的和差即可求得EG 的长度．【详解】解：（1）证明：∵AC=BD ，∴AC+CD=BD+CD ，∴AD=BC ，在△ADE 和△BCF 中，A B AD BCADE BCF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADE ≌△BCF （ASA ）；（2）∵△ADE ≌△BCF ，∴∠ADE=∠BCF ，∴4DG CG ==，∵9DE =，∴5EG DE DG =-=．【点睛】本题考查全等三角形的性质和判定，等腰三角形等角对等边．熟练掌握全等三角形的几种判定定理，并能结合题中所给条件灵活运用是解题关键．28．已知ABC 是等边三角形，点D 是AC 的中点，点P 在射线BC 上，点Q 在线段AB 上，120PDQ ∠=︒．（1）如图1，若点Q 与点B 重合，求证：DB DP =；（2）如图2，若点P 在线段BC 上，8AC =，求AQ PC +的值．解析：（1）证明见解析；（2）4．【分析】（1）由等边三角形的性质证明30DBC ∠=︒，再利用三角形的内角和定理求解30DPB ∠=︒，从而可得结论； （2）过点D 作//DE BC 交AB 于点E ，先证明ADE 为等边三角形，再证明QDE PDC ≌，可得QE PC =， 从而可得答案．【详解】证明：（1）∵ABC 为等边三角形，∴,60BA BC ABC =∠=︒∵D 为AC 的中点，∴DB 平分ABC ∠，∴30DBC ∠=︒． ∵120PDB ∠=︒，∴1801203030DPB ∠=︒-︒-︒=︒，∴DBC DPB ∠=∠，∴DB DP =．（2）过点D 作//DE BC 交AB 于点E ．∵ABC 为等边三角形，8AC =，点D 是AC 的中点，∴4,60AD CD ABC ACB A ==∠=∠=∠=︒．∵//DE BC ，∴60AED B ∠=∠=︒．60ADE C ∠=∠=︒，∴ADE 为等边三角形，120EDC ∠=︒，∴4AD ED AE ===，。

最新Word 欢送下载
轴对称
一．知识框架
二．知识概念
1.对称轴：如果一个图形沿某条直线折叠后，直线两旁的局部能够互相重合，那么这个图形叫做轴对称图形；这条直线叫做对称轴。

2.性质：〔1〕轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

〔2〕角平分线上的点到角两边距离相等。

〔3〕线段垂直平分线上的任意一点到线段两个端点的距离相等。

〔4〕与一条线段两个端点距离相等的点，在这条线段的垂直平分线上。

〔5〕轴对称图形上对应线段相等、对应角相等。

3.等腰三角形的性质：等腰三角形的两个底角相等，〔等边对等角〕
4.等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合，简称为“三线合一〞。

5.等腰三角形的判定：等角对等边。

6.等边三角形角的特点：三个内角相等，等于60°，
7.等边三角形的判定：三个角都相等的三角形是等腰三角形。

有一个角是60°的等腰三角形是等边三角形
有两个角是60°的三角形是等边三角形。

8.直角三角形中，30°角所对的直角边等于斜边的一半。

9．直角三角形斜边上的中线等于斜边的一半。

本章内容要求学生在建立在轴对称概念的根底上，能够对生活中的图形进行分析鉴赏，亲身经历数学美，正确理解等腰三角形、等边三角形等的性质和判定，并利用这些性质来解决一些数学问题。

第十三章 轴对称知识点总结及常见题型1、轴对称图形：一个图形沿一条直线对折，直线两旁的部分能够完全重合。

这条直线叫做对称轴。

互相重合的点叫做对应点。

2、轴对称：两个图形沿一条直线对折，其中一个图形能够与另一个图形完全重合。

这条直线叫做对称轴。

互相重合的点叫做对应点。

3、轴对称图形与轴对称的区别与联系：（1）区别：轴对称图形讨论的是“一个图形与一条直线的对称关系” ；轴对称讨论的是“两个图形与一条直线的对称关系”。

（2）联系：把轴对称图形中“对称轴两旁的部分看作两个图形”便是轴对称；把轴对称的“两个图形看作一个整体”便是轴对称图形。

4、轴对称的性质：（1）成轴对称的两个图形全等。

（2）对称轴与连结“对应点的线段”垂直。

（3）对应点到对称轴的距离相等。

（4）对应点的连线互相平行。

5、线段的垂直平分线：（1）定义：经过线段的中点且与线段垂直的直线，叫做线段的垂直平分线。

如图2，∵CA=CB ，直线m ⊥AB 于C ，∴直线m 是线段AB 的垂直平分线。

（2）性质：线段垂直平分线上的点与线段两端点的距离相等。

如图3，∵CA=CB ，直线m ⊥AB 于C ，点P 是直线m 上的点。

∴PA=PB 。

（3）判定：与线段两端点距离相等的点在线段的垂直平分线上。

如图3，∵PA=PB ，直线m 是线段AB 的垂直平分线，∴点P 在直线m 上 。

6、等腰三角形：（1）定义：有两条边相等的三角形，叫做等腰三角形。

①相等的两条边叫做腰。

第三条边叫做底。

②两腰的夹角叫做顶角。

③腰与底的夹角叫做底角。

说明：底角顶角⨯-=2180顶角顶角底角21-902180︒=-︒=可见，底角只能是锐角。

（2）性质：①等腰三角形是轴对称图形，其对称轴是“底边的垂直平分线”，只有一条。

②“等边对等角”：等腰三角形的两个底角相等。

如图5，在△ABC 中 ∵AB=AC∴∠B=∠C 。

③三线合一：顶角平分线、底边上的中线和底边上的高相互重合。