第五章 稳恒磁场3节
- 格式:doc
- 大小:1.17 MB
- 文档页数:6





第五章 稳恒磁场设0x <的半空间充满磁导率为μ的均匀介质,0x >的半空间为真空,今有线电流沿z 轴方向流动,求磁感应强度和磁化电流分布。
解:如图所示令 110A I H e r = 220A IH e r= 由稳恒磁场的边界条件知,12t t H H = 12n n B B = 又 B μ= 且 n H H =所以 1122H H μμ= (1) 再根据安培环路定律H dl I ⋅=⎰得 12IH H rπ+= (2) 联立(1),(2)两式便解得,21120I I H r rμμμμπμμπ=⋅=⋅++012120I I H r rμμμμπμμπ=⋅=⋅++ 故, 01110IB H e r θμμμμμπ==⋅+ 02220IB H e rθμμμμμπ==⋅+ 212()M a n M M n M =⨯-=⨯ 220()B n H μ=⨯-00()0In e rθμμμμπ-=⋅⋅⨯=+ 222()M M M J M H H χχ=∇⨯=∇⨯=∇⨯0000(0,0,)zJ Ie z μμμμδμμμμ--=⋅=⋅++ 半径为a 的无限长圆柱导体上有恒定电流J 均匀分布于截面上,试解矢势A 的微分方程,设导体的磁导率为0μ,导体外的磁导率为μ。
?解: 由电流分布的对称性可知,导体内矢势1A 和导体外矢势2A 均只有z e 分量,而与φ,z 无关。
由2A ∇的柱坐标系中的表达式可知,只有一个分量,即 210A J μ∇=- 220A ∇= 此即101()A r J r r r μ∂∂=-∂∂21()0A r r r r∂∂=∂∂ 通解为 21121ln 4A Jr b r b μ=-++212ln A c r c =+ 当0r =时,1A 有限,有10b =由于无限长圆柱导体上有恒定电流J 均匀分布于截面上,设r a =时, 120A A ==,得202121ln 04Ja b c a c μ-+=+=)又r a =时,12011e A e A ρρμμ⨯∇⨯=⨯∇⨯,得 112c Ja a μ-=所以 2221220111,,224c Ja c Ja b Ja μμμ=-=-=所以, 22101()4A J r a μ=--221ln 2a A Ja rμ=写成矢量形式为 22101()4A J r a μ=--221ln 2a A Ja rμ=设无限长圆柱体内电流分布,0()z J a rJ r a =-≤求矢量磁位A 和磁感应B 。

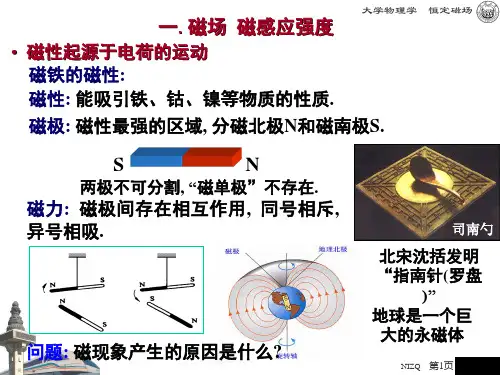
第五章稳恒磁场第一节磁场运动电荷的磁场1. 磁场磁现象的发现要比电现象早得多,公元前300 多年我国就发现了磁石吸铁现象,东汉时期就有了“司南”。
从1820 年开始,科学家逐步发现了磁和电的紧密关系:①磁铁有磁性,即有吸引铁、钻、镍等磁性物质的性质;②磁铁有磁极(磁性最强处),且恒有N 极和S极,磁极间有相互作用力,同性相斥,异性相吸;③运动电荷和电流对磁针有作用;④磁铁对运动电荷和电流也有作用;⑤运动电荷和电流与运动电荷和电流之间都有相互作用等。
由此而得,磁铁周围有磁场,运动电荷和电流周围也有磁场,它们之间的相互作用是通过磁场进行的,而非超距作用,安培磁性起源假设表明:一切磁现象的根源都是运动电荷(电流).2. 磁感应强度为了表征磁场的强弱及分布,引入物理量磁感应强度,用 B 表示,单位是特斯拉(T) , 1T= 1N-A-1•m-1。
关于B的定义有各种不同的方法,有的用电流在磁场中受的力来定义,有的用通电线圈在磁场中受的力矩来定义,为了更好地反映磁场的本质,且与电场强度E的定义相对应,我们定义:磁感应强度B为单位运动正电荷qv 在磁场中受到的最大力 F ,即F=q(v x B)实验证明磁场像电场一样,也满足叠加原理B 二刀B 或B = /dB第二节 电流的磁场 毕-萨定律1.电流的磁场电流周围有磁场,稳恒电流的磁场是稳恒磁场。
由于稳恒电 流总是闭合的,且形状各异,所以要想求得总磁场分布,必须先 研究一小段电流的磁场。
沿电流方向取一小段电流 I dl,称作电流元。
得出电流元产生磁场的规律:2d B =卩 o ldl x r/4 n r称作毕奥-萨伐尔定律,它表明一小段电流元产生的磁感应强度 dB 的大小,与电流元I dl 成正比,与电流元到场点距离r 的平方 成反比,且与I dl 和r 夹角的正弦成正比,其方向由右手螺旋法 则确定。
毕-萨定律可以从运动电荷的磁场公式中推得,而它也是一 个实验定律,虽然电流元不可能单独存在,但大量间接的实验都 证明了它的正确性。




§3 磁场的“高斯定理”与安培环路定理
引言:
磁场、电场均是矢量场,但磁场与电场性质不同。
在电学中有场方程:
⎰∑=⋅S
s q s d D 内
0ϖϖ, ⎰=⋅0l d E ϖ
ϖ
而在磁学中相应的该两方面(通量、环流)又该如何?即
⎰=⋅s
s d B ?ϖϖ, ?=⋅⎰L
l d B ϖ
ϖ
它们均可由毕奥-萨伐尔定律,结合叠加原理导出。
一、磁场的“高斯定理”
1、磁通量
引入磁力线形象化地描述磁场,疏密和切向所代表的含义类同电力线。
如图5-17,规定:通过一曲面S 的磁通量为
⎰
⎰=⋅=ΦS
S
m dS B S d B θcos ϖ
ϖ
在SI 制中各物理量的单位为
m Φ:韦伯(Wb ),1韦伯=1特21米⨯
B ρ
: 特斯拉(T ),2111米
韦伯特=,具有磁通密度概念。
2、B ρ
线的闭合性
即磁场的高斯定理:⎰=⋅S
S d B 0ϖ
ϖ。
表明:闭合曲面S 的磁通量为零,自然界
中不存在自由磁荷(磁单极)。
因稳恒电流本身是闭合的(⎰
=⋅S
S d j 0ϖ
ϖ)
,故闭合电流与闭合B ϖ
线相互套链。
高斯定理也表明,磁力线是无头无尾的闭合线,磁场是无源场。
图5-17 图5-18
θ B ϖ
d n ds s ϖ
ϖ=
Id l ϖθ r
d B ϖ
闭面S
3、高斯定理的证明思路
高斯定理可从毕奥-萨伐尔定律严格证明,这里仅提供思路。
如图5-18。
(1) 首先考虑单个电流元l Id ϖ
之场中
以l Id ϖ为轴线取一磁力线元管,其上磁场2
04sin r Idl dB πθμ=处处相等;再取任意闭曲面S ,若S 与之交链,则一进一出,0=Φm d ;若S 与之不交链,仍0=Φm d ;
再展扩至整体S 面上,得0=Φm 。
(2) 然后再考虑任意回路之总场是各电流元之场的叠加,因l Id ϖ
是任一电流
元,故对整体考虑,其结论不变。
二、安培环路定理
1、研究:⎰=⋅L
l d B ?ϖ
ϖ
2、特点:取积分回路L (称之为安培环路)沿B ϖ线,因B ϖ线闭合,且B ϖ
与l
d ϖ的夹角为零,而有⎰≠⋅L
l d B 0ϖ
ϖ。
3、内容:∑⎰=⋅)
(0内L L
I l d B μϖ
ϖ,其中右侧为穿过闭路L 的电流之代数和,按右
手定则规定,参见图5-19。
图5-19
4、定理证明:该定理可由毕奥-萨伐尔定律证明,下面先看l d B ρ
ρ⋅,再计算⎰⋅L
l d B ρ
ρ,最后再用叠加原理。
如图5-20,L -安培环路,L '-载流回路,作一负l d ρ
位移后成L ''。
I
I
L (正)
L (负) 右手定则 → →
图5-20
(1) 计算l d B ρ
ρ⋅
∵⎰
'
⨯'=
L r
r l d I B 2
04)ρπ
μ
∴l d r r
l d I l d B L ϖϖ
ϖϖ⋅⨯'=
⋅⎰')ˆ(42
0πμ ⎰'⋅'⨯=L r r
l d l d I 20ˆ)(4ϖ
ϖπμ (轮积) =⎰'⋅'-⨯L r r
l d l d I 20ˆ)(4ϖ
ϖπμ (换位)
如图5-20,s d l d l d ϖ
ϖϖ=-⨯)(,则
Ω-=-⋅-=⋅=⋅-⨯'d r r s d r r s d r r l d l d 2
22)
()()ϖ)ϖ)ϖϖ
为对P 点所张元立体角,从而
Ω-
=Ω-=⋅⎰
'
π
μπ
μ4400
I
d I l d B L ϖϖ Ω代表L '回路作位移l d ϖ
-所扫过带状面S 对P 点所张立体角。
S ″ L ″(后) S S ′
L ′(前)
I 载流回路L ′
r
ϖ P
d l ϖ
积分回路L
位移-d l ϖ
-r ˆ d s ϖ
-d l ϖ
再取以L '、L ''为周界(前后)之闭面:s s s '++'',使之不套链L (P 点在外),则0=Ω+Ω'-Ω'',即
l d l d l
ϖϖ
ϖ⋅Ω∇=⋅∂Ω∂=Ω'-Ω''=Ω-
代入上式给出
l d I
l d B ϖϖϖ⋅Ω∇=⋅π
μ40
又因l d ϖ
具有任意性,故
Ω∇=π
μ40I B ϖ
(2) 再看⎰⋅L
l d B ϖ
ϖ
上述场点P 为指定点,在P 处一元位移l d ϖ
所引起结果。
现P 点沿安培环路L
移动一周,则
⎪⎩
⎪
⎨⎧=⋅=∆Ω'=⋅=∆Ω'⎰⎰L L I l d B L L b l d B L L a .4;
000μπϖ
ϖϖϖ,有:变总量相套链,则因立体角改与、若,有:变总量不套链,则因立体角改与、若 (3) 最后再用叠加原理
以上为单回路L ',若多载流回路,则从叠加原理知,每一回路均有上述结 论,进而有一般式:
⎰
∑=⋅L
L I l d B )
(0内μϖ
ϖ
5、说明
(1) 安培环路定理表达式中左边的B ϖ
是空间所有电流在回路处的合场,其积分结果可以用回路所围电流之代数和表示。
(区分:场本身与环流含义不同!)
(2) 磁场为无源有旋场,在磁场中一般不能象电场中那样引入标势描述。
(3) 两种类型举例:如图5-21,结果分别为
I l d B L
02μ-=⋅⎰ϖϖ ;
⎰
-=⋅L
I I l d B )(210μϖ
ϖ。
图5-21
三、安培环路定理应用举例
上述两定理普遍适用,但单独用⎰
∑=⋅L
l I l d B 内
0μϖ
ϖ解决问题,范围有限,只用
于问题具有某种对称性情况。
解决问题时,首先分析对称性,然后取安培环路L
过场点,再用定理求出场B ϖ。
例1:无限长载流I 的直导线外之场。
解:问题具有Z 轴对称性
∵,20I rB μπ=
∴θπμ)ϖr
I B 20=
该结果在前已有。
例2:无限长载流为I 、半径R 的圆截面载流直导线,求内、外B ϖ
分布。
解:如图5-22,电流密度2
R
I
j π=,导线内、外场点之场均呈轴对称,且方向沿圆周切向。
① R r >:I r B 02μπ=⋅
r
I
B πμ20=
∴ ② R r <:2
2
2r R
I r B ππμπ=⋅
2
02R r
I B πμ=
∴
r B ~ 曲线参见图5-22。
I
L
I
I 2
I 3
I 4
L
→
↓
例3:求螺绕环内的磁场。
设螺绕环平均半径为R ,总N 匝,载流I 。
解:经对称分析可知,B ϖ
沿圆周等大、方向沿切向,安培环路取半径R 的圆,则
NI RB 02μπ= nI R
N
I
B 002μπμ==∴内、0=外B 。
Z I R
P
B ϖ
B
O
R r
正比 反μ0I ∕2πR 图5-22。