下载文档原格式
D CBA 、B 、C 、D 、初二升初三数学测试题一、选择题(每小题有且只有一个答案正确，每小题4分，共40分) 1、如图，两直线a ∥b ，与∠1相等的角的个数为( ) A 、1个 B 、2个 C 、3个 D 、4个2、不等式组x>3x<4⎧⎨⎩的解集是( )A 、3<x<4B 、x<4C 、x>3D 、无解 3、如果a>b ，那么下列各式中正确的是( ) A 、a 3<b 3-- B 、a b<33C 、a>b --D 、2a<2b -- 4、如图所示，由∠D=∠C,∠BAD=∠ABC 推得△ABD ≌△BAC ，所用的的判定定理的简称是( ) A 、AAS B 、ASA C 、SAS D 、SSS5、已知一组数据1，7，10，8，x ，6，0，3，若x =5，则x 应等于( ) A 、6 B 、5 C 、4 D 、26、下列说法错误的是( )A 、长方体、正方体都是棱柱；B 、三棱住的侧面是三角形；C 、六棱住有六个侧面、侧面为长方形；D 、球体的三种视图均为同样大小的图形； 7、△ABC 的三边为a 、b 、c ，且2(a+b)(a-b)=c ，则( ) A 、△ABC 是锐角三角形； B 、c 边的对角是直角； C 、△ABC 是钝角三角形； D 、a 边的对角是直角；8、为筹备班级的初中毕业联欢会，班长对全班学生爱吃哪几种水果作了民意调查，那么最终买什么水果，下面的调查数据中最值得关注的是( )A 、中位数；B 、平均数；C 、众数；D 、加权平均数；9、如右图，有三个大小一样的正方体，每个正方体的六个面上都按照相同的顺序，依次标有1，2，3，4，5，6这六个数字，并且把标有“6”的面都放在左边，那么它们底面所标的3个数字之和等于( )A 、8B 、9C 、10D 、1110、为鼓励居民节约用水，北京市出台了新的居民用水收费标准：(1)若每月每户居民用水不超过4立方米，则按每立方米2米计算；(2)若每月每户居民用水超过4立方米，则超过部分按每立方米4.5米计算(不超过部分仍按每立方米2元计算)。
八升九暑假数学测试卷姓名 测试时间/ 日期________ 点评老师_________ 层次/ 时段____________ 一>填空题:1. 分解因式 =++-ay ax y x 22 .2. 若345x y z==，则x y z z ++＝ .3. 若分式1(3)(1)x x x --+ 的值为零，则x 等于 ．4.如图，直线b ax y +=经过A 、B 两点，则关于x 的不等式1-<+b ax 的解集是 ．5.如图，点1234A A A A ，，，在射线OA 上，点123B B B ，，在射线OB 上，且112233AB A B A B ∥∥，213243A B A B A B ∥∥．若212A B B △，323A B B △的面积分别为1，4，则图中三个阴影三角形面积之和为 二>选择题:1．已知0)3(2=++++m y x x 中，y 为负数，则m 的取值范围是( )A 、3>mB 、3<mC 、3->mD 、3-<m2．△ABC 的三边满足ab c bc a 2222-=-，则△ABC 是（ ）A 、等腰三角形B 、直角三角形C 、等边三角形D 、锐角三角形 3.两个连续的奇数的平方差总可以被 k 整除，则k 等于（ ）A 、4B 、8C 、4或-4D 、8的约数 4.已知k b a ca cbc b a =+=+=+，且a,b,c 为正数，则下列四个点中在函数y=kx 图象上的点的坐标为（ ）A 、（1，21）B 、（1，－21） C 、（1，2） D 、（1，－1）5.某厂接到720件衣服的定单，预计每天做48件，正好按时完成，后因客户要求提前5天交货， 设每天应多做x 件，则x 应满足的方程为（ ）．A 、54872048720=-+xB 、x -=+48720548720C 、572048720=-xD 、54872048720=+-x6.如图，已知ABCD 中，45DBC = ∠，DE BC ⊥于E ，BF CD ⊥于F ，DE BF ，相交于H ，BF AD ，的延长线相交于G ，下面结论：①.DB =;②.A BHE =∠∠;③.AB BH =; ④.BHD BDG △∽△其中正确的结论是（ ）A ．①②③④B ．①②③C ．①②④D ．②③④第4题图1 2 3 4三>解答题 1. 解方程:①.⎪⎩⎪⎨⎧+<-≤+--)1(3151215312x x x x ②. x xx x x x x --+=+--+--75178213222. 某公司需在一个月（31天）内完成新建办公楼装修工程．如果由甲、乙两队合做，12天可以完成；如果由甲、乙两队单独做，甲队单独完成所用的时间是乙队单独完成所用时间的23．（1）求甲、乙两队单独完成此工程所需的时间．（2）若请甲队施工，公司每日需付费用2000元；若请乙队施工，公司每日需付费用1400元．在规定时间内，有下列三种方案:方案一：请甲队单独施工完成此工程；方案二：请乙队单独施工完成此工程；方案三：甲、乙两队合做完成此工程．以上三种方案哪一种费用最少？3. 如图，平面直角坐标系中，四边形OABC 为矩形，点A B ，的坐标分别为(40)43()，，，，动点M N ，分别从O B ，同时出发，以每秒1个单位的速度运动．其中，点M 沿OA 向终点A 运动，点N 沿BC 向终点C 运动，过点M 作MP OA ⊥，交AC 于P ，连结NP ，已知动点运动了x 秒．（1）P 点的坐标为（ ， ）（用含x 的代数式表示）； （2）试求NPC △面积S 的表达式；（3）当x 为何值时，NPC △是一个等腰三角形？简要说明理由．。
数学一、选择题（每题4分，共40分）1. 下列数中，不是有理数的是（）A. -3.14B. √4C. 0.1010010001...D. -√92. 下列方程中，解为正数的是（）A. x - 2 = 0B. 2x + 1 = 0C. 3x - 5 = 0D. -4x + 3 = 03. 已知一元二次方程 ax^2 + bx + c = 0（a ≠ 0）的根的判别式为Δ = b^2 - 4ac，若Δ > 0，则方程有两个（）A. 相等的实数根B. 不相等的实数根C. 相等的复数根D. 不相等的复数根4. 在直角坐标系中，点A（2，3）关于x轴的对称点是（）A.（2，-3）B.（-2，3）C.（2，-3）D.（-2，-3）5. 下列函数中，是反比例函数的是（）A. y = 2x + 3B. y = x^2C. y = 3/xD. y = √x6. 在梯形ABCD中，AD ∥ BC，若AB = 5cm，BC = 12cm，AD = 6cm，则梯形的高h是（）A. 2cmB. 3cmC. 4cmD. 5cm7. 在三角形ABC中，∠A = 90°，∠B = 45°，则∠C的度数是（）A. 45°B. 90°C. 135°D. 180°8. 下列图形中，是轴对称图形的是（）A. 正方形B. 等腰三角形C. 平行四边形D. 梯形9. 已知正方形的对角线长为10cm，则该正方形的边长是（）A. 5cmB. 10cmC. 15cmD. 20cm10. 在△ABC中，若∠A = 30°，∠B = 45°，则∠C的度数是（）A. 30°B. 45°C. 60°D. 75°二、填空题（每题4分，共40分）1. 若x = 2是方程2x - 3 = 0的解，则x = _______是方程2x + 3 = 0的解。
#### 一、选择题（每题5分，共25分）1. 下列选项中，不是一元一次方程的是：A. 2x + 3 = 7B. 3x - 5 = 2x + 1C. x^2 - 4 = 0D. 4x = 122. 若a、b是方程x^2 - (a + b)x + ab = 0的两个根，则a + b的值是：A. 0B. aC. bD. a + b3. 在直角坐标系中，点A（2，3）关于y轴的对称点坐标是：A. （2，-3）B. （-2，3）C. （-2，-3）D. （2，-3）4. 若一个三角形的两边长分别为3和4，则第三边的长度可能是：A. 5B. 6C. 7D. 85. 下列函数中，是反比例函数的是：A. y = 2x + 3B. y = 3/xC. y = x^2D. y = x^3#### 二、填空题（每题5分，共25分）6. 若a = 2，b = 3，则a^2 + b^2的值是______。
7. 在直角坐标系中，点P（-3，4）到原点O的距离是______。
8. 一个等腰三角形的底边长为8，腰长为6，则这个三角形的面积是______。
9. 若一个数的3倍与它的4倍的和是48，则这个数是______。
10. 若sin A = 1/2，则角A的度数是______。
#### 三、解答题（每题10分，共30分）11. 解方程：2x - 5 = 3x + 1。
12. 已知等腰三角形ABC中，AB = AC，AD是BC的中线，求证：BD = DC。
13. 已知函数y = 2x - 3，求函数的图像与x轴的交点坐标。
#### 答案：一、选择题1. C2. D3. B4. A5. B二、填空题6. 137. 58. 249. 1210. 30°三、解答题11. 解：2x - 5 = 3x + 1移项得：2x - 3x = 1 + 5合并同类项得：-x = 6系数化为1得：x = -612. 证明：在等腰三角形ABC中，AB = AC，因为AD是BC的中线，所以BD = DC，所以三角形ABC是等腰三角形。
一、选择题（每题3分，共30分）1. 下列数中，有理数是（）A. √-1B. √2C. πD. 0.1010010001…2. 已知a > 0，b < 0，则下列不等式中正确的是（）A. a > bB. a < bC. -a > -bD. -a < -b3. 下列函数中，自变量的取值范围是全体实数的是（）A. y = √(x - 1)B. y = x² - 1C. y = log₂xD. y = √(2 - x)4. 若m² + 4 = 0，则m的值为（）A. 2B. -2C. 2 或 -2D. 无解5. 下列图形中，属于相似图形的是（）A. 等腰三角形B. 正方形C. 等边三角形D. 长方形6. 已知等腰三角形底边长为8cm，腰长为10cm，则该三角形的周长为（）A. 26cmB. 24cmC. 22cmD. 18cm7. 下列方程中，无解的是（）A. 2x + 3 = 5B. 2x - 3 = 5C. 2x + 3 = -5D. 2x - 3 = -58. 下列命题中，正确的是（）A. 若a > b，则a² > b²B. 若a > b，则a - b > 0C. 若a > b，则a + b > 0D. 若a > b，则a - b < 09. 下列函数中，单调递增的是（）A. y = 2x + 3B. y = -2x + 3C. y = 2x - 3D. y = -2x - 310. 下列数中，绝对值最小的是（）A. -1B. 0C. 1D. -3二、填空题（每题3分，共30分）11. 已知x² - 5x + 6 = 0，则x的值为______。
12. 若a² + b² = 1，则ab的最大值为______。
13. 下列函数中，自变量的取值范围是全体实数的是______。
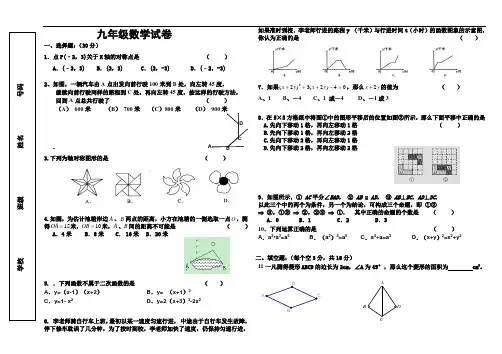
九年级数学试卷一、选择题：（30分）1．点P(–2，3)关于X 轴的对称点是 （ ） A ．(–2，3) B ．(2，3) C ．(2，-3) D ．(–2，-3)2、如图，一辆汽车由A 点出发向前行驶100米到B 处，向左转45度，继续向前行驶同样的路程到C 处，再向左转45度，按这样的行驶方法， 回到A 点总共行驶了 （ ） （A ） 600米 （B ） 700米 （C ）800米 （D ） 900米． 3.下列为轴对称图形的是（）4.如图，为估计池塘岸边A 、B 两点的距离，小方在池塘的一侧选取一点O ，测得15=OA 米，10=OB 米，A 、B 间的距离不可能是 （ ） A ．4米 B．8米 C ． 16米 D ．20米5. ．下列函数不属于二次函数的是 （ ）A ．y=（x-1）（x+2）B ．y= （x+1）2C ．y=1- x 2D ．y=2（x+3）2-2x 26. 李老师骑自行车上班，最初以某一速度匀速行进，•中途由于自行车发生故障，停下修车耽误了几分钟，为了按时到校，李老师加快了速度，仍保持匀速行进，如果准时到校．李老师行进的路程y•（千米）与行进时间t （小时）的函数图象的示意图，你认为正确的是 （ ）7．如果04)2(3)2(2=-+++y x y x ，那么y x 2+的值为 （ ） A 、1 B 、－4 C 、1 或－4 D 、－1或38．在5×5方格纸中将图①中的图形平移后的位置如图②所示，那么下面平移中正确的是 A.先向下移动1格，再向左移动1格 （ ） B.先向下移动1格，再向左移动2格 C.先向下移动2格，再向左移动1格 D.先向下移动2格，再向左移动2格 9．如图所示，① AC 平分∠BAD ， ② AB = AD ， ③ AB ⊥BC ，AD ⊥DC. 以此三个中的两个为条件，另一个为结论，可构成三个命题，即 ①②⇒ ③，①③ ⇒ ②，②③ ⇒ ①． 其中正确的命题的个数是 （ ） A ．0 B ．1 C ．2 D ．3 10．下列运算正确的是 （ ） A ．a 2•a 3=a 6 B ．（a 2）4=a 6 C ．a 4÷a=a 3 D ．（x+y ）2=x 2+y 2二、填空题：（每个空3分，共18分） 11一凡测得菱形ABCD 的边长为2cm ，∠A 为45°，那么这个菱形的面积为 cm 2。
一、选择题（每题5分，共50分）1. 下列数中，既是质数又是合数的是（）A. 4B. 9C. 15D. 172. 如果a > b，那么下列不等式中错误的是（）A. a + 3 > b + 3B. 2a > 2bC. a - 5 > b - 5D. a / 2 > b / 23. 已知等腰三角形底边长为6，腰长为8，则该三角形的周长为（）A. 22B. 24C. 26D. 284. 在直角坐标系中，点A（2，3）关于x轴的对称点坐标是（）A.（2，-3）B.（-2，3）C.（-2，-3）D.（2，-3）5. 一个长方形的长是8厘米，宽是5厘米，它的面积是（）A. 40平方厘米B. 32平方厘米C. 45平方厘米D. 48平方厘米6. 下列函数中，在定义域内是单调递增的是（）A. y = -x^2 + 4B. y = 2x - 3C. y = x^2 - 2x + 1D. y = -3x + 27. 已知一元二次方程x^2 - 5x + 6 = 0，下列选项中，不是方程的根的是（）A. 2B. 3C. 6D. -18. 下列图形中，不是平行四边形的是（）A. 矩形B. 菱形C. 正方形D. 梯形9. 已知圆的半径为5厘米，其周长为（）A. 15π厘米B. 25π厘米C. 10π厘米D. 20π厘米10. 下列分数中，值最大的是（）A. 1/2B. 3/4C. 2/3D. 4/5二、填空题（每题5分，共50分）11. 一个数加上它的3倍等于27，这个数是______。
12. 如果一个三角形的两个内角分别是45°和60°，那么第三个内角的度数是______。
13. 下列等式中，正确的是______。
14. 已知函数y = 2x - 1，当x = 3时，y的值为______。
15. 下列方程中，解为整数的是______。
16. 下列图形中，面积最大的是______。
一、选择题（每题3分，共30分）1. 下列各数中，正整数是（）A. -2B. 0.5C. -√4D. 32. 若方程2x - 5 = 3的解为x，则x的值为（）A. 2B. 3C. 4D. 53. 在下列函数中，一次函数是（）A. y = x^2 + 1B. y = 2x - 3C. y = √xD. y = 3/x4. 下列图形中，是平行四边形的是（）A. 矩形B. 等腰梯形C. 等边三角形D. 等腰三角形5. 若a > b，则下列不等式中正确的是（）A. a + 2 > b + 2B. a - 2 < b - 2C. a + 2 < b + 2D. a - 2 > b - 26. 已知等腰三角形的底边长为6cm，腰长为8cm，则该三角形的面积为（）A. 24cm²B. 28cm²C. 32cm²D. 36cm²7. 若x² - 5x + 6 = 0，则x的值为（）A. 2B. 3C. 4D. 58. 下列各式中，绝对值最大的是（）A. |2|B. |-3|C. |-1|D. |0|9. 在直角坐标系中，点P（2，3）关于x轴的对称点为（）A. （2，-3）B. （-2，3）C. （2，-3）D. （-2，-3）10. 下列各式中，同类项是（）A. 2x²和3x³B. 4xy和5xyC. 3x和5x²D. 6y²和-6y²二、填空题（每题3分，共30分）11. 若a² - 4 = 0，则a的值为________。
12. 在△ABC中，若∠A = 60°，∠B = 45°，则∠C的度数为________。
13. 若a = 3，b = -2，则a² + b²的值为________。
14. 下列函数中，y = kx + b是一次函数，则k和b的取值范围分别是________和________。
数学八升九测试卷(方用)班级：________姓名：_________分数：_________一、选择题(每小题3分,共302.矩形具有而菱形不具有的性质是()A.两组对边分别平行B.对角线相等C.对角线互相平分) ×=4 B.+= C.÷=2 D.=-154.(2013·陕西中考y()A.1B.-1C.3D.-35.(2013·盐城中考)某公司10,3 4.24交于点O,下列条件不能判定这个四边形是平行四边形的是()A.AB∥DC,AD∥BC的A.24B.16C.4D.28.如图,△ABC和△DCE都是边长为4的等边三角形,点B,C,EB.2正比例函数y=kx(k,是()10.(2013·黔西南州中考)如图,B.x<3C.x>D.x>3分,共24分)11.计算:-=.12.(2013·恩施州中考)函数y=的自变量x的取值范围表,则这10人成绩的平均数为.形ABCD 中,点E,F 分别在边BC,AD 上,请添加一个条件,使四边形AECF是平行四边形(只填一个即可).8O,AC18.(2013·上海中考)李老师开车从甲地到相距240km的乙地,如果油箱剩余油量y(L)与行驶里程x(km)之间是一次函数地时油箱剩余油量(2)(2-1)(+1)-(1-2)2.化:÷·21.(6分)(2013·武汉中考)直线y=2x+b经过点(3,5),求关于x的不等式2x+b≥0的解集.圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.(1)请你判断所画四边形的形状,并说明理由.如DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.A不符合题意;矩形的对角线相等,菱形的对角线不一定相等,故选项B正确;矩形与菱形的对角线都互相平分,故选项C.×=,与不能合并,÷===2,==15,因此只有选项C4.【解析】选A.一次函数的解析式为y=kx+b(k≠0),∵x=-2时y=3;x=1时y=0,∴解得2400,到大的顺序排列,位于第5个的是2400,第6个的也是2400,故中位数是=2400.6.【解析】选D.由“AB∥DC,AD由“AO=CO,BO=DO”可知,四边形ABCD的两条对角线互相平分,则该四边形是平行四边形.故选项C不符合题意;由“AB∥AC⊥BD,OA=AC=3,OB=BD=2,AB=BC=CD=AD,∴在Rt△AOB=,AB=4.BDE=90°.∴BD==4.9.【解析】选A.∵正比例函数y=kx(k≠0)的函数值y随x的A(m,3),的解集为x<.11.【解析】-=3-=.答案:12.【解析】3-x≥0且x+2≠0,∵+|a-b|=0,=0,且a-b=0,c14.【解析】×(5×3+4×1+3×2+2×2+1×2)=×(15+4+6+4+2)=×31=3.1.所以这10人成绩的平均数为AF=CE,理由是:∵四边形ABCD 是平行四边形,∴AD∥BC,∴AF∥CE,∵AF=CE,∴四边形AECF是平行四边形.是8∵AO∶BO=1∶2,∴AO=2,BO=4,∴菱形ABCD的面积S=×2×4×4=16.得解得y=-x+3.5.x=240,y=-×19.【解析】(1)9+7-5+2=9+14-20+==.(2)(2-1)(+1)-(1-2)2-1-(1-4+12)--1-1+4-12=(2-1+4)-8=5-8.【解析】÷·=··=a=-2==.【解析】∵直线经过点(3,5),∴5=2×3+b,解得b=-1,∵2x+b≥0,∴2x-1≥0,解得x≥.∠EF=AE=8cm.23.【解析】(1)∵四边形ABCD∴四边形AMDN是平行四边形.(2)AM=1.理由如下:∵四边形ABCD是菱形,∴AD=AB=2,,,AM=AD=1.24.∠BDE=90°,∴AF=2CF=2xm,在Rt△ACF中,根据勾股定理得∴x===7070-70(m).70(1.73-1)=70×0.73=51.1(m)<3×20(m),∴我支持小华的观点,这楼不到20层.25.【解析】(1)∵CD∥x轴,A(0,6),B(30,12),∴解得所以,直线AC的解析式为y=x+6(0≤x≤50),x+6(0则平均数为=7(环),中位数为7.5环,方差为[(2-7)2+(4-7)2+(6-7)2+(8-7)2+(7-7)2+(7-7) 2222环),成绩为2,6,6,7,7,7,8,9,9,9,中位数为7(环),方差为[(2-7)2+(6-7)2+(6-7)2+(7-7222)2(2)由甲的方差小于乙的方差,得到甲胜出.(3)希望乙胜出,规则为9环与10环的总环数大的胜出,因为甲。
一、选择题（每题5分，共50分）1. 下列各数中，正数是（）A. -3B. 0C. -2D. 52. 若a=3，b=-4，则a²+b²的值为（）A. 9B. 16C. 7D. 53. 在直角坐标系中，点P（2，3）关于y轴的对称点为（）A. （-2，3）B. （2，-3）C. （-2，-3）D. （2，3）4. 若x=2，则2x+3的值为（）A. 7B. 5C. 4D. 35. 若一个等腰三角形的底边长为6cm，腰长为8cm，则这个三角形的面积为（）A. 24cm²B. 32cm²C. 36cm²D. 48cm²6. 下列各式中，正确的是（）A. a²+b²=c²B. a²+b²=cC. a²+b²=c²-2abD. a²+b²=c²+2ab7. 若x+y=5，xy=6，则x²+y²的值为（）A. 19B. 21C. 25D. 298. 下列函数中，是反比例函数的是（）A. y=x²B. y=2xC. y=2/xD. y=3x+49. 在等差数列中，若第一项为2，公差为3，则第10项的值为（）A. 28B. 30C. 32D. 3410. 若一个圆的半径为5cm，则其周长的值为（）A. 15πcmB. 20πcmC. 25πcmD. 30πcm二、填空题（每题5分，共50分）11. 若x²+4x+4=0，则x的值为______。
12. 在直角坐标系中，点A（2，3）关于x轴的对称点为______。
13. 若一个等腰三角形的底边长为8cm，腰长为10cm，则这个三角形的面积为______cm²。
14. 若x=3，则2x²-3x+2的值为______。
15. 在等差数列中，若第一项为-3，公差为2，则第5项的值为______。
乐平五中2017年八升九数学试卷（满分150分 考试时间120分钟）一、选择题（本大题共10小题，每小题只有一个选项正确，每 小题4分，共40分）1、如图所示,在长方形ABCD 的对称轴l 上找点P,使得△PAB,△PBC,△PDC,△PAD 均为等腰三角形,则满足条件的点P 有.(?????? )A 、5个B 、4个C 、3个D 、1个第1题图 第6题图 2．已知 化简二次根式的正确结果为（ ）A. yB. y -C. y -D. y --3．已知梯形ABCD 的四个顶点的坐标分别为A （－1，0），B （5，0），C （2，2），D （0，2），直线y=kx +2将梯形分成面积相等的两部分，则k 的值为（ ）A. －32B. －92C. －74D. －724、某校进行校园歌手大奖赛预赛,评委给每位选手打分时,最高分不超过10分,所有评委的评分中去掉一个最高分,去掉一个最低分后的平均分即为选手的最后得分.小敏的最后得分为分,若只去掉一个最低分,小敏的得分为分,若只去掉一个最高分,小敏的得分为分,那么可以算出这次比赛的评委有(?????? ) A 、9名 B 、10名 C 、11名 D 、12名 5．若x 取整数，则使分式的值为整数的x 值有（ ） A ．3个 B ．4个 C ．6个 D ．8个6．如图，在四边形ABCD 中，对角线AC 平分∠BAD ，AB ＞AD ，下列结论中正确的是（ ）A ．AB ﹣AD ＞CB ﹣CD B ．AB ﹣AD=CB ﹣CDC ．AB ﹣AD ＜CB ﹣CD D ．AB ﹣AD 与CB ﹣CD 的大小关系不确定 7．边长分别是3、5、8的三个正方体被粘合在一起，在这些用各种方式粘合在一起的立体中，表面积最小的那个立体的表面积是（ ） A ．570 B ．502 C ．530 D ．538 8、小敏尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A 点的直线折叠,使得B 点落在AD 边上的点F 处,折痕为AE(如图②); 再沿过D 点的直线折叠, 使得 C 点落在DA 边上的点N 处, E 点落在AE 边上的点M 处,折痕为 DG(如图).如果第二次折叠后,M 点正好在∠NDG 的平分线上,那么矩形ABCD 的长与宽的比值第8题图 第9题图 第A 、2B 、3C 、D 、9.如图，P 为ABC ∆内一点，070,BAC ∠=BP∠是ABP ∠的平分线，CE 是ACP ∠的平分线，BD则BFC ∠=.A 085 .B 090 .C 095 .D 10.如图，一次函数221+-=x y 的图像上有两点A坐标为2，B 点的横坐标为40(<<a a 且)2≠a 别作x 轴的垂线，垂足分别为C ，D ，△AOC ，△B 分别为S 1，S 2，则S 1，S 2的大小关系是＞S 2 =S 2 C. S 1＜S 2 D.无法确定二、填空题（本大题共6小题，每小题5分，共3011、如图,边长为1的正方形ABCD 绕点A 逆时针旋转正方形AB′C′D′,则围成图中阴影部分的周长和面________12已知a=3+22，b=3-22，则a 2b-ab 2=_13.如图，已知四边形ABCD 的对角互补，且,15BAC DAC AB ∠=∠=,12.AD = 过顶点C,E 则AEBE= . 第13题图 第 第11题图14．如图，已知五边形ABCDE 中，∠ABC=∠AB=CD=AE=BC+DE=2，则五边形ABCDE 的面积15．设a 为常数，多项式x 3+ax 2+1除以x 2﹣为x+3，则a= ．16多项式x 2+y 2﹣6x+8y+7的最小值为 ．三、（本大题共4小题，每小题6分，共24分）0xy f（3）若以点,,,M O P Q 为顶点的四边形是矩形，请直接写出相应的m 的值．26．（ 14分）如图（1），在正方形ABCD 中，E 是AB 上一点，F 是AD 延长线上一点，且DF=BE ．容易证得：CE=CF ； （1）在图1中，若G 在AD 上，且∠GCE=45°．试猜想GE 、BE 、GD 三线段之间的数量关系，并证明你的结论．（2）运用（1）中解答所积累的经验和知识，完成下面两题：①如图（2），在四边形ABCD 中∠B=∠D=90°，BC=CD ，点E ，点试探索当α和β满足什么关系时，图（1）中GE 、BE 、GD 三线段之间的关系仍然成立，并说明理由．②在平面直角坐标中，边长为1的正方形OABC 的两顶点A 、C 分别在y 轴、x 轴的正半轴上，点O 在原点．现将正方形OABC 绕O 点顺时针旋转，当A 点第一次落在直线y=x 上时停止旋转，旋转过程中，AB 边交直线y=x 于点M ，BC 边交x 轴于点N （如图（3））．设△MBN 的周长为p ，在旋转正方形OABC 的过程中，p 值是否有变化？请证明你的结论． 乐平五中2017年八升九数学试卷答案 1、【答案】C【考点】等腰三角形的判定与性质 【解析】【解答】如图，当以AB 为底边时，只在P 1符合； 当以AB 为腰时，以AB 为半径，分别以A ，B 为圆心作圆，与直线l 分别交于点P 2 ， P 3 ， 此时P 2 ， P 3符合 4、【答案】A【考点】一元一次方程的应用 【解析】【解答】解：设这次比赛的评委有x 人， 去掉最高分和最低分后的总得分是﹙x-2﹚×， 去掉最低分后的总得分是﹙x-1﹚×， 去掉最高分后的总得分是﹙x-1﹚×， 那么最高分为﹙x-1﹚×﹙x-2﹚×=+， 最低分为﹙x-1﹚×﹙x-2﹚×=， 根据题意得：＜最高分≤10，最低分＜， ＜+≤10，， ∴2＜x≤9，x ＞2． ∴这次比赛的评委有9名． 故选：A ．5【考点】分式的值；整式的除法．【分析】首先把分式转化为3+，则原式的值是整数，即可转化为讨论的整数值有几个的问题．考点】全等三角形的判定与性质；三角形三边关系．6【分析】在AB 上截取AE=AD ，则易得△AEC ≌△ADC ，则则AB ﹣AD=BE ，放在△BCE 中，根据三边之间的关系【解答】解：如图，在AB 上截取AE=AD ，连接CE ．∵AC 平分∠BAD ， ∴∠BAC=∠DAC ， 又AC 是公共边，∴△AEC ≌△ADC （SAS ）， ∴AE=AD ，CE=CD ，∴AB ﹣AD=AB ﹣AE=BE ，BC ﹣CD=BC ﹣CE ， BCE 中，BE ＞BC ﹣CE ， ∴AB ﹣AD ＞CB ﹣CD ． 故选A ．7【考点】几何体的表面积．【分析】先求出边长分别是3、5、8的三个正方体的再减去边长是3的两个正方形的面积和的4倍、边长方形的面积和的2倍，即为所求． 【解答】解：（3×3+5×5+8×8）×6﹣（3×3）×=98×6﹣9×4﹣25×2 =588﹣36﹣50 =502． 故选B ．8、【答案】C 【考点】翻折变换（折叠问题）【解析】【解答】解：连接DE ，如图，∵沿过A 点的直线折叠，使得B 点落在AD 边上的点∴四边形ABEF 为正方形， ∴∠EAD=45°，由第二次折叠知，M 点正好在∠NDG 的平分线上， ∴DE 平分∠GDC ， ∴Rt △DGE ≌Rt △DCE ， ∴DC=DG ，又∵△AGD 为等腰直角三角形， ∴AD=DG=CD ，∴矩形ABCD 长与宽的比值= ．10 AQ P ME D CBAO yx（第25题）故答案为：4．15【解答】解：∵多项式x3+ax2+1除以x2﹣1所得的余式为x+3，∴可设x3+ax2+1﹣（x+3）=（x2﹣1）（x+b），X取1时，得a=217【解答】解：若∠BOC在△ABC内，如下图：∵BD、CE是△ABC的高，∴∠BOC=360°﹣∠A﹣∠ADO﹣∠AEO=120°；若∠BOC在△ABC外，如下图：∵BD、CE是△ABC的高，∴∠BOC=90°﹣∠DCO=90°﹣∠ACE=∠A=60°．故答案为：120°或60°．18 BC的解析式是y=x+4．19．已知a=2015x+2014，b=2015x+2015，c=2015x+2016．求a2+b2+c2－ab－bc－ca的值=320证明：延长AB到F,使=BD,连DF,所以∠F=∠BDF因为∠=80 所以∠F=40°因为∠ACB=40度所以∠F=∠ACB,因为AD是平分线所以∠BAD=∠又AD为公共边所以△≌△所以AF=AC因为AD是，所以∠=∠/2=40所以∠=∠C所以BE=EC,所以BE+AE=EC+AE=AC=AF=AB+=AB+BD。
22【解答】证明：（1）∵四边形ABCD是正方形，∴AD=CD，∠ADC=90°，∴∠A′DE=90°，根据旋转的方法可得：∠EA′D=45°，∴∠A′ED=45°，∴A′D=ED，在△AA′D和△CED 中，∴△ADA′≌△CDE（SAS）；（2）由正方形的性质及旋转，得CD=CB′，∠CB′E=∠CDE=90°，又CE=CE，∴Rt△CEB′≌Rt△CED∴∠B′CE=∠DCE，∵AC=A′C∴直线CE是线段AA′的垂直平分线．23解法一：过P 作PE ∥QC????????????????????则△AFP是等边三角形，∵P 、Q 同时出发、速度相同，即BQ=AP∴BQ=PF∴△DBQ≌△DFP,∴BD=DF∵,∴BD=DF=FA=,∴AP=2.解法二：??∵P 、Q 同时同速出发，∴AQ=BQ设AP= PC=6-x，QC=6+x在Rt△QCP中，∠CQP=30°,∠C=60°∴∠CQP=90°∴QC=2PC,即6+x=2（6-x）∴x=2∴AP=2（2）由（1 ）知BD=DF而△APF 是等边三角形，PE ∵AE=EF 又DE+(BD+AE)=AB=6,?∴DE+(DF+EF)=6 ，?即DE+DE=6?∵DE=3 为定值，即DE 的长不变24解：设x a、x b、x c分别表示答对题a、题b、题则有，由①+②+③得x a+x b+x c=37 ④由④﹣①得x c=8同理可得x a=17，x b=12∴答对一题的人数为37﹣1×3﹣2×15=4，全班人1+4+15=20。
