第五章运筹学 线性规划在管理中的应用案例

第五章线性规划在管理中的应用某企业停止了生产一些已经不再获利的产品，这样就产生了一部分剩余生产力。

管理层考虑将这些剩余生产力用于新产品Ⅰ、Ⅱ、Ⅲ的生产。

可用的机器设备是限制新产品产量的主要因素，具体数据如下表：司的利润最大化。

1、判别问题的线性规划数学模型类型。

2、描述该问题要作出决策的目标、决策的限制条件以及决策的总绩效测度。

3、建立该问题的线性规划数学模型。

4、用线性规划求解模型进行求解。

5、对求得的结果进行灵敏度分析（分别对最优解、最优值、相差值、松驰/剩余量、对偶价格、目标函数变量系数和常数项的变化范围进行详细分析）。

6、若销售部门表示，新产品Ⅰ、Ⅱ生产多少就能销售多少，而产品Ⅲ最少销售18件，请重新完成本题的1-5。

解：1、本问题是资源分配型的线性规划数学模型。

2、该问题的决策目标是公司总的利润最大化，总利润为：+ +决策的限制条件：8x1+ 4x2+ 6x3≤500 铣床限制条件4x1+ 3x2≤350 车床限制条件3x1+ x3≤150 磨床限制条件即总绩效测试（目标函数）为：max z= + +3、本问题的线性规划数学模型max z= + +S．T．8x1+ 4x2+ 6x3≤5004x1+ 3x2≤3503x1+ x3≤150x1≥0、x2≥0、x3≥04、用Excel线性规划求解模板求解结果：最优解（50，25，0），最优值：30元。

5、灵敏度分析目标函数最优值为: 30变量最优解相差值x1 50 0x2 25 0x3 0 .083约束松弛/剩余变量对偶价格1 0 .052 75 03 0 .033目标函数系数范围:变量下限当前值上限x1 .4 .5 无上限x2 .1 .2 .25x3 无下限.25 .333常数项数范围:约束下限当前值上限1 400 500 6002 275 350 无上限3 150（1）最优生产方案：新产品Ⅰ生产50件、新产品Ⅱ生产25件、新产品Ⅲ不安排。

简单的运筹学实际应用案例运筹学（Operations Research）是一门研究如何有效利用有限资源进行决策的学科，它通过数学、统计学和经济学等方法，帮助管理者做出最佳决策。

下面将介绍几个简单的运筹学实际应用案例。

1.生产线优化假设一公司拥有多条生产线，每条生产线对应不同的产品。

公司希望通过优化生产线的调度，以达到最大的产出和利润。

运筹学可以通过数学模型和算法，对生产线进行优化调度。

例如，可以使用线性规划模型来确定每条生产线的产量和调度，以最大化总利润；也可以使用整数规划模型来考虑生产线的限制和约束条件。

2.物流网络设计一家物流公司需要设计其物流网络，以最小化成本并满足客户对快速物流的需求。

运筹学可以通过数学模型和算法，帮助物流公司优化物流网络的设计。

例如，可以使用网络流模型来确定货物在物流网络中的最佳路线和节点，以最小化总运输成本；也可以使用线性规划模型来决定在不同节点上的仓库和货物库存量，以满足客户的需求。

3.航班调度问题一家航空公司需要制定最佳航班调度计划，以最大化航班利润并排除延误风险。

运筹学可以通过数学模型和算法，帮助航空公司优化航班调度。

例如，可以使用线性规划模型来决定不同航班的起降时间和机型，以最大化航班利润；也可以使用排队论模型来评估航班的延误风险，并制定相应的调度策略。

4.人员调度问题一家超市需要制定最佳的员工调度计划，以最大化服务质量和节约人力成本。

运筹学可以通过数学模型和算法，帮助超市优化员工调度。

例如，可以使用整数规划模型来决定不同时间段需要多少员工，并考虑员工的技能匹配和工作时间的合理安排；也可以使用模拟仿真方法来评估不同调度策略的效果，并做出相应的决策。

以上是几个简单的运筹学实际应用案例，运筹学在实际生产和管理中有着广泛的应用。

通过数学模型和算法的应用，可以帮助企业优化资源配置、提高效率和决策质量，从而实现最佳的经济效益。

线性规划应用案例分析线性规划是一种在数学和运营管理中常见的优化技术。

它涉及到在一组线性不等式约束下，最大化或最小化一个线性目标函数。

这种技术可以应用于许多不同的领域，包括供应链管理、资源分配、投资组合优化等。

本文将探讨几个线性规划应用案例，以展示其在实际问题中的应用和价值。

某制造公司需要计划生产三种产品，每种产品都需要不同的原材料和生产时间。

公司的目标是最大化利润，但同时也受到原材料限制、生产能力限制以及每种产品市场需求限制的约束。

通过使用线性规划，该公司能够找到最优的生产计划，即在满足所有约束条件下，最大化利润。

某物流公司需要计划将货物从多个产地运输到多个目的地。

公司的目标是最小化运输成本，但同时也受到运输能力、货物量和目的地需求的约束。

通过使用线性规划，该公司能够找到最优的运输方案，即在满足所有约束条件下，最小化运输成本。

某投资公司需要将其资金分配给多个不同的投资项目。

每个项目都有不同的预期回报率和风险水平。

公司的目标是最大化回报率，同时也要保证投资风险在可接受的范围内。

通过使用线性规划，该公司能够找到最优的投资组合，即在满足所有约束条件下，最大化回报率。

这些案例展示了线性规划在实践中的应用。

然而，线性规划的应用远不止这些，它还可以用于诸如资源分配、时间表制定、路线规划等问题。

线性规划是一种强大的工具，可以帮助决策者解决复杂的问题并找到最优解决方案。

线性规划是一种广泛应用的数学优化技术，适用于在多种资源限制下寻求最优解。

这种技术涉及到各种领域，包括工业、商业、运输、农业、金融等，目的是在给定条件下最大化或最小化线性目标函数。

下面我们将详细讨论线性规划的应用。

线性规划是一种求解最优化问题的数学方法。

它的基本思想是在一定的约束条件下，通过线性方程组的求解，求得目标函数的最优解。

这里的约束条件通常表现为一组线性不等式或等式，而目标函数则通常表示为变量的线性函数。

工业生产：在工业生产中，线性规划可以用于生产计划、物料调配、人力资源分配等方面。

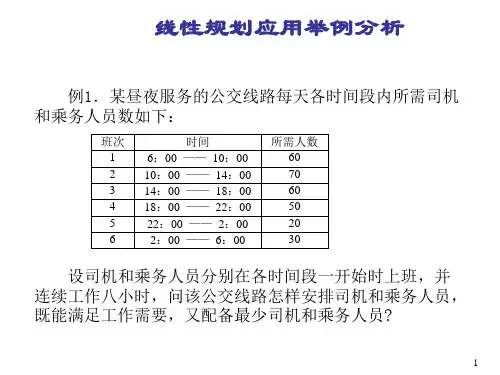
线性规划在工商管理中的应用一、人力资源分配的问题例1某昼夜服务的公交线路每天各时间段内所需司机和乘务人员人数如下表所示：设司机和乘务人员分别在各时间段开始时上班；并连续工作8小时，问该公交线路应怎样安排司机和乘务人员，既能满足工作需要，又使配备司机和乘务人员的人数最少？例2 一家中型的百货商场对售货员的需求经过统计分析如下表所示：为了保证售货员充分休息，要求售货员每周工作五天，休息两天，并要求休息的两天是连续的，问应该如何安排售货员的休息日期，既能满足工作需要，又使配备的售货员的人数最少？二、生产计划问题例3 某公司面临一个是外包协作还是自行生产的问题。

该公司有甲、乙、丙三种产品，这三种产品都要经过铸造、机械加工和装配三道工序。

甲、乙两种产品的铸件可以外包协作，亦可以自行生产，但产品丙必须由本厂铸造才能保证质量。

有关情况如下表所示，公司中可利用的总工时为：铸造8000小时，机械加工12000小时和装配10000小时。

为了获得最大利润，甲、乙、丙三种产品各应生产多少件？甲、乙两种产品的铸件有多少由本公司铸造？有多少为外包协作？三、套裁下料问题例4 某工厂要做100套钢架，每套钢架需要长度分别为2.9米、2.1米、和1.5米的圆钢各一根。

已知原料每根长7.4米，问应如何下料，可使所用原料最省？四、配料问题例5某工厂要用三种原料1、2、3混合调配出三种不同规格的产品甲、乙、丙，产品的规格要求、产品的单价、每天能供应的原材料数量及原材料单价如下表所示：问该厂应如何安排生产，才能使利润最大？五、投资问题例6某部门现有资金200万元，今后五年内考虑给以下的项目投资：项目A：从第一年到第五年每年年初都可以投资，当年末能收回本利110%；项目B：从第一年到第四年每年年初都可以投资，次年末能收回本利125%，但规定每年最大投资额不能超过30万元；项目C：第三年初需要投资，到第五年末能收回本利140%，但规定每年最大投资额不能超过80万元；项目D：第二年初需要投资，到第五年末能收回本利155%，但规定每年最大投资额不能超过100万元。

运筹学应用案例运筹学是一门应用数学，研究如何在资源有限的情况下，最优地组织和管理这些资源。

运筹学的应用范围非常广泛，涉及到各个领域。

以下是一个关于运筹学应用的实际案例。

某公司是一家制造业企业，主要生产产品A和产品B。

这家公司有两个生产车间和一个物流中心，每个车间配备了不同的生产设备。

公司的目标是最大化利润。

产品A在车间1中生产，车间1的生产设备可以在一小时内生产5个单位的产品A。

产品B在车间2中生产，车间2的生产设备可以在一小时内生产4个单位的产品B。

物流中心负责将产品A和产品B运送到市场，物流中心的运输能力为每小时20个单位。

同时，公司还面临一个资源的限制，即每天生产的产品A和产品B的总数不能超过400个单位。

另外，公司还有一个库存的限制，即每天生产的产品A和产品B的总数不能超过600个单位。

为了系统地解决这个问题，公司决定使用运筹学的方法进行决策。

首先，公司需要确定目标函数。

由于公司的目标是最大化利润，所以可以将目标函数定义为利润函数。

假设公司每个单位的产品A的利润为10美元，每个单位的产品B的利润为8美元。

那么公司的目标函数可以定义为：Z=10A+8B。

然后，公司需要确定约束条件。

根据资源的限制，可以得到以下约束条件：A≤5×小时数（车间1的生产能力）B≤4×小时数（车间2的生产能力）A+B≤400（每天生产的总数限制）A+B≤600（库存的限制）20A+20B≤600（物流中心的运输能力）接下来，公司需要确定变量的取值范围。

由于产量和库存数量为实数，所以可以将A和B的取值范围定义为非负实数。

最后，公司需要使用线性规划算法来求解最优解。

线性规划算法可以通过求解目标函数的最大值来找到最优解。

在这个案例中，可以使用单纯形法来求解最优解。

通过使用运筹学的方法，公司可以得到最优的生产和运输计划，以最大化利润。

对于公司而言，这个案例展示了如何在资源有限的情况下，通过合理的规划和管理，实现最优的生产和销售策略。

线性规划在管理中的应用摘要：本文从线性规划的概念、构成要素出发，给出了线性规划模型。

并给出了用单纯型法来求解线性规划模型的求解原理。

然后通过几个具体例子，如合理下料问题、运输问题、投资问题，建立了数学规划模型，并给出了如何对生活中有限资进行合理分配，对选择方案进行最优决策。

线性规划模型决策应用线性规划是运筹学中一种最常用的方法，线性规划在现代管理中起到了重要的作用，线性规划所处理的问题是怎样以最佳的方式在各项经济活动中分配有限的资，以便最充分地发挥资的效能去获取最佳经济效益。

线性规划在财务贸易、金融、工业制造、农业生产、交通运输、人事管理、设备维修等领域的管理决策分析^p 中均可帮助人们解决实际问题。

例如在原料分配问题上，研究如何确定各原料比例，才能降低生产成本，增加利润；在农作物规划中，如何安排各种农作物的布局，使生产率迅速提高；在生产计划安排中，选择什么样的生产方案才能提高生产产值。

线性规划为求解这类问题提供了实用性强的理论基础和具体求解方法。

一、线性规划数学模型经营管理中研究如何有效地利用现有的人力物力完成更多的任务，或在预定的任务目标下，如何耗用最少的人力物力去实现，这个统筹规划的问题用可用数学语言表达。

线性规划模型从数学角度来归纳为三点：（1）每个问题都有一组变量，称为决策变量，一般记为，一般要求。

它是决策者对决策问题需要加以考虑和控制的因素。

（2）每个问题都有决策变量需要满足一定的条件，问题的限制条件用不等式或等式来表达，它是实现企业决策目标，限制性因素对实现目标起约束作用，称为约束条件。

（3）问题的目标通过变量的函数形式来表达，称为目标函数，且目标值与决策变量之间的关系是线性关系，要求在约束条件下，求目标函数的最大值或最小值。

（4）一般的线性规划数学模型为：线性规划标准形式特点：（1）目标函数求最大值（有时求最小值）（2）约束条件都为等式方程，且右端常数项bi都大于或等于零（3）决策变量xj为非负。

运筹学在物流管理中的应用案例物流管理是现代企业运作过程中至关重要的一环，它涉及到物流规划、采购、生产、仓储、配送等各个环节。

为了提高物流运营效率并降低成本，许多企业开始运用运筹学方法来优化物流管理。

本文将通过一个实际案例，介绍运筹学在物流管理中的应用。

案例背景某电子产品制造企业为了更好地满足全球市场的需求，决定进行物流网络优化。

该企业有多个工厂分布在不同地区，需要将产品从工厂运送到全球各地的分销中心。

为了确保产品能够及时到达，以及最大程度地减少物流成本，他们决定运用运筹学工具进行物流网络优化。

方案设计在设计物流网络优化方案之前，首先要明确一些关键的因素和约束条件，例如：工厂和分销中心的地理位置、产品的生产周期和需求量、运输的成本和时效、仓储设施的容量等。

基于这些信息，可以利用运筹学方法设计以下方案：1. 物流路径规划通过运筹学模型来确定产品从工厂到分销中心的最佳路径。

在此过程中，需要考虑运输成本、距离、交通状况等因素，以及协调不同地区的供应链环节。

运筹学模型可以通过线性规划、整数规划等方法来求解，以确定最佳物流路径。

2. 运输调度优化在确定了最佳物流路径后，下一步是对运输调度进行优化。

通过运筹学方法，可以建立模型考虑不同运输方式（如海运、铁路、公路）的成本和时效，以及不同的配送方式和批量配置。

运筹学模型可以通过动态规划、启发式算法等方法来求解，以达到优化运输调度的目的。

3. 仓储设施布局在物流管理中，仓储设施的布局对于物流效率和成本控制起着重要作用。

通过运筹学方法，可以分析和优化仓储设施的布局，以减少物流路径、降低仓储和运输成本，并提高物流处理效率。

运筹学模型可以通过网络流问题、图论等方法来求解，以确定最佳仓储设施布局方案。

4. 库存管理优化库存管理是物流管理中的一个关键环节。

通过运筹学方法，可以建立库存管理模型，以决定最佳的库存水平、采购和补充策略，以及最优的订货周期。

通过运筹学模型的求解，可以降低库存成本、减少过剩库存和缺货现象，提高物流管理的响应速度和效率。

运筹学分析方法及应用案例运筹学是一门研究如何通过使用数学、统计学和计算机科学等工具来解决决策问题的学科。

其应用领域广泛，包括生产、物流、供应链管理、交通网络优化、人员调度等。

运筹学分析方法可以通过建立数学模型，优化决策方案，并通过模拟和数据分析来评估方案的效果。

下面将介绍运筹学分析方法及其应用案例。

一种常见的运筹学分析方法是线性规划。

线性规划可以用于在给定约束条件下优化目标函数的值。

一个典型的应用是生产计划问题。

假设一个公司有多个产品和多个生产资源，线性规划可以帮助确定如何安排生产以最大化利润或最小化成本。

举个例子，一个公司生产产品A和产品B，有两个生产线和一定数量的原材料。

每生产一个单位的A需要2个单位的原材料和2个单位的生产时间，每生产一个单位的B需要1个单位的原材料和4个单位的生产时间。

每个生产线每天的工作时间为8个小时，而每天的原材料供应量为10个单位。

公司希望确定每个产品在每个生产线上的产量以最大化总利润。

我们可以建立一个线性规划模型来解决这个问题。

假设x1和x2分别代表在两个生产线上生产产品A的产量，y1和y2分别代表在两个生产线上生产产品B的产量。

目标函数为最大化总利润，可以表示为：Maximize 3x1 + 4x2 + 2y1 + 3y2约束条件包括每个生产线的工作时间和原材料供应量：2x1 + x2 ≤82x1 + 4x2 ≤82y1 + 3y2 ≤10并且x1、x2、y1、y2都不能小于零。

通过求解这个线性规划模型，我们可以得到最优解，即在每个生产线上生产产品A和产品B的最佳产量，从而实现最大利润。

除了线性规划，运筹学还有其他分析方法，如整数规划、动态规划、网络优化等。

这些方法可以应用于不同的决策问题，解决实际的运营和管理挑战。

另一个应用案例是供应链网络优化。

供应链管理面临的一个关键问题是如何确定最优的物流网络来实现成本最小化和服务水平最大化。

运筹学可以帮助优化供应链网络的设计和运作。

【课题】5．5 线性规划问题的应用举例
【教学目标】
知识目标：用六个案例介绍了线性规划模型在生产实际中的应用.
能力目标：通过六个案例，学习线性规划模型建立的方法和技巧.
【教学重点】用适当的方法，解决线性规划问题.
【教学难点】用适当的方法，解决线性规划问题.
【教学设计】
1．本节分别介绍了投资问题，生产安排问题，环境保护问题，混合问题，运输问题和下料问题等六个案例，通过这些具体的案例，使学生认识线性规划的应用.
2．①案例1是一个投资计划制定问题，要在可承受的亏损范围内，使获利尽可能的多，因此目标函数是获得利润，约束条件是资金限制和亏损的承受范围.这是二元线性规划问题，故可用图解法解得.
②案例2是一个简单的生产安排问题，生产所获利润取决于三种产品的产量，因此以三种产品产量为决策变量，表格中列出了资源限制条件，据此可得约束条件.
③案例3是一个环境保护问题，其中各种因素已经作了简化，在列出的三个条件中，（3）成立必使（2 ）成立，因此条件有冗余，作简化后得约束条件.
④案例4是混合问题，类似于案例2.
⑤案例5是运输调配问题，这是一类典型的问题，一般的运筹学教材中都会专门介绍，本例是产销平衡的，要使总费用最低，必须知道各调运路线的运量，因此所设决策变量较多，为便于学生理解，变量写成教材的形式，有时我们也可用双下标的形式来表示变量.
⑥案例6是下料问题，与前面所举例一样，只是截法增多了.。

摘要随着我国市场经济的不断完善，同地区、不同地区、甚至跨国间的企业交易更加的频繁。

因此，在运输中如何降低运输费用、减少运输路线等问题，已经成为交易活动的重点，而随着社会分工的细化，物流和运输业不断的发展，运输问题也就变的越来越复杂，运输量有时候非常巨大，所以科学的组织运输显得十分重要。

线性规划主要应用于解决最优化问题，而运输问题可以看作是一类特殊的线性规划问题。

本文结合案例，分析了运输问题的基本特征及解决策略，并通过实例对运输问题进行了优化分析建立了线性规划的数学模型，并借助计算机进行求解，在本篇文章中主要应用的是excel求解，能快速准确的得到最优化方案，提高了实际运输工作中的经济效益。

关键词：线性规划；运输问题；excelLinear Programming In The Application Of TheTransportation Problem09404323 Li Yong Information and Computing ScienceFaculty adviser Dong Jian-xinAbstractAs the constant improvement of market economy in our country, trade become more frequently in the same areas, different regions and even multinational companies. In transit, therefore, how to reduce the transportation cost, reduce transport routes and other issues has become the focus of trading activities. With the refinement of social division of labor, the development of logistics and transport, transportation problem also becomes more and more complex, traffic sometimes very large, so the science of organization transportation appears very important. Linear programming is mainly applied to solve the optimization problem. Transportation problem can be regarded as a kind of special linear programming problem. Combining with the case, analyzes the basic characteristics of the transportation problem and solving strategy, and through the instance analysis of transportation problem is optimized, so that linear programming mathematical model is established. The solution can be obtained with the aid of computer. In this article, the problem is solved by the application of excel which can quickly and accurately get optimal solution. In addition, it also improve the economic efficiency in the actual transportation work.Key Word:Linear programming; transportation problem; excel目录引言 (2)1. 线性规划的基本理论 (2)1.1 线性规划的基本概念 (2)1.2 线性规划的一般数学模型 (3)2．线性规划在运输问题中的应用 (3)2.1 运输问题的基本特征 (3)2.2 运输问题的解决策略 (4)2.2.1 产销平衡运输问题的一般作法 (4)2.2.2 产销不平衡运输问题分两种情况 (4)3.应用excel求解运输问题简介 (5)3.1 运输问题的形式 (5)3.2 在excel中的形式 (5)3.3 excel求解步骤 (6)4.运输问题实例 (6)5.结束语 (11)6.参考文献 (12)致谢 (13)线性规划在运输问题中的应用09404323 李勇信息与计算科学指导教师董建新引言线性规划是决策系统的静态最优化数学规划方法之一。

线性规划模型及应用场景线性规划是一种运筹学中的数学方法，用于在有限的资源下寻找达到最佳目标的方案。

线性规划模型是通过建立线性关系式和目标函数以确定决策变量的最优值，来求解问题。

应用线性规划模型可以在诸多领域中找到合理的应用场景。

一、生产调度与物流管理生产调度是指以资源约束为条件，在规定时间内安排、组织和运用生产资源的管理活动。

而物流管理则是通过有效的供应链管理来实现流程和原料的优化配置。

线性规划可以通过建立生产资源约束条件和目标函数，来确定合理的生产进度和物流配送计划，从而提高生产效率、降低物流成本。

举个例子，某工厂生产两种产品A和B，生产线的时间和效率是有限的，同时每个产品有不同的售价和成本。

这时可以使用线性规划模型来确定每种产品的生产数量，使得总利润最大化。

二、金融投资与资产配置金融投资是指将资金投入到各种金融市场和资产中，以期获得回报。

而资产配置则是指在不同风险水平下，按照一定的比例配置资金到各种资产上。

线性规划可以通过建立风险约束条件和目标函数，来确定最佳的资产配置组合，以实现风险和回报间的平衡。

举个例子，某投资者有一笔固定资金，可以投资于股票、债券和货币市场基金等多个金融工具。

他可以将自己的投资目标、预期收益和风险偏好建立为线性规划模型，以确定最佳的资产配置比例，从而达到理想的投资回报。

三、运输与配送运输与配送是指将物品从生产地或仓库运往销售点或用户手中的过程。

针对运输与配送的问题，线性规划可以通过建立运输路径、运输容量和运输成本等约束条件，来确定合理的物流方案，从而达到最佳的运输效益。

例如，某物流公司需要将商品从N个供应商处运输到M个销售点，每个供应商的供货量和每个销售点的需求量是已知的，同时每个运输路径的距离和费用也是已知的。

利用线性规划模型，可以确定每个运输路径上的货物运输量和运输方式，从而降低运输成本，提高物流效率。

四、人力资源管理人力资源管理是指通过合理的组织、激励和管理，利用有限的人力资源实现组织目标。

运筹学中的线性规划理论与应用线性规划是运筹学中的一种重要工具，被广泛应用于经济、管理、工程等领域。

它的核心思想是通过建立数学模型，以线性目标函数和线性约束条件为基础，以最优化为目标，找到最佳的决策方案。

在本文中，我将讨论线性规划的基本概念和理论，并介绍其在实际应用中的案例。

一、线性规划的基本概念和理论线性规划主要研究如何分配有限资源以达到最优化的利益。

在线性规划中，决策变量、目标函数和约束条件是构建数学模型的三个基本要素。

1. 决策变量决策变量是指在问题中需要做决策的变量，通常表示为一个向量。

例如，在生产计划中，决策变量可以表示为不同产品的生产数量。

2. 目标函数目标函数是指在线性规划中需要最大化或最小化的目标指标。

目标函数通常是由决策变量线性组合而成的。

3. 约束条件约束条件是指在线性规划中限制决策变量取值范围的条件。

约束条件通常是由一系列线性不等式或等式组成的。

在线性规划问题中，通过将目标函数和约束条件转化为数学表达式，可以建立一个数学模型。

这个模型可以通过一系列数学方法求解，以达到最优化的目标。

二、线性规划在实际应用中的案例线性规划在现代管理和决策中有着广泛的应用。

以下是几个典型的案例。

1. 生产计划在生产计划中，线性规划可以用于确定不同产品的生产数量，以最大化利润或满足市场需求。

2. 配送问题在物流配送中，线性规划可以用于合理安排不同配送点的货物数量和时间，以最小化配送成本。

3. 投资组合在金融领域，线性规划可以用于确定不同投资项目的投资比例，以最大化收益或降低风险。

4. 网络流问题在网络建设中，线性规划可以用于确定网络中各节点之间的流量分配，以最大化网络传输效率。

这些案例只是线性规划在实际应用中的冰山一角。

在现代运筹学和管理科学中，线性规划以其简单、有效和灵活的特点，成为了决策分析的重要工具。

总结：线性规划是运筹学中的一种重要工具，通过建立数学模型，以线性目标函数和约束条件为基础，以最优化为目标，解决实际决策问题。

运筹学线性规划案例线性规划是运筹学中的一个重要分支，它主要研究如何利用数学模型来解决最优化问题。

在实际应用中，线性规划可以帮助企业做出最佳的决策，使资源得到最大化利用。

本文将通过一个实际案例来介绍线性规划的应用，以便读者更好地理解和掌握这一方法。

假设某公司生产两种产品A和B，它们分别需要机器加工和人工装配。

公司拥有的机器和人工资源分别为每周80小时和60人天。

产品A每单位需要机器加工2小时，人工装配3人天；产品B每单位需要机器加工3小时，人工装配2人天。

每单位产品A的利润为2000元，产品B的利润为3000元。

现在的问题是，如何安排生产计划，才能使得利润最大化呢？首先，我们可以将该问题建立成数学模型。

假设x1和x2分别表示生产产品A 和B的单位数，则该问题可以表示为：Max Z=2000x1+3000x2。

约束条件为：2x1+3x2≤80。

3x1+2x2≤60。

x1≥0，x2≥0。

接下来，我们可以通过线性规划的方法来求解最优解。

在这里，我们不妨使用单纯形法来进行求解。

首先，我们将约束条件转化成标准形式，得到：2x1+3x2+s1=80。

3x1+2x2+s2=60。

x1≥0，x2≥0。

然后，我们构造初始单纯形表，并进行单纯形法的迭代计算。

最终得到最优解为x1=20，x2=10，此时利润最大为80000元。

通过这个简单的案例，我们可以看到线性规划在实际中的应用。

通过建立数学模型和运用线性规划方法，我们可以很好地解决类似的最优化问题，使得资源得到最大化利用，从而帮助企业做出更加科学合理的决策。

总之，线性规划作为运筹学中的重要方法，具有广泛的应用前景。

通过不断地学习和实践，我们可以更好地掌握线性规划的原理和方法，为实际问题的解决提供更加科学的支持。

希望本文的案例能够帮助读者更好地理解线性规划的应用，从而在实际工作中能够更好地运用这一方法，取得更好的效果。

线性规划算法的应用案例线性规划是应用最广泛的数学优化方法之一，也是一种非常有效的运筹学技术。

它的基本思想是将问题建模成一组线性方程和线性不等式的组合，通过寻找最优解来实现目标最大化或最小化。

线性规划算法广泛应用于制造业、金融、物流和交通等领域，以下将介绍几个重要的应用案例。

1. 生产计划和调度线性规划算法可以用于制造业的生产计划和调度。

例如，在一家造纸厂中，有若干个可用的生产线、仓库和运输车辆，需要考虑原材料的成本、工人的人工费用、工厂的能耗费用以及运输的成本等因素，制定出最佳的生产计划和调度方案。

对于这类问题，可以将目标函数设置为生产成本最小化或产出效率最大化，约束条件包括原材料的库存量、生产线的容量和物流的时间窗口等。

通过使用线性规划算法，可以得到最佳的生产计划和调度方案，使得企业的生产效率和盈利能力得到提升。

2. 市场营销和广告投放线性规划算法可以帮助企业制定最佳的市场营销和广告投放方案。

例如，在一家快递公司中，需要制定如何调整价格策略、开拓市场份额、投放广告等方案，以达到最大化利润或最小化成本的目标。

对于这类问题，可以将目标函数设置为销售额最大化或成本最小化，约束条件包括市场份额的限制、广告投放预算的限制等。

通过使用线性规划算法，可以得到最佳的市场营销和广告投放方案，提高企业的营销效率和市场竞争力。

3. 交通运输和物流配送线性规划算法可以用于交通运输和物流配送领域。

例如，在一个物流中心中，需要规划配送路线和运输车辆的分配，以最小化交通堵塞和物流成本的影响。

对于这类问题，可以将目标函数设置为运输成本最小化或配送效率最大化，约束条件包括车辆数量的限制、货物配送时间的限制等。

通过使用线性规划算法，可以得到最佳的路线规划和车辆分配方案，提高企业的配送效率和物流运转效率。

4. 金融投资和风险管理线性规划算法可以用于金融投资和风险管理领域。

例如，在一个投资银行中，需要制定最佳的投资组合和股票交易策略，以最大化收益和降低风险。

线性规划在企业管理中的应用摘要：随着运筹学广泛应用，作为其一重要分支的线性规划在企业的生产管理中起到了极其重要的作用。

本文分别对线性规划和企业管理简单介绍，然后着重讨论线性规划在现代企业生产管理中的应用，并应用几种常见的解法对所提出的问题加以解答，从而获得最优解或制定最佳方案等。

关键词：线性规划企业管理数学建模线性求解Linear Programming Be Used In Business ManagementAbstract：With the Operational Research has been widly used. As the major branch,The Linear Programming paly an important role in Business Management. Thisdissertation main introduce the Linear Programming and Business Management, thenwe will discuss the apply of Linear Programming in modem Business Managemen, and use some usual methods to solve this problems which we foundand applied, so that wecan gain the optimal solution or work out optimal schema.Keywords：Linear Programming，Business Managemen ，Mathematical Modelling，Deprecatory ，Apply由于计算机技术的发展，许多利用运筹学处理的问题可在较短的时间内得出结果，线性规划作为运筹学的一重要分支，它的应用也日益广泛，如利用其数学方法，通过计算机软件应用于生产组织、几乎与管理中。

线性规划经典例题引言概述：线性规划是一种运筹学方法，用于解决线性约束条件下的最优化问题。

它在各个领域都有广泛的应用，包括生产计划、资源分配、运输问题等。

本文将介绍几个经典的线性规划例题，以帮助读者更好地理解和应用线性规划方法。

一、生产计划问题1.1 最大利润问题在生产计划中，一个常见的线性规划问题是最大利润问题。

假设一个公司有多个产品，每个产品的生产和销售都有一定的成本和利润。

我们需要确定每个产品的生产数量，以最大化整体利润。

1.2 生产能力限制另一个常见的问题是生产能力限制。

公司的生产能力可能受到设备、人力资源或原材料等方面的限制。

我们需要在这些限制下，确定每个产品的生产数量，以实现最大化的利润。

1.3 市场需求满足除了考虑利润和生产能力，还需要考虑市场需求。

公司需要根据市场需求确定每个产品的生产数量，以满足市场需求，并在此基础上最大化利润。

二、资源分配问题2.1 资金分配问题在资源分配中，一个常见的线性规划问题是资金分配问题。

假设一个公司有多个项目，每个项目需要一定的资金投入，并有相应的回报。

我们需要确定每个项目的资金分配比例，以最大化整体回报。

2.2 人力资源分配另一个常见的问题是人力资源分配。

公司的人力资源可能有限，而各个项目对人力资源的需求也不同。

我们需要在人力资源有限的情况下，确定每个项目的人力资源分配比例，以实现最大化的效益。

2.3 时间分配除了资金和人力资源，时间也是一种有限资源。

在资源分配中，我们需要合理安排时间，以满足各个项目的需求，并在此基础上实现最大化的效益。

三、运输问题3.1 最小成本运输问题在运输领域，线性规划可以用于解决最小成本运输问题。

假设有多个供应地和多个需求地，每个供应地和需求地之间的运输成本不同。

我们需要确定每个供应地和需求地之间的货物运输量，以实现最小化的总运输成本。

3.2 运输能力限制另一个常见的问题是运输能力限制。

运输公司的运输能力可能受到车辆数量、运输距离或运输时间等方面的限制。