多配对样本的非参数检验
- 格式:doc
- 大小:11.00 KB
- 文档页数:1

三对三样本差异检验方法1. 三对三样本差异检验方法是一种用于比较三组配对样本之间是否存在显著差异的统计方法。
2. 该方法适用于三组配对样本之间存在明显的关联关系,例如同一组受试者在不同时间点或条件下的观测数据。
3. 在进行三对三样本差异检验时,首先需要收集三组配对样本的数据,确保每一组的样本大小相等。
4. 接下来,将每一组的配对样本逐对进行配对差值的计算,得到每一组的差异值。
5. 然后,可以使用多种统计方法来分析三组差异值之间的差异,常见的方法包括偏差校正的t检验、方差分析(ANOVA)和非参数方法等。
6. t检验方法是一种常用的差异检验方法,适用于正态分布且方差相等的数据。
通过计算差异值的均值和标准差,来判断三组之间的差异是否显著。
7. 方差分析(ANOVA)方法是一种用于比较多个样本之间差异的方法,可以扩展到三个或更多个组别之间的比较。
8. ANOVA方法通过计算组间差异和组内差异来判断整体差异是否显著。
通常使用F统计量来进行判断,通过设置显著性水平来进行拒绝或接受原假设。
9. 非参数方法是一种用于处理非正态分布数据的方法,常见的非参数方法包括Mann-Whitney U检验、Kruskal-Wallis H检验等。
10. Mann-Whitney U检验是一种用于比较两组样本之间差异的非参数方法,将配对差异值按照大小排序,比较两组之间的秩和来判断差异是否显著。
11. Kruskal-Wallis H检验是一种用于比较三个或更多个组别之间差异的非参数方法,将配对差异值按照大小排序,通过计算秩和来判断整体差异是否显著。
12. 除了上述方法外,还可以使用回归分析、混合效应模型等多种统计方法来进行三对三样本差异的分析。
13. 三对三样本差异检验的结果通常会给出差异值的平均差异、标准差、p值等指标。
p值小于预设的显著性水平(通常为0.05)则差异被认为是显著的。
14. 在进行差异检验时,需要注意样本的选取和配对的合理性,避免选择性偏倚和配对效应的影响。

两组非参数检验方法非参数统计方法是指对总体分布形式不作任何假设的一类统计检验方法。
相对于参数统计方法而言,非参数统计方法在总体参数未知或者总体分布不满足特定假设条件的情况下更能适用。
本文将介绍两组常用的非参数检验方法:符号检验和Wilcoxon秩和检验。
第一组非参数检验方法是符号检验。
符号检验是对两个独立样本进行的一种非参数假设检验方法。
它的基本原理是比较两个样本中大于(或小于)某个特定值的样本数量是否具有显著差异。
首先,我们需要定义一个零假设(H0)和一个备择假设(H1)。
然后,计算两个样本对应数据的差值。
对于差值为正的样本,给予“+”符号;对于差值为负的样本,给予“-”符号;对于差值为零的样本,可以省略不计。
最后,通过比较“+”和“-”符号的数量,使用二项分布来计算出p值。
第二组非参数检验方法是Wilcoxon秩和检验。
这是一种用于比较两个相关样本的非参数假设检验方法。
它的思想是先将两个样本进行相互配对,然后对两个样本的差异值按大小进行排列,并赋予秩次。
然后,计算出正向差异和负向差异的秩和,并取较小值作为检验统计量。
最后,根据理论分布进行显著性检验,得到p值。
这两组非参数检验方法都有自己的适用范围和优势。
符号检验适用于样本容量较小、样本分布不满足正态分布假设的情况下,对两个独立样本差异进行显著性检验。
Wilcoxon秩和检验适用于比较两个相关样本之间的差异,如前后两次测量、配对样本的差异等。
与参数检验方法相比,这两个非参数方法更加鲁棒,能够在总体分布未知或偏离正态分布的情况下给出可靠的结果。
总结起来,非参数检验方法是一类不依赖与总体参数分布假设的统计方法,常用于小样本或总体分布不明确的情况下。
符号检验和Wilcoxon秩和检验是其中两组常用的方法。
符号检验适用于比较两个独立样本的差异,通过比较“+”和“-”符号的数量来判断差异的显著性;Wilcoxon秩和检验适用于比较两个相关样本的差异,通过对差异值按大小排列,并计算秩和来判断差异的显著性。
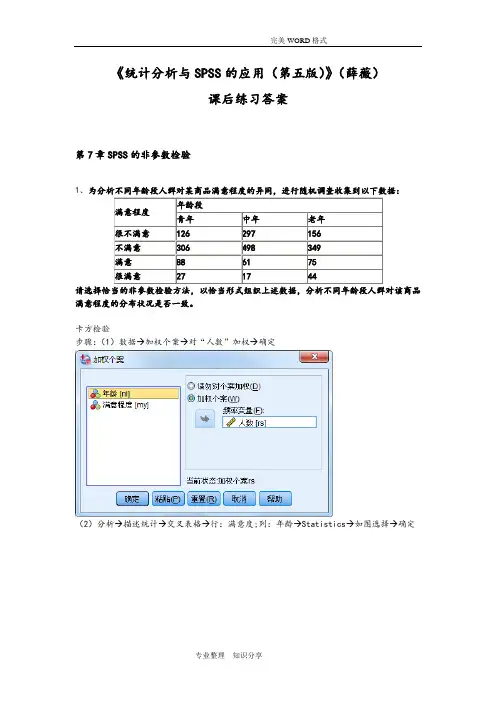
《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第7章SPSS的非参数检验1、为分析不同年龄段人群对某商品满意程度的异同,进行随机调查收集到以下数据:满意程度年龄段青年中年老年很不满意126 297 156不满意306 498 349满意88 61 75很满意27 17 44请选择恰当的非参数检验方法,以恰当形式组织上述数据,分析不同年龄段人群对该商品满意程度的分布状况是否一致。
卡方检验步骤:(1)数据→加权个案→对“人数”加权→确定(2)分析→描述统计→交叉表格→行:满意度;列:年龄→Statistics→如图选择→确定满意程度 * 年龄交叉表计数年龄总计青年中年老年满意程度很不满意126 297 156 579 不满意306 498 349 1153满意88 61 75 224很满意27 17 44 88 总计547 873 624 2044卡方检验值自由度渐近显著性(双向)皮尔逊卡方66.990a 6 .000似然比(L) 68.150 6 .000线性关联.008 1 .930McNemar-Bowker 检验. . .b有效个案数2044a. 0 个单元格 (0.0%) 具有的预期计数少于 5。
最小预期计数为 23.55。
b. 仅为 PxP 表格计算(其中 P 必须大于 1)。
因概率P值小于显著性水平(0.05),拒绝原假设,不同年龄度对该商品满意程度不一致。
2、利用第2章第7题数据,选择恰当的非参数检验方法,分析本次存款金额的总体分布与正态分布是否存在显著差异。
分析→非参数检验→旧对话框→1-样本-K—S…→选择相关项:本次存款金额[A5] →确定结果如下:单样本 Kolmogorov-Smirnov 检验本次存款金额数字282正态参数a,b平均值4738.09标准偏差10945.569最极端差分绝对.333正.292负-.333检验统计.333渐近显著性(双尾).000ca. 检验分布是正态分布。

两配对样本非参数检验在统计学中,非参数检验是一种用于比较两个或多个独立样本之间差异的方法,它不依赖于数据的分布假设。
相比之下,参数检验需要对数据的分布做出假设,例如正态分布。
非参数检验的优点是更加灵活,在不确定数据的分布情况下更能有效地进行统计推断。
以下将介绍两种常见的非参数检验方法:Wilcoxon秩和检验和Mann-Whitney U检验。
Wilcoxon秩和检验又称为Wilcoxon符号秩检验、Wilcoxon配对差异检验等,它用于比较两个配对样本的差异。
该检验的原假设是,在两个配对样本中,两两配对的差异具有相同的分布。
而备择假设是两个配对样本之间存在差异。
Wilcoxon秩和检验的步骤如下:1.给出两个配对样本,分别记作X和Y。
2.对所有配对差异进行排序,并为每个差异分配一个秩次,然后计算秩和W+和W-。
3.根据秩和W+和W-的大小,查找对应的临界值。
4.比较秩和W+和W-与临界值,如果大于等于临界值,则拒绝原假设,否则接受原假设。
Mann-Whitney U检验用于比较两个独立样本的差异,它的原假设是两个样本来自同一个总体,而备择假设是两个样本来自不同的总体。
Mann-Whitney U检验的步骤如下:1.给出两个独立样本,分别记作X和Y。
2.对两个样本的所有观测值进行排列,并为每个观测值计算秩次。
3.根据秩次,计算U值。
4.利用U值和样本量的关系,查找对应的临界值。
5.比较U值与临界值,如果小于等于临界值,则拒绝原假设,否则接受原假设。
需要注意的是,在使用非参数检验时,样本量越大,结果的准确性越高。
此外,当样本量较小时,非参数检验的效果可能会受到影响,建议使用参数检验。
综上所述,非参数检验是一种灵活、无需分布假设的统计推断方法,其中Wilcoxon秩和检验和Mann-Whitney U检验用于比较两个独立样本或配对样本之间的差异。
它们的应用范围广泛,并在实际问题中得到广泛应用。

r语言3组非参数检验非参数检验在统计学中是一种重要的方法,用于比较两组或多组数据是否具有显著性差异。
在R语言中,我们可以使用多种非参数检验方法来处理三组数据。
下面我们将介绍三种常用的非参数检验方法:卡方检验、配对卡方检验和Fisher确切概率法。
一、卡方检验卡方检验是一种用于比较两个或多个样本率或构成比是否显著的统计方法。
在R语言中,我们可以使用`chisq.test()`函数来进行卡方检验。
对于三组数据,我们可以将每两组的数据进行比较。
首先,我们需要将三组数据分别存储在三个向量中,例如:`group1`、`group2`和`group3`。
然后,我们可以使用以下代码进行卡方检验:```r#导入R语言自带的数据集data(mtcars)#将三组数据分别存储在向量中group1<-mtcars$mpggroup2<-mtcars$hpgroup3<-mtcars$drat#进行卡方检验chisq.test(cbind(group1,group2,group3))```上述代码将输出每组数据之间的卡方统计量和对应的p值。
如果p值小于预设的显著性水平(通常为0.05),则我们可以拒绝原假设,认为两组数据之间存在显著差异。
二、配对卡方检验配对卡方检验是一种用于比较两个配对样本是否具有相似性的统计方法。
在R语言中,我们可以使用`paired.test()`函数来进行配对卡方检验。
对于三组数据,我们可以将每两组的数据进行配对比较。
首先,我们需要将每两组的数据配对存储在一个矩阵或数据框中,例如:`df`。
然后,我们可以使用以下代码进行配对卡方检验:```r#创建示例数据框df<-data.frame(group1=c(1,2,3,4),group2=c(5,6,7,8),group3=c(9,10,11,12))#进行配对卡方检验paired.test(df)```上述代码将输出每组数据的配对样本之间的卡方统计量和对应的p值。


多样本尺度参数的非参数检验在统计学中,尺度参数是描述数据分布形状和范围的统计量。
常见的尺度参数包括标准差、方差和范围等。
非参数检验是一种统计推断方法,它不依赖于数据的分布形式,而是依赖于数据的排序和顺序。
多样本尺度参数的非参数检验是指在多个样本之间进行尺度参数的比较和检验,而不需要对数据的分布形式进行假设。
多样本尺度参数的非参数检验可以用于比较多个数据集的变异程度,检验它们之间是否存在显著差异。
在医学研究中,可以用多样本尺度参数的非参数检验来比较不同治疗组之间的疗效差异;在生态学研究中,可以用多样本尺度参数的非参数检验来比较不同生境条件下的物种多样性差异等。
在进行多样本尺度参数的非参数检验时,需要先对数据进行排序,然后采用适当的统计方法进行检验。
常见的多样本尺度参数的非参数检验方法包括Kruskal-Wallis检验、Friedman检验和Page趋势检验等。
下面将分别介绍这些方法的原理和应用。
Kruskal-Wallis检验是一种用于比较三个以上独立样本的尺度参数的非参数检验方法。
它是基于秩和统计量的一种拓展,用于检验多个样本之间是否存在显著差异。
Kruskal-Wallis检验的原假设是所有样本的总体分布相同,备择假设是至少有一对样本的总体分布不同。
在进行Kruskal-Wallis检验时,首先需要计算每个样本的秩和,然后用秩和统计量进行检验。
Page趋势检验是一种用于比较三个以上有序样本的尺度参数的非参数检验方法。
它是用于检验有序样本之间是否存在趋势的方法,例如时间序列数据或者剂量-响应数据。
Page趋势检验的原假设是有序样本之间不存在趋势,备择假设是有序样本之间存在趋势。
在进行Page趋势检验时,需要首先对有序样本进行秩次转换,然后再计算秩和统计量进行检验。
除了上述介绍的三种常见的多样本尺度参数的非参数检验方法,还有一些其他方法也可以用于比较多个样本之间的尺度参数差异,例如Mood检验、median检验等。

SPSSAU教程08:⾮参数检验指标解读⾮参数检验⽤于研究定类数据与定量数据之间的关系情况,是指不考虑总体的参数和总体分布类型,利⽤样本数据的总体分布形态或分布位置进⾏推断的检验⽅法。
⾮参数检验可分为:单样本的⾮参数检验、两独⽴样本的⾮参数检验、多独⽴样本的⾮参数检验、两配对样本的⾮参数检验、多配对样本的⾮参数检验。
本⽂就从多种⾮参数检验⽅法中选择⼏种常见⽅法进⾏介绍。
单样本⾮参数检验单样本Wilcoxon检验⽤于检验数据是否与某数字有明显的区别,⽐如⼿机尺⼨是否明显不等于6英⼨。
从功能上讲,单样本Wilcoxon检验与单样本T检验完全⼀致;⼆者的区别在于数据是否正态分布,如果数据正态分布,则使⽤单样本T检验,反之则使⽤单样本Wilcoxon检验。
SPSSAU-单样本Wilcoxcon分析界⾯▌分析步骤:第⼀:分析每个分析项是否呈现出显著性(P值⼩于0.05或0.01);第⼆:如果呈现出显著性;具体对⽐中位数⼤⼩,描述具体差异所在;第三:对分析进⾏总结。
▌结果解读:表1:单样本Willcoxon分析结果指标解读从上表可以看出,数据不会表现出显著性(统计量=1.481,P=0.139>0.05);意味着⼿机尺⼨并不会明显的偏离数字6,同时⼿机尺⼨的中位数为6,进⼀步说明⼿机尺⼨确实是6英⼨,从⽽证明⽣产设备正常没有问题。
独⽴样本的⾮参数检验分析两组或多组独⽴样本数据,判断数据之间的关系情况。
⽐如研究不同性别⼈群购买意愿差异情况如何或者不同城市⼉童⾝⾼差异情况⽐较等。
根据X组别的数量不同,需选择的不同的检验⽅法,如果X为两组,⽐如性别,则应使⽤MannWhitney统计量,超过两组,则使⽤Kruskal-Wallis统计量结果。
▌分析步骤:第⼀:分析X与Y之间是否呈现出显著性(P值⼩于0.05或0.01);第⼆:如果呈现出显著性;通过具体对⽐中位数⼤⼩,描述具体差异情况;第三:对分析进⾏总结。


非参数统计检验及其运用毕业论文非参数统计检验是统计学中的一种方法,它与参数检验有所不同。
参数检验通常假设数据符合某种特定的分布,如正态分布或泊松分布,然后使用参数估计和假设检验来分析数据。
而非参数检验不依赖于数据符合特定的分布,而是通过描述数据的分布情况来进行统计推断。
这种方法对于数据不符合特定分布,或者分布不确定的情况特别有用。
在毕业论文中,非参数统计检验可以应用于以下方面:1.独立样本检验:独立样本检验用于比较两组独立的样本数据,判断它们是否来自同一分布。
这种方法不需要假设数据符合特定的分布,而是通过计算两组数据的秩(即数据在排序中的位置)来进行比较。
独立样本检验可以用于解决诸如“这两组数据的平均值是否有显著差异”之类的问题。
2.配对样本检验:配对样本检验用于比较同一组数据中的两个相关变量。
这种方法也不需要假设数据符合特定的分布,而是通过计算两个变量之间的Spearman或Kendall等级相关系数来进行相关性检验。
配对样本检验可以用于解决诸如“这两个变量是否有显著相关性”之类的问题。
3.游程检验:游程检验用于检验一个随机过程是否符合平稳性。
这种方法通过计算一系列观察值的差异(即游程),然后根据这些差异的分布来判断过程是否平稳。
游程检验可以用于解决诸如“这个随机过程是否稳定”之类的问题。
4.核密度估计:核密度估计用于估计一个随机变量的概率密度函数。
这种方法通过使用核函数来平滑数据,并根据核函数的形状来估计概率密度函数的形状。
核密度估计可以用于解决诸如“这个随机变量的概率密度函数是什么形状”之类的问题。
在应用非参数统计检验时,需要注意以下几点:1.非参数统计检验通常比参数检验更加灵活和强大,但它们也需要更多的数据来进行推断。
因此,在数据量较小的情况下,参数检验可能是更好的选择。
2.非参数统计检验通常对数据的异常值更加敏感。
因此,在应用非参数统计检验之前,应该对数据进行清理和预处理,以减少异常值对结果的影响。
friedman秩和检验原理
Friedman检验,也被称为Friedman双向秩方差分析,是一种用于多个配对样本的非参数检验方法。
其原理假设是多个配对样本来自的多个总体分布无显著差异。
Friedman检验的基本步骤如下:
将每个样本在各个组别中的观察值按照从小到大的顺序进行排序,并赋予相应的秩次。
如果有相同的观察值,则平分秩次。
计算各个组别的平均秩次,即将每个组别中的所有样本的秩次相加,然后除以样本数。
计算Friedman统计量,该统计量反映了各个组别的平均秩次之间的差异。
计算Friedman检验的P值,该值表示观察到的数据与原假设之间的差异程度。
如果P值小于给定的显著性水平(通常为0.05),则拒绝原假设,认为各个组别的分布存在显著差异。
总之,Friedman检验是一种利用秩实现对多个总体分布是否存在显著差异的非参数检验方法。
通过比较各个组别的平均秩次,可以判断多个配对样本来自的多个总体的分布是否存在显著差异。
多样本比较方差分析与非参数方法的公式整理方差分析是一种常用的统计方法,用于比较多个样本之间的平均值差异。
在实际应用中,我们常常需要比较多个样本的方差,以确定它们之间是否存在显著的差异。
本文将介绍多样本比较方差分析的公式整理,并对非参数方法进行概述。
一、多样本比较方差分析多样本比较方差分析是一种常用的统计方法,用于比较多个样本的方差是否存在显著差异。
通常情况下,我们希望通过方差分析来确定样本所属的总体是否有明显的差异。
方差分析的基本假设是各组样本都来自于具有相同方差的总体,也就是说,样本之间的差异只是由于随机误差引起的。
我们可以使用方差分析来检验各组均值之间是否存在显著差异,进而判断它们所属的总体是否有明显不同。
多样本比较方差分析的公式如下所示:H0:各组均值之间没有显著差异H1:各组均值之间存在显著差异计算公式为:F = (SSB / (m-1)) / (SSE / (n-m))其中,SSB表示因组别引起的平方和,m表示组别的个数;SSE表示由于误差引起的平方和,n表示总样本数。
二、非参数方法除了上述介绍的多样本比较方差分析,还存在一种非参数方法,用于比较多个样本的位置参数差异。
与方差分析不同,非参数方法对于数据的分布不作要求,更加灵活。
下面列举一些常用的非参数方法:1. Mann-Whitney U检验Mann-Whitney U检验是一种用于比较两个独立样本的非参数方法。
它的基本思想是将两个样本的所有观测值进行合并,然后对合并后的观测值进行排序,并计算两个样本的秩和。
通过比较秩和的大小,可以得出两个样本的位置差异是否显著。
2. Kruskal-Wallis H检验Kruskal-Wallis H检验是一种用于比较多个独立样本的非参数方法。
它的基本思想是将所有样本的观测值进行合并,然后对合并后的观测值进行排序,并计算各组的秩和。
通过比较秩和的大小,可以得出各组样本的位置差异是否显著。
3. Friedman检验Friedman检验是一种用于比较多个相关样本的非参数方法。
抽样检验方案的类型有哪些抽样检验方案的类型有哪些摘要:抽样检验是统计学中常用的一种方法,用于判断一个总体是否具有某种特征。
在实际应用中,根据研究目的和数据特点的不同,可以选择不同类型的抽样检验方案。
本文将介绍六种常见的抽样检验方案类型:单样本检验、双样本检验、配对样本检验、方差分析、相关分析和非参数检验,并对每种类型的方案进行详细的叙述和讨论。
关键词:抽样检验,类型,单样本检验,双样本检验,配对样本检验,方差分析,相关分析,非参数检验一、单样本检验单样本检验是指在抽样过程中,只有一个样本参与检验的方法。
它适用于总体参数已知的情况下,通过对样本数据进行统计推断,判断总体是否满足某种特征。
常用的单样本检验方法包括:单样本均值检验、单样本比例检验和单样本方差检验。
单样本检验的步骤包括:建立假设、选择显著性水平、计算统计量和判断决策。
二、双样本检验双样本检验是指在抽样过程中,同时有两个样本参与检验的方法。
它适用于对比两个总体是否相同或不同的情况。
双样本检验常用的方法包括:独立样本 t 检验、配对样本 t 检验和 Mann-Whitney U 检验。
独立样本 t 检验适用于两个独立样本的均值比较,配对样本 t 检验适用于两个相关样本的均值比较,Mann-Whitney U 检验适用于两个独立样本的中位数比较。
三、配对样本检验配对样本检验是指在抽样过程中,每个样本中的观测值之间存在相关关系的方法。
它适用于在相同样本上进行两次观测,比较观测值前后的差异是否显著。
常用的配对样本检验方法包括:配对样本 t 检验和符号检验。
配对样本 t 检验适用于样本差异服从正态分布的情况,符号检验适用于样本差异不服从正态分布的情况。
四、方差分析方差分析是一种用于比较两个以上样本均值是否存在显著差异的方法。
它适用于多个不同总体均值之间的比较。
方差分析常用的方法包括:单因素方差分析和多因素方差分析。
单因素方差分析用于比较一个因素下不同水平之间的均值差异,多因素方差分析用于比较多个因素的交互作用对均值的影响。
课程名称实用统计软件实验项目名称多配对样本非参数检验实验成绩指导老师(签名)日期2011-12-6一.实验目的1,掌握多配对样本的非参数检验基本原理和算法;2,能够用SPSS软件解决多配对样本的非参数检验的问题。
二. 实验内容与要求1.实验内容1.书上的三个研究问题的实现。
2.书上练习与思考题第10-3题。
(提示:录入数据进行kendall协同系数检验时要把数据进行转置,读物作为变量,评论家作为行)3.为了比较A、B、C、D、E 5种药物注射后产生的皮肤疱疹的大小,选取6只家兔并给每只家兔先后分别按随机排列的次序注射这5种药物。
实验结果如下表(疱疹面积的度量单位为mm2):(提示:录入数据是也要注意,家兔在行,药物在列作为检验变量)2.实验要求:作业中要出现检验过程。
如本ppt第8页、第20页、第30页的表格及统计计算过程。
注意:今天的三种方法所处理的实际问题类型有所不同,需要根据具体问题选择不同的检验方法。
三.实验步骤具体操作参见课件多配对样本非参数检验.PPT(ftp://10.66.28.22:22)四. 实验结果(数据与图形)与分析1.书上的三个研究问题的实现。
2.书上练习与思考题第10-3题。
(提示:录入数据进行kendall协同系数检验时要把数据进行转置,读物作为变量,评论家作为行)得到卡方统计量为9.782,W系统系数为0.466,小于1,相伴概率为0.201,大于显著性水平0.05,所以评分标准不够一致。
3.为了比较A、B、C、D、E 5种药物注射后产生的皮肤疱疹的大小,选取6只家兔并给每只家兔先后分别按随机排列的次序注射这5种药物。
实验结果如下表(疱疹面积的度(提示:录入数据是也要注意,家兔在行,药物在列作为检验变量)得到卡方统计量为14.609,W系统系数为0.609,小于1,相伴概率为0.006,小于显著性水平0.05,所以皮肤疱疹大小无差异。
多配对样本的非参数检验
多配对样本的非参数检验室通过分析多组配对样本数据,推断样本来自的多个总体的中位数或分布是否存在显著差异。
例如手机乘客对多家航空公司是否满意的数据,分析航空公司的服务水平是否存在差异等等。
多配对样本的Friedman检验
多配对样本的Fiedman检验是利用秩实现对多个总体分布是否存在显著差异的非参数检验方法,其零假设是多个配对样本来自的总体的分布无显著差异。
(思想见参考书)
多配对样本的Cochran Q检验
多配对样本的Cochran Q检验通过对多个配对样本的分析,推断样本来自的多个总体的分布是否存在显著差异,其零假设是多个配对样本来自的多个总体的分布无显著差异。
(思想见参考书)
多配对样本的Kendall协同系数检验
多配对样本的Kendall协同系数检验也是一种多配对样本的非参数检验方法,与Friedman 检验方法相结合,可方便地实现对评判者的评判标准是否一致的分析。
其零假设是评判者的评判标准不一致。
(思想见参考书)。