平方差公式在因式分解中的五种表现(1)
- 格式:doc
- 大小:58.00 KB
- 文档页数:4

平方差与差平方公式及其应用在数学中,平方差与差平方公式是一种常见的数学公式,它们在代数运算、方程求解以及几何推导等方面都有广泛的应用。
本文将介绍平方差与差平方公式的定义、推导过程以及一些实际应用。
一、平方差公式平方差公式是指两个数的平方差可以展开为两个数的和与差的乘积。
设有两个数a和b,那么它们的平方差可以表示为:(a + b)(a - b)这个公式可以通过展开式来证明。
展开(a + b)(a - b)得到:a^2 - ab + ab - b^2可以看到,中间的两项-ab和ab相互抵消,最终结果为a^2 - b^2。
这就是平方差公式的推导过程。
平方差公式在代数运算中有着广泛的应用。
例如,在因式分解中,我们经常需要将一个二次多项式进行因式分解,而平方差公式可以帮助我们将其转化为两个一次多项式的乘积。
另外,在解方程的过程中,平方差公式也能够帮助我们简化计算,从而更快地得到解的结果。
二、差平方公式差平方公式与平方差公式相反,它表示两个数的差的平方可以展开为两个数的和与差的乘积。
设有两个数a和b,那么它们的差的平方可以表示为:(a - b)(a - b)同样地,我们可以通过展开式来证明这个公式。
展开(a - b)(a - b)得到:a^2 - ab - ab + b^2可以看到,中间的两项-ab和-ab相互抵消,最终结果为a^2 - 2ab + b^2。
这就是差平方公式的推导过程。
差平方公式同样在代数运算中有着广泛的应用。
它可以帮助我们进行因式分解,将一个二次多项式转化为两个一次多项式的乘积。
此外,在几何推导中,差平方公式也常常被用来计算距离、边长等问题。
三、应用举例下面我们通过一些具体的例子来展示平方差与差平方公式的应用。
例1:求解方程考虑方程x^2 - 5x + 6 = 0,我们可以使用平方差公式来求解。
将方程转化为(x - 2)(x - 3) = 0,得到x = 2或x = 3。
通过平方差公式,我们可以快速得到方程的解。





![平方差公式因式分解[下学期]北师大版(2019)](https://uimg.taocdn.com/e6fb6e5d581b6bd97f19ea63.webp)

因式分解 基础知识 总结一、 因式分解的意义1. 定义:把一个多项式化成几个整式的积的形式,叫做把这个多项式因式分解,也叫做把这个多项式分解因式。
2. 因式分解与整式乘法的区别、联系:区别:整式乘法是把几个整式相乘,化成一个多项式;因式分解是把一个多项式化成几个因式的积的形式。
联系:因式分解与整式乘法是互逆的过程。
3.公因式及其结构:公因式:一个多项式的各项都含有的因式叫做这个多项式的公因式。
公因式的结构:多项式的公因式由系数和字母部分两部分组成,系数取各项系数的最大公因数,字母取各项都含有的字母,指数取相同字母的最低次幂。
可简记为:“系数大,字母同,指数低”。
二、 因式分解的方法(一) 提公因式法1.定义:如果一个多项式的各项含有公因式,可以把这个公因式提到括号外面,将多项式写成因式乘积的形式,这种变形叫做提公因式法。
2.步骤:(1)确定公因式,(2)提公因式并确定另一个因式,原多项式除以公因式所得商就是另一个因式。
3.常用的恒等变形:223344();()();()();()()......y x x y y x x y y x x y y x x y -=---=--=---=-(二)运用公式法1.定义:如果把乘法公式反过来用,就可以把某些多项式分解因式,这种分解因式的方法叫做运用公式法。
2.因式分解公式:(1)平方差公式:22()()a b a b a b -=+-(2)完全平方公式:2222222()2()a ab b a b a ab b a b ++=+-+=-3. 2()()()x a b x ab x a x b +++=++三、因式分解的一般步骤:可以概括为“一提,二套,三分组,四检查”:“一提”:如果多项式的各项有公因式,那么先提公因式。
“二套”:如果多项式的各项没有公因式,那么可尝试套用公式法分解。
“三分组”:对于四项以上的多项式(在没有公因式后),应考虑用分组分解法。
“四检查”:检查每个因式是否还能继续分解因式,因式分解必须进行到每一个因式都不能再分解为止。

14.3.2 因式分解公式法(第一课时)一、内容和内容解析1.内容因式分解平方差公式2.内容解析本节课是在学习了提公因式法后,公式法因式分解的第一课时,它是整式乘法中平方差公式的逆向应用,在教材中处于重要的地位。
平方差公式因式分解要充分理解公式的含义,掌握公式的形式与特点. 公式左边的多项式形式上是二项式,且两项符号相反;公式左边的每一项都可以化成某一个数或式的平方形式。
基于以上分析,确定本节课的教学重点:运用平方差公式分解因式。
二、目标和目标解析1、目标(1)进一步理解因式分解的概念,体会因式分解在简化计算上的应用。
(2)会用平方差公式进行因式分解,并从中体验“整体”的思路,树立“换元”的意识。
2、目标解析达成目标(1)的标志是:学生能说出因式分解中平方差公式的特点。
知道这里的平方差公式与整式乘法中的平方差公式是互逆变形的关系。
达成目标(2)的标志是:学生在数学活动过程中,体会平方差公式的结构、特征及公式中字母的广泛含义,理解平方差公式的意义,掌握运用平方差公式解决问题的方法.并在练习中,对发生的错误做具体分析,加深对公式的理解。
三、教学问题诊断分析虽然有了第一节提公因式法做基础,但学生有时还会出现因式分解后又反转回去做乘法的错误,解决此问题的关键是让学生正确认识因式分解的概念,理解它与整式乘法的互逆变形关系。
学生在运用平方差公式分解因式的过程中经常遇到的困难是找不准哪个数或式相当于公式中的a , b 。
因此,教学中引导学生分析公式的结构特征,并运用变式训练揭示公式的本质特征,以加深学生对公式的理解.本节课的教学难点是:灵活运用平方差公式分解因式,并理解因式分解的要求。
四、教学过程设计1.复习引入问题1 你能叙述多项式因式分解的定义吗?提公因式法的定义是什么?因式分解:(1)3mx-6nx 2;(2)4a 2b+10ab-2ab 3;(3)252 y 师生活动:学生独立思考并解答,找同学的答案投影展示。

因式分解公式法因式分解是数学中一项重要的基础概念和运算技巧之一,广泛运用于各个领域的数学问题解决中。
因式分解公式法(一)是指根据不同的因式形式来进行分解,通过寻找公式来简化和改写一元多项式的表示形式。
本文将详细介绍因式分解公式法(一)的原理和应用方法。
一、原理根据因式分解公式法(一),我们将一元多项式表示为两个因子的乘积形式,其中一个因子通常是一个特殊的多项式形式或者常数。
通过这种形式,我们可以更容易地对多项式进行化简、提取公因子、寻找根以及解决相关的问题。
二、应用方法1.完全平方公式完全平方公式是因式分解公式法(一)中一种常见的应用方法。
当多项式具有形如x^2 + 2ax + a^2或者x^2 - 2ax + a^2的形式时,我们可以将其分解为(x + a)^2或者(x - a)^2例如,对于多项式x^2+6x+9,我们可以将其根据完全平方公式分解为(x+3)^2、同样地,对于多项式x^2-8x+16,我们可以分解为(x-4)^22.平方差公式平方差公式是因式分解公式法(一)中另一种常见的应用方法。
当多项式具有形如x^2-a^2的形式时,我们可以将其分解为(x+a)(x-a)。
例如,对于多项式x^2-16,我们可以根据平方差公式得到(x+4)(x-4)。
3.a^3±b^3的因式分解当多项式具有形如a^3±b^3的形式时,我们可以利用立方和差公式进行因式分解。
立方和差公式的表达式如下:a^3 ± b^3 = (a ± b)(a^2 ∓ ab + b^2)例如,对于多项式x^3+8,我们可以利用立方和差公式分解为(x+2)(x^2-2x+4)。
同样地,对于多项式x^3-27,我们可以分解为(x-3)(x^2+3x+9)。
4.完全立方公式完全立方公式是因式分解公式法(一)中又一种常见的应用方法。
当多项式具有形如a^3 ± 3a^2b + 3ab^2 ± b^3的形式时,我们可以将其分解为(a ± b)^3例如,对于多项式x^3+3x^2+3x+1,我们可以根据完全立方公式分解为(x+1)^35.其他应用除了上述常见的应用方法,因式分解公式法(一)还可以应用于其他情况。
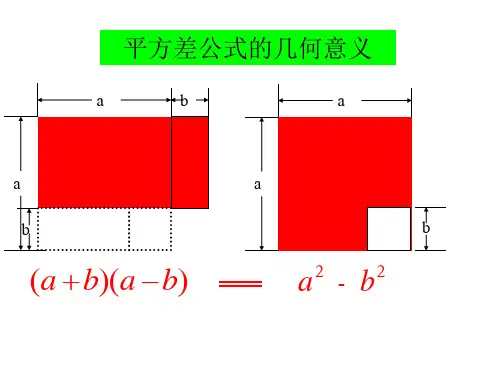
平方差公式在因式分解中的五种表现
应用平方差公式,把多项式进行分解因式的方法,就叫做平方差公式法。
公式表述为:
a2- b2=(a+b)(a-b)。
应用平方差公式满足的条件:
等式的左边是一个两项多项式,并且构成这个多项式的两个单项式之间是作减法运算;
等式的右边一个因式是等式左边两个平方幂的底数的和,另一个因式是等式左边两个平方幂的底数的差。
1直接应用
例1、分解因式:24
x-=.(2008年贵阳市)
分析:左边是两个单项式的差,关键是把数字4写成22,这样,左边就变形为x2- 22,这样,就和公式一致了。
解::x2-4=x2- 22=(x+2)(x-2)。
2、提后用公式
例2、分解因式:3x2-27= .(08茂名)
分析:在分解因式时,先考虑提公因式,后考虑用平方差公式法。
解:
3x2-27
=3(x2-9)
=3(x2- 32)
=3(x+3)(x-3)。
3、变化指数后用公式
例3、248-1能被60和70之间的两个数整除。
这两个数各是多少?
分析
因为,48=2×24,所以,248=(22)24=(224)2,这样,就满足了平方差公式的要求了。
解:
因为,48=2×24,所以,248=(22)24=(224)2,
所以,248-1=(224)2-(1)2=(224+1)(224-1)
=(224+1)(224-1)=(224+1)【(212)2-(1)2】
=(224+1)【(212+1)(212-1)】
=(224+1)(212+1)【(26)2-(1)2】
=(224+1)(212+1)【(26+1)(26-1)】
=(224+1)(212+1)(26+1)【(23)2-(1)2】
=(224+1)(212+1)(26+1)【(23+1)(23-1)】
=(224+1)(212+1)(26+1)×9×7
=(224+1)(212+1)(26+1)×65×63
因为,整除的两个数在60和70之间,
且60<63<70,60<65<70,
所以,这两个数分别是63、65。
4、先局部用完全平方公式,后整体用平方差公式
例4、若a、b、c是三角形的三条边长,则代数式,a2-2ab- c2+b2的值:
A、大于零
B、小于零
C、等于零
D、与零的大小无关
分析:
由a 2-2ab- c 2+ b 2= (a-b )2- c 2=(a-b+c )(a-b-c ),
因为、a 、b 、c 是三角形的三条边长,
所以,两边之和一定是大于第三边的,因此,a+c >b ,b+c >a ,
所以,a-b+c >0,a-b-c <0,
所以,(a-b+c )(a-b-c )<0,
因此,正确的答案是B 。
5、乒乓球比赛中的应用
例5、有10为乒乓球选手进行乒乓球单循环比赛(每两人之间均要赛一场)如果用x 1,y 1顺次表示第一号选手胜与负的场数,用x 2,y 2顺次表示第二号选手胜与负的场数,
用x 10,y 10顺次表示第十号选手胜与负的场数,则这10位选手胜的场数的平方和与他们负的场数的平方和是相等的。
即2102221x x x +++ =2102221y y y ++ 。
你能用所学的知识解释里面的道理吗? 分析:
因为,是进行的单循环比赛,
所以,每一位选手的胜的场数与负的场数是相同的,都是9场,
从比赛的整体来看,所有队员胜的场数与负的场数也一定是相等的, 这两个隐含的条件是问题解决的关键所在。
解:
因为,是进行的单循环比赛,
所以,911=+y x ,。