matlab的平面二维图的绘制

matlab中plot用法在MATLAB中，plot函数用于绘制二维图形。

它可以绘制折线图、散点图、柱状图等等，非常常用。

下面是plot函数的一些基本用法和参数的解释。

基本用法：plot函数的最基本用法是传入一个向量作为参数，这个向量中的每个数值对应于图中的一个点，将会在某轴上按顺序绘制。

例如：某=[1,2,3,4,5];%某轴上的坐标y=[1,4,9,16,25];%y轴上的坐标plot(某, y); % 绘制折线图此时将会绘制出一个连接了(1,1)、(2,4)、(3,9)、(4,16)、(5,25)这五个点的折线。

可以通过使用线条样式和颜色来定制绘图。

例如：plot(某, y, 'r--'); % 使用红色的虚线绘制折线图更多的线条样式和颜色选项可以参考MATLAB文档。

plot函数的参数：除了上述的基本用法外，plot函数还有其他可选参数，用来定制绘图的外观和行为。

1. 标记样式：可以通过在plot函数的线条样式后面加上一个标记样式来在每个点处绘制标记。

plot(某, y, 'r-o'); % 在每个点处绘制红色实线和圆形标记2. 坐标轴范围：可以用a某is函数来设置坐标轴的范围，例如：title('My Plot');某label('某-a某is');ylabel('y-a某is');4. 图例：可以通过legend函数添加一个图例，用于解释图中的各个线条所代表的内容。

legend('Plot 1', 'Plot 2');5. 多个图形在同一个图中：可以通过hold函数来设置是否在同一个图中绘制多个图形。

hold on;plot(某, y1);plot(某, y2);hold off;这是plot函数的一些基本用法和参数的解释。

在实际应用中，plot函数有很多其他的选项和用法，可以根据具体需求进行查阅MATLAB文档，深入学习和了解。

matlab中plot函数的用法在MATLAB中，plot函数用于绘制二维图形。

它可以用于创建线图、散点图、条形图等多种类型的图表。

该函数的基本语法是：plot(x, y)plot(x, y, LineSpec)plot(y)plot(x1, y1, LineSpec1, x2, y2, LineSpec2, ...)其中,-x表示要绘制的数据点的x坐标，可以是一个向量或矩阵；-y则表示相应的y坐标，也可以是一个向量或矩阵；- LineSpec 是一个可选参数，表示绘制线条的样式，如颜色、线型、标记等。

以下是plot函数的几种常见用法：1.绘制线图可以通过传递 x 和 y 向量来实现线图的绘制。

例如，要绘制一个sin函数的图像，可以执行以下代码：x = 0:0.1:2*pi;y = sin(x);plot(x, y)这将绘制一个从0到2π范围内的sin曲线。

2.绘制散点图除了绘制线图，plot函数还可以用于绘制散点图，只需将参数LineSpec 设置为空即可。

例如，要绘制一组随机生成的散点，可以执行以下代码：x = rand(1, 100);y = rand(1, 100);plot(x, y, '.') % '.'表示绘制散点图这将在坐标系中生成100个随机散点。

3.自定义线条样式可以通过传递 LineSpec 参数来自定义线条的样式。

它由颜色、线型和标记三部分组成。

例如，要绘制红色的虚线曲线，可以执行以下代码：x = 0:0.1:2*pi;y = sin(x);plot(x, y, 'r--')其中，'r'表示红色，'--'表示虚线。

4.多图绘制plot函数还支持多图绘制，即在同一个图形窗口绘制多个图形。

只需将多组 x 和 y 数据传递给plot函数即可。

例如，要在同一个图形窗口中绘制两个曲线，可以执行以下代码：x1 = 0:0.1:2*pi;y1 = sin(x1);x2 = 0:0.1:2*pi;y2 = cos(x2);plot(x1, y1, 'r', x2, y2, 'b')这将分别绘制sin函数和cos函数的图像，其中sin函数用红色表示，cos函数用蓝色表示。

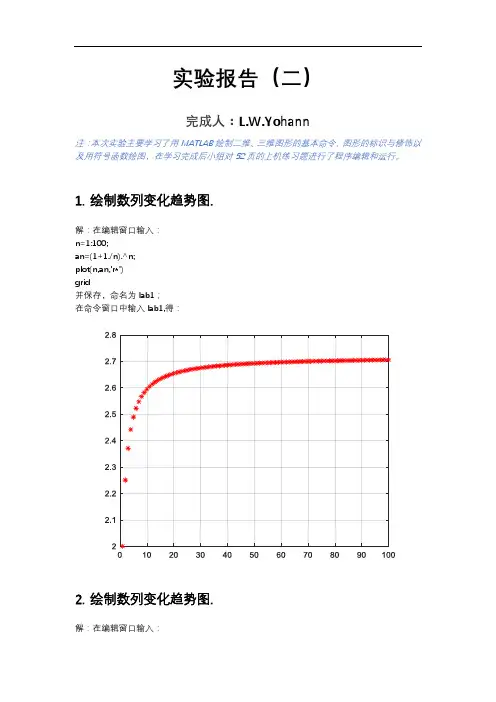
实验报告（二）完成人：L.W.Yohann注：本次实验主要学习了用MATLAB绘制二维、三维图形的基本命令、图形的标识与修饰以及用符号函数绘图，在学习完成后小组对52页的上机练习题进行了程序编辑和运行。

1.绘制数列变化趋势图.解：在编辑窗口输入：n=1:100;an=(1+1./n).^n;plot(n,an,'r*')grid并保存，命名为lab1；在命令窗口中输入lab1,得：2.绘制数列变化趋势图.解：在编辑窗口输入：n=1:0.1:50;an=n.^(1./n);plot(n,an,'r*')grid并保存，命名为lab2；在命令窗口中输入lab2,得：3.绘制函数在无定义点处的变化趋势.解：在编辑窗口输入：x=-10:0.05:10;y=sin(x)./x;plot(x,y,'r*')grid并保存，命名为lab3；在命令窗口中输入lab3,得：4.在同一坐标系中画出函数及其Taylor多项式的图像解：y=sinx在编辑窗口输入：syms xf=sin(x);T6=taylor(f,x);T8=taylor(f,x,'Order',8);T10=taylor(f,x,'Order',10);T12=taylor(f,x,'Order',12);fplot([T6 T8 T10 T12 f])xlim([-8 8])grid onlegend('approximation of sin(x) up to O(x^6)',...'approximation of sin(x) up to O(x^8)',...'approximation of sin(x) up to O(x^{10})',...'approximation of sin(x) up to O(x^{12})',...'sin(x)','Location','Best')title('Taylor Series Expansion')并保存，命名为lab4sin；在命令窗口中输入lab4sin,得：y=exp(x)在编辑窗口输入：syms xf=exp(x);T6=taylor(f,x);T8=taylor(f,x,'Order',8);T10=taylor(f,x,'Order',10);T12=taylor(f,x,'Order',12);fplot([T6 T8 T10 T12 f])xlim([-8 8])grid onlegend('approximation of exp(x) up to o(x^6)',...'approximation of exp(x) up to o(x^8)',...'approximation of exp(x) up to o(x^{10})',...'approximation of exp(x) up to o(x^{12})',...'exp(x)','Location','Best')title('Taylor Series Expansion')并保存，命名为lab4exp；在命令窗口中输入lab4exp,得：5.符号函数绘图.注：在matlab r2010b 和matlab r2019b中对绘制函数图像的输入方法有不同的要求，故此类题分两个版本来求解。

MATLAB绘图与图形处理人们很难从一大堆原始的数据中发现它们的含义，而数据图形恰能使视觉感官直接感受到数据的许多内在本质，发现数据的内在联系。

MATLAB可以表达出数据的二维，三维，甚至四维的图形。

通过图形的线型，立面，色彩，光线，视角等属性的控制，可把数据的内在特征表现得淋漓尽致。

下面我们分别介绍图形的命令。

7.1 二维图形7.1.1 基本平面图形命令命令1 plot功能线性二维图。

在线条多于一条时，若用户没有指定使用颜色，则plot循环使用由当前坐标轴颜色顺序属性（current axes ColorOrder property）定义的颜色，以区别不同的线条。

在用完上述属性值后，plot又循环使用由坐标轴线型顺序属性（axes LineStyleOrder property）定义的线型，以区别不同的线条。

用法plot(X,Y) 当X,Y均为实数向量，且为同维向量（可以不是同型向量），X=[x(i)]，Y=[y(i)]，则plot(X,Y)先描出点(x(i)，y(i))，然后用直线依次相连；若X，Y为复数向量，则不考虑虚数部分。

若X，Y均为同维同型实数矩阵，X = [X(i)]，Y = [Y(i)]，其中X(i),Y(i)为列向量，则plot(X,Y)依次画出plot(X(i),Y(i))，矩阵有几列就有几条线；若X，Y中一个为向量，另一个为矩阵，且向量的维数等于矩阵的行数或者列数，则矩阵按向量的方向分解成几个向量，再与向量配对分别画出，矩阵可分解成几个向量就有几条线；在上述的几种使用形式中，若有复数出现，则复数的虚数部分将不被考虑。

plot(Y) 若Y为实数向量，Y的维数为m，则plot(Y)等价于plot(X,Y)，其中x=1：m；若y 为实数矩阵，则把y按列的方向分解成几个列向量，而y 的行数为n，则plot(Y)等价于plot(X,Y)其中x=[1;2;…;n]；在上述的几种使用形式中，若有复数出现，则复数的虚数部分将不被考虑。

matlab中plot函数的用法在MATLAB中，plot函数是用来绘制二维图形的最基本函数之一、它可以用于绘制多种类型的图形，如折线图、散点图、柱状图等。

plot函数的基本语法是：plot(x, y)其中，x是一个向量，表示x轴上的数据点的位置；y是一个向量，表示y轴上的数据点的位置。

x和y的长度必须相同。

下面我们将详细介绍plot函数的各种用法。

1.绘制折线图：最常见的用法是绘制折线图，即根据给定的x和y值，绘制一条连接这些点的连续线段。

例如：x=[0:0.1:10];y = sin(x);plot(x, y)在上面的例子中，x为一个从0到10的向量，间隔为0.1；y为对应于x的正弦值。

plot函数会自动绘制出这些点，并连接起来，生成折线图。

2.绘制散点图：如果只想显示数据点，而不需要连线，可以使用散点图的形式。

例如：x=[12345];y=[42351];plot(x, y, 'o')上面的例子中，x和y分别表示x轴和y轴上的数据点的位置。

'o'表示使用圆点标记数据点。

3.修改线条样式：可以通过参数来修改绘制的线条样式。

例如：x=[0:0.1:10];y = sin(x);plot(x, y, '-', 'LineWidth', 2)上面的例子中，'-'表示绘制的线条为实线，'LineWidth'指定线条的宽度为2个单位。

4.绘制多条曲线：可以通过在plot函数中多次调用x和y值，来绘制多条曲线。

例如：x=[0:0.1:10];y1 = sin(x);y2 = cos(x);plot(x, y1, x, y2)上面的例子中，绘制了两条曲线，y1为sin函数的曲线，y2为cos函数的曲线。

5.添加图例：可以通过legend函数来添加图例，以便区分不同的曲线。

例如：x=[0:0.1:10];y1 = sin(x);y2 = cos(x);plot(x, y1, x, y2)legend('sin', 'cos')上面的例子中，添加了两个图例，分别对应y1和y2的曲线。

plot2在matlab中的用法MATLAB是一种功能强大的数值计算与科学可视化软件，常用于工程、科学和数学领域的开发和研究。

其中的plot2函数是用于绘制二维图形的工具之一，并提供了许多灵活的用法。

一、plot2函数的基本语法在MATLAB中，plot2函数的基本语法如下：plot2(x,y)其中，x和y是行向量，表示需要绘制的数据点的x坐标和y坐标。

二、绘制简单的二维折线图首先，我们来看一个简单的例子，使用plot2函数绘制一个二维折线图：matlabx = 1:10;y = x.^2;plot2(x,y)在以上代码中，我们定义了x从1到10的行向量，y为x的平方。

然后，通过plot2函数绘制了这些数据点，得到了一个折线图。

三、绘制多个数据集的折线图plot2函数还可以用于同时绘制多个数据集的折线图。

我们可以通过为每个数据集传入不同的x和y来实现这一点，如下所示：matlabx1 = 1:10;y1 = x1.^2;x2 = 1:10;y2 = x2.^3;x3 = 1:10;y3 = x3.^4;plot2(x1,y1,x2,y2,x3,y3)在以上代码中，我们定义了三组数据集，分别为x1和y1、x2和y2、x3和y3。

然后，通过将这些数据集传入plot2函数中，就可以同时绘制这些数据集的折线图。

四、自定义折线图的样式plot2函数还具有很多可调整的参数，使我们能够自定义折线图的样式。

下面是一些常用的参数和示例用法：1. 颜色：可以通过'-'或''来设置折线的样式，如下所示：matlabplot2(x,y,'r-')在以上代码中，我们使用红色的实线来表示折线。

matlabplot2(x,y,'b')在以上代码中，我们使用蓝色的虚线来表示折线。

2. 线宽：可以通过'LineWidth'参数来设置折线的线宽，如下所示：matlabplot2(x,y,'b-','LineWidth',2)在以上代码中，我们设置折线的线宽为2个单位。

matlab中plot的作用
Matlab中的plot函数是用于绘制二维图形的重要工具，它可以将数据点连接起来形成一条曲线或折线，提供了一种直观的方式来展示数据及其关系。

下面是plot函数的详细作用：
1. 绘制二维图形：plot函数可以根据给定的数据点，在二维平面上绘制出相应的曲线或折线图。

用户可以通过调整坐标轴范围、颜色、线型等参数，使得图像更加美观和易于理解。

2. 可视化数据：通过plot函数，用户可以将数据可视化，以便更好地理解和分析数据。

例如，用户可以通过对不同颜色和标记符号进行设置，将不同类型的数据点区分开来。

3. 分析数据：通过对plot函数生成的图像进行分析，用户可以了解到数据之间存在的关系和趋势。

例如，在一条曲线中出现的峰值可能表示某些特殊事件发生的时间或位置。

4. 与其他Matlab函数结合使用：plot函数还可以与其他Matlab函数结合使用，例如legend、xlabel、ylabel等。

这些函数可以为图像添加标题、标签和注释等信息，从而使得图像更加具有可读性和可理解性。

5. 保存图像：在生成了满意的二维图形后，用户还可以使用Matlab 提供的保存图像函数，将图像保存为各种格式的文件，例如png、jpg 等。

这些文件可以用于后续的分析和展示。

总之，plot函数是Matlab中非常重要的二维图形绘制工具，它可以帮助用户可视化数据、分析数据、与其他函数结合使用，并且可以方便地保存图像。

matlab中最根本的函数plot（）的用法之五兆芳芳创作标签： matlab plot 指令5.1 二维平面图形5.1.1 根本图形函数plot 是绘制二维图形的最根本函数，它是针对向量或矩阵的列来绘制曲线的.也就是说，使用plot 函数之前，必须首先定义好曲线上每一点的x 及y 坐标，经常使用格局为：（1）plot(x) 当x 为一向量时，以x 元素的值为纵坐标，x 的序号为横坐标值绘制曲线.当x 为一实矩阵时，则以其序号为横坐标，按列绘制每列元素值相对于其序号的曲线，当x 为m× n 矩阵时，就由n 条曲线.（2）plot(x,y) 以x 元素为横坐标值，y 元素为纵坐标值绘制曲线.（3）plot(x,y1,x,y2,…) 以公共的x 元素为横坐标值，以y1,y2,… 元素为纵坐标值绘制多条曲线.例5.1.1 画出一条正弦曲线和一条余弦曲线.>> x=0:pi/10:2*pi;>> y1=sin(x);>> y2=cos(x);>> plot(x,y1,x,y2)图5.1.1 函数plot 绘制的正弦曲线在绘制曲线图形时，经常采取多种颜色或线型来区分不合的数据组，MATLAB 软件专门提供了这方面的参数选项（见表 5.1.1），我们只要在每个坐标后加上相关字符串，就可实现它们的功效.- 2 -表5.1.1 画图参数表色彩字符颜色线型字符线型格局标识表记标帜符号数据点形式标识表记标帜符号数据点形式y 黄- 实线. 点< 小于号m 紫：点线o 圆s 正方形c 青-. 点划线x 叉号d 菱形r 红- - 虚线+ 加号h 六角星g 绿* 星号p 五角星b 蓝v 向下三角形w 白^ 向上三角形k 黑> 大于号例如，在上例中输入>> plot(x,y1,'r+-',x,y2,'k*:')图5.1.2 使用不合标识表记标帜的plot 函数绘制的正弦曲线5.1.2 图形修饰MATLAB 软件为用户提供了一些特殊的图形函数，用于修饰已经绘制好的图形.函数寄义grid on (/off) 给当前图形标识表记标帜添加（取消）网络xlable(‘string’) 标识表记标帜横坐标ylabel(‘string’) 标识表记标帜纵坐标title(‘string’) 给图形添加题目text(x,y,’string’) 在图形的任意位置增加说明性文本信息gtext(‘string’) 利用鼠标添加说明性文本信息axis([xmin xmax ymin ymax]) 设置坐标轴的最小最大值- 3 -例5.1.2 给例5.1.1 的图形中参加网络和标识表记标帜.（见图5.1.3 和5.1.4）>> x=0:pi/10:2*pi;>> y1=sin(x);>> y2=cos(x);>> plot(x,y1,x,y2)>> grid on>> xlabel('independent variable X')>> ylabel('Dependent Variable Y1 & Y2')>> title('Sine and Cosine Curve')>> text(1.5,0.3,'cos(x)')>> gtext('sin(x)')>> axis([0 2*pi -0.9 0.9])图5.1.3 使用了图形修饰的plot 函数绘制的正弦曲线5.1.3 图形的比较显示在一般默认的情况下，MATLAB 每次使用plot 函数进行图形绘制，将重新产生一个图形窗口.但有时希望后续的图形能够和前面所绘制的图形进行比较.一般来说有两种办法一是采取hold on(/off)命令，将新产生的图形曲线叠加到已有的图形上；二是采取subplot(m,n,k)函数，将图形窗口分隔成n m×个子图，并选择第k 个子图作为当前图形，然后在同一个视图窗口中画出多个小图形.例5.1.3 在同一窗口中绘制线段.（见图5.1.5）>> x=0:pi/10:2*pi;>> y1=sin(x);>> y2=cos(x);>> y3=x;>> y4=log(x);>> plot(x,y1,x,y2)>> hold on>> plot(x,y3)>> plot(x,y4)>> hold off例5.1.4 在多个窗口中绘制图形.（见图5.1.6）>> x=0:pi/10:2*pi;>> y1=sin(x);>> y2=cos(x);>> y3=exp(x);>> y4=log(x);>> subplot(2,2,1);>> plot(x,y1);>> subplot(2,2,2);>> plot(x,y2);>> subplot(2,2,3);>> plot(x,y3);>> subplot(2,2,4);>> plot(x,y4);[说明] （1）子窗口的序号按行由上往下，按列从左向右编号.（2）如果不必指令clf 清除，以后图形将被绘制在子图形窗口中.图5.1.4 设置坐标轴最大最小值的正弦曲线- 5 -- 6 -5.2 三维立体图形5.2.1 三维曲线图与二维图形相对应，MATLAB 提供了plot3 函数，可以在三维空间中绘制三维曲线，它的格局类似于plot，不过量了z 标的目的的数据.plot3 的调用格局为：plot3(x1,y1,z1,x2,y2,z2,...)其中x1,y1,z1,x2,y2,z2,…等辨别为维数相同的向量，辨别存储着曲线的三个坐标值，该函数的使用方法和plot 类似，也可以采取多种的颜色或线型（见表 5.1.1）来区分不合的数据组，只需在每组变量前面加上相关字符串便可实现该功效.例5.2.1 绘制方程x=ty=sin(t)z=cos(t)在t=[0,2*pi]上的空间方程.（见图5.2.1）>> clf>> x=0:pi/10:2*pi;>> y1=sin(x);>> y2=cos(x);>> plot3(y1,y2,x,'m:p')>> grid on>> xlabel('Dependent Variable Y1')>> ylabel('Dependent Variable Y2')>> zlabel('Independent Variable X')>> title('Sine and Cosine Curve')图5.2.1 函数plot 绘制的三维曲线图- 7 -5.2.2 三维曲面图如果要画一个三维的曲面，可以使用mesh(X,Y,Z)或surf(X,Y,Z)函数来实现.mesh 函数为数据点绘制网格线，图形中的每一个已知点和其邻近的点用直线连接.surf函数和mesh 的用法类似，但它可以画出着色概略图，图形中的每一个已知点与其相邻点以平面连接.为便利测试立体画图，MATLAB 提供了一个peaks 函数，它可以产生一个的高斯散布矩阵，其生成方程是N N ×z=3*(1-x).^2.*exp(-(x.^2)-(y+1).^2)-10*(x/5-x.^3-y.^5).*exp(-x.^2-y.^2)-1/3*exp(-(x+1).^2-y.^2)对应的图形是一个凹凸有致的曲面，包含了三个局部极大点及三个局部极小点.下面使用peaks 函数来比较一下mesh 和surf 的区别.例5.2.2 辨别用mesh 函数和surf 函数绘制高斯矩阵的曲面. >> z=peaks(40);>> mesh(z);>> surf(z);图5.2.2 mesh 函数绘制的三维曲面图- 8 -图5.2.3 surf 函数绘制的着色概略图在曲面画图中，另一个经常使用的函数是meshgrid 函数，其一般引用格局是：[X, Y]=meshgrid (x, y)其中x 和y 是向量，通过meshgrid 函数就可将x 和y 指定的区域转换成为矩阵X 和Y.这样我们在画图时就可以先用meshgrid 函数产生在x-y 平面上的二维的网格数据，再以一组z 轴的数据对应到这个二维的网格，便可画出三维的曲面.例5.2.3 绘制方程sin((x^2+y^2)^(1/2))z = ---------------------(x^2+y^2)^(1/2)在x∈[-7.5,7.5];y∈[-7.5,7.5] 的图形.>> x=-7.5:0.5:7.5;y=x;>> [X,Y]=meshgrid(x,y);>> R=sqrt(X.^2+Y.^2)+eps;>> Z=sin(R)./R;>> surf(X,Y,Z)>> xlabel('X 轴标的目的')>> ylabel('Y 轴标的目的')>> zlabel('Z 轴标的目的')例 5.2.4 绘制由方程形成的立体图.（见图 5.2.5）z=xe-(x^2+y^2)>> clear>> x=-2:0.1:2;y=x;>> [X,Y]=meshgrid(x,y);>> Z=X.*exp(-X.^2-Y.^2);- 9 ->> surf(X,Y,Z)- 10 -5.2.3 不雅察点MTALAB 允许用户设置不雅察点，其指令是：view(azimuth,elevation)其中方位角azimuth 是不雅察点和坐标原点连线在x-y 平面的投影和y 轴负标的目的的夹角，仰角elevation 是不雅察点与坐标原点的连线和x-y 平面的夹角.对于这两个角度，三维图形的默认值辨别是-37.5 和30，二维图形的默认值是0 和90.例5.2.5 从不合的角度不雅察高斯矩阵的曲面.>> z=peaks(40);>> subplot(2,2,1);>> mesh(z);>> subplot(2,2,2);>> mesh(z);>> view(-37.5,-30);>> subplot(2,2,3);>> mesh(z);>> view(180,0);>> subplot(2,2,4);>> mesh(z);>> view(0,90);图5.2.6 对应不合不雅察点的三维曲面图5.3 其他图形函数除了plot 画图函数以外，在有些场合对绘制的曲线会有一些特殊要求，这就要其他函数来实现，经常使用的几种函数如下（见表5.3.1）- 11 -表5.3.1 其他图形函数表函数寄义loglog 使用对数坐标系画图semilogx 横坐标为对数坐标轴，纵坐标为线性坐标轴semilogy 横坐标为线性坐标轴，纵坐标为对数坐标轴polar 绘制极坐标图fill 绘制实心图bar 绘制直方图pie 绘制饼图area 绘制面积图quiver 绘制向量场图stairs 绘制阶梯图sterm 绘制火柴杆图>> x=0:pi/10:2*pi;>> y1=sin(x);>> subplot(2,2,1);>> plot(x,y1);>> subplot(2,2,2);>> bar(x,y1);>> subplot(2,2,3);>> fill(x,y1,'g');>> subplot(2,2,4);>> stairs(x,y1,'k');图5.3.1 其他图形函数- 12 -5.3.1 直方图函数bar(x)可以绘制直方图，这对统计或数据收集很是直不雅实用.它共有四种形式：bar,bar3,barh 和bar3h，其中bar 和bar3 辨别用来绘制二维和三维竖直方图，barh 和bar3h 辨别用来绘制二维和三维水平直方图，调用格局是：bar(x,y) 其中x 必须单调递增或递减，y 为n m×矩阵，可视化结果为m 组，每组n 个垂直柱，也就是把y 的行画在一起，同一列的数据用相同的颜色暗示；bar(x,y,width) （或bar(y,width)）指定每个直方条的宽度，如width>1，则直方条会重叠，默认值为width=0.8；bar(…,’grouped’) 使同一组直方条紧紧靠在一起；bar(…,’stack’) 把同一组数据描述在一个直方条上.>> y=[5 3 2 9;4 7 2 7;1 5 7 3];>> subplot(2,2,1),bar(y)>> x=[5 9 11];>> subplot(2,2,2),bar3(x,y)>> subplot(2,2,3),bar(x,y,'grouped')>> subplot(2,2,4),bar(rand(2,3),.75,'stack')图5.3.2 直方图5.3.2 面积图函数area 用来绘制面积图，面积图在plot 的根本上填充x 轴和曲线之间的面积，该图用于查抄某个数在该列所有数的总和中所占的比例.>> x=-3:3;>> y=[3 2 5;6 1 8;7 4 9;6 3 7;8 2 9;4 2 9;3 1 7];>> area(x,y)- 13 -图5.3.3 面积图5.3.3 饼图函数pie 用来绘制饼图，它可以形象地暗示出向量中各元素所占比例.其调用格局是：pie(x) x 中的元素通过x/sum(x)进行归一化，以确定饼图中的份额；pie(x,explode) 向量explode 和x 元素数相同，用来指出需要分隔的饼片，explode 中不为零的部分会被分隔.图5.3.4 饼图- 14 -例 5.3.4 设某班的某课程的考试成绩如下：90 分以上有32 人，81 至90 有58 人，71至80 分有27 人，60 至70 分为21 人，60 分以下有16 人，画出饼图.（见图5.3.4）>> x=[32 58 27 21 16];>> explode0=[1 0 0 0 0];>> subplot(1,2,1)>> pie(x,explode0)>> explode1=[0 0 0 0 1];>> subplot(1,2,2)>> pie(x,explode1)5.3.4 不合坐标系中的画图Semilogx,semilogy,loglo,polar(theta,rho)的使用办法和plot 完全类似，不合的只是绘制到不合的图形坐标上.函数semilogx 绘制x 轴为对数标度的图形，在半对数坐标系中画图；函数semilogy 绘制y 轴为对数标度的图形；函数loglog 绘制两个轴都为对数距离的图形；函数polar(theta,rho)绘制极坐标图形，其中theta 为相角，rho 为其对应的半径.例5.3.5 绘制ρ=acos(3θ),a=2 的图形.（见图5.3.5）>> theta=-pi:pi/80:pi;>> polar(theta,2*cos(3*theta))图5.3.5 极坐标图5.4 符号表达式画图MATLAB 软件提供了将表达式进行图形显示的功效.完成此功效需调用fplot 函数和ezplot 函数.- 15 -函数fplot 用来绘制数学函数，其调用格局为：fplot(fun,lims)其中fun 就是所要绘制的函数，可以是定义函数的M 文件名，也可以是以x 为变量的可计较字符串.例如’diric(x,10)’或’[sin(x),cos(x)]’，对于向量x 的每个元素，函数fun(x)必须前往一个行向量.如果fun 前往[f1(x),f2(x),f3(x)]，输入[x1;x2]，就会前往矩阵f1(x1) f2(x1) f3(x1)f1(x2) f2(x2) f3(x2)lims=[XMIN XMAX YMIN YMAX]限定了x,y 轴上的画图空间.>> subplot(2,2,1),fplot('humps',[0 1])>> subplot(2,2,2),fplot('abs(exp(-j*x*(0:9))*ones(10,1))',[0 2*pi])>> subplot(2,2,3),fplot('[tan(x),sin(x),cos(x)]',2*pi*[-1 1 -1 1]) >> subplot(2,2,4),fplot('sin(1./x)',[0.01 0.1],1e-3)图5.4.1 fplot 函数绘制表达式图形ezplot 函数是简捷画图指令之一，它无需数据准备，直接画出函数图形，根本调用格局为ezplot(f)其中f 是字符串或代表数学函数的符号表达式，只有一个符号变量，可以是x，缺省情况下x 轴的画图区域为] 2 , 2 [ π π ? ，但我们可以用ezplot(f,xmin,xmax)或ezplot(f,[xmin,xmax])来指定x 的规模. >> y='x^2';>> subplot(1,2,1)- 16 ->> ezplot(y)>> subplot(1,2,2)>> y='sin(x)';>> ezplot(y,[-pi,pi])图5.4.2 ezplot 函数绘制表达式图形5.5 plot 函数MATLAB 对数据是按列存储和计较的，运用plot(x)时，当x 为一个向量时，以其元素为纵坐标，其序号为横坐标值绘制曲线.当x 为实矩阵时，则以其序号为横坐标，按列绘制每列元素相对于序号的曲线，当x 为n m×矩阵时，就有n 条曲线.如果x,y 是同维向量，plot(x,y)指令以x 元素为横坐标值，y 元素为纵坐标值绘制曲线.如x 是向量，y 是有一维与x 元素数量相等的矩阵，则以x 为配合横坐标，按列绘制y 每列元素值，曲线数为y 的另一维的元素数.如果x,y 是同维矩阵，则以x,y 对应列元素为、纵坐标辨别绘制曲线，数目等于矩阵的列数.>> x=[3 5 10 8];>> subplot(2,2,1)>> plot(x)>> x=[3 5 10 8;7 2 9 4;2 7 2 7]';>> subplot(2,2,2)>> plot(x)>> x=[3 5 6 8];>> y=[1 5 10 4];- 17 ->> subplot(2,2,3)>> plot(x,y)>> x=[1 3 5 7;2 4 6 8]';>> y=[6 2 5 10;3 5 2 6]';>> subplot(2,2,4)>> plot(x,y,'k:*')5.6 交互式图形指令ginput 是一个比较特殊的图形指令，用作获得图上数据，例如指令>>[x,y]=ginput(6) % 从图形上选取6 个点.此时，ginput 指令将把当前图形调入前台，同时光标变成十字叉，移动光标，使穿插点落在目标点上，单击鼠标，便可取得该点数据.>> fplot('humps',[0 1])>> ginput(6)x =- 18 -y =。

matlab 中plot函数的用法在MATLAB 中，plot 函数用于绘制二维图形，包括线图、散点图等。

以下是plot 函数的用法示例：1、基本线图：绘制简单的线图。

matlabCopy codex = 1:10;y = sin(x);plot(x, y);title('Sine Wave');xlabel('X-axis');ylabel('Y-axis');2、多条线图：绘制多条线在同一图中。

matlabCopy codex = 1:10;y1 = sin(x);y2 = cos(x);plot(x, y1, 'r', x, y2, 'b');title('Sine and Cosine Waves');legend('Sine', 'Cosine');3、散点图：绘制散点图。

matlabCopy codex = rand(1, 50);y = rand(1, 50);plot(x, y, 'o');title('Scatter Plot');xlabel('X-axis');ylabel('Y-axis');4、自定义线条样式和颜色：使用不同的线条样式和颜色。

matlabCopy codex = 0:0.1:2*pi;y1 = sin(x);y2 = cos(x);plot(x, y1, '-r', x, y2, '--b');title('Custom Line Styles and Colors');legend('Sine', 'Cosine');5、标记数据点：在线图上标记数据点。

matlabCopy codex = 1:10;y = sin(x);plot(x, y, 'o-', 'MarkerSize', 8);title('Sine Wave with Marked Data Points');xlabel('X-axis');ylabel('Y-axis');这些示例展示了plot 函数的一些常见用法。

matlab pcolor例子函数如何使用MATLAB中的pcolor函数进行数据可视化？MATLAB是一个功能强大的科学计算软件，广泛应用于各个领域的数据分析和可视化工作中。

其中，pcolor函数是MATLAB中一个常用的的数据可视化函数，可以绘制二维平面上的数据图像。

pcolor函数的基本语法为：pcolor(X,Y,C)其中，X和Y是指定数据矩阵C在x轴和y轴上的坐标点，而C则是待绘制的数据矩阵。

下面我们将一步步回答如何使用MATLAB中的pcolor函数进行数据可视化。

第一步：准备数据首先，我们需要准备要绘制的数据矩阵。

数据矩阵可以从外部文件中导入，也可以在MATLAB中生成。

假设我们有一个数据矩阵Z，其中包含了一个5x5的方阵，我们可以使用rand函数生成一个随机矩阵，代码如下：Z = rand(5);第二步：创建坐标点矩阵在使用pcolor函数绘图之前，我们需要创建与数据矩阵Z相对应的坐标点矩阵，即X和Y。

坐标点矩阵的大小应与数据矩阵相同，并且包含了每个坐标点在x轴和y轴上的坐标值。

以等间隔的方式创建坐标点矩阵X和Y，可以使用meshgrid函数，代码如下：[X,Y] = meshgrid(1:size(Z,2), 1:size(Z,1));其中，size(Z,2)和size(Z,1)分别表示Z矩阵在x轴和y轴上的维度大小。

第三步：使用pcolor函数绘图现在，我们已经准备好了数据矩阵Z和坐标点矩阵X、Y，可以使用pcolor 函数进行数据可视化了。

代码如下：pcolor(X,Y,Z);colorbar;其中，pcolor函数的前两个参数是坐标点矩阵X和Y，第三个参数是数据矩阵Z。

colorbar函数用于显示颜色对应的数值范围。

第四步：添加坐标轴标签和图例为了使可视化结果更加清晰和易于理解，我们可以添加坐标轴标签和图例。

使用xlabel和ylabel函数分别为x轴和y轴添加标签，如下所示：xlabel('X');ylabel('Y');使用title函数为图像添加一个标题，如下所示：title('Data Visualization');第五步：调整颜色映射方式pcolor函数默认使用parula颜色映射方式，可以通过colormap函数来改变颜色映射方式。